〖数学〗7.1.2 全概率公式 课件(共22张PPT)-2024-2025学年高二下学期数学人教A版(2019)选择性必修第三册
文档属性
| 名称 | 〖数学〗7.1.2 全概率公式 课件(共22张PPT)-2024-2025学年高二下学期数学人教A版(2019)选择性必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 602.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 17:28:08 | ||
图片预览







文档简介
(共22张PPT)
7.1.2 全概率公式
旧知回顾
(1)古典概型的概念及古典概型的概率公式;
(2)互斥事件概率的加法公式;
(3)条件概率公式及乘法公式;
情境引入
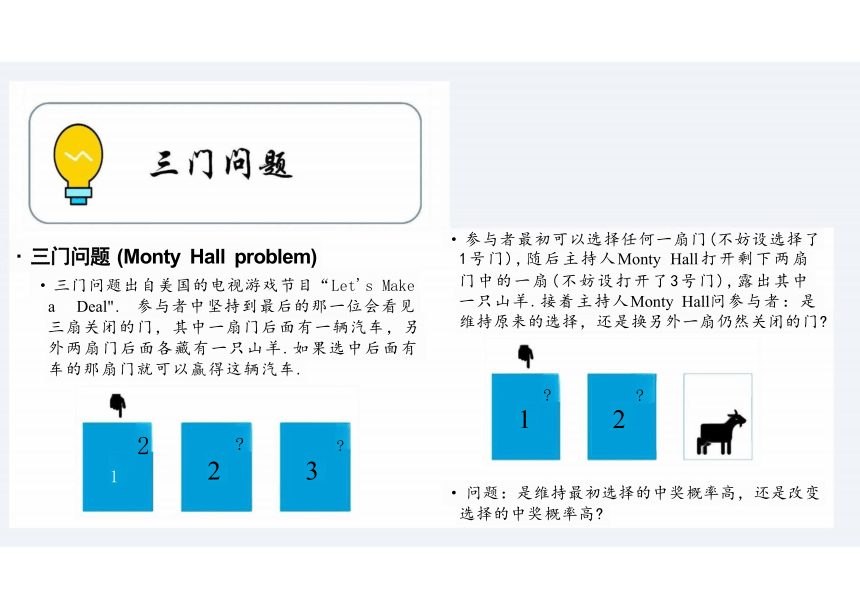
蒙提霍尔问题(三门问题)
· 三门问题 (Monty Hall problem)
· 三门问题出自美国的电视游戏节目“Let's Make a Deal". 参与者中坚持到最后的那一位会看见 三扇关闭的门,其中一扇门后面有一辆汽车,另 外两扇门后面各藏有一只山羊.如果选中后面有 车的那扇门就可以赢得这辆汽车.
· 参与者最初可以选择任何一扇门(不妨设选择了 1号门),随后主持人Monty Hall 打开剩下两扇
门中的一扇(不妨设打开了3号门),露出其中
一只山羊.接着主持人Monty Hall问参与者:是 维持原来的选择,还是换另外一扇仍然关闭的门
· 问题:是维持最初选择的中奖概率高,还是改变 选择的中奖概率高
2
1
3
2
1
2
思考1:假如你是ben, 你会怎样选择
思考2:如果改变选择,中奖的概率是多少
思考3:如果不改变选择,中奖的概率又是多少
问题引入
袋子中装有a个红球和b个蓝球,这些球除颜色外完全相同。 每次随机摸出1个球,摸出的球不再放回.
Q1: 从袋子中任取一球,求取得红球的概率
Q2: 从袋子中任取一球,求取得蓝球的概率
Q3: 从袋子中任取一球,摸出的球不再放回,求第2次取得
红球的概率是多少
Q4: 从袋子中任取一球,摸出的球不再放回, 求第2次取得 蓝球的概率是多少
Q3: 从袋子中任取一球,摸出的球不再放回,求第2次取得
红球的概率是多少
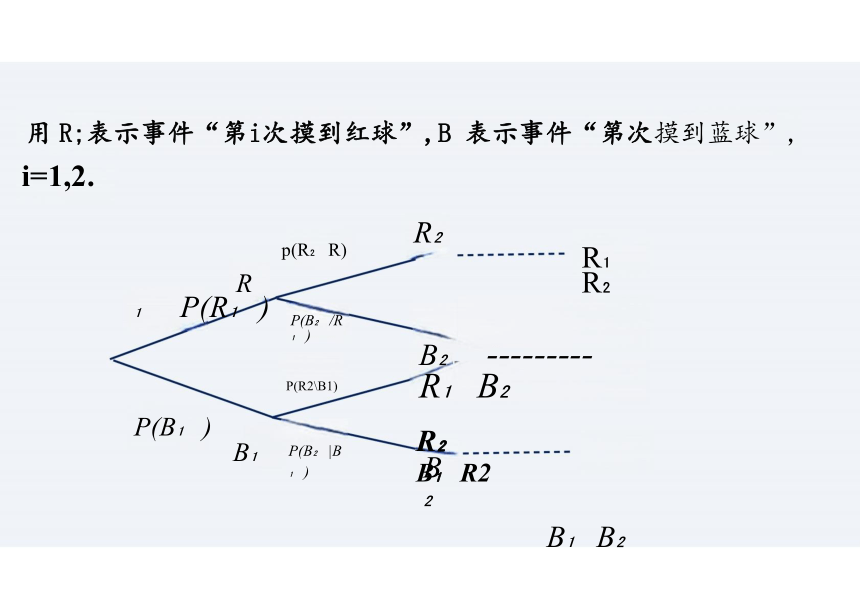
用 R;表示事件“第次摸到红球”,B 表示事件“第i次摸到蓝球”,
i=1,2.
用 R;表示事件“第i次摸到红球”,B 表示事件“第次摸到蓝球”,
i=1,2.
R
R R
B ---------R B
R B R2
B B
R P(R )
P(B )
B
p(R R)
P(B /R )
P(R2\B1)
P(B |B )
B
Q4: 从袋子中任取一球,摸出的球不再放回,求第2次取得
蓝球的概率是多少
思考4:比较分析(3)和(4),并归纳出这两个问题的共性
按照某种标准,将一个复杂事件表示为两个互斥事件的并,
再由概率的加法公式和乘法公式求得这个复杂事件的概率.
设A ,A ,…,An 是一组两两互斥的事件,A UA U….UA,=2,
且P(A;)>0,i=1,2,…,n, 则对任意的事件BSΩ, 求事件B 的概率P(B).
概念生成
概念生成
一般地,设A ,A ,…,An 是一组两两互斥的事件,
A UA U.….UA,=2, 且 P(A)>0,i=1,2,…,n, 则对任意的
称上面的公式为全概率公式。
事件BC0, 有
Q
思考5:结合古典概型和Venn图,尝试证明全概率公式
Q
思考6:总结出全概率公式求解问题的一般思路
运用全概率公式求概率的解题步骤:
(1)用符号表示随机事件:设A ,A ,…,A SΩ, 设事件B 要求:A ,A ,…,An 两两互斥,A UA U.….UA,=2,
且P(A;)>0,i=1,2,…,n,
(2)分别计算概率: p(A,)P(B|A)
(3)求概率:
例题讲解
例1 某学校有A,B 两家餐厅,王同学第1天午餐时随机地选择 一家餐厅用餐.如果第1天去A餐厅,那么第2天去A餐厅的概率为 0.6;如果第1天去B餐厅,那么第2天去A餐厅的概率为0.8,计 算王同学第2天去A餐厅用餐的概率.
例2 有3台车床加工同一型号的零件,第1台加工的次品率为6%,
第2,3台加工的次品率均为5%,加工出来的零件混放在一起. 已
知第1,2,3台车床加工的零件数分别占总数的25%,30%,45% .
(1)任取一个零件,计算它是次品的概率;
例2 有3台车床加工同一型号的零件,第1台加工的次品率为6%,
第2,3台加工的次品率均为5%,加工出来的零件混放在一起. 已知 第1,2,3台车床加工的零件数分别占总数的25%,30%,45% .
(2)如果取到的零件是次品,计算它是第i(i=1,2,3) 台车床加工 的概率.
思考7: 在上面的例题解答中,概率P(A;),P(A;|B) 的实际意
义是什么 你能梳理出解决问题(2)过程中的关键等式吗
P(A)是试验之前就已知的概率,它是第诒车床加工的零件
所占的比例,称为先验概率.当已知抽到的零件是次品 (B
发 生 ) , P(A; |B) 是这件次品来自第诒车床加工的可能性
大小,通常称为后验概率.
关键等式
贝叶斯公式: 设A ,A ,…,An 是一组两两互斥的事件,
A UA U.….UA,=2, 且 P(A;)>0,i=1,2,…,n, 则对任意的 事件BE2,P(B)>0, 有
,i=1,2,...,n.
注意:贝叶斯公式一般适用于已知事件的结果,求某一种情况
发生的概率.
三门问题
思考8:三门问题中,主持人做了什么试验 是随机事件吗
概率是多少 如何求其概率
A;表示事件“第i扇门后有汽车”,B;表示事件“主持人打开了
第i扇 门 ”
若第1扇门后有汽车,主持人只能打开2,3号门,则
若第2扇门后有汽车,主持人只能打开3号门,则
P(B A )=1
若第3扇门后有汽车,主持人只能打开2号门,则
P(B A )=0
P(B)=P(A)P(B A)+P(A)P(B A)+P(A)P(B A)=2
根据贝叶斯公式,在3号门打开的条件下,1号门和2号门后
有汽车的概率分别为
因此,改选后中奖的概率更高
课堂小结
1.全概率公式中将样本空间拆分成若干个两两互斥事件的作 用是什么
2.应用全概率公式的步骤是什么
7.1.2 全概率公式
旧知回顾
(1)古典概型的概念及古典概型的概率公式;
(2)互斥事件概率的加法公式;
(3)条件概率公式及乘法公式;
情境引入
蒙提霍尔问题(三门问题)
· 三门问题 (Monty Hall problem)
· 三门问题出自美国的电视游戏节目“Let's Make a Deal". 参与者中坚持到最后的那一位会看见 三扇关闭的门,其中一扇门后面有一辆汽车,另 外两扇门后面各藏有一只山羊.如果选中后面有 车的那扇门就可以赢得这辆汽车.
· 参与者最初可以选择任何一扇门(不妨设选择了 1号门),随后主持人Monty Hall 打开剩下两扇
门中的一扇(不妨设打开了3号门),露出其中
一只山羊.接着主持人Monty Hall问参与者:是 维持原来的选择,还是换另外一扇仍然关闭的门
· 问题:是维持最初选择的中奖概率高,还是改变 选择的中奖概率高
2
1
3
2
1
2
思考1:假如你是ben, 你会怎样选择
思考2:如果改变选择,中奖的概率是多少
思考3:如果不改变选择,中奖的概率又是多少
问题引入
袋子中装有a个红球和b个蓝球,这些球除颜色外完全相同。 每次随机摸出1个球,摸出的球不再放回.
Q1: 从袋子中任取一球,求取得红球的概率
Q2: 从袋子中任取一球,求取得蓝球的概率
Q3: 从袋子中任取一球,摸出的球不再放回,求第2次取得
红球的概率是多少
Q4: 从袋子中任取一球,摸出的球不再放回, 求第2次取得 蓝球的概率是多少
Q3: 从袋子中任取一球,摸出的球不再放回,求第2次取得
红球的概率是多少
用 R;表示事件“第次摸到红球”,B 表示事件“第i次摸到蓝球”,
i=1,2.
用 R;表示事件“第i次摸到红球”,B 表示事件“第次摸到蓝球”,
i=1,2.
R
R R
B ---------R B
R B R2
B B
R P(R )
P(B )
B
p(R R)
P(B /R )
P(R2\B1)
P(B |B )
B
Q4: 从袋子中任取一球,摸出的球不再放回,求第2次取得
蓝球的概率是多少
思考4:比较分析(3)和(4),并归纳出这两个问题的共性
按照某种标准,将一个复杂事件表示为两个互斥事件的并,
再由概率的加法公式和乘法公式求得这个复杂事件的概率.
设A ,A ,…,An 是一组两两互斥的事件,A UA U….UA,=2,
且P(A;)>0,i=1,2,…,n, 则对任意的事件BSΩ, 求事件B 的概率P(B).
概念生成
概念生成
一般地,设A ,A ,…,An 是一组两两互斥的事件,
A UA U.….UA,=2, 且 P(A)>0,i=1,2,…,n, 则对任意的
称上面的公式为全概率公式。
事件BC0, 有
Q
思考5:结合古典概型和Venn图,尝试证明全概率公式
Q
思考6:总结出全概率公式求解问题的一般思路
运用全概率公式求概率的解题步骤:
(1)用符号表示随机事件:设A ,A ,…,A SΩ, 设事件B 要求:A ,A ,…,An 两两互斥,A UA U.….UA,=2,
且P(A;)>0,i=1,2,…,n,
(2)分别计算概率: p(A,)P(B|A)
(3)求概率:
例题讲解
例1 某学校有A,B 两家餐厅,王同学第1天午餐时随机地选择 一家餐厅用餐.如果第1天去A餐厅,那么第2天去A餐厅的概率为 0.6;如果第1天去B餐厅,那么第2天去A餐厅的概率为0.8,计 算王同学第2天去A餐厅用餐的概率.
例2 有3台车床加工同一型号的零件,第1台加工的次品率为6%,
第2,3台加工的次品率均为5%,加工出来的零件混放在一起. 已
知第1,2,3台车床加工的零件数分别占总数的25%,30%,45% .
(1)任取一个零件,计算它是次品的概率;
例2 有3台车床加工同一型号的零件,第1台加工的次品率为6%,
第2,3台加工的次品率均为5%,加工出来的零件混放在一起. 已知 第1,2,3台车床加工的零件数分别占总数的25%,30%,45% .
(2)如果取到的零件是次品,计算它是第i(i=1,2,3) 台车床加工 的概率.
思考7: 在上面的例题解答中,概率P(A;),P(A;|B) 的实际意
义是什么 你能梳理出解决问题(2)过程中的关键等式吗
P(A)是试验之前就已知的概率,它是第诒车床加工的零件
所占的比例,称为先验概率.当已知抽到的零件是次品 (B
发 生 ) , P(A; |B) 是这件次品来自第诒车床加工的可能性
大小,通常称为后验概率.
关键等式
贝叶斯公式: 设A ,A ,…,An 是一组两两互斥的事件,
A UA U.….UA,=2, 且 P(A;)>0,i=1,2,…,n, 则对任意的 事件BE2,P(B)>0, 有
,i=1,2,...,n.
注意:贝叶斯公式一般适用于已知事件的结果,求某一种情况
发生的概率.
三门问题
思考8:三门问题中,主持人做了什么试验 是随机事件吗
概率是多少 如何求其概率
A;表示事件“第i扇门后有汽车”,B;表示事件“主持人打开了
第i扇 门 ”
若第1扇门后有汽车,主持人只能打开2,3号门,则
若第2扇门后有汽车,主持人只能打开3号门,则
P(B A )=1
若第3扇门后有汽车,主持人只能打开2号门,则
P(B A )=0
P(B)=P(A)P(B A)+P(A)P(B A)+P(A)P(B A)=2
根据贝叶斯公式,在3号门打开的条件下,1号门和2号门后
有汽车的概率分别为
因此,改选后中奖的概率更高
课堂小结
1.全概率公式中将样本空间拆分成若干个两两互斥事件的作 用是什么
2.应用全概率公式的步骤是什么
