〖数学〗导数的几何意义课件(共19张PPT) 2024-2025学年高二下学期数学北师大版(2019)选择性必修第二册
文档属性
| 名称 | 〖数学〗导数的几何意义课件(共19张PPT) 2024-2025学年高二下学期数学北师大版(2019)选择性必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 17:36:30 | ||
图片预览




文档简介
(共19张PPT)
A △
△△
复习引入
1.函数y=f(x) 在x=x, 处的导数
设函数y=f(x), 当自变量x从x 变到x 时,函数值y从f(xo)变到f(x ),
平均变化率趋于一个固定的值,我们称这个值为平均变化率的极限,记作
那么这个值就是函数y=f(x) 在点x 的瞬时变化率
, 也叫y=f(x )在点x 的导数。
2.求函数y=f(x) 在x=x, 处导数的步骤
(1)求函数的增量△y=f(x +△x)-f(x );
(2)求平均变化率
(3)取极限, 得导娄
新课探究
探 究 1 :我们知道,导数f(xo) 表示函数y=f(x) 在x=x 处
的瞬时变化率,反映了函数y=f(x) 在x=x 附近的变化情况.
那么导数f(x ) 的几何意义是什么
平均变化率 瞬时变化率 导数
平均变化率的几何意义 导数f'(xo) 的几何意义
它的几何意义是表示
结合直线斜率的定义可知:函数在点P
到点P 之间的平均变化率即为割线P P 的斜率.
平均变化率的几何意义
平均变化率的几何意义
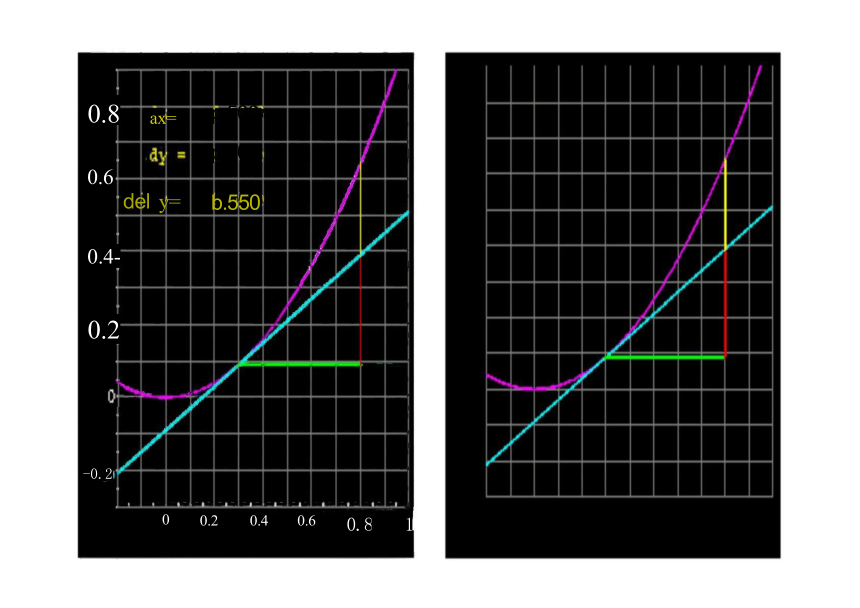
设函数y=f(x) 的图象如图,点Po(xo,f(x )), 点P(xo+△x,f(xo+△x)),
则f(x) 在[xo,xo+△x] 上的平均变化率
p.500
p.300
0.6
b.550
0.4-
0.2
-0.2
0.8 1
0.8 ax=
del y=
0.2 0.4 0.6
0
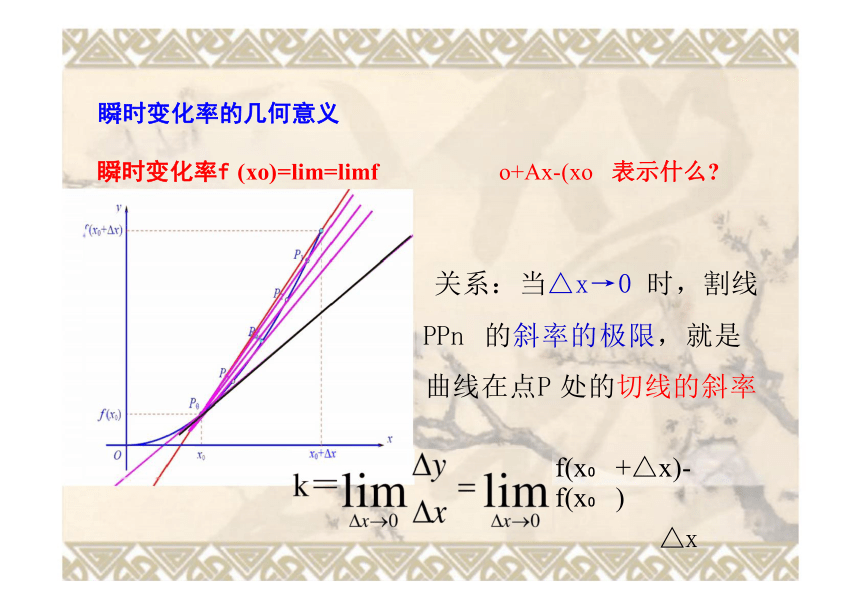
瞬时变化率的几何意义
瞬时变化率f (xo)=lim=limf o+Ax-(xo 表示什么
关系:当△x→0 时,割线
PPn 的斜率的极限,就是
曲线在点P 处的切线的斜率
f(x +△x)-f(x )
△x
新课讲授
1.切线的定义
在曲线y=f(x) 上任取一点P(x,f(x))
当点P(x,f(x))沿着曲线y=f(x) 无限趋近于点P。(xo,f(xo)
)时,割线P P无限趋近于一个确定的位置,这个确定的位置
的直线P T 称为曲线y=f(x) 在点P,处的切线.
割线P P的斜率k 切线P T的斜率k。 0
函数y=f(x) 在x=x 处的导数f(x )
曲线y=f(x) 在点P (xo,f(x )) 处切线的斜率k
2.导数的几何意义 思考3: 导 数f(x )的几何意义是什么
y
f(x +Ax)
f(x )
导数f(x ) 的几何意义
Ax
x x +Ax x
y=f(x) pl
f(x +△x)-f(x
T
=f'(x )
即kpr=tanα=f'(x )
曲线y=f(x) 在点M(x ,f(x ) 处的切线方程为
y-yo=f'(x )(x-x )
探究2:你能求出曲线y=f(x) 在点M (xo,f(xo)) 处的切线方
程是什么吗
典例精析
例1 如图1.1-3,它表
示跳水运动中高度随
时间变化的函数h(t)
=-4.9t +6.5t+10 的
图象.根据图象,请描
述、比较曲线h(t) 在t 。, 图1.1-3
t ,t 附 近 的 变 化 情 况
利用曲线在动点的切线,刻画曲线在动点附近
的变化情况.
解 我 们 用 曲 线h(x)在to,t ,t 处的切线,刻画曲
线h(t)在上述三个时刻附近的变化情况
VV
l
(1当t=to 时,曲线h(t)在
to处的切线l,平行于x轴 .
所以,在t=to 附近曲线比
较平坦,几乎没有升降
(2)当t=t 时,曲线h(t) 在 t 图1.1-3 l
处的切线l,的斜率h(t )<0. 所以,在t=t 附近曲线下 降,即函数h(t)在t=t 附近单调递减
3 当t=t 时,曲线ht) 在t 处的切线l 的斜率ht )<0.
所以,在t=t 附近曲线下降即函数h(t)在t=t, 附 近 也
单调递减
从图1.1-3可见,直线l 的倾斜程度小于直线2的倾斜
程度,这说明曲线h(t)在t附 近 比 在t 附近下降得缓慢
A
例3:曲线y=f(x)=x -1 在x=x, 处的切线与曲线
y=g(x)=1-x 在x=x,处的切线互相平行.
(1)求x 的值;(2)求曲线y=f(x) 在x=x 处的切线方程
由题意得2x =-3x , 解得x =0 或
解析:(1)
例3:曲线y=f(x)=x -1 在x=x, 处的切线与曲线
y=g(x)=1-x 在x=x, 处的切线互相平行.
(1)求x,的值;(2)求曲线y=f(x) 在x=x, 处的切线方程.
解析:(2)当x =0 时,f'(xo)=0, 又f(0)=-1,
故所求切线方程为y=-1;
A
当 时 ,
故所求切线方程
1 . 如图,直线l是曲线y=f(x) 在x=4 处的切线,则f( 4)=( )
A
1
解:根据导数的几何意义知f(4)是曲线y=f(x)在x=4 处
的切线的斜率k, 注 意 到k= , 所 以
B.3 C.4 D.5
巩固练习
2
A △
2.函数f(x)的图象如图所示,下列数值排序正确的是( A ).
(A)f'(1)>f'(2)>f'(3)>0
(B)f'(1)(C)0(D)f'(1)>f'(2)>0>f'(3)
A △
3.如图,函数y=f(x) 的图象在点P处的切线方程是y=-x+8 ,
则f(5)十f'(5)= 2 _
A
解析:点P横坐标为5,
故由在点P处切线为y=-x+8,
得f'(5)=-1,f(5)=-5+8=3.
∴f(5)+f'(5)=2.
y=-x+8
P
0 5 x
个y
4、已知函数f(x)的图象如图所示,则下列不等关系中正确的是
A.0B.0COD.0A △
f'(2) 为函数f(x)的图象在点B(2,f(2)) 处的切线的斜率,
f'(3) 为函数f(x)的图象在点A(3,f(3)) 处的切线的斜率,
根据图象可知0解析
本课小结
1.切线的定义: 设Q为曲线C上不同于点P的一点,则直线PQ称 为曲线的割线.随着点Q 沿曲线C 向点P运动,当点Q 无限逼近点 P时,直线PQ 最终成为点P处最逼近曲线的直线l, 这时直线l称 为曲线在点P处的切线.
2.导数的几何意义:
函数y=f(x)在x 处的导数f'(x ), 是曲线y=f(x)在点(x ,f(xo))
处的切线的斜率. 函数y=f(x)在x 处切线的斜率反映了导数的几
何意义.
A △
△△
复习引入
1.函数y=f(x) 在x=x, 处的导数
设函数y=f(x), 当自变量x从x 变到x 时,函数值y从f(xo)变到f(x ),
平均变化率趋于一个固定的值,我们称这个值为平均变化率的极限,记作
那么这个值就是函数y=f(x) 在点x 的瞬时变化率
, 也叫y=f(x )在点x 的导数。
2.求函数y=f(x) 在x=x, 处导数的步骤
(1)求函数的增量△y=f(x +△x)-f(x );
(2)求平均变化率
(3)取极限, 得导娄
新课探究
探 究 1 :我们知道,导数f(xo) 表示函数y=f(x) 在x=x 处
的瞬时变化率,反映了函数y=f(x) 在x=x 附近的变化情况.
那么导数f(x ) 的几何意义是什么
平均变化率 瞬时变化率 导数
平均变化率的几何意义 导数f'(xo) 的几何意义
它的几何意义是表示
结合直线斜率的定义可知:函数在点P
到点P 之间的平均变化率即为割线P P 的斜率.
平均变化率的几何意义
平均变化率的几何意义
设函数y=f(x) 的图象如图,点Po(xo,f(x )), 点P(xo+△x,f(xo+△x)),
则f(x) 在[xo,xo+△x] 上的平均变化率
p.500
p.300
0.6
b.550
0.4-
0.2
-0.2
0.8 1
0.8 ax=
del y=
0.2 0.4 0.6
0
瞬时变化率的几何意义
瞬时变化率f (xo)=lim=limf o+Ax-(xo 表示什么
关系:当△x→0 时,割线
PPn 的斜率的极限,就是
曲线在点P 处的切线的斜率
f(x +△x)-f(x )
△x
新课讲授
1.切线的定义
在曲线y=f(x) 上任取一点P(x,f(x))
当点P(x,f(x))沿着曲线y=f(x) 无限趋近于点P。(xo,f(xo)
)时,割线P P无限趋近于一个确定的位置,这个确定的位置
的直线P T 称为曲线y=f(x) 在点P,处的切线.
割线P P的斜率k 切线P T的斜率k。 0
函数y=f(x) 在x=x 处的导数f(x )
曲线y=f(x) 在点P (xo,f(x )) 处切线的斜率k
2.导数的几何意义 思考3: 导 数f(x )的几何意义是什么
y
f(x +Ax)
f(x )
导数f(x ) 的几何意义
Ax
x x +Ax x
y=f(x) pl
f(x +△x)-f(x
T
=f'(x )
即kpr=tanα=f'(x )
曲线y=f(x) 在点M(x ,f(x ) 处的切线方程为
y-yo=f'(x )(x-x )
探究2:你能求出曲线y=f(x) 在点M (xo,f(xo)) 处的切线方
程是什么吗
典例精析
例1 如图1.1-3,它表
示跳水运动中高度随
时间变化的函数h(t)
=-4.9t +6.5t+10 的
图象.根据图象,请描
述、比较曲线h(t) 在t 。, 图1.1-3
t ,t 附 近 的 变 化 情 况
利用曲线在动点的切线,刻画曲线在动点附近
的变化情况.
解 我 们 用 曲 线h(x)在to,t ,t 处的切线,刻画曲
线h(t)在上述三个时刻附近的变化情况
VV
l
(1当t=to 时,曲线h(t)在
to处的切线l,平行于x轴 .
所以,在t=to 附近曲线比
较平坦,几乎没有升降
(2)当t=t 时,曲线h(t) 在 t 图1.1-3 l
处的切线l,的斜率h(t )<0. 所以,在t=t 附近曲线下 降,即函数h(t)在t=t 附近单调递减
3 当t=t 时,曲线ht) 在t 处的切线l 的斜率ht )<0.
所以,在t=t 附近曲线下降即函数h(t)在t=t, 附 近 也
单调递减
从图1.1-3可见,直线l 的倾斜程度小于直线2的倾斜
程度,这说明曲线h(t)在t附 近 比 在t 附近下降得缓慢
A
例3:曲线y=f(x)=x -1 在x=x, 处的切线与曲线
y=g(x)=1-x 在x=x,处的切线互相平行.
(1)求x 的值;(2)求曲线y=f(x) 在x=x 处的切线方程
由题意得2x =-3x , 解得x =0 或
解析:(1)
例3:曲线y=f(x)=x -1 在x=x, 处的切线与曲线
y=g(x)=1-x 在x=x, 处的切线互相平行.
(1)求x,的值;(2)求曲线y=f(x) 在x=x, 处的切线方程.
解析:(2)当x =0 时,f'(xo)=0, 又f(0)=-1,
故所求切线方程为y=-1;
A
当 时 ,
故所求切线方程
1 . 如图,直线l是曲线y=f(x) 在x=4 处的切线,则f( 4)=( )
A
1
解:根据导数的几何意义知f(4)是曲线y=f(x)在x=4 处
的切线的斜率k, 注 意 到k= , 所 以
B.3 C.4 D.5
巩固练习
2
A △
2.函数f(x)的图象如图所示,下列数值排序正确的是( A ).
(A)f'(1)>f'(2)>f'(3)>0
(B)f'(1)
A △
3.如图,函数y=f(x) 的图象在点P处的切线方程是y=-x+8 ,
则f(5)十f'(5)= 2 _
A
解析:点P横坐标为5,
故由在点P处切线为y=-x+8,
得f'(5)=-1,f(5)=-5+8=3.
∴f(5)+f'(5)=2.
y=-x+8
P
0 5 x
个y
4、已知函数f(x)的图象如图所示,则下列不等关系中正确的是
A.0
f'(2) 为函数f(x)的图象在点B(2,f(2)) 处的切线的斜率,
f'(3) 为函数f(x)的图象在点A(3,f(3)) 处的切线的斜率,
根据图象可知0
本课小结
1.切线的定义: 设Q为曲线C上不同于点P的一点,则直线PQ称 为曲线的割线.随着点Q 沿曲线C 向点P运动,当点Q 无限逼近点 P时,直线PQ 最终成为点P处最逼近曲线的直线l, 这时直线l称 为曲线在点P处的切线.
2.导数的几何意义:
函数y=f(x)在x 处的导数f'(x ), 是曲线y=f(x)在点(x ,f(xo))
处的切线的斜率. 函数y=f(x)在x 处切线的斜率反映了导数的几
何意义.
同课章节目录
