〖数学〗正弦定理(第一课时)课件(共18张PPT)-2024-2025学年高一下学期数学人教A版(2019)必修第二册
文档属性
| 名称 | 〖数学〗正弦定理(第一课时)课件(共18张PPT)-2024-2025学年高一下学期数学人教A版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 17:37:00 | ||
图片预览






文档简介
(共18张PPT)
第 6 章
平面向量及其应用
6.4.3.2 正弦定理
高一数学必修第二册(人教A版2019)
学习目标
● 1.能借助向量的运算,探索三角形边长与角度的关系.
● 2.掌握正弦定理,用向量的方法推导正弦定理.
● 3.能利用正弦定理解三角形;
● 4.三角形解的个数的判断 .
探索新知
思考1: 在上节课中,若已知两边及一角或三边,可以利用余弦定理解三角形。
那么,若已知三角形两角及一边,是否也有相应的直接解三角形的公式呢
在初中,我们得到了三角形中等边对等角的结论,实际上,三角形中还有大
边对大角,小边对小角的边角关系。
从量化的角度看,可以将这个边、角关系转化为:在△ABC 中,设A 的对边
为a,B 的对边为b, 求A,B,a,b, 之间的定量关系.从而可以解决“在△ABC中,
已A,B,a, 求b” 的问题.
思考2:向量的数量积中出现的是角的余弦,而我们需要的是角的正弦,如何实现转化
由诱导公 知,我们可以通过构造角之间的互余关系,
把边与角的余弦关系转化为正弦关系.
猜想它们之间的联系.
根据锐角三角函数,在Rt△ABC 中,有:
, 则 :
又因为sin C=sin 90°= 1, 所以
探究:通过对直角三角形的研究,观察它的角和三边之间的关系,
如图,在锐角△ABC 中,过点A 作与AC 垂直的单位向量j,
则了与AB的夹角 ,j 与CB 的 夹角
因为AC+CB=AB, 所以了 ·(AC+CB)=j·AB.
由分配律,得:了 ·AC+j ·CB=j ·AB,
思考3:对于锐角、钝角三角形以上结论是否成立
同理,过点C作与CB 垂直的单位向量m, 可
也即asin C=csin A.所以
因此,
由分配率,得:j.AC+j.CB=j.AB
即 j.
也 即a s inC=cs in A,所 以
当△ABC 是钝角三角形时,不妨设A 为钝角(如图).
过点A作与AC垂直的单位向量j,
则j 与AB 的夹角为 ,j 与CB 的夹角 ●
因为AC+CB=AB, 所以j.(AC+CB)=j·AB,
业
asinB=bsinA
即:
同 理 , 即:
asinB=bsinA
即:
业
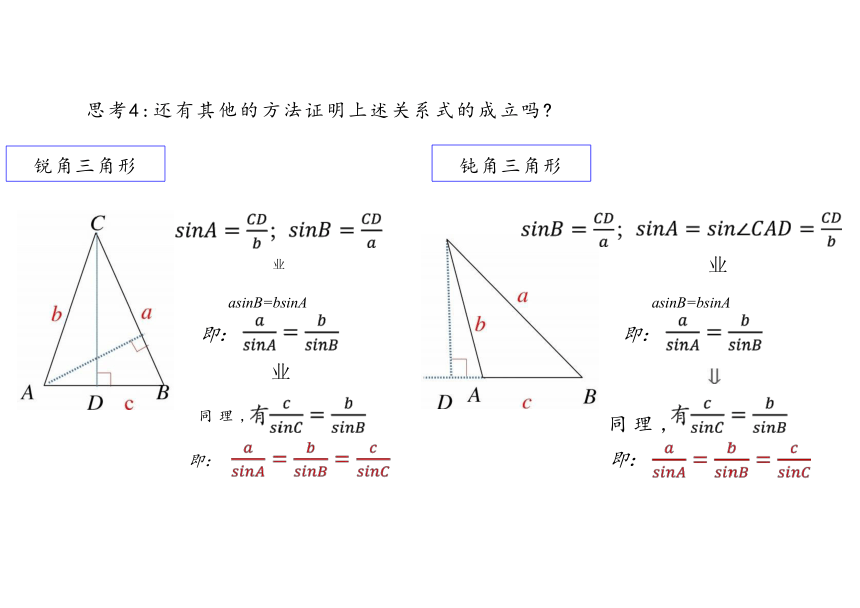
思考4:还有其他的方法证明上述关系式的成立吗
钝角三角形
锐角三角形
同 理 ,
即:
业
【问题】利用正弦定理可以解决三角形的哪类问题
【问题】正弦定理有几个等式,每个等式中有几个元素
利用正弦定理,我们可以解已知“两角和一边”和 “两边和其中一边的对角”的三角形.
学习新知
正弦定理
正弦定理中有三个等式,每个等式中有四个元素(两角及其对边) .
在一个三角形中,各边和它所对角的正弦的比相等,即:
边角互相转化
应 用 新 知
例7.在△ABC中,已知B=30°,A=15°,c=3+√3, 解这个三角形.
解:由三角形内角和定理,得:
C=180°-(A+B)=180°-(15°+30°)=120° .
由正弦定理,得:
例8.在△ABC中,已知B=30°,b=√2,c=2, 解这个三角形.
解:由正弦定理,得:
因 为c>b,B=30°, 所以30 °于是C=45°, 或C=135° . A
为什么角C有两个值
b=√2
C
c=2
30°
C
b=√2
B
① 当C=45° 时 ,A=105° .
② 当C=135° 时 ,A=15°
此时,
此时,
思考4: 在前面的例题中我们可以发现,有一些三角形有两个解,有一些有两
个解,为什么会出现这一情况
由三角函数的性质可知,
在区间(0,π)内,余弦函数单调递减,所以利用余弦定理求角,只有一解;
正弦函数在区间 内单调递增,在区间 内单调递减,所以利用正弦定
理求角,可能有两解。
【分析】由 ,可求出角B,则C=180°-(A+B), 从
【探究】在△ABC 中,已知a,b,A, 讨论三角形解的情况.
如果a≥b, 那么只有一解. A
如果a(1)若a>bsin A,则有两解.
(2)若a=bsinA, 则只有一解.
C
b a=bsinA
A B
(3)若aC
aB
a
A
B
B
2.当 A为锐角时,
b
A<
a
B
C
b
C
a
b
A为锐角 A为钝角 或直角 图形 C b a A B b A C a B C b a A B C b A
a
关系式 ab a≤b 解的个数 无解 一解 两解 一解 一解 无解
结 论 :
已知两边及其中一边的对角,用正弦定理解三角形,可能有两解、 一解或无解.在△ABC
中,已知a,b 和 A 时,解的情况如下:
全品P229
变式 (1) [2024 ·浙江四校高一月考]在△ ABC 中,内角A,B,C 的对边
分别为a,b,c, 分别根据下列条件解三角形,其中有两解的是( )
A.a =4,b=5,c=6 Ba =√3,b=2,A=45°
C.a =10,A=45°,B=70° D.a=3,b=2,A=60°
(2)在△ ABC中,内角A,B,C 所对的边分别为a,b,c, 若
b=2,A=30°, 且该三角形有唯一解,则a的取值范围为{1}U [2,+0].
(1)由正弦定理,得
因 为c( 2 ) 在 △ABC 中,已知b=2,A=45°,C=75°, 求 c.
练习(第48页)
2 . (1)在△ABC 中,已知a=2,
(2)B=180°-A-C=60° .
,A=120°, 求 b 和 C;
由正弦定理,
3.在△ABC中,已知 ,b= √3, 求a,c
因为 ,所以 于
2
第 6 章
平面向量及其应用
6.4.3.2 正弦定理
高一数学必修第二册(人教A版2019)
学习目标
● 1.能借助向量的运算,探索三角形边长与角度的关系.
● 2.掌握正弦定理,用向量的方法推导正弦定理.
● 3.能利用正弦定理解三角形;
● 4.三角形解的个数的判断 .
探索新知
思考1: 在上节课中,若已知两边及一角或三边,可以利用余弦定理解三角形。
那么,若已知三角形两角及一边,是否也有相应的直接解三角形的公式呢
在初中,我们得到了三角形中等边对等角的结论,实际上,三角形中还有大
边对大角,小边对小角的边角关系。
从量化的角度看,可以将这个边、角关系转化为:在△ABC 中,设A 的对边
为a,B 的对边为b, 求A,B,a,b, 之间的定量关系.从而可以解决“在△ABC中,
已A,B,a, 求b” 的问题.
思考2:向量的数量积中出现的是角的余弦,而我们需要的是角的正弦,如何实现转化
由诱导公 知,我们可以通过构造角之间的互余关系,
把边与角的余弦关系转化为正弦关系.
猜想它们之间的联系.
根据锐角三角函数,在Rt△ABC 中,有:
, 则 :
又因为sin C=sin 90°= 1, 所以
探究:通过对直角三角形的研究,观察它的角和三边之间的关系,
如图,在锐角△ABC 中,过点A 作与AC 垂直的单位向量j,
则了与AB的夹角 ,j 与CB 的 夹角
因为AC+CB=AB, 所以了 ·(AC+CB)=j·AB.
由分配律,得:了 ·AC+j ·CB=j ·AB,
思考3:对于锐角、钝角三角形以上结论是否成立
同理,过点C作与CB 垂直的单位向量m, 可
也即asin C=csin A.所以
因此,
由分配率,得:j.AC+j.CB=j.AB
即 j.
也 即a s inC=cs in A,所 以
当△ABC 是钝角三角形时,不妨设A 为钝角(如图).
过点A作与AC垂直的单位向量j,
则j 与AB 的夹角为 ,j 与CB 的夹角 ●
因为AC+CB=AB, 所以j.(AC+CB)=j·AB,
业
asinB=bsinA
即:
同 理 , 即:
asinB=bsinA
即:
业
思考4:还有其他的方法证明上述关系式的成立吗
钝角三角形
锐角三角形
同 理 ,
即:
业
【问题】利用正弦定理可以解决三角形的哪类问题
【问题】正弦定理有几个等式,每个等式中有几个元素
利用正弦定理,我们可以解已知“两角和一边”和 “两边和其中一边的对角”的三角形.
学习新知
正弦定理
正弦定理中有三个等式,每个等式中有四个元素(两角及其对边) .
在一个三角形中,各边和它所对角的正弦的比相等,即:
边角互相转化
应 用 新 知
例7.在△ABC中,已知B=30°,A=15°,c=3+√3, 解这个三角形.
解:由三角形内角和定理,得:
C=180°-(A+B)=180°-(15°+30°)=120° .
由正弦定理,得:
例8.在△ABC中,已知B=30°,b=√2,c=2, 解这个三角形.
解:由正弦定理,得:
因 为c>b,B=30°, 所以30 °
为什么角C有两个值
b=√2
C
c=2
30°
C
b=√2
B
① 当C=45° 时 ,A=105° .
② 当C=135° 时 ,A=15°
此时,
此时,
思考4: 在前面的例题中我们可以发现,有一些三角形有两个解,有一些有两
个解,为什么会出现这一情况
由三角函数的性质可知,
在区间(0,π)内,余弦函数单调递减,所以利用余弦定理求角,只有一解;
正弦函数在区间 内单调递增,在区间 内单调递减,所以利用正弦定
理求角,可能有两解。
【分析】由 ,可求出角B,则C=180°-(A+B), 从
【探究】在△ABC 中,已知a,b,A, 讨论三角形解的情况.
如果a≥b, 那么只有一解. A
如果a
(2)若a=bsinA, 则只有一解.
C
b a=bsinA
A B
(3)若a
a
a
A
B
B
2.当 A为锐角时,
b
A<
a
B
C
b
C
a
b
A为锐角 A为钝角 或直角 图形 C b a A B b A C a B C b a A B C b A
a
关系式 a
结 论 :
已知两边及其中一边的对角,用正弦定理解三角形,可能有两解、 一解或无解.在△ABC
中,已知a,b 和 A 时,解的情况如下:
全品P229
变式 (1) [2024 ·浙江四校高一月考]在△ ABC 中,内角A,B,C 的对边
分别为a,b,c, 分别根据下列条件解三角形,其中有两解的是( )
A.a =4,b=5,c=6 Ba =√3,b=2,A=45°
C.a =10,A=45°,B=70° D.a=3,b=2,A=60°
(2)在△ ABC中,内角A,B,C 所对的边分别为a,b,c, 若
b=2,A=30°, 且该三角形有唯一解,则a的取值范围为{1}U [2,+0].
(1)由正弦定理,得
因 为c
练习(第48页)
2 . (1)在△ABC 中,已知a=2,
(2)B=180°-A-C=60° .
,A=120°, 求 b 和 C;
由正弦定理,
3.在△ABC中,已知 ,b= √3, 求a,c
因为 ,所以 于
2
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
