〖数学〗余弦定理课件(共19张PPT)-2024-2025学年高一下学期数学人教A版(2019)必修第二册
文档属性
| 名称 | 〖数学〗余弦定理课件(共19张PPT)-2024-2025学年高一下学期数学人教A版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 792.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 17:38:07 | ||
图片预览





文档简介
(共19张PPT)
第 6 章
平面向量及其应用
6.4.3.1 余弦定理
高一数学必修第二册(人教A 版2019)
引入新知
一个三角形含有各种各样的几何量,例如三边边长、三个内角的度数、面积
等,它们之间存在着确定的关系。
例如,在初中,我们得到过勾股定理、锐角三角函数,这是直角三角形中的边、角定量关系.
对于一般三角形,我们已经定性地研究过三角形的边、角关系,得到了SSS,SAS,ASA , AAS等判定三角形全等的方法.这些判定方法表明,给定三角形的三个角、三条边这六个元 素中的某些元素,这个三角形就是唯一确定的。
那么三角形的其他元素与给定的某些元素有怎样的数量关系
下面我们利用向量方法来研究这个问题.
探究新知
我们知道,两边和它们的夹角分别相等的两个三角形全等 (SAS).
这说明,给定两边及其夹角的三角形是唯一确定的.
也就是说,三角形的其他边、角都可以用这两边及其夹角来表示.
那么,表示的公式是什么呢
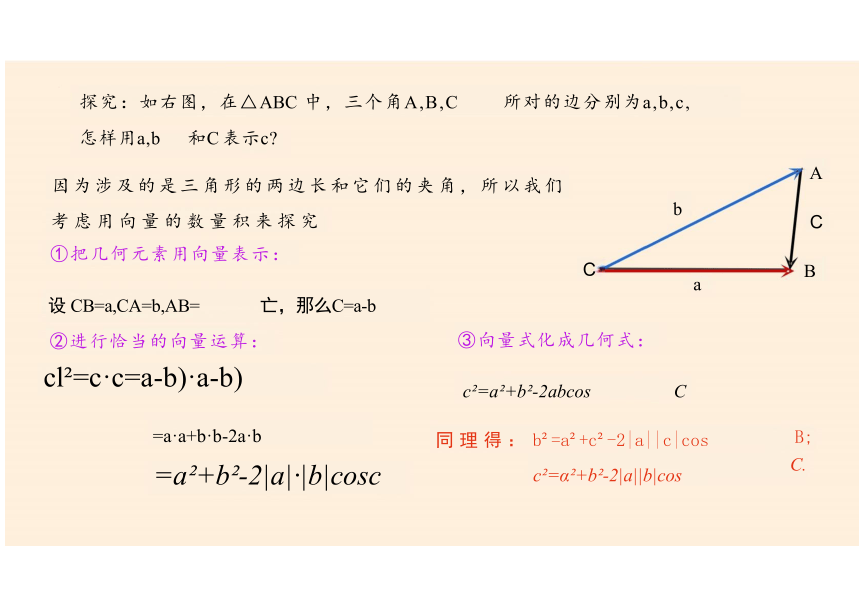
探究:如右图,在△ABC 中,三个角A,B,C 所对的边分别为a,b,c,
怎样用a,b 和C 表示c
因为涉及的是三角形的两边长和它们的夹角,所以我们
考虑用向量的数量积来探究
①把几何元素用向量表示:
设 CB=a,CA=b,AB= 亡,那么C=a-b
②进行恰当的向量运算:
cl =c·c=a-b)·a-b)
=a·a+b·b-2a·b 同 理 得 : b =a +c -2|a||c|cos =a +b -2|a|·|b|cosc c =α +b -2|a||b|cos
C
③向量式化成几何式:
c =a +b -2abcos
A
C
B
B;
C.
b
a
C
学习新知
余弦定理
三角形中任何一边的平方,等于其他两边平方的和减去
这两边与他们夹角的余弦的积的两倍.即
【问题】利用余弦定理可以解决三角形的哪类问题
利用余弦定理,我们可以从三角形已知的两边及其夹角直接求出第三边.
a =b +c -2
b =a +c -2
c =a +b -2
cos
cos
cos
A;
B; C.
b
a
a
|| ||
||
c
c b
思考1:你能用其它方法证明余弦定理吗 坐标法
在AABC 中,内角A,B,C 所对的边分别为a,b,c, 如图以点A为坐标原点,边AB 所
在直线为x轴,建立平面直角坐标系,则A(0,0),B(c,0),C(b cosA,b sinA)
由两点间距离公式得:
BC =(bcos A-c) +(bsin
=b cos2A-2bc
=b +c2-2bc cosA
即 a =b+c -2bccos A
同理可证 b =a +c -2accos
A-0)
cosA+c +b sin A
B,c =a +b -2abcos
C(b cosA,b sinA)
b 儿
C B (c,0)
X
yA
0(A)
C
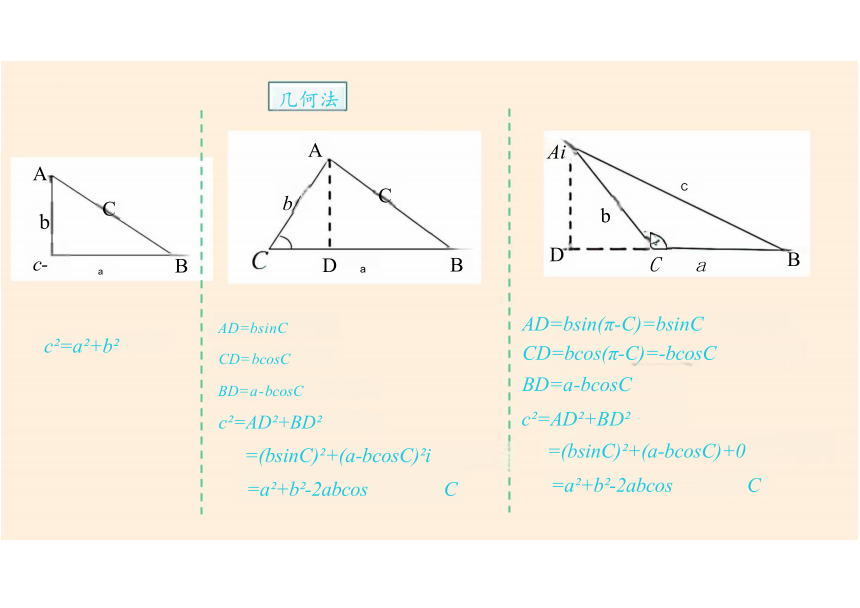
AD=bsin(π-C)=bsinC
CD=bcos(π-C)=-bcosC BD=a-bcosC
c =AD +BD
=(bsinC) +(a-bcosC)+0
=a +b -2abcos C
AD=bsinC
CD=bcosC
BD=a-bcosC
c =AD +BD
=(bsinC) +(a-bcosC) i
=a +b -2abcos C
C
b
C a
C
a B
A
b/
D
Ai
D
A
b
c-
几何法
C
a
c =a +b
B
B
怎样确定呢
a =b +c -2bccos A >
b =a +c -2accos B
c =a +b -2abcos C
余弦定理及其推论把用"SAS" 和 “SSS”判定三角形全等的方 法从数量化的角度进行了刻画.
思考2:余弦定理指出了三角形的三条边与其中的一个角之间的关系.应
用余弦定理,我们可以解决已知三角形的三边确定三角形的角的问题,
从余弦定理及其推论可以看出,
三角函数把几何中关于三角形的定 性结论变成了可定量计算的公式!
形的三边与其中的一个角之间的关系.你能说说这两个定理之间的关系吗
当C=90° 时 ,cosC=0, 则
勾股定理
由此可见,余弦定理是勾股定理的推广,而勾股定理是余弦定理的特例.
一般地,三角形的三个角A,B,C 和它们的对边a,b,c 叫做三角形的元素.
已知三角形中的几个元素求其他元素的过程叫做解三角形.
思考3:勾股定理指出了直角三角形中三边之间的关系,余弦定理指出了三角
思考4: 当角C为直角时,有c =a +b , 当角C为锐角时,这三者的关
系是什么 钝角呢
2+
g(x)=cos(x)
c 为钝角 一
C 为直角
作 2
2n
π
应用新知
例5.在△ABC 中,已知b=60 cm,c=34 cm,A=41°,解这个三角形
(角度精确到1°,边长精确到1 cm).
解:由余弦定理,得:
a =b +c -2|b||c|cos A=60 +34 -2×60×34×cos 41°≈1676.78,
利用计算器,可得B≈106°.
所以C=180°-(A+B)≈180°-(41°+106°)=33° .
所以a≈41(cm).
由余弦定理的推论,得:
例6.在△ABC 中 ,a=7,b=8, 锐角C满, 求B(精确到1°).
解:因为 , 且C为锐角,
由余弦定理,得:
所以C=3.
利用计算器,可得B≈98° .
典例分析
探究点一已知两边和一个角解三角形
例 1 (1) 在△ ABC中,内角A,B,C 的对边分别为a,b,c. 若
C=3A+3B,b=2,a=√2, 则c=( )
A.√2 C.√7 D.√2+1
变式(1) △ ABC 的内角A,B,C 所对的边分别为a,b,c,已知
C=120°,a,b 是方程x -3x+2=0 的两个根,则c的值为( )
A.√3 B.7 C.3
(2) (多选题)已知△ ABC 的内角A,B,C 所对的边分别为a,b,
C, ,a=m,b=4, 若满足条件的△ ABC 有两个,则m 的值
可以是( )
A.2√2 v2 √3 D.4
探究点二已知三边解三角形
例2(1) 在△ ABC中,内角A,B,C 的对边分别为a,b,c, 若
, 求cos B.
解:因为 , 所 以 , 所 以
则由余弦定理得
变式(1) 已知锐角三角形的三边长为2,3,x, 则x的取值范围是( )
A.(1,5) B.(1,√5) √5, √ 13) D.(√ 13,5)
[素养小结]
(1)已知三边求角的基本思路是:利用余弦定理的推论求出相应角 的余弦值,值为正,角为锐角,值为负,角为钝角,其思路清晰,
结果唯一.
(2)若已知三角形的三边的关系或比例关系,常根据边的关系直接 代入化简或利用比例性质,转化为已知三边求解.
探究点三利用余弦定理判断三角形的形状
变式(1)在△ABC中,若AB·BC+AB =0, 则△ ABC一定是( )
A.等边三角形 B. 直角三角形
C.等腰三角形 D.等腰直角三角形
(2)在△ABC中 ,(a+b+c)(a+b-c)=3ab 且2cos Asin B=sin C,
则△ ABC 是 等边三角形
[素养小结]
利用余弦定理判断三角形形状的两种途径
(1) 化边的关系:将条件中的角的关系,利用余弦定理化为边的关 系,再进行判断.
(2) 化角的关系:将条件中边的关系,通过余弦定理或三角恒等变 换变形,得到角与角之间的关系,再进行判断.
学习目标
1.了解向量法证明余弦定理的推导过程.
2.掌握余弦定理及其推论,并能用其解决一些简单的三角形度量问题 .
3.能应用余弦定理判断三角形的形状.
第 6 章
平面向量及其应用
6.4.3.1 余弦定理
高一数学必修第二册(人教A 版2019)
引入新知
一个三角形含有各种各样的几何量,例如三边边长、三个内角的度数、面积
等,它们之间存在着确定的关系。
例如,在初中,我们得到过勾股定理、锐角三角函数,这是直角三角形中的边、角定量关系.
对于一般三角形,我们已经定性地研究过三角形的边、角关系,得到了SSS,SAS,ASA , AAS等判定三角形全等的方法.这些判定方法表明,给定三角形的三个角、三条边这六个元 素中的某些元素,这个三角形就是唯一确定的。
那么三角形的其他元素与给定的某些元素有怎样的数量关系
下面我们利用向量方法来研究这个问题.
探究新知
我们知道,两边和它们的夹角分别相等的两个三角形全等 (SAS).
这说明,给定两边及其夹角的三角形是唯一确定的.
也就是说,三角形的其他边、角都可以用这两边及其夹角来表示.
那么,表示的公式是什么呢
探究:如右图,在△ABC 中,三个角A,B,C 所对的边分别为a,b,c,
怎样用a,b 和C 表示c
因为涉及的是三角形的两边长和它们的夹角,所以我们
考虑用向量的数量积来探究
①把几何元素用向量表示:
设 CB=a,CA=b,AB= 亡,那么C=a-b
②进行恰当的向量运算:
cl =c·c=a-b)·a-b)
=a·a+b·b-2a·b 同 理 得 : b =a +c -2|a||c|cos =a +b -2|a|·|b|cosc c =α +b -2|a||b|cos
C
③向量式化成几何式:
c =a +b -2abcos
A
C
B
B;
C.
b
a
C
学习新知
余弦定理
三角形中任何一边的平方,等于其他两边平方的和减去
这两边与他们夹角的余弦的积的两倍.即
【问题】利用余弦定理可以解决三角形的哪类问题
利用余弦定理,我们可以从三角形已知的两边及其夹角直接求出第三边.
a =b +c -2
b =a +c -2
c =a +b -2
cos
cos
cos
A;
B; C.
b
a
a
|| ||
||
c
c b
思考1:你能用其它方法证明余弦定理吗 坐标法
在AABC 中,内角A,B,C 所对的边分别为a,b,c, 如图以点A为坐标原点,边AB 所
在直线为x轴,建立平面直角坐标系,则A(0,0),B(c,0),C(b cosA,b sinA)
由两点间距离公式得:
BC =(bcos A-c) +(bsin
=b cos2A-2bc
=b +c2-2bc cosA
即 a =b+c -2bccos A
同理可证 b =a +c -2accos
A-0)
cosA+c +b sin A
B,c =a +b -2abcos
C(b cosA,b sinA)
b 儿
C B (c,0)
X
yA
0(A)
C
AD=bsin(π-C)=bsinC
CD=bcos(π-C)=-bcosC BD=a-bcosC
c =AD +BD
=(bsinC) +(a-bcosC)+0
=a +b -2abcos C
AD=bsinC
CD=bcosC
BD=a-bcosC
c =AD +BD
=(bsinC) +(a-bcosC) i
=a +b -2abcos C
C
b
C a
C
a B
A
b/
D
Ai
D
A
b
c-
几何法
C
a
c =a +b
B
B
怎样确定呢
a =b +c -2bccos A >
b =a +c -2accos B
c =a +b -2abcos C
余弦定理及其推论把用"SAS" 和 “SSS”判定三角形全等的方 法从数量化的角度进行了刻画.
思考2:余弦定理指出了三角形的三条边与其中的一个角之间的关系.应
用余弦定理,我们可以解决已知三角形的三边确定三角形的角的问题,
从余弦定理及其推论可以看出,
三角函数把几何中关于三角形的定 性结论变成了可定量计算的公式!
形的三边与其中的一个角之间的关系.你能说说这两个定理之间的关系吗
当C=90° 时 ,cosC=0, 则
勾股定理
由此可见,余弦定理是勾股定理的推广,而勾股定理是余弦定理的特例.
一般地,三角形的三个角A,B,C 和它们的对边a,b,c 叫做三角形的元素.
已知三角形中的几个元素求其他元素的过程叫做解三角形.
思考3:勾股定理指出了直角三角形中三边之间的关系,余弦定理指出了三角
思考4: 当角C为直角时,有c =a +b , 当角C为锐角时,这三者的关
系是什么 钝角呢
2+
g(x)=cos(x)
c 为钝角 一
C 为直角
作 2
2n
π
应用新知
例5.在△ABC 中,已知b=60 cm,c=34 cm,A=41°,解这个三角形
(角度精确到1°,边长精确到1 cm).
解:由余弦定理,得:
a =b +c -2|b||c|cos A=60 +34 -2×60×34×cos 41°≈1676.78,
利用计算器,可得B≈106°.
所以C=180°-(A+B)≈180°-(41°+106°)=33° .
所以a≈41(cm).
由余弦定理的推论,得:
例6.在△ABC 中 ,a=7,b=8, 锐角C满, 求B(精确到1°).
解:因为 , 且C为锐角,
由余弦定理,得:
所以C=3.
利用计算器,可得B≈98° .
典例分析
探究点一已知两边和一个角解三角形
例 1 (1) 在△ ABC中,内角A,B,C 的对边分别为a,b,c. 若
C=3A+3B,b=2,a=√2, 则c=( )
A.√2 C.√7 D.√2+1
变式(1) △ ABC 的内角A,B,C 所对的边分别为a,b,c,已知
C=120°,a,b 是方程x -3x+2=0 的两个根,则c的值为( )
A.√3 B.7 C.3
(2) (多选题)已知△ ABC 的内角A,B,C 所对的边分别为a,b,
C, ,a=m,b=4, 若满足条件的△ ABC 有两个,则m 的值
可以是( )
A.2√2 v2 √3 D.4
探究点二已知三边解三角形
例2(1) 在△ ABC中,内角A,B,C 的对边分别为a,b,c, 若
, 求cos B.
解:因为 , 所 以 , 所 以
则由余弦定理得
变式(1) 已知锐角三角形的三边长为2,3,x, 则x的取值范围是( )
A.(1,5) B.(1,√5) √5, √ 13) D.(√ 13,5)
[素养小结]
(1)已知三边求角的基本思路是:利用余弦定理的推论求出相应角 的余弦值,值为正,角为锐角,值为负,角为钝角,其思路清晰,
结果唯一.
(2)若已知三角形的三边的关系或比例关系,常根据边的关系直接 代入化简或利用比例性质,转化为已知三边求解.
探究点三利用余弦定理判断三角形的形状
变式(1)在△ABC中,若AB·BC+AB =0, 则△ ABC一定是( )
A.等边三角形 B. 直角三角形
C.等腰三角形 D.等腰直角三角形
(2)在△ABC中 ,(a+b+c)(a+b-c)=3ab 且2cos Asin B=sin C,
则△ ABC 是 等边三角形
[素养小结]
利用余弦定理判断三角形形状的两种途径
(1) 化边的关系:将条件中的角的关系,利用余弦定理化为边的关 系,再进行判断.
(2) 化角的关系:将条件中边的关系,通过余弦定理或三角恒等变 换变形,得到角与角之间的关系,再进行判断.
学习目标
1.了解向量法证明余弦定理的推导过程.
2.掌握余弦定理及其推论,并能用其解决一些简单的三角形度量问题 .
3.能应用余弦定理判断三角形的形状.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
