〖数学〗导数的几何意义课件(共20张PPT)-2024-2025学年高二下学期数学北师大版(2019)选择性必修第二册
文档属性
| 名称 | 〖数学〗导数的几何意义课件(共20张PPT)-2024-2025学年高二下学期数学北师大版(2019)选择性必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 17:39:14 | ||
图片预览




文档简介
(共20张PPT)
导数的几何意义
复习引入
1.函数y=f(x)在x=x, 处的导数
设函数y=f(x), 当自变量x从x 变到x 时,函数值y从f(xo)变到f(x ),
< 平均变化率趋于一个固定的值,我们称这个值为平均变化率的极限,记作
口 那么这个值就是函数y=f(x) 在点x 的瞬时变化率
, 也叫y=f(x) 在点x 的导数。
2.求函数y=f(x)在x=x, 处导数的步骤
(1)求函数的增量△y=f(x +△x)-f(x );
(2)求平均变化率
(3)取极限,得导
新课探究
探究1: 我们知道,导数f(xo)表示函数y=f(x) 在x=x 处
的瞬时变化率,反映了函数y=f(x) 在x=x 附近的变化情况.
平均变化率 瞬时变化率 .导数
平均变化率的几何意义 导数f( xo)的几何意义
那么导数f(x ) 的几何意义是什么
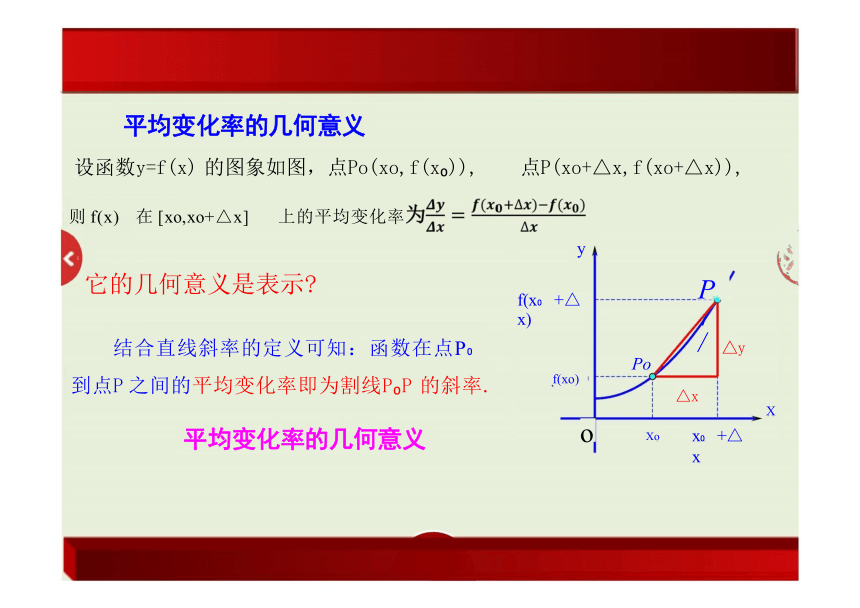
结合直线斜率的定义可知:函数在点P
到点P 之间的平均变化率即为割线P P 的斜率.
平均变化率的几何意义
平均变化率的几何意义
设函数y=f(x) 的图象如图,点Po(xo,f(x )), 点P(xo+△x,f(xo+△x)),
则 f(x) 在 [xo,xo+△x] 上的平均变化率
它的几何意义是表示
△y
△x
x +△x
y
f(x +△x)
f(xo)
o
Po
Xo
P /
X
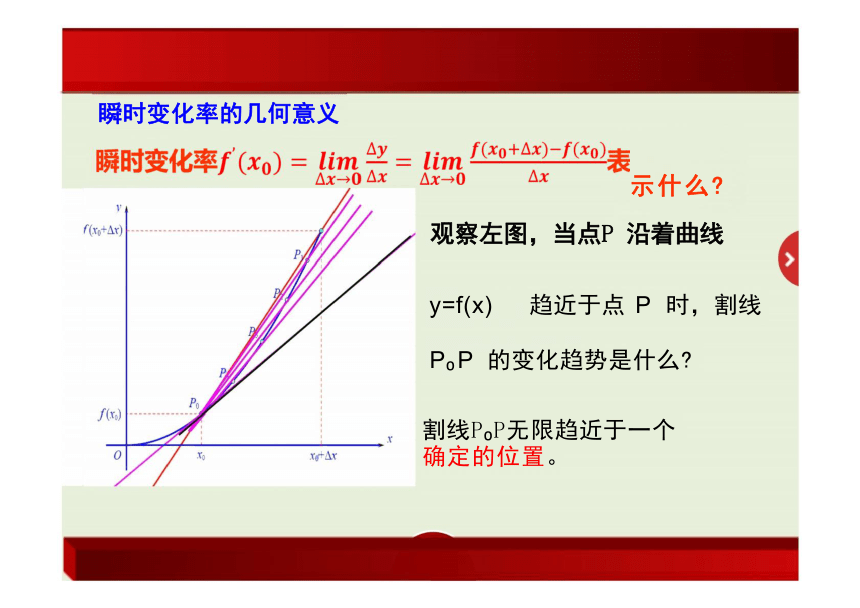
瞬时变化率的几何意义
示什么
观察左图,当点P 沿着曲线
y=f(x) 趋近于点 P 时,割线
P P 的变化趋势是什么
割线P P无限趋近于一个 确定的位置。
新课讲授
1.切线的定义
在曲线y=f(x) 上任取一点P(x,f(x))
当点P(x,f(x))沿着曲线y=f(x) 无限趋近于点P。(xo,f(xo) )时,割线P P无限趋近于一个确定的位置,这个确定的位置 的直线P T 称为曲线y=f(x) 在点P,处的切线.
思考1: 此处的切线定义与初中学过的圆的切线定义有什么
不同
此处的切线定义是以逼近的方式对切线作出的定义;
初中学过的圆的切线是从直线和圆的公共点个数的角度定义的.
思考2: 通过逼近方式对切线作出的定义,是否适用于圆
的切线呢
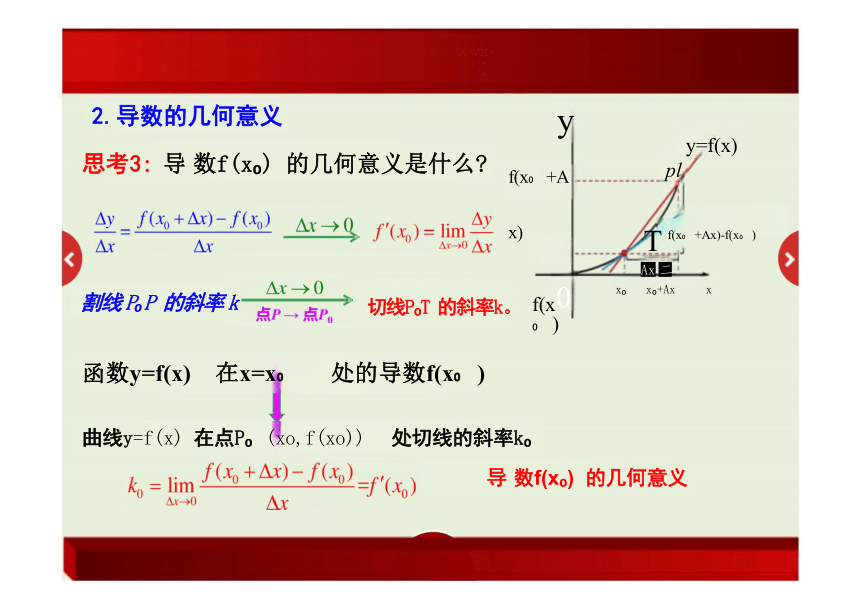
割线 P P 的斜率 k 切线P T 的斜率k。 0
函数y=f(x) 在x=x 处的导数f(x )
曲线y=f(x) 在点P (xo,f(xo)) 处切线的斜率k
2.导数的几何意义
思考3: 导 数f(x ) 的几何意义是什么
y=f(x) pl
T f(x +Ax)-f(x )
Ax 二
x x +Ax x
y
f(x +Ax)
f(x )
导 数f(x ) 的几何意义
可 合
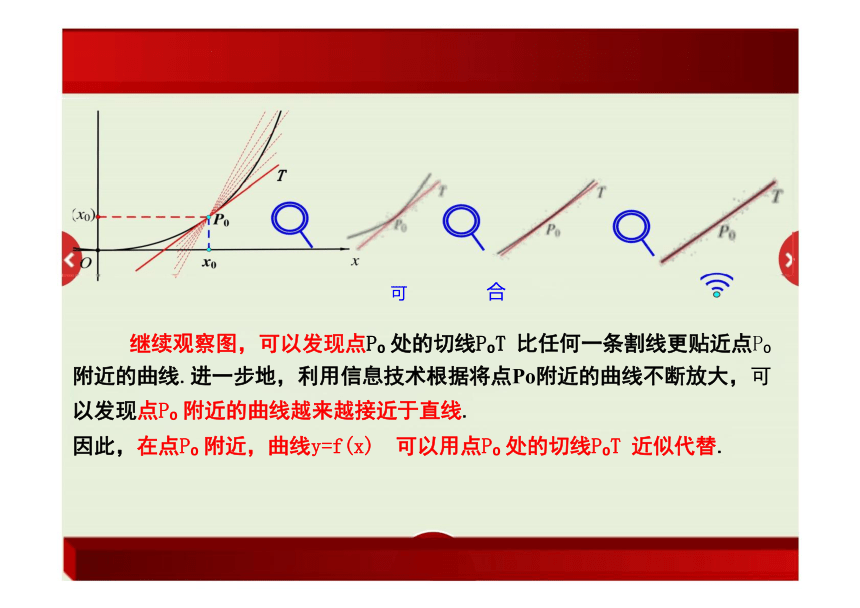
继续观察图,可以发现点P 处的切线P T 比任何一条割线更贴近点P
附近的曲线.进一步地,利用信息技术根据将点Po附近的曲线不断放大,可 以发现点P 附近的曲线越来越接近于直线.
因此,在点P 附近,曲线y=f(x) 可以用点P 处的切线P T 近似代替.
=f'(x )
即 kpr=tan α=f'(x )
曲线y=f(x) 在点M(x ,f(x ) 处的切线方程为
y-yo=f'(x )(x-xo)
探究2: 你能求出曲线y=f(x) 在点M (xo,f(xo)) 处的切线方
程是什么吗
品 y2●2(xO1J2xoyO0.
解决切线问题的关键:利用导数的几何意义求出切线的斜率 k =f'(x ).
典例精析
例 1 : 求曲线f(x)=x +1
(x)■x
在点P(1,2) 处的切线方程.
P(1,2)
求曲线在某点处的切线方程的步骤
求斜率 求 出 曲 线 在 点(x ,f(x ))处切线的斜率f'(xo)
写方程 用 点 斜 式y-f(x )=f'(xo)(x-x )写 出 切 线 方 程
变 形 将点斜式变为一般式
令△x趋于0,可知y=2x 在x=1 处的导数为f'(1)=6.
于是,函数y =2x 在点(1, f(1))即(1,2)处的切线斜率为6,
即该切线经过点(1,2), 且斜率为6.
因此,函数y =f(x)=2x 在x= 1处的切线方程为:
y-2=6(x-1), 即y=6x-4.
例2: 求函数y=f(x)=2x 在x=1 处的切线方程.
例3:曲线y=f(x)=x -1 在x=x, 处的切线与曲线
y=g(x)=1-x 在x=x,处的切线互相平行.
(1)求x,的值;(2)求曲线y=f(x) 在x=x,处的切线方程.
由题意得2x =-3x , 解得x =0 或
解析:(
例3: 曲线y =f(x)=x -1 在x=x, 处的切线与曲线
y=g(x)=1-x 在x=x, 处的切线互相平行.
(1)求x,的值;(2)求曲线y=f(x) 在x=x, 处的切线方程.
解析: (2)当x =0 时 ,f'(xo)=0, 又f(0)=-1, 故所求切线方程为y=-1;
故所求切线方程
当 时,
巩固练习
1. 如图,直线l是曲线y=f(x)在 x=4 处的切线,则f(4)=( )
B.3 C.4 D.5
解:根据导数的几何意义知f(4) 是曲线y=f(x) 在x=4 处
的切线的斜率k, 注 意 到 , 所 以
(A)f'(1)>f'(2)>f'(3)>0
(B)f'(1)(C)0(D)f'(1)>f'(2)>0>f'(3)
2.函数f(x)的图象如图所示,下列数值排序正确的是( A ).
3.如图,函数y=f(x) 的图象在点P 处的切线方程是y=-x+8 ,
则f(5)+f'(5)= 2 4y y=-x+8
P
A
解析:点P横坐标为5,
故由在点P处切线为y=-x+8,
得f'(5)=-1,f(5)=-5+8=3.
∴f(5)+f'(5)=2.
>
5
0
4.直 是函数 象的切线,则切点是
1或 - 1 ( - 2, - )或
斋
解得x=±2.
当x=-2 时, ,b=-1;
当x=2 时, ,b=1.
本课小结
1.切线的定义: 设Q为曲线C上不同于点P的一点,则直线PQ称 为曲线的割线.随着点Q 沿曲线C 向点P运动,当点Q 无限逼近点
P时,直线PQ 最终成为点P 处最逼近曲线的直线l, 这时直线l称 为曲线在点P处的切线.
2.导数的几何意义:
函数y=f(x) 在x 处的导数f'(x ), 是曲线y=f(x) 在点(xo,f(xo))
处的切线的斜率. 函数y=f(x)在x 处切线的斜率反映了导数的几 何意义.
导数的几何意义
复习引入
1.函数y=f(x)在x=x, 处的导数
设函数y=f(x), 当自变量x从x 变到x 时,函数值y从f(xo)变到f(x ),
< 平均变化率趋于一个固定的值,我们称这个值为平均变化率的极限,记作
口 那么这个值就是函数y=f(x) 在点x 的瞬时变化率
, 也叫y=f(x) 在点x 的导数。
2.求函数y=f(x)在x=x, 处导数的步骤
(1)求函数的增量△y=f(x +△x)-f(x );
(2)求平均变化率
(3)取极限,得导
新课探究
探究1: 我们知道,导数f(xo)表示函数y=f(x) 在x=x 处
的瞬时变化率,反映了函数y=f(x) 在x=x 附近的变化情况.
平均变化率 瞬时变化率 .导数
平均变化率的几何意义 导数f( xo)的几何意义
那么导数f(x ) 的几何意义是什么
结合直线斜率的定义可知:函数在点P
到点P 之间的平均变化率即为割线P P 的斜率.
平均变化率的几何意义
平均变化率的几何意义
设函数y=f(x) 的图象如图,点Po(xo,f(x )), 点P(xo+△x,f(xo+△x)),
则 f(x) 在 [xo,xo+△x] 上的平均变化率
它的几何意义是表示
△y
△x
x +△x
y
f(x +△x)
f(xo)
o
Po
Xo
P /
X
瞬时变化率的几何意义
示什么
观察左图,当点P 沿着曲线
y=f(x) 趋近于点 P 时,割线
P P 的变化趋势是什么
割线P P无限趋近于一个 确定的位置。
新课讲授
1.切线的定义
在曲线y=f(x) 上任取一点P(x,f(x))
当点P(x,f(x))沿着曲线y=f(x) 无限趋近于点P。(xo,f(xo) )时,割线P P无限趋近于一个确定的位置,这个确定的位置 的直线P T 称为曲线y=f(x) 在点P,处的切线.
思考1: 此处的切线定义与初中学过的圆的切线定义有什么
不同
此处的切线定义是以逼近的方式对切线作出的定义;
初中学过的圆的切线是从直线和圆的公共点个数的角度定义的.
思考2: 通过逼近方式对切线作出的定义,是否适用于圆
的切线呢
割线 P P 的斜率 k 切线P T 的斜率k。 0
函数y=f(x) 在x=x 处的导数f(x )
曲线y=f(x) 在点P (xo,f(xo)) 处切线的斜率k
2.导数的几何意义
思考3: 导 数f(x ) 的几何意义是什么
y=f(x) pl
T f(x +Ax)-f(x )
Ax 二
x x +Ax x
y
f(x +Ax)
f(x )
导 数f(x ) 的几何意义
可 合
继续观察图,可以发现点P 处的切线P T 比任何一条割线更贴近点P
附近的曲线.进一步地,利用信息技术根据将点Po附近的曲线不断放大,可 以发现点P 附近的曲线越来越接近于直线.
因此,在点P 附近,曲线y=f(x) 可以用点P 处的切线P T 近似代替.
=f'(x )
即 kpr=tan α=f'(x )
曲线y=f(x) 在点M(x ,f(x ) 处的切线方程为
y-yo=f'(x )(x-xo)
探究2: 你能求出曲线y=f(x) 在点M (xo,f(xo)) 处的切线方
程是什么吗
品 y2●2(xO1J2xoyO0.
解决切线问题的关键:利用导数的几何意义求出切线的斜率 k =f'(x ).
典例精析
例 1 : 求曲线f(x)=x +1
(x)■x
在点P(1,2) 处的切线方程.
P(1,2)
求曲线在某点处的切线方程的步骤
求斜率 求 出 曲 线 在 点(x ,f(x ))处切线的斜率f'(xo)
写方程 用 点 斜 式y-f(x )=f'(xo)(x-x )写 出 切 线 方 程
变 形 将点斜式变为一般式
令△x趋于0,可知y=2x 在x=1 处的导数为f'(1)=6.
于是,函数y =2x 在点(1, f(1))即(1,2)处的切线斜率为6,
即该切线经过点(1,2), 且斜率为6.
因此,函数y =f(x)=2x 在x= 1处的切线方程为:
y-2=6(x-1), 即y=6x-4.
例2: 求函数y=f(x)=2x 在x=1 处的切线方程.
例3:曲线y=f(x)=x -1 在x=x, 处的切线与曲线
y=g(x)=1-x 在x=x,处的切线互相平行.
(1)求x,的值;(2)求曲线y=f(x) 在x=x,处的切线方程.
由题意得2x =-3x , 解得x =0 或
解析:(
例3: 曲线y =f(x)=x -1 在x=x, 处的切线与曲线
y=g(x)=1-x 在x=x, 处的切线互相平行.
(1)求x,的值;(2)求曲线y=f(x) 在x=x, 处的切线方程.
解析: (2)当x =0 时 ,f'(xo)=0, 又f(0)=-1, 故所求切线方程为y=-1;
故所求切线方程
当 时,
巩固练习
1. 如图,直线l是曲线y=f(x)在 x=4 处的切线,则f(4)=( )
B.3 C.4 D.5
解:根据导数的几何意义知f(4) 是曲线y=f(x) 在x=4 处
的切线的斜率k, 注 意 到 , 所 以
(A)f'(1)>f'(2)>f'(3)>0
(B)f'(1)
2.函数f(x)的图象如图所示,下列数值排序正确的是( A ).
3.如图,函数y=f(x) 的图象在点P 处的切线方程是y=-x+8 ,
则f(5)+f'(5)= 2 4y y=-x+8
P
A
解析:点P横坐标为5,
故由在点P处切线为y=-x+8,
得f'(5)=-1,f(5)=-5+8=3.
∴f(5)+f'(5)=2.
>
5
0
4.直 是函数 象的切线,则切点是
1或 - 1 ( - 2, - )或
斋
解得x=±2.
当x=-2 时, ,b=-1;
当x=2 时, ,b=1.
本课小结
1.切线的定义: 设Q为曲线C上不同于点P的一点,则直线PQ称 为曲线的割线.随着点Q 沿曲线C 向点P运动,当点Q 无限逼近点
P时,直线PQ 最终成为点P 处最逼近曲线的直线l, 这时直线l称 为曲线在点P处的切线.
2.导数的几何意义:
函数y=f(x) 在x 处的导数f'(x ), 是曲线y=f(x) 在点(xo,f(xo))
处的切线的斜率. 函数y=f(x)在x 处切线的斜率反映了导数的几 何意义.
同课章节目录
