〖数学〗函数的单调性课件(共25张PPT)-2024-2025学年高二下学期数学北师大版(2019)选择性必修第二册
文档属性
| 名称 | 〖数学〗函数的单调性课件(共25张PPT)-2024-2025学年高二下学期数学北师大版(2019)选择性必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 894.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
2.6.1函数的单调性
北师大版(2019)选择性必修第二册
第二章导数及其应用
学习目标
理解导数与函数的单调性的关系.
掌握利用导数判断函数单调性的方法.
会用导数求函数的单调区间.
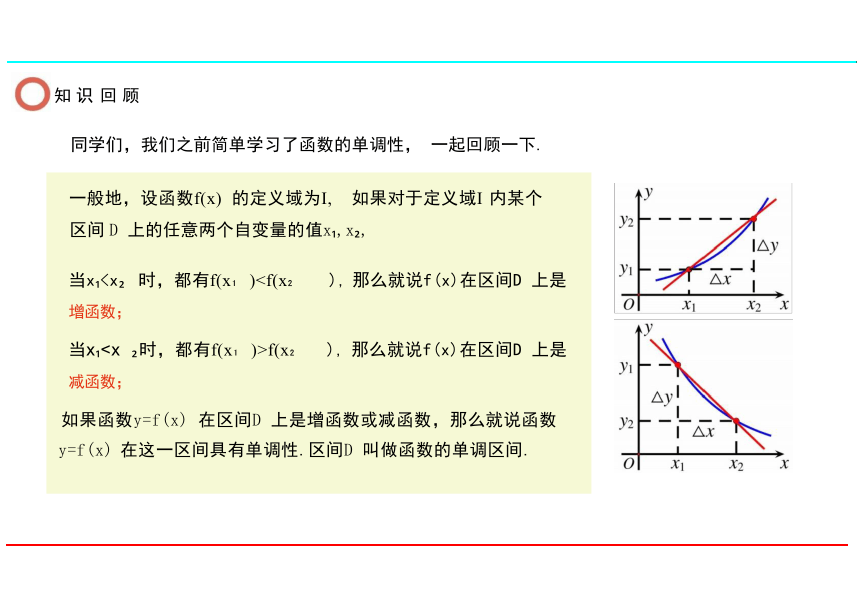
同学们,我们之前简单学习了函数的单调性, 一起回顾一下.
一般地,设函数f(x) 的定义域为I, 如果对于定义域I 内某个
区间 D 上的任意两个自变量的值x ,x ,
当x增函数;
当xf(x ), 那么就说f(x)在区间D 上是
减函数;
如果函数y=f(x) 在区间D 上是增函数或减函数,那么就说函数
y=f(x) 在这一区间具有单调性.区间D 叫做函数的单调区间.
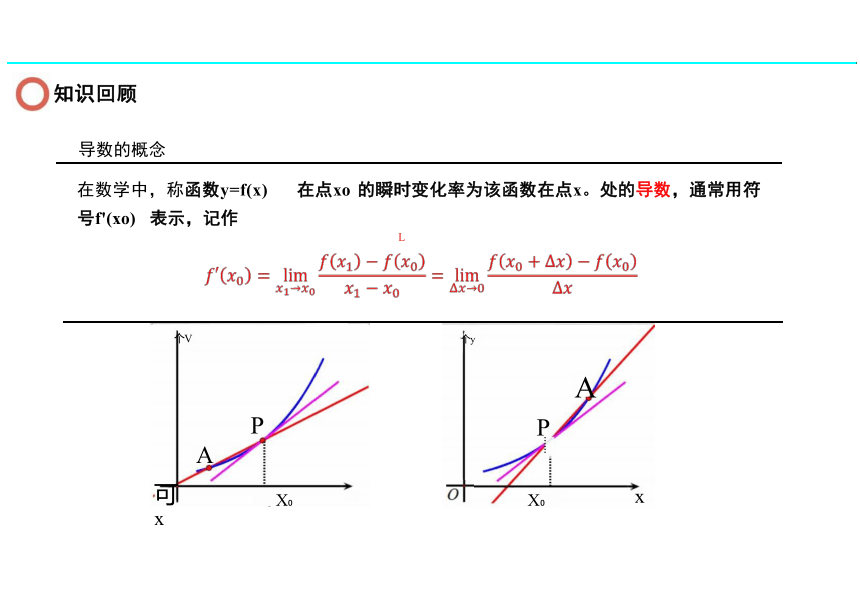
知 识 回 顾
在数学中,称函数y=f(x) 在点xo 的瞬时变化率为该函数在点x。处的导数,通常用符
号f'(xo) 表示,记作
L
个y
A
P
X x
个V
P
A
可 X x
知识回顾
导数的概念
……
问题提出
我们知道,对于函数y=f(x) 来说,导数f'(x)刻画的是函数y=f(x)
在点x 的瞬时变化率,函数的单调性描述的是函数值y 随自变量x 取值 的增加而增加,或函数值y 随自变量x 取值的增加而减少.
两者都在刻画函数的变化,那么,导数与函数的单调性之间有何关系
呢
解: (1) f'(x)=1;(2)f'(x)=2;(3)f'(x)=-3 函数(1)(2)的导数都是正的,在定义域(-0,+0)内 函数值都是随x 的增加而增加的; 函数(3)的导数是负的,在定义域(-o,+o) 内函数 值是随x 的增加而减少的. y ,y=2x+5 y=x 0 y=-3x+4
X
实例分析
1.计算下面几个一次函数的导数,并讨论它们的单调性.
(1)y=f(x)=x (2)y=f(x)=2x+5 (3)y=f(x)=-3x+4
(1) (2) (3) (4)
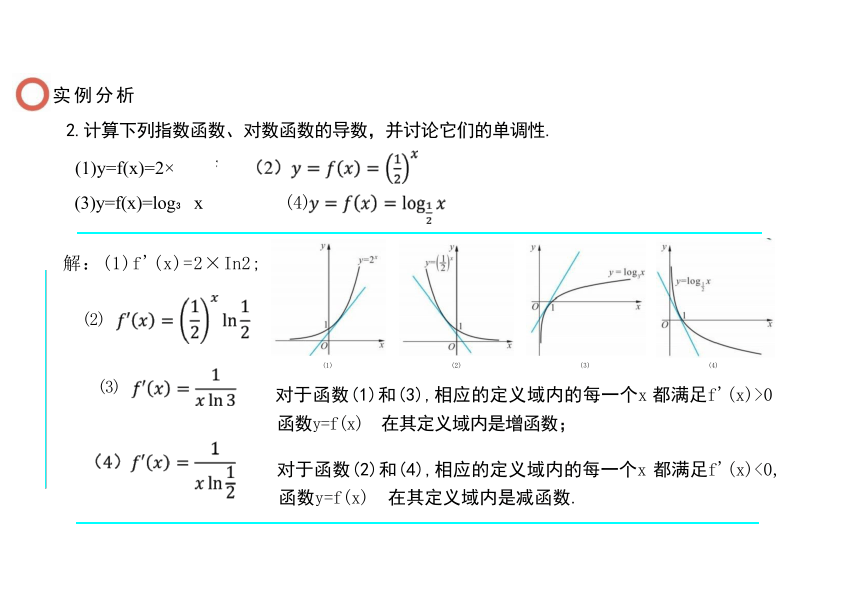
对于函数(1)和(3),相应的定义域内的每一个x 都满足f'(x)>0
函数y=f(x) 在其定义域内是增函数;
对于函数(2)和(4),相应的定义域内的每一个x 都满足f'(x)<0,
函数y=f(x) 在其定义域内是减函数.
2.计算下列指数函数、对数函数的导数,并讨论它们的单调性.
(1)y=f(x)=2×
(3)y=f(x)=log x (4)
解:(1)f'(x)=2×In2;
实例分析
(2)
(3)
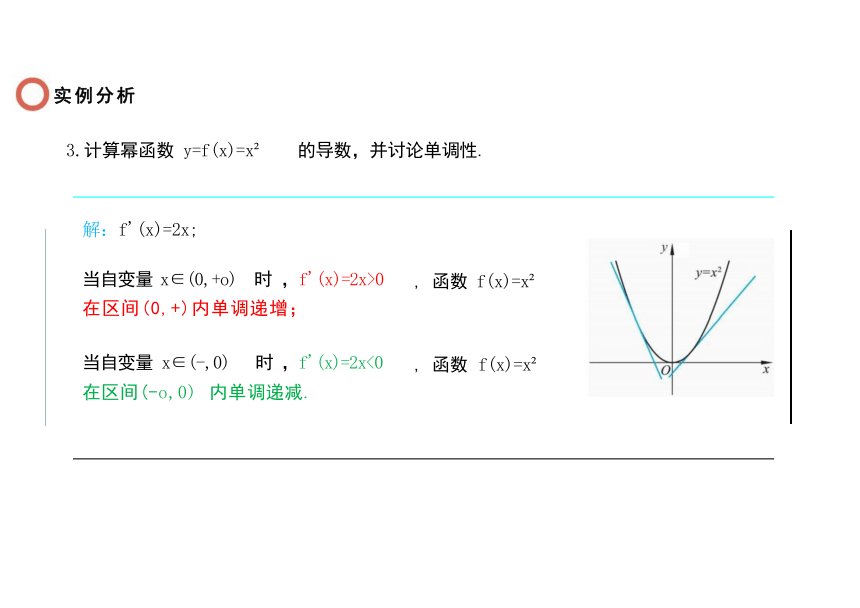
解:f'(x)=2x;
当自变量 x∈(0,+o) 时 ,f'(x)=2x>0 在区间(0,+)内单调递增;
, 函数 f(x)=x
当自变量 x∈(-,0) 时 ,f'(x)=2x<0 在区间(-o,0) 内单调递减.
, 函数 f(x)=x
实例分析
3.计算幂函数 y=f(x)=x 的导数,并讨论单调性.
(1)若在某个区间内,函数y=f(x) 的导数f'(x)>0 , 则在这个区间内 , 函 数y=f(x) 单调递增;
(2)若在某个区间内,函数y=f(x) 的导数f'(x)<0 ,则在这个区间内 , 函 数y=f(x) 单调递减.
注意:若在某个区间内,f'(x)≥0 且只在有限个点为0,则在这个区间内,
函数 y=f(x) 单调递增;若在某个区间内,f'(x)≤0 , 且只在有限个点为0, 则在这个区间内,函数y=f(x) 单调递减.
抽象概括
导数的符号与函数的单调性之间具有如下的关系:
解:f'(x)=6x -6x-36=6(x+2)(x-3)
设f'(x)>0, 则 6(x+2)(x-3)>0, 即 x<-2 或 x>3.
故当x∈(-0,-2) 或 x∈(3,+0) 时 ,f'(x)>0, 因此,在这两个区间上,函
数 f(x)均单调递增;
当x∈(-2,3) 时 ,f'(x)<0, 因此,在这个区间上,函数f(x)单调递减.
例1讨论函数f(x)=2x -3x -36x+16
的单调性.
例题分析
函数的单调性决定了函数图像的大致形状.
因此,当确定了函数的单调性后,再通过描出一
些特殊的点,如(-2,60),(3,-65)等,就可以画 出函数的大致图像.右图即为 f(x)=2x -3x -
36x+16 的大致图像.
思 考 交 流
你能画出 f(x)=2x -3x -36x+16 的大致图像吗
判断函数y=f(x) 的单调性的步骤:
(1)确定函数的定义域;
(2)求出导数f'(x)的零点;
(3)用f'(x)的零点将f(x)的定义域划分为若干个区间,列表给出f'(x) 在各区间上的正负,由此得出函数y=f(x) 在定义域内的单调性.
抽象概括
抽象概括
知识剖析
(1)定义域优先原则:函数的单调区间必须在函数的定义域内,因此, 在利用导数讨论函数的单调性时,必须结合函数的定义域.
(2)注意“临界点”和“间断点”:对函数划分单调区间时,除了必须确定使导数等 于零的点外,还要注意“间断点”.
如分段函数 中 x=0 就是间断点.
(3)区间的端点可以属于单调区间,也可以不属于单调区间, 一般情况 下,可将单调区间取为开区间.
(4)为了简便,有时可以省去列表这一步骤,直接解不等式f'(x)>0 得到 函数的单调递增区间,解不等式f'(x)<0 得到函数的单调递减区间.
抽象概括
知识剖析
当 堂 检 测
解 析 :由题意,得函数f(x)的定义域为(0,+0), 由f'x)<0及x>0,得
故函数f(x)的单调递减区间是
当堂检测
1.函数 的单调递减区间是 (
A. B. D.[0,1]
2.已 知 函 数y=xf'(x) 的图象如图所示(其中f'(x) 是函数f(x) 的导函数),则下面四个图象中, y=f(x)
的图象大致是( )
B..
当 堂 检 测
C.
A.
D.
解析: 由题中函数y=xf'(x) 的图象,可得
当x<-1 时 ,xf'(x)<0, 则 f'(x)>0,f(x) 单调递增;
当 - 10, 则 f'(x)<0,f(x) 单调递减;
当 0当x>1 时 ,xf'(x)>0, 则 f'(x)>0,f(x) 单调递增.
综上, f(x) 单调递增区间为(-,-1),(1,+0),单调递减区间为(-1,1).故选 C.
当堂检测
解析:
因为函数 在R 上为单调函数,所以f'(x)不存在变号零点,
即ax -2ax+1=0 在 R 上有一个根或0个根.当a=0 时,满足题意;
当a≠0 时,需满足(-2a) -4a,,0, 即 0当堂检测
3.若函数 在R 上为单调函数,则实数a 的取值范围是(D
A.(1,+0) B.[-1,0] C.[0,1] D.[0,1]
A. B. c D. 解 析 :因为函数f(x)=m+x -xlnx为“1阶比增函数”, 在(0,+o)上为增函数令 …0在(0,+0)上恒成立,所以m,,x -x在 xe(0,+o)上恒成立,由于当x∈(0,+o)时,
所以
当堂检测
4.已知函数f(x)的定义域为(0,+0),若 在(0,+o)上为增函数,则称f(x)为“k
阶比增函数".若函数f(x)=m+x -xlnx 为“1阶比增函数”,则实数m 的取值范围是 (
所以函数
, 得
由 f'(x)>0, 得x>e, 故 f(x)在区间(e,+0)上是增函数, 又 于是 即 b(e,+0),a,b,c 的大小关系为b 当堂检测
5.已知函数
则该函数的单调递增区间为
解析:(1) f'(x)=(2x+2)e -(x +2x)e =-(x -2)e .
令 f'(x)>0, 得- √2令 f'(x)<0, 得x<- √2 或x> √2,
故函数f(x)的单调递减区间为[-,- √2],[ √2,+o), 单调递增区间为[- √2, √2].
当堂检测
6.求下列函数的单调区间.
(1)f(x)=(x +2x)e*;(2)
(3)f(x)=e*+ax-1(a 为常数).
解析:(2)
即 ), 即 故函数f(x)的单调递增区间为 (keZ), 单调递减区间为
当堂检测
6.求下列函数的单调区间.
(1)f(x)=(x +2x)e*;(2)
令f'(x)>0,得
令f'(x)<0,得
(3)f(x)=e*+ax-1(a 为常数).
(keZ).
,
解析:(3) f'(x)=e*+a, 当a..0 时 ,f'(x)>0 恒成立,所以f(x)在 R 上单调递增.
当 a<0 时,令f'(x)>0, 得x>In(-a), 令 f'(x)<0, 得 x所 以f(x) 在(ln(-a),+0) 上单调递增,在(-○0,In(-a)] 上单调递减.
综上,当a….0 时 ,f(x) 在 R 上单调递增;当a<0 时 ,f(x) 在[ln(-a),+00] 上单调递增, 在(-○,ln(-a)) 上单调递减.
当堂检测
6.求下列函数的单调区间.
(1)f(x)=(x +2x)e*;(2)
(3)f(x)=e*+ax-1(a 为常数) .
利用导数研究含参函 数f(x) 的单调区间的一般步骤
(1) 确定函数f(x) 的定义域;
(2) 求导数f'(x);
(3) 分析参数对区间端点、最高次项的系数的影响,以及不等式解集的端 点与定义域的关系,恰当确定参数的不同范围,并进行分类讨论;
(4) 在不同的参数范围内,解不等式f'(x)>0 和 f'(x)<0, 确定函数f(x) 的单调区间.
方法总结
2.6.1函数的单调性
北师大版(2019)选择性必修第二册
第二章导数及其应用
学习目标
理解导数与函数的单调性的关系.
掌握利用导数判断函数单调性的方法.
会用导数求函数的单调区间.
同学们,我们之前简单学习了函数的单调性, 一起回顾一下.
一般地,设函数f(x) 的定义域为I, 如果对于定义域I 内某个
区间 D 上的任意两个自变量的值x ,x ,
当x
当x
减函数;
如果函数y=f(x) 在区间D 上是增函数或减函数,那么就说函数
y=f(x) 在这一区间具有单调性.区间D 叫做函数的单调区间.
知 识 回 顾
在数学中,称函数y=f(x) 在点xo 的瞬时变化率为该函数在点x。处的导数,通常用符
号f'(xo) 表示,记作
L
个y
A
P
X x
个V
P
A
可 X x
知识回顾
导数的概念
……
问题提出
我们知道,对于函数y=f(x) 来说,导数f'(x)刻画的是函数y=f(x)
在点x 的瞬时变化率,函数的单调性描述的是函数值y 随自变量x 取值 的增加而增加,或函数值y 随自变量x 取值的增加而减少.
两者都在刻画函数的变化,那么,导数与函数的单调性之间有何关系
呢
解: (1) f'(x)=1;(2)f'(x)=2;(3)f'(x)=-3 函数(1)(2)的导数都是正的,在定义域(-0,+0)内 函数值都是随x 的增加而增加的; 函数(3)的导数是负的,在定义域(-o,+o) 内函数 值是随x 的增加而减少的. y ,y=2x+5 y=x 0 y=-3x+4
X
实例分析
1.计算下面几个一次函数的导数,并讨论它们的单调性.
(1)y=f(x)=x (2)y=f(x)=2x+5 (3)y=f(x)=-3x+4
(1) (2) (3) (4)
对于函数(1)和(3),相应的定义域内的每一个x 都满足f'(x)>0
函数y=f(x) 在其定义域内是增函数;
对于函数(2)和(4),相应的定义域内的每一个x 都满足f'(x)<0,
函数y=f(x) 在其定义域内是减函数.
2.计算下列指数函数、对数函数的导数,并讨论它们的单调性.
(1)y=f(x)=2×
(3)y=f(x)=log x (4)
解:(1)f'(x)=2×In2;
实例分析
(2)
(3)
解:f'(x)=2x;
当自变量 x∈(0,+o) 时 ,f'(x)=2x>0 在区间(0,+)内单调递增;
, 函数 f(x)=x
当自变量 x∈(-,0) 时 ,f'(x)=2x<0 在区间(-o,0) 内单调递减.
, 函数 f(x)=x
实例分析
3.计算幂函数 y=f(x)=x 的导数,并讨论单调性.
(1)若在某个区间内,函数y=f(x) 的导数f'(x)>0 , 则在这个区间内 , 函 数y=f(x) 单调递增;
(2)若在某个区间内,函数y=f(x) 的导数f'(x)<0 ,则在这个区间内 , 函 数y=f(x) 单调递减.
注意:若在某个区间内,f'(x)≥0 且只在有限个点为0,则在这个区间内,
函数 y=f(x) 单调递增;若在某个区间内,f'(x)≤0 , 且只在有限个点为0, 则在这个区间内,函数y=f(x) 单调递减.
抽象概括
导数的符号与函数的单调性之间具有如下的关系:
解:f'(x)=6x -6x-36=6(x+2)(x-3)
设f'(x)>0, 则 6(x+2)(x-3)>0, 即 x<-2 或 x>3.
故当x∈(-0,-2) 或 x∈(3,+0) 时 ,f'(x)>0, 因此,在这两个区间上,函
数 f(x)均单调递增;
当x∈(-2,3) 时 ,f'(x)<0, 因此,在这个区间上,函数f(x)单调递减.
例1讨论函数f(x)=2x -3x -36x+16
的单调性.
例题分析
函数的单调性决定了函数图像的大致形状.
因此,当确定了函数的单调性后,再通过描出一
些特殊的点,如(-2,60),(3,-65)等,就可以画 出函数的大致图像.右图即为 f(x)=2x -3x -
36x+16 的大致图像.
思 考 交 流
你能画出 f(x)=2x -3x -36x+16 的大致图像吗
判断函数y=f(x) 的单调性的步骤:
(1)确定函数的定义域;
(2)求出导数f'(x)的零点;
(3)用f'(x)的零点将f(x)的定义域划分为若干个区间,列表给出f'(x) 在各区间上的正负,由此得出函数y=f(x) 在定义域内的单调性.
抽象概括
抽象概括
知识剖析
(1)定义域优先原则:函数的单调区间必须在函数的定义域内,因此, 在利用导数讨论函数的单调性时,必须结合函数的定义域.
(2)注意“临界点”和“间断点”:对函数划分单调区间时,除了必须确定使导数等 于零的点外,还要注意“间断点”.
如分段函数 中 x=0 就是间断点.
(3)区间的端点可以属于单调区间,也可以不属于单调区间, 一般情况 下,可将单调区间取为开区间.
(4)为了简便,有时可以省去列表这一步骤,直接解不等式f'(x)>0 得到 函数的单调递增区间,解不等式f'(x)<0 得到函数的单调递减区间.
抽象概括
知识剖析
当 堂 检 测
解 析 :由题意,得函数f(x)的定义域为(0,+0), 由f'x)<0及x>0,得
故函数f(x)的单调递减区间是
当堂检测
1.函数 的单调递减区间是 (
A. B. D.[0,1]
2.已 知 函 数y=xf'(x) 的图象如图所示(其中f'(x) 是函数f(x) 的导函数),则下面四个图象中, y=f(x)
的图象大致是( )
B..
当 堂 检 测
C.
A.
D.
解析: 由题中函数y=xf'(x) 的图象,可得
当x<-1 时 ,xf'(x)<0, 则 f'(x)>0,f(x) 单调递增;
当 - 1
当 0
综上, f(x) 单调递增区间为(-,-1),(1,+0),单调递减区间为(-1,1).故选 C.
当堂检测
解析:
因为函数 在R 上为单调函数,所以f'(x)不存在变号零点,
即ax -2ax+1=0 在 R 上有一个根或0个根.当a=0 时,满足题意;
当a≠0 时,需满足(-2a) -4a,,0, 即 0
3.若函数 在R 上为单调函数,则实数a 的取值范围是(D
A.(1,+0) B.[-1,0] C.[0,1] D.[0,1]
A. B. c D. 解 析 :因为函数f(x)=m+x -xlnx为“1阶比增函数”, 在(0,+o)上为增函数令 …0在(0,+0)上恒成立,所以m,,x -x在 xe(0,+o)上恒成立,由于当x∈(0,+o)时,
所以
当堂检测
4.已知函数f(x)的定义域为(0,+0),若 在(0,+o)上为增函数,则称f(x)为“k
阶比增函数".若函数f(x)=m+x -xlnx 为“1阶比增函数”,则实数m 的取值范围是 (
所以函数
, 得
由 f'(x)>0, 得x>e, 故 f(x)在区间(e,+0)上是增函数, 又 于是 即 b
5.已知函数
则该函数的单调递增区间为
解析:(1) f'(x)=(2x+2)e -(x +2x)e =-(x -2)e .
令 f'(x)>0, 得- √2
故函数f(x)的单调递减区间为[-,- √2],[ √2,+o), 单调递增区间为[- √2, √2].
当堂检测
6.求下列函数的单调区间.
(1)f(x)=(x +2x)e*;(2)
(3)f(x)=e*+ax-1(a 为常数).
解析:(2)
即 ), 即 故函数f(x)的单调递增区间为 (keZ), 单调递减区间为
当堂检测
6.求下列函数的单调区间.
(1)f(x)=(x +2x)e*;(2)
令f'(x)>0,得
令f'(x)<0,得
(3)f(x)=e*+ax-1(a 为常数).
(keZ).
,
解析:(3) f'(x)=e*+a, 当a..0 时 ,f'(x)>0 恒成立,所以f(x)在 R 上单调递增.
当 a<0 时,令f'(x)>0, 得x>In(-a), 令 f'(x)<0, 得 x
综上,当a….0 时 ,f(x) 在 R 上单调递增;当a<0 时 ,f(x) 在[ln(-a),+00] 上单调递增, 在(-○,ln(-a)) 上单调递减.
当堂检测
6.求下列函数的单调区间.
(1)f(x)=(x +2x)e*;(2)
(3)f(x)=e*+ax-1(a 为常数) .
利用导数研究含参函 数f(x) 的单调区间的一般步骤
(1) 确定函数f(x) 的定义域;
(2) 求导数f'(x);
(3) 分析参数对区间端点、最高次项的系数的影响,以及不等式解集的端 点与定义域的关系,恰当确定参数的不同范围,并进行分类讨论;
(4) 在不同的参数范围内,解不等式f'(x)>0 和 f'(x)<0, 确定函数f(x) 的单调区间.
方法总结
同课章节目录
