2.2.1椭圆及其标准方程
图片预览






文档简介
课件26张PPT。
椭圆及其标准方程2.圆的定义是什么?我们是怎么画圆的?1.两点间的距离公式,若设A(x1,y1) B(x2,y2)则:|AB|=?在平面内,到定点的距离等于定长的点的轨迹。引入新课3.如果将圆的定义中的一个定点变成两个定 点,动点到定点距离的定长变成动点到两定点的距离之和为定长.那么,将会形成什么样 的轨迹曲线呢?引入新课 4.动手作图工 具: 纸板、细绳、图钉
作 法: 用图钉穿过准备好的细绳两端的套内,并把图钉固定在两个定点(两个定点间的距离小于绳长)上,然后用笔尖绷紧绳子,使笔尖慢慢移动,看画出的是什么样的一条曲线动画演示引入新课 平面内与两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫椭圆。两个定点F1、F2称为焦点,两焦点之间的距离称为焦距,记为2c。若设M为椭圆上的任意一点,则|MF1|+|MF2|=2a
注:定义中对“常数”加上了一个条件,即常数要大于|F1F2| (2a>2c,a>c>0)1、椭圆的定义注:这样规定是为了避免出现轨迹为一条线段或无任
何轨迹两种特殊情况,这一点非常重要。讲授新课xy 以F1、F2 所在直线为 x 轴,线段 F1F2
的垂直平分线为 y 轴建立直角坐标系.P( x , y )设 P( x,y )是椭圆上任意一点设|F1F2|=2c,则有F1(-c,0)、F2(c,0) 椭圆上的点满足|PF1 | + | PF2 |
为定值,设为2a,则2a>2c则:即:O方程:是椭圆的标准方程. 若以F1,F2所在的直线为y轴,
线段 F1F2的垂直平分线为x 轴建立
直角坐标系,推导出的方程又是怎
样的呢?方程:也是椭圆的标准方程.注:椭圆的焦点在坐标轴上,且两焦
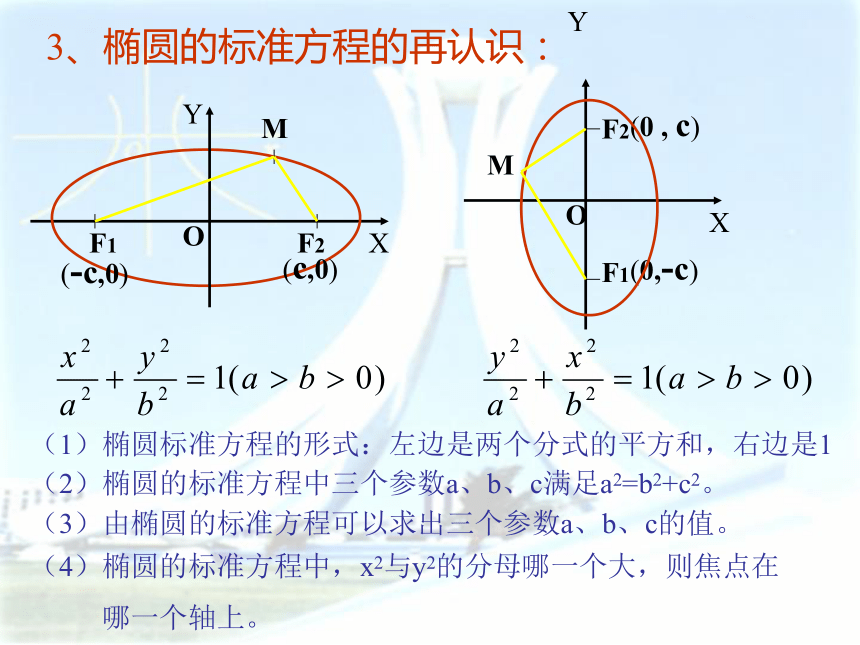
点的中点为坐标原点.2、椭圆标准方程的推导Y3、椭圆的标准方程的再认识:(1)椭圆标准方程的形式:左边是两个分式的平方和,右边是1(2)椭圆的标准方程中三个参数a、b、c满足a2=b2+c2。(3)由椭圆的标准方程可以求出三个参数a、b、c的值。(4)椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在
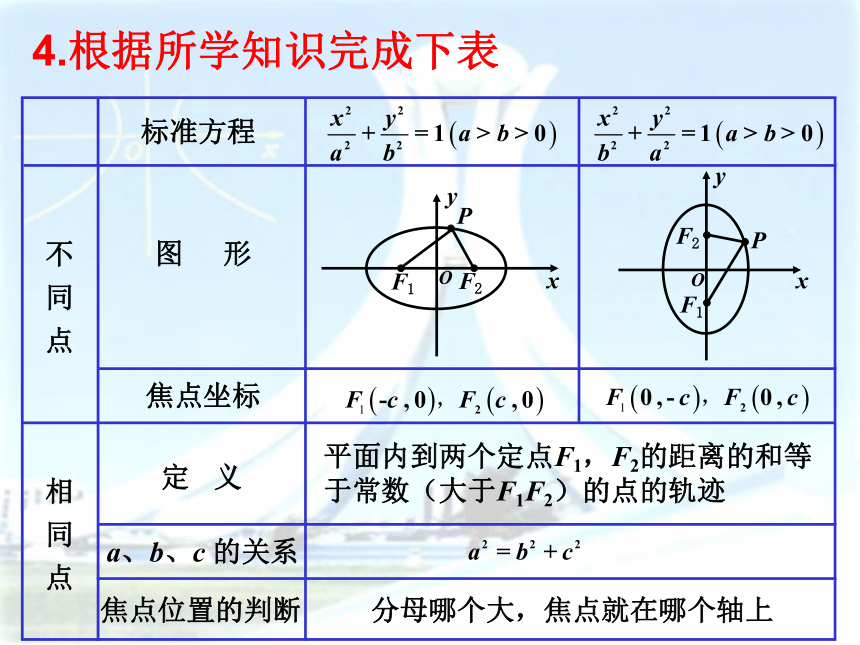
哪一个轴上。分母哪个大,焦点就在哪个轴上平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹4.根据所学知识完成下表快速反应534632变式练习题(一)变式练习题(二):判定下列椭圆的焦点在什么轴上,写出焦点坐标答:在 X 轴上,(-3,0)和(3,0)答:在 y 轴上,(0,-5)和(0,5)答:在y 轴上,(0,-1)和(0,1)判断椭圆标准方程的焦点在哪个轴上的准则:
x2与y2的分母哪一个大,则焦点在哪一个轴上。例1、填空:
(1)已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:____________焦距等于______;若CD为过左焦点F1的弦,则△F2CD的周长为________543(3,0)、(-3,0)6205、例题讲析(2)已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:___________焦距等于__________;曲线上一点P到左焦点F1的距离为3,则点P到另一个焦点F2的距离等于_________,则△F1PF2的周长为___________21(0,-1)、(0,1)2例2:已知a=4,b=3,求焦点分别在x、y轴上
的椭圆的标准方程.解:当焦点在 x 轴上的标准方程为当焦点在 y 轴上的标准方程为5、例题讲析变式练习题(三)
求满足下列条件的椭圆的标准方程:
(1)满足a=4,b=1,焦点在X轴上的椭圆的标准方程为____________ (2)满足a=4,c= ,焦点在Y轴上的椭圆的标准方程为____________ 求椭圆的标准方程需求几个量?答:两个;a、b 或 a、c 或 b、c;且满足 a2 = b2 + c2.“椭圆的标准方程”是个专有名词,就是指上述的两个方程,形式是固定的.思考:例3:已知椭圆的焦点坐标是F1(- 4,0),F2(4,0),
椭圆上的任意一点到F1,F2的距离之和是
10,求椭圆的标准方程.解:根据题意有焦点在 x 轴上,且 c = 4,2a = 10故椭圆的标准方程是5、例题讲析课堂小结思考:Ax2+By2=C中,A、B、C满足什么条件,就表示椭圆?答:当A、B、C 同号,且 A不等于B 时表示椭圆.作业:课后习题2.2
p49 1、2谢谢各位老师的指导再见!Or设圆上任意一点P(x,y) 以圆心O为原点,建立直角坐标系 两边平方,得 1.建系2.设坐标3.列等式坐标法 5.化简方程O
椭圆及其标准方程2.圆的定义是什么?我们是怎么画圆的?1.两点间的距离公式,若设A(x1,y1) B(x2,y2)则:|AB|=?在平面内,到定点的距离等于定长的点的轨迹。引入新课3.如果将圆的定义中的一个定点变成两个定 点,动点到定点距离的定长变成动点到两定点的距离之和为定长.那么,将会形成什么样 的轨迹曲线呢?引入新课 4.动手作图工 具: 纸板、细绳、图钉
作 法: 用图钉穿过准备好的细绳两端的套内,并把图钉固定在两个定点(两个定点间的距离小于绳长)上,然后用笔尖绷紧绳子,使笔尖慢慢移动,看画出的是什么样的一条曲线动画演示引入新课 平面内与两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫椭圆。两个定点F1、F2称为焦点,两焦点之间的距离称为焦距,记为2c。若设M为椭圆上的任意一点,则|MF1|+|MF2|=2a
注:定义中对“常数”加上了一个条件,即常数要大于|F1F2| (2a>2c,a>c>0)1、椭圆的定义注:这样规定是为了避免出现轨迹为一条线段或无任
何轨迹两种特殊情况,这一点非常重要。讲授新课xy 以F1、F2 所在直线为 x 轴,线段 F1F2
的垂直平分线为 y 轴建立直角坐标系.P( x , y )设 P( x,y )是椭圆上任意一点设|F1F2|=2c,则有F1(-c,0)、F2(c,0) 椭圆上的点满足|PF1 | + | PF2 |
为定值,设为2a,则2a>2c则:即:O方程:是椭圆的标准方程. 若以F1,F2所在的直线为y轴,
线段 F1F2的垂直平分线为x 轴建立
直角坐标系,推导出的方程又是怎
样的呢?方程:也是椭圆的标准方程.注:椭圆的焦点在坐标轴上,且两焦
点的中点为坐标原点.2、椭圆标准方程的推导Y3、椭圆的标准方程的再认识:(1)椭圆标准方程的形式:左边是两个分式的平方和,右边是1(2)椭圆的标准方程中三个参数a、b、c满足a2=b2+c2。(3)由椭圆的标准方程可以求出三个参数a、b、c的值。(4)椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在
哪一个轴上。分母哪个大,焦点就在哪个轴上平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹4.根据所学知识完成下表快速反应534632变式练习题(一)变式练习题(二):判定下列椭圆的焦点在什么轴上,写出焦点坐标答:在 X 轴上,(-3,0)和(3,0)答:在 y 轴上,(0,-5)和(0,5)答:在y 轴上,(0,-1)和(0,1)判断椭圆标准方程的焦点在哪个轴上的准则:
x2与y2的分母哪一个大,则焦点在哪一个轴上。例1、填空:
(1)已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:____________焦距等于______;若CD为过左焦点F1的弦,则△F2CD的周长为________543(3,0)、(-3,0)6205、例题讲析(2)已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:___________焦距等于__________;曲线上一点P到左焦点F1的距离为3,则点P到另一个焦点F2的距离等于_________,则△F1PF2的周长为___________21(0,-1)、(0,1)2例2:已知a=4,b=3,求焦点分别在x、y轴上
的椭圆的标准方程.解:当焦点在 x 轴上的标准方程为当焦点在 y 轴上的标准方程为5、例题讲析变式练习题(三)
求满足下列条件的椭圆的标准方程:
(1)满足a=4,b=1,焦点在X轴上的椭圆的标准方程为____________ (2)满足a=4,c= ,焦点在Y轴上的椭圆的标准方程为____________ 求椭圆的标准方程需求几个量?答:两个;a、b 或 a、c 或 b、c;且满足 a2 = b2 + c2.“椭圆的标准方程”是个专有名词,就是指上述的两个方程,形式是固定的.思考:例3:已知椭圆的焦点坐标是F1(- 4,0),F2(4,0),
椭圆上的任意一点到F1,F2的距离之和是
10,求椭圆的标准方程.解:根据题意有焦点在 x 轴上,且 c = 4,2a = 10故椭圆的标准方程是5、例题讲析课堂小结思考:Ax2+By2=C中,A、B、C满足什么条件,就表示椭圆?答:当A、B、C 同号,且 A不等于B 时表示椭圆.作业:课后习题2.2
p49 1、2谢谢各位老师的指导再见!Or设圆上任意一点P(x,y) 以圆心O为原点,建立直角坐标系 两边平方,得 1.建系2.设坐标3.列等式坐标法 5.化简方程O
