2025年中考数学二轮复习-专题12与圆切线相关的计算证明【课件】(共47张PPT)
文档属性
| 名称 | 2025年中考数学二轮复习-专题12与圆切线相关的计算证明【课件】(共47张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 12:29:18 | ||
图片预览







文档简介
(共47张PPT)
专题十二 与圆切线相关的计算证明
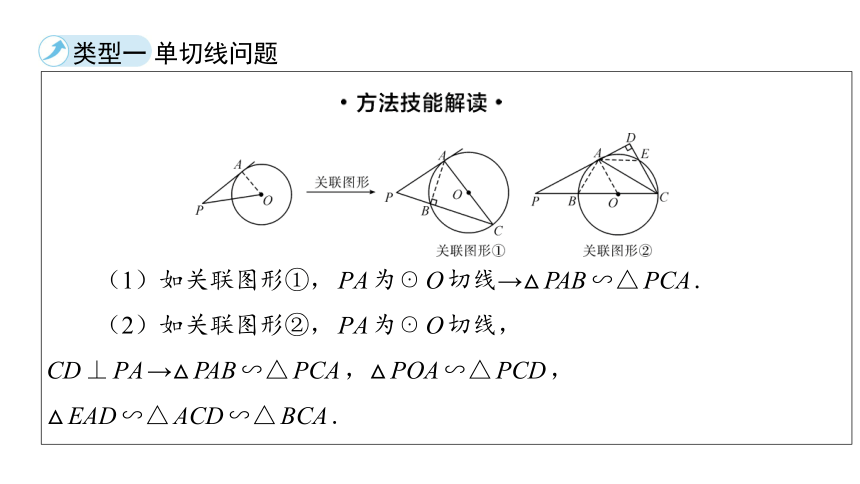
类型一 单切线问题
(1)如关联图形①,PA为☉O切线→△PAB∽△PCA.
(2)如关联图形②,PA为☉O切线,
CD⊥PA→△PAB∽△PCA,△POA∽△PCD,
△EAD∽△ACD∽△BCA.
1. 如图,AB是☉O的直径,直线DE是☉O的切线,切点为C,连接
AC. 若AC=5,tan∠ACE= ,则☉O的半径为 .
2. [2024·凉山州]如图,☉M的圆心为M(4,0),半径为2,P为直线
y=x+4上一个动点,过点P作☉M的切线,切点为Q,则PQ的最小值
为 .
2
3. 如图,在Rt△ABC中,∠B=90°,D为AC上一点,以CD为直径
的☉O与边AB相切于点E,连接DE. 若∠A=30°,则 的值
是 .
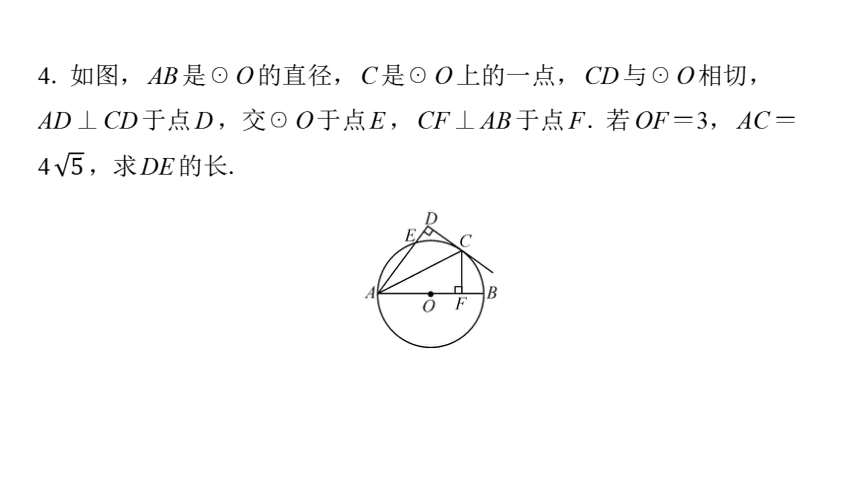
4. 如图,AB是☉O的直径,C是☉O上的一点,CD与☉O相切,
AD⊥CD于点D,交☉O于点E,CF⊥AB于点F. 若OF=3,AC=
4 ,求DE的长.
解:如图,连接OC,过点O作OG⊥AE于点G. 设☉O的半径为r.
∵CD与☉O相切,AD⊥CD,∴∠OCD=∠D=∠OGD=90°,
∴四边形OCDG为矩形,∴∠GOC=90°,GD=OC,
∴∠AOG+∠COF=90°.又∵∠OCF+∠COF=90°,
∴∠AOG=∠OCF. 又∵∠AGO=∠OFC=90°,AO=OC,
∴△AOG≌△OCF(AAS),∴EG=AG=OF=3.
∵CF2=AC2-AF2=OC2-OF2,∴ -(r+3)
2=r2-32,解得r1=5,r2=-8(舍去),
∴GD=OC=5,DE=GD-EG=5-3=2.
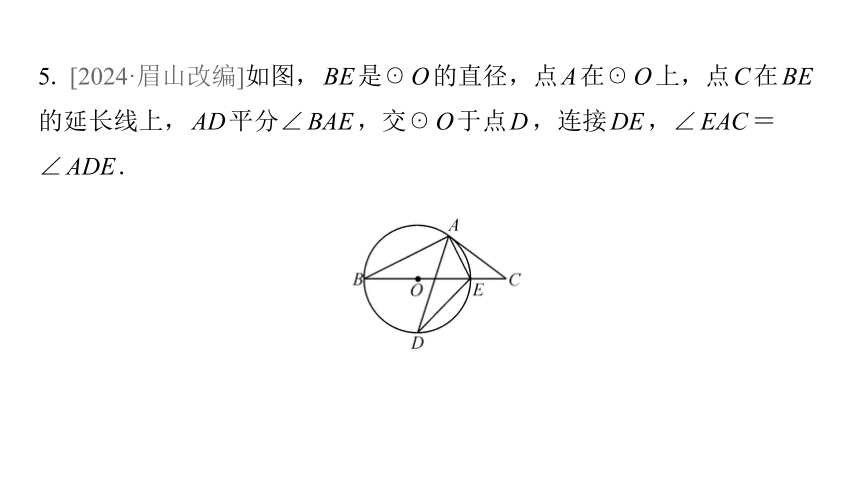
5. [2024·眉山改编]如图,BE是☉O的直径,点A在☉O上,点C在BE
的延长线上,AD平分∠BAE,交☉O于点D,连接DE,∠EAC=
∠ADE.
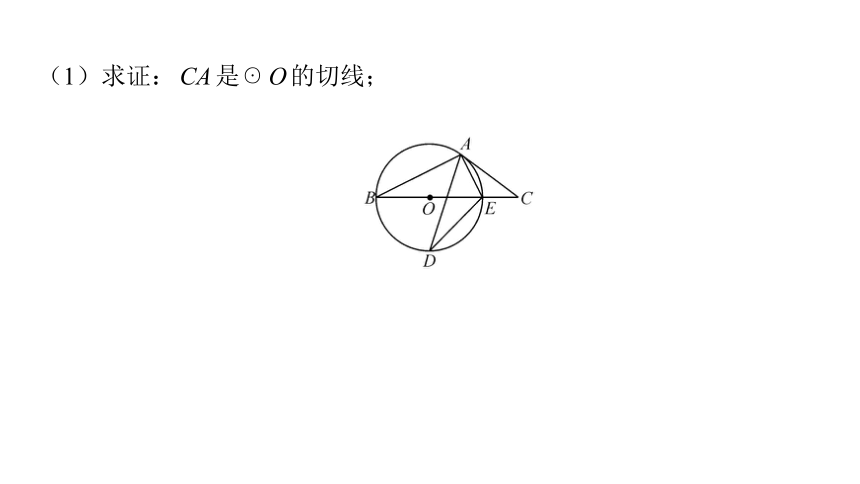
(1)求证:CA是☉O的切线;
(1)证明:如图,连接OA.
∵OA=OB,∴∠ABO=∠BAO.
又∵∠EAC=∠ADE=∠ABE,∴∠BAO=∠EAC.
∵BE为直径,∴∠BAE=∠BAO+∠OAE=90°,
∴∠OAC=∠EAC+∠OAE=∠BAO+∠OAE=90°,
∴OA⊥AC,∴CA是☉O的切线.
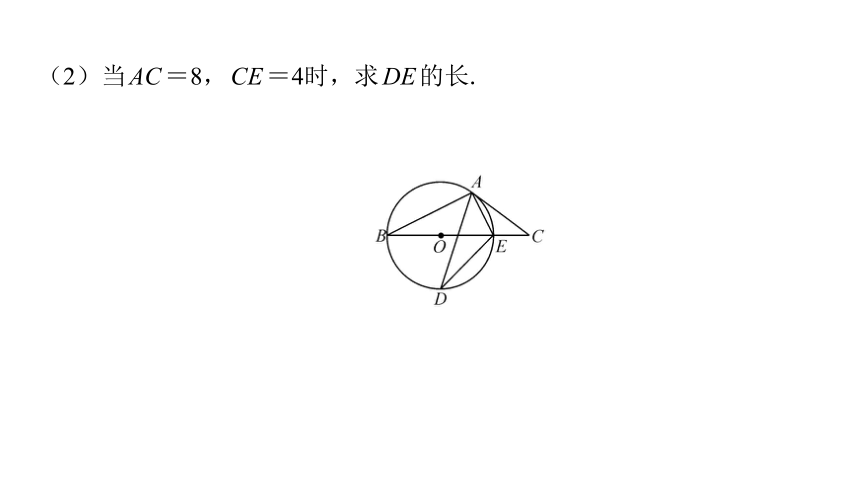
(2)当AC=8,CE=4时,求DE的长.
(2)解:如图,连接BD.
∵∠EAC=∠ABC,∠C=∠C,∴△ABC∽△EAC,
∴ = ,
即 = ,解得BC=16,∴BE=BC-CE=12.
∵AD平分∠BAE,∴ = ,∴BD=ED. 又∵∠BDE=90°,
∴△BDE是等腰直角三角形,∴DE=BD= BE= ×12=6 .
6. 如图,以AB为直径的☉O上有两点E,F, = ,过点E作直
线CD⊥AF,交AF的延长线于点D,交AB的延长线于点C,过点C作
CM平分∠ACD,交AE于点M,交BE于点N.
(1)求证:CD是☉O的切线;
(1)证明:如图,连接OE.
∵ = ,∴∠EAF=∠EAB. ∵OA=OE,
∴∠OEA=∠EAB,
∴∠OEA=∠EAF,∴OE∥AD. 又∵AD⊥CD,
∴OE⊥CD,∴CD是☉O的切线.
(2)求证:EM=EN;
(2)证明:∵OE⊥CD,∴∠OEB+∠BEC=90°.∵AB为直径,
∴∠EAB+∠OBE=90°.
∵OE=OB,∴∠OEB=∠OBE,∴∠BEC=∠EAB. 又∵CM平分
∠ACD,∴∠MCA=∠NCE,
∵∠EMN=∠MAC+∠MCA,∠ENM=∠NEC+∠NCE,
∴∠EMN=∠ENM,∴EM=EN.
(3)若N是CM的中点,且AB=9 ,求EN的长.
(3)解:∵N是CM的中点,∴CM=2CN.
∵∠CEN=∠CAM,∠ECN=∠ACM,∴△CEN∽△CAM,∴ =
= = .
∵∠CEB=∠CAE,∠ECB=∠ACE,∴△CEB∽△CAE,∴ =
= .
设EN=x,则EM=EN=x,AM=2EN=2x,AE=3x,EB= AE
= x,
∴AE2+EB2=AB2,∴(3x)2+ = ,解得x1=6,
x2=-6(舍去),∴EN的长为6.
类型二 双切线问题
如图,PA,PB为☉O的两条切线,该图形经常与“等腰三角形三
线合一”“垂径定理”的结构图形关联使用.
(1)如关联图形①,PA,PB为☉O切线→△OCA∽△PCB.
(2)如关联图形②,PA,PB为☉O切线→P为BC的中点,OP
为△BCD的中位线,△PAB∽△OAD.
1. 如图,在Rt△ABC中,∠ABC=90°,AC=13,AB=12,D为AB
的中点.若以CD上的一点O为圆心作☉O,恰好与AB,AC都相切,则
☉O的半径为 .
2. 如图,PA,PB分别与☉O相切于点A,B,连接AO并延长,交PB
的延长线于点C. 若OA=3,OC=5,则PB的长为 .
6
3. 如图,在Rt△ABC中,∠ACB=90°,点O在BC上,以OC为半径
的☉O与AB相切于点E,与OB交于点D. 若BD=1,tan∠AOC=2,
则☉O的面积是 .
π
4. 如图,在Rt△ABC中,∠BAC=90°,点O 在边AB上,以O为圆
心,OA长为半径的☉O交AB于另一点E,与BC相切于点D,CE交
☉O于点F. 若☉O的半径为3,BD=4,则EF的长为 .
3
5. 如图,CA,CD是☉O的两条切线,切点分别为A,D,AB是☉O
的切线,AB=AC,AF⊥CD于点F,交☉O于点E. 若AB=2,求AE
的长.
解:如图,连接BE,OD,OD交BE于点G.
易得四边形EFDG为矩形,OD垂直平分BE,
△ABE≌△CAF(AAS).
设AE=CF=x,则GE=DF=2-x,BE=2GE=4-2x.
∵AB2=AE2+BE2,∴22=x2+(4-2x)2,
解得x1= ,x2=2(舍去),∴AE的长为 .
6. 如图,PA,PB分别与☉O 相切于点A,B,AC是☉O的直径.已知
tan∠ACB= ,求tan∠PCB的值.
解:如图,连接AB,OP. 设AB与OP,PC分别交于点M,N.
∵PA,PB分别与☉O 相切于点A,B,∴OP⊥AB,AM=BM.
又∵AC是☉O的直径,∴BC⊥AB,∴BC∥OP,OM为△ABC的中位线,
∴tan∠AOM=tan∠ACB= = .
设AM= k,OM=k,则BM= k,BC=2k.易得△AOM∽△PAM,
∴AM2=OM·PM,∴ =k×PM,∴PM=5k.∵BC∥OP,∴△PMN∽△CBN,
∴ = = = ,∴MN= MB= k,
∴tan∠PCB=tan∠MPN= = = .
7. 如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为
半径的圆交AC于点D,E是BC的中点,连接DE,OC.
(1)判断DE与☉O的位置关系,并说明理由;
解:(1)DE与☉O相切.理由如下:
如图,连接OD,OE. ∵O,E分别为AB,BC的中点,∴OE为
△ABC的中位线,
∴OE∥AC,∴∠BOE=∠OAD=∠ODA=∠DOE. 又∵OD=
OB,OE=OE,
∴△OBE≌△ODE(SAS),∴∠ODE=∠OBE=90°,
∴OD⊥DE,∴DE与☉O相切.
(2)OC交DE于点F,若 cos ∠BAD= ,求 的值.
(2)如图,连接BD,则 cos ∠BAD= = .
设AD=3a,AB=5a.∵ cos ∠BAD= = = ,∴AC= ,
∴OE= AC= ,CD=AC-AD= .又∵OE∥CD,∴ =
= = .
类型三 多切线问题
(1)如关联图形①,AD,BC,CD为☉O切线→△OCD为直角
三角形,CD=BC+AD,△OBC∽△DOC∽△DAO.
(2)如关联图形②,PA,PB,MN为☉O切线→△PMN的周长
为2PA,点O为△PMN外角平分线的交点.
1. 如图,☉O与四边形ABCD的各边都相切,若AB=13,CD=5,
☉O的半径为4,则四边形ABCD的面积是 .
72
2. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,☉O 为
△ABC的内切圆,D,E,F为切点,DE交BC的延长线于点M,则
EM的长为 .
2
3. 如图,已知直角梯形ABCD,AD=1,BC=4,以AB为直径的☉O
切CD于点E,连接AE,则 sin ∠AED的值为 .
4. 如图,等腰三角形ABC的内切圆☉O与AB,BC,CA分别相切于点
D,E,F. 若AB=AC=5,BC=6,则DE的长为 .
5. 如图,已知☉O的半径为r,PA,PB分别切☉O于A,B两点,CD
切☉O于点E,交PA,PB于点C,D. 若△PCD的周长为3r,求
tan∠APB的值.
解:如图,连接OA,OB,延长AO,PB相交于点F.
∵△PCD的周长为3r,∴PA=PB=1.5r.
易得△BFO∽△AFP,∴ = = = .设BF=2a,AF=3a.
在Rt△OBF中,(3a-r)2=r2+(2a)2,∴a= r,
∴tan∠APB= = = = .
6. 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,以B为圆
心,BA为半径的圆与CD相切于点E,交BC于点F,过点F作☉B的切
线,交CD于点M. 若AD=4,FM=6,求BC的长.
解:如图,延长AD,FM相交于点N,连接BD. 由切线长定理可得
ED=AD=4,EM=FM=6,
∴DM=10.
易得四边形ABFN为正方形.设正方形ABFN的边长为a,
则DN=a-4,MN=a-6.
∵DN2+MN2=DM2,∴(a-4)2+(a-6)2=102,
解得a1=12,a2=-2(舍去),
∴FN=12,FM=NM=6.又∵∠N=∠MFC,
∠DMN=∠CMF,∴△DMN≌△CMF,
∴CM=DM=10,DC=20.又∵∠CDB=∠ADB=
∠CBD,∴BC=DC=20.
谢谢观看
专题十二 与圆切线相关的计算证明
类型一 单切线问题
(1)如关联图形①,PA为☉O切线→△PAB∽△PCA.
(2)如关联图形②,PA为☉O切线,
CD⊥PA→△PAB∽△PCA,△POA∽△PCD,
△EAD∽△ACD∽△BCA.
1. 如图,AB是☉O的直径,直线DE是☉O的切线,切点为C,连接
AC. 若AC=5,tan∠ACE= ,则☉O的半径为 .
2. [2024·凉山州]如图,☉M的圆心为M(4,0),半径为2,P为直线
y=x+4上一个动点,过点P作☉M的切线,切点为Q,则PQ的最小值
为 .
2
3. 如图,在Rt△ABC中,∠B=90°,D为AC上一点,以CD为直径
的☉O与边AB相切于点E,连接DE. 若∠A=30°,则 的值
是 .
4. 如图,AB是☉O的直径,C是☉O上的一点,CD与☉O相切,
AD⊥CD于点D,交☉O于点E,CF⊥AB于点F. 若OF=3,AC=
4 ,求DE的长.
解:如图,连接OC,过点O作OG⊥AE于点G. 设☉O的半径为r.
∵CD与☉O相切,AD⊥CD,∴∠OCD=∠D=∠OGD=90°,
∴四边形OCDG为矩形,∴∠GOC=90°,GD=OC,
∴∠AOG+∠COF=90°.又∵∠OCF+∠COF=90°,
∴∠AOG=∠OCF. 又∵∠AGO=∠OFC=90°,AO=OC,
∴△AOG≌△OCF(AAS),∴EG=AG=OF=3.
∵CF2=AC2-AF2=OC2-OF2,∴ -(r+3)
2=r2-32,解得r1=5,r2=-8(舍去),
∴GD=OC=5,DE=GD-EG=5-3=2.
5. [2024·眉山改编]如图,BE是☉O的直径,点A在☉O上,点C在BE
的延长线上,AD平分∠BAE,交☉O于点D,连接DE,∠EAC=
∠ADE.
(1)求证:CA是☉O的切线;
(1)证明:如图,连接OA.
∵OA=OB,∴∠ABO=∠BAO.
又∵∠EAC=∠ADE=∠ABE,∴∠BAO=∠EAC.
∵BE为直径,∴∠BAE=∠BAO+∠OAE=90°,
∴∠OAC=∠EAC+∠OAE=∠BAO+∠OAE=90°,
∴OA⊥AC,∴CA是☉O的切线.
(2)当AC=8,CE=4时,求DE的长.
(2)解:如图,连接BD.
∵∠EAC=∠ABC,∠C=∠C,∴△ABC∽△EAC,
∴ = ,
即 = ,解得BC=16,∴BE=BC-CE=12.
∵AD平分∠BAE,∴ = ,∴BD=ED. 又∵∠BDE=90°,
∴△BDE是等腰直角三角形,∴DE=BD= BE= ×12=6 .
6. 如图,以AB为直径的☉O上有两点E,F, = ,过点E作直
线CD⊥AF,交AF的延长线于点D,交AB的延长线于点C,过点C作
CM平分∠ACD,交AE于点M,交BE于点N.
(1)求证:CD是☉O的切线;
(1)证明:如图,连接OE.
∵ = ,∴∠EAF=∠EAB. ∵OA=OE,
∴∠OEA=∠EAB,
∴∠OEA=∠EAF,∴OE∥AD. 又∵AD⊥CD,
∴OE⊥CD,∴CD是☉O的切线.
(2)求证:EM=EN;
(2)证明:∵OE⊥CD,∴∠OEB+∠BEC=90°.∵AB为直径,
∴∠EAB+∠OBE=90°.
∵OE=OB,∴∠OEB=∠OBE,∴∠BEC=∠EAB. 又∵CM平分
∠ACD,∴∠MCA=∠NCE,
∵∠EMN=∠MAC+∠MCA,∠ENM=∠NEC+∠NCE,
∴∠EMN=∠ENM,∴EM=EN.
(3)若N是CM的中点,且AB=9 ,求EN的长.
(3)解:∵N是CM的中点,∴CM=2CN.
∵∠CEN=∠CAM,∠ECN=∠ACM,∴△CEN∽△CAM,∴ =
= = .
∵∠CEB=∠CAE,∠ECB=∠ACE,∴△CEB∽△CAE,∴ =
= .
设EN=x,则EM=EN=x,AM=2EN=2x,AE=3x,EB= AE
= x,
∴AE2+EB2=AB2,∴(3x)2+ = ,解得x1=6,
x2=-6(舍去),∴EN的长为6.
类型二 双切线问题
如图,PA,PB为☉O的两条切线,该图形经常与“等腰三角形三
线合一”“垂径定理”的结构图形关联使用.
(1)如关联图形①,PA,PB为☉O切线→△OCA∽△PCB.
(2)如关联图形②,PA,PB为☉O切线→P为BC的中点,OP
为△BCD的中位线,△PAB∽△OAD.
1. 如图,在Rt△ABC中,∠ABC=90°,AC=13,AB=12,D为AB
的中点.若以CD上的一点O为圆心作☉O,恰好与AB,AC都相切,则
☉O的半径为 .
2. 如图,PA,PB分别与☉O相切于点A,B,连接AO并延长,交PB
的延长线于点C. 若OA=3,OC=5,则PB的长为 .
6
3. 如图,在Rt△ABC中,∠ACB=90°,点O在BC上,以OC为半径
的☉O与AB相切于点E,与OB交于点D. 若BD=1,tan∠AOC=2,
则☉O的面积是 .
π
4. 如图,在Rt△ABC中,∠BAC=90°,点O 在边AB上,以O为圆
心,OA长为半径的☉O交AB于另一点E,与BC相切于点D,CE交
☉O于点F. 若☉O的半径为3,BD=4,则EF的长为 .
3
5. 如图,CA,CD是☉O的两条切线,切点分别为A,D,AB是☉O
的切线,AB=AC,AF⊥CD于点F,交☉O于点E. 若AB=2,求AE
的长.
解:如图,连接BE,OD,OD交BE于点G.
易得四边形EFDG为矩形,OD垂直平分BE,
△ABE≌△CAF(AAS).
设AE=CF=x,则GE=DF=2-x,BE=2GE=4-2x.
∵AB2=AE2+BE2,∴22=x2+(4-2x)2,
解得x1= ,x2=2(舍去),∴AE的长为 .
6. 如图,PA,PB分别与☉O 相切于点A,B,AC是☉O的直径.已知
tan∠ACB= ,求tan∠PCB的值.
解:如图,连接AB,OP. 设AB与OP,PC分别交于点M,N.
∵PA,PB分别与☉O 相切于点A,B,∴OP⊥AB,AM=BM.
又∵AC是☉O的直径,∴BC⊥AB,∴BC∥OP,OM为△ABC的中位线,
∴tan∠AOM=tan∠ACB= = .
设AM= k,OM=k,则BM= k,BC=2k.易得△AOM∽△PAM,
∴AM2=OM·PM,∴ =k×PM,∴PM=5k.∵BC∥OP,∴△PMN∽△CBN,
∴ = = = ,∴MN= MB= k,
∴tan∠PCB=tan∠MPN= = = .
7. 如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为
半径的圆交AC于点D,E是BC的中点,连接DE,OC.
(1)判断DE与☉O的位置关系,并说明理由;
解:(1)DE与☉O相切.理由如下:
如图,连接OD,OE. ∵O,E分别为AB,BC的中点,∴OE为
△ABC的中位线,
∴OE∥AC,∴∠BOE=∠OAD=∠ODA=∠DOE. 又∵OD=
OB,OE=OE,
∴△OBE≌△ODE(SAS),∴∠ODE=∠OBE=90°,
∴OD⊥DE,∴DE与☉O相切.
(2)OC交DE于点F,若 cos ∠BAD= ,求 的值.
(2)如图,连接BD,则 cos ∠BAD= = .
设AD=3a,AB=5a.∵ cos ∠BAD= = = ,∴AC= ,
∴OE= AC= ,CD=AC-AD= .又∵OE∥CD,∴ =
= = .
类型三 多切线问题
(1)如关联图形①,AD,BC,CD为☉O切线→△OCD为直角
三角形,CD=BC+AD,△OBC∽△DOC∽△DAO.
(2)如关联图形②,PA,PB,MN为☉O切线→△PMN的周长
为2PA,点O为△PMN外角平分线的交点.
1. 如图,☉O与四边形ABCD的各边都相切,若AB=13,CD=5,
☉O的半径为4,则四边形ABCD的面积是 .
72
2. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,☉O 为
△ABC的内切圆,D,E,F为切点,DE交BC的延长线于点M,则
EM的长为 .
2
3. 如图,已知直角梯形ABCD,AD=1,BC=4,以AB为直径的☉O
切CD于点E,连接AE,则 sin ∠AED的值为 .
4. 如图,等腰三角形ABC的内切圆☉O与AB,BC,CA分别相切于点
D,E,F. 若AB=AC=5,BC=6,则DE的长为 .
5. 如图,已知☉O的半径为r,PA,PB分别切☉O于A,B两点,CD
切☉O于点E,交PA,PB于点C,D. 若△PCD的周长为3r,求
tan∠APB的值.
解:如图,连接OA,OB,延长AO,PB相交于点F.
∵△PCD的周长为3r,∴PA=PB=1.5r.
易得△BFO∽△AFP,∴ = = = .设BF=2a,AF=3a.
在Rt△OBF中,(3a-r)2=r2+(2a)2,∴a= r,
∴tan∠APB= = = = .
6. 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,以B为圆
心,BA为半径的圆与CD相切于点E,交BC于点F,过点F作☉B的切
线,交CD于点M. 若AD=4,FM=6,求BC的长.
解:如图,延长AD,FM相交于点N,连接BD. 由切线长定理可得
ED=AD=4,EM=FM=6,
∴DM=10.
易得四边形ABFN为正方形.设正方形ABFN的边长为a,
则DN=a-4,MN=a-6.
∵DN2+MN2=DM2,∴(a-4)2+(a-6)2=102,
解得a1=12,a2=-2(舍去),
∴FN=12,FM=NM=6.又∵∠N=∠MFC,
∠DMN=∠CMF,∴△DMN≌△CMF,
∴CM=DM=10,DC=20.又∵∠CDB=∠ADB=
∠CBD,∴BC=DC=20.
谢谢观看
同课章节目录
