2024-2025学年小升初数学备考真题分类汇编(四川地区专版)专题1 单项选择题(含解析)
文档属性
| 名称 | 2024-2025学年小升初数学备考真题分类汇编(四川地区专版)专题1 单项选择题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 357.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 07:34:45 | ||
图片预览



文档简介
专题1 选择题-2023-2024学年
小升初数学备考真题分类汇编(四川地区专版)
试卷说明:
本试卷试题精选自四川各市,县2024、2023近两年六年级下学期小升初期末真题试卷,难易度均衡,适合四川各市,县的六年级学生小升初择校考、分班考等复习备考使用!
一、单选题
1.(2024·北川)服装店售出的两件上衣都卖了120元。一件赚了20%,一件亏了20%。服装店在卖出这两件上衣时总体是( )
A.赚了 B.亏了 C.不赚不亏 D.无法确定
2.(2024·江阳)足球48元/个,杨老师要给学校足球队买198个足球,他大约要准备( )
A.8000元 B.10000元 C.100000元
3.(2024·朝天)下面式子中,a和b(a,b均不为0)成反比例关系的是( )
A.5a=4b B.= C.5a= D.5a=b+4
4.(2024·江阳)图中长方形和圆的面积相等,长方形的长是12.56cm,圆的面积是( )cm2。
A.50.24 B.25.12 C.12.56
5.(2024·达州)1.2:0.6可以和下面的( )组成一个比例。
A.: B.0.6:0.03 C.:0.8 D.12:0.06
6.(2024·朝天) 一个比的比值是,它的前项和后项都扩大到原来的3倍,这时比值是( )
A. B. C. D.
7.(2023·温江)淘气和笑笑玩掷骰子游戏,骰子各面上分别是1、2、3、4、5、6,下面( )
A.上面是奇数淘气胜,上面是偶数笑笑胜
B.上面是质数淘气胜,上面是合数笑笑胜
C.上面的数小于3淘气胜,上面的数大于3笑笑胜
D.上面的数小于4淘气胜,上面的数大于4笑笑胜
8.(2024·朝天)在带箭头的直线上表示下列各数,( )最接近0。
A.﹣2 B.3 C.﹣1 D.2.5
9.(2023·新都)一个圆柱与一个圆锥体积相等,底面积也相等。已知圆锥的高是12厘米,圆柱的高是( )厘米。
A.4 B.12 C.24 D.36
10.(2024·北川)星期天爸爸开车送小强去看电影,看完电影后,小强步行回家。下面能反映小强活动情况的是( )
A. B.
C. D.
11.(2024·北川)如下图,一个圆柱切拼成一个近似长方体后( )
A.表面积不变,体积不变。 B.表面积不变,体积变大。
C.表面积变大,体积不变。 D.表面积变大,体积变大。
12.(2024·北川)今年上半年的总天数是( )
A.180天 B.181天 C.182天 D.183天
13.(2024·北川)已知a>0,则下列各式中,得数最大的是( )
A.a×(1+) B.a×(1-) C.a÷(1+) D.a÷(1-)
14.(2024·北川)在一座桥梁旁,有一块限重的交通标志牌(如图),被污渍遮挡住的字母应当是( )
A.km B.Kg C.T D.L
15.(2023·叙永)一个圆柱与圆锥的体积相等,圆柱的半径与圆锥的半径相等,圆柱的高与圆锥的高的比是( )
A.3:1 B.1:3 C.9:1 D.1:9
16.(2024·北川) 一个圆柱形零件的高是5mm,画在图纸上的高是5cm。这幅图纸的比例尺是( )
A.1:1 B.10:1 C.1:10 D.10
17.(2024·北川)下面不能用百分数表示的是( )
A.折扣 B.成数 C.税率 D.利息
18.(2024·北川)用n表示自然数0、1、2、3、4、5、6……,表示奇数比较合适的是( )
A.n+1 B.n﹣1 C.2n+1 D.2n﹣1
19.(2024·朝天)式子×<1的□里可以填的最大整数是( )
A.4 B.5 C.6 D.7
20.(2024·朝天)手工课上老师给学生发折纸,有红、黄、蓝三种,每人发一种,如果这个班有37名学生,那么至少有( )名学生拿到相同颜色的折纸。
A.11 B.12 C.13 D.14
21.(2024·朝天)甜甜妈妈花了180元买了一双打六折的童鞋,这双童鞋的原价是( )元。
A.450 B.300 C.288 D.108
22.(2024·朝天) 一个长方形按3:1的比放大后,所得图形的面积与原图形的面积的比是( )
A.9:1 B.6:1 C.3:1 D.1:1
23.(2024·朝天)将一个高27cm的圆锥形容器装满水,倒入与它等底等高的圆柱形容器中,水的高度是( )cm。
A.81 B.27 C.13 D.9
24.(2024·朝天)把一个周长为12.56cm的圆分成两个半圆后,周长增加了( )cm。
A.0 B.4 C.8 D.12.56
25.(2024·朝天)如下图,以直角三角形ABC的直角边AB为轴旋转一周后得到的圆锥的底面直径是( )cm。
A.6 B.8 C.16 D.12
26.(2024·朝天)下列不具有相反意义的量的是( )
A.长大1岁和减少1kg。
B.盈利10元和亏损10元。
C.低于平均分10分和高于平均分15分。
D.向东走9m和向西走5m。
27.(2024·朝天)今年核桃平均每公顷的产量比去年增产二成,今年平均每公顷的产量相当于去年的( )%。
A.20 B.80 C.110 D.120
28.(2024·朝天)制作一个装广元贡茶的圆柱形封闭铁盒需要多少铁皮,实际上是计算它的( )
A.底面积 B.侧面积 C.表面积 D.体积
29.(2024·朝天)如果气温上升2℃表示为+2℃,那么气温下降5℃表示为( )℃。
A.﹣3 B.﹣5 C.+3 D.+7
30.(2024·江阳)六(1)班要买30个足球。甲、乙、丙三个体育用品商店采取不同的促销方式销售同种足球。六(1)班到( )购买合算些。
甲店(68元/个) 超过10个按八五折出售 乙店(68元/个) 买5个送1个 丙店(68元/个) 每满100元返现20元
A.甲店 B.乙店 C.丙店
31.(2024·江阳)把一根长3dm的木条依次锯了5次,得到同样长的小段,每段木条长是原木条的( )
A. B. C.
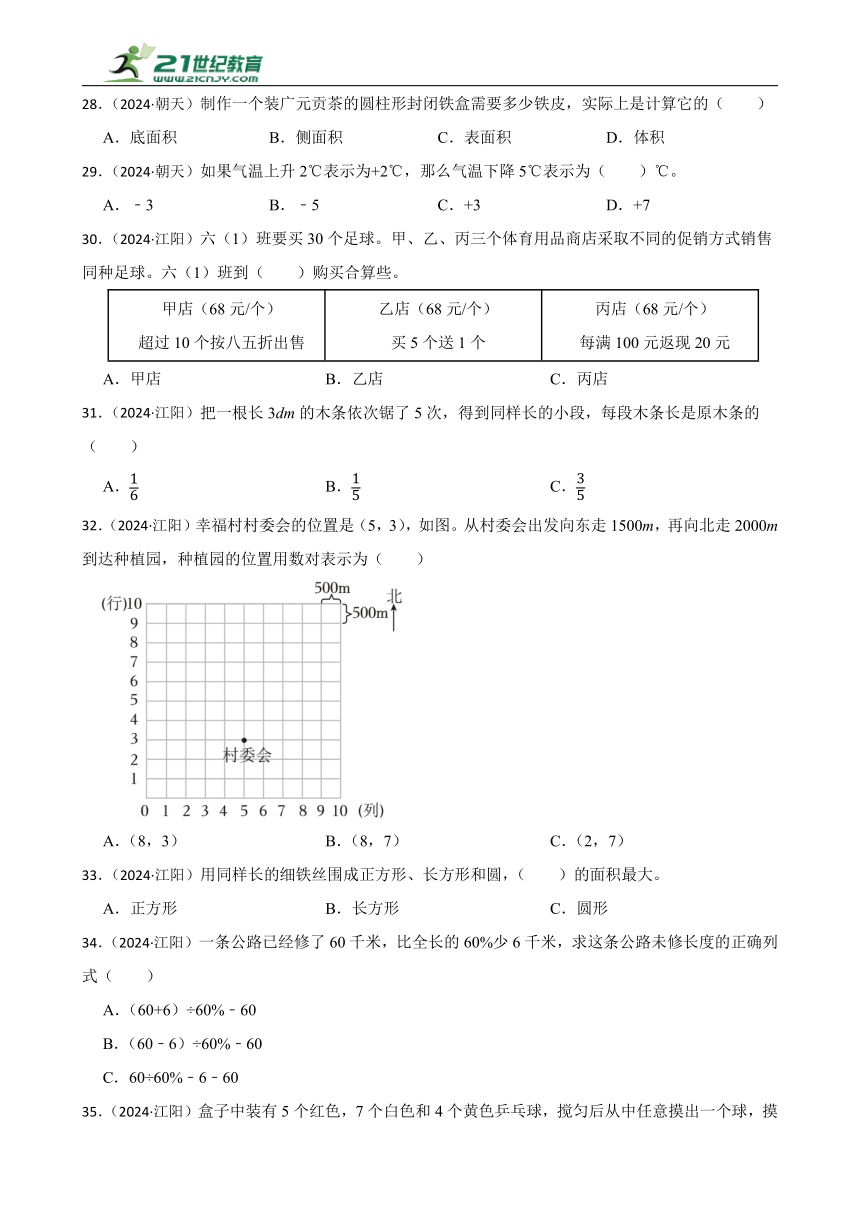
32.(2024·江阳)幸福村村委会的位置是(5,3),如图。从村委会出发向东走1500m,再向北走2000m到达种植园,种植园的位置用数对表示为( )
A.(8,3) B.(8,7) C.(2,7)
33.(2024·江阳)用同样长的细铁丝围成正方形、长方形和圆,( )的面积最大。
A.正方形 B.长方形 C.圆形
34.(2024·江阳)一条公路已经修了60千米,比全长的60%少6千米,求这条公路未修长度的正确列式( )
A.(60+6)÷60%﹣60
B.(60﹣6)÷60%﹣60
C.60÷60%﹣6﹣60
35.(2024·江阳)盒子中装有5个红色,7个白色和4个黄色乒乓球,搅匀后从中任意摸出一个球,摸到( )球的可能性最大。
A.红色 B.白色 C.黄色
36.(2024·金牛)如图,这一组图形的变化过程,可以用算式( )表示。
A. B. C. D.
37.(2024·金牛)妈妈骑共享单车去书店,买好书后,改为步行回家。下面图( )描述了妈妈去书店及返回的过程。
A. B.
C. D.
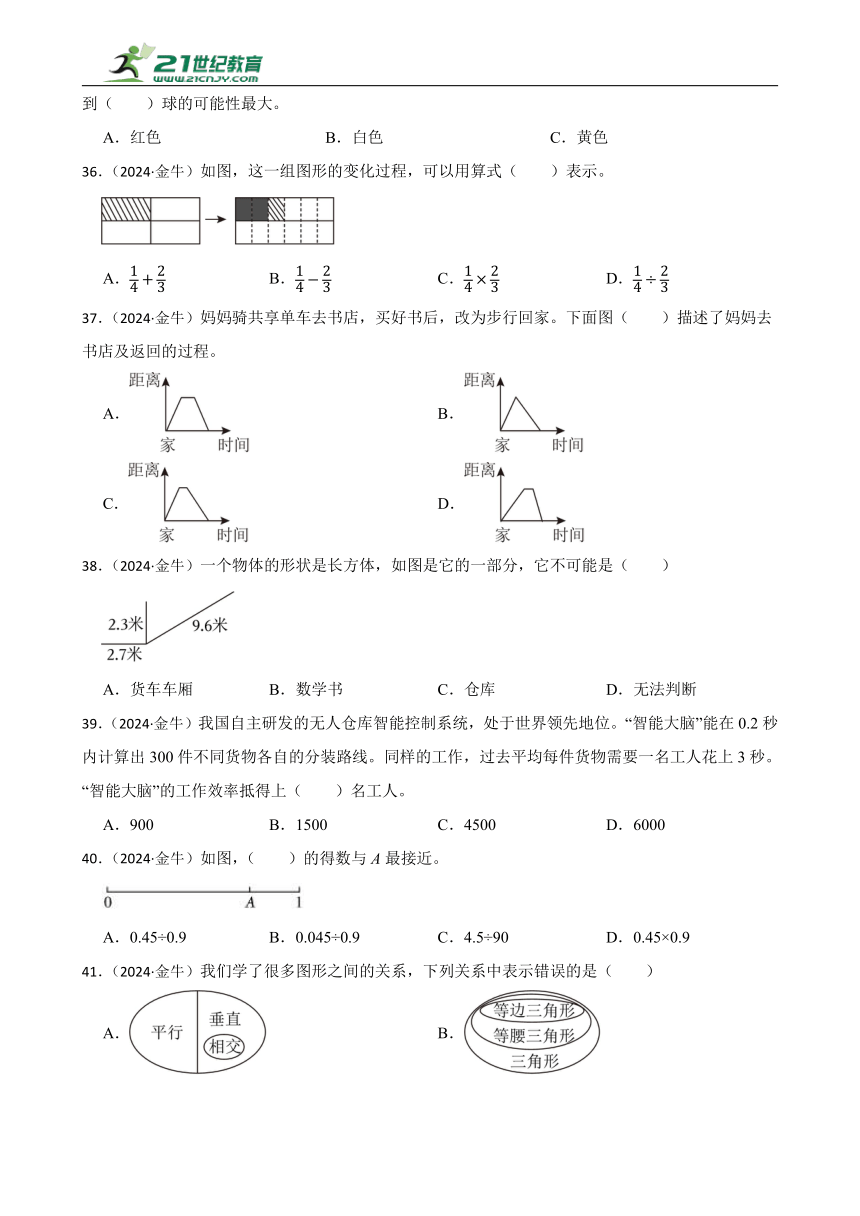
38.(2024·金牛)一个物体的形状是长方体,如图是它的一部分,它不可能是( )
A.货车车厢 B.数学书 C.仓库 D.无法判断
39.(2024·金牛)我国自主研发的无人仓库智能控制系统,处于世界领先地位。“智能大脑”能在0.2秒内计算出300件不同货物各自的分装路线。同样的工作,过去平均每件货物需要一名工人花上3秒。“智能大脑”的工作效率抵得上( )名工人。
A.900 B.1500 C.4500 D.6000
40.(2024·金牛)如图,( )的得数与A最接近。
A.0.45÷0.9 B.0.045÷0.9 C.4.5÷90 D.0.45×0.9
41.(2024·金牛)我们学了很多图形之间的关系,下列关系中表示错误的是( )
A. B.
C. D.
42.(2024·金牛)丽丽用8.4元买了3支中性笔,用竖式算出了每只中性笔的价格,如图,竖式中用方框圈出的这一步表示( )
A.24元 B.24角 C.24分 D.2角4分
43.(2024·达州)根据图中的规律,括号内应填的分数是( )
A. B. C. D.
44.(2024·达州)如图中的正方体、圆柱和圆锥底面积相等,高也相等。下面哪句话是正确的?( )
A.圆锥的体积是正方体的
B.圆柱的体积比正方体的体积小一些
C.圆柱体积与圆锥体积相等
D.正方体的体积比圆柱的小一些
45.(2024·达州)钢笔每支12元,圆珠笔每支7元,一共买了6支笔,用了52元,钢笔买了( )支。
A.1 B.2 C.3 D.4
46.(2023·新都)两个相同的三角形( )拼成一个平行四边形。
A.一定能 B.不太可能 C.不可能 D.有可能
47.(2023·新都)如图,把一个直径是2dm的圆平均分成若干份,剪开后拼成一个近似的平行四边形,这个平行四边形的周长是( )dm。
A.5.54 B.6.28 C.7.28 D.8.28
48.(2023·新都)下面能围成三角形的一组线段是( )
A.0.5厘米、1.8厘米、1厘米 B.1厘米、2.5厘米、3厘米
C.2厘米、2厘米、4厘米 D.10厘米、17厘米、2厘米
49.(2023·旌阳)按如图的方法堆放小球。第15堆有( ) 个小球。
A.95 B.105 C.110 D.120
50.(2023·旌阳)下面说法中,正确的一句是( )
A.想清楚地看出小明家2023年1月至6月天然气用量的增减变化情况,最好选用扇形统计图
B.一个圆锥的底面直径和高分别扩大到原来的2倍,它的体积就扩大到原来的4倍
C.东山小区植树101课,成活了100棵,成活率不满100%
D.平行四边形的面积与三角形的面积的比是2:1
答案解析部分
1.B
解:首先,计算第一件上衣的成本和利润:
第一件上衣的售价是120元,赚了20%,则其成本为
120÷(1+20%)=120÷1.2=10(元)
因此,第一件上衣赚了
120-100=20(元)
接着,计算第二件上衣的成本和亏损:
第二件上衣的售价同样是120元,亏了20%,则其成本为
120÷(1-20%)=120÷0.8=150(元)
因此,第二件上衣亏了
150-120=30(元)
最后,比较两件上衣的利润和亏损:
第一件上衣赚了20元,第二件上衣亏了30元,因此,总体上商店亏了。
30-20=10(元)。
故答案为:B。
本题和示例一的结构类似,都是关于两件商品,一件盈利、一件亏损,且盈利和亏损的百分比相同,售价也相同。我们需要通过计算每件商品的成本和盈亏,来确定商店整体是赚了、亏了,还是不赚不亏。
2.B
解:48×198≈50×200=10000(元)
故答案为:B。
根据“单价×数量=总价”,列出算式,把48看作50,198看作200进行估算即可。
3.C
解:A项:=(一定),a和b(a,b均不为0)成正比例关系;
B项:=(一定),a和b(a,b均不为0)成正比例关系;
C项:ab=(一定),a和b(a,b均不为0)成反比例关系;
D项:a和b(a,b均不为0)不成比例关系。
故答案为:C。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
4.A
解:设圆的半径为r厘米,则12.56r=3.14r2
12.56=3.14r
r=4;
圆的面积:3.14×42=50.24(平方厘米)
故答案为:A。
假设圆的半径为r,根据长方形和圆的面积相等,列出等式,化简算出圆的半径,再代入公式圆的面积=π计算即可。
5.A
解:1.2×=0.15,0.6×=0.15,所以可以组成比例1.2:0.6=:。
故答案为:A。
比例的基本性质:在比例里,两个内项积等于两个外项积。
6.A
解:比的前项和后项都扩大到原来的3倍,这个比值不变,还是 。
故答案为:A。
比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
7.A
解:A项:1~6这几个数中,奇数有3个,偶数有3个;这个游戏规则公平;
B项:1~6这几个数中,质数有3个,偶数有2个;这个游戏规则不公平;
C项:1~6这几个数中,小于3的数有2个,大于3的数有3个;这个游戏规则不公平;
D项:1~6这几个数中,小于4的数有3个,大于4的数有2个;这个游戏规则不公平。
故答案为:A。
分别写出1~6这几个数中奇数、偶数、质数、合数、以及小于3、小于4的数的个数,据此判断是否公平。
8.C
解:A项:在数轴上位于0的左侧2个单位距离;
B项:在数轴上位于0的右侧3个单位距离;
C项:在数轴上位于0的左侧1个单位距离;
D项:在数轴上位于0的右侧2.5个单位距离。
故答案为:C。
本题考查的是数轴上的点与数的对应关系,以及对数的大小和距离0远近的直观理解。数轴上,正数位于0的右侧,负数位于0的左侧,数轴上的点离0越近,该数与0的距离越小。
9.A
解:12÷3=4(厘米)。
故答案为:A。
等底等体积的圆柱和圆锥,圆锥的高是圆柱的3倍,据此计算即可。
10.A
解:看电影时的路程是不变的,排除D,因为星期天爸爸开车送小强去看电影,看完电影后,小强步行回家,则所用时间去时较少,返回时较多,A项符合情况。
故答案为:A。
依据题意,并且观察图像只有A项符合情况。
11.C
解:一个圆柱切拼成一个近似长方体后,体积不变,表面积增加了左、右两个面的面积。
故答案为:C。
物体所占空间的大小叫做它的体积,把圆柱切拼成一个近似长方体后,体积不变;
表面积增加了底面半径×高的两个面的面积。
12.C
解:2024÷4=506,2024年是闰年,2月29天;
31×3+29+30×2
=93+29+60
=122+60
=182(天)。
故答案为:C。
2024年是闰年,2月29天;今年上半年的总天数=这六个月的天数相加。
13.D
解:A项:因为1+>1,所以a×(1+)=a;
B项:因为1-<1,所以a×(1-)<a;
C项:因为1+>1,所以a÷(1+)<a;
D项: 因为1-<1,所以a÷(1-)=a;
a>a。
故答案为:D。
一个数(0和负数除外)除以小于1的数,所得的商大于原来的数;反之,商小于原来的数;一个数(0和负数除外)乘小于1的数,所得的积小于原来的数,反之,积大于原来的数。然后比较大小。
14.C
解:一座桥梁的限重较重,应该是30吨,即30T。
故答案为:C。
吨表示比较重的物体的质量,根据实际生活经验以及题干中的具体数据来进行选择。
15.B
解:圆锥的高是圆柱的高的3倍,圆柱的高与圆锥的高的比是1:3 。
故答案为:B。
底面积和体积都相等的圆柱和圆锥,圆锥的高是圆柱高的3倍。
16.B
解:(5×10):5=10:1。
故答案为:B。
先单位换算5厘米=50毫米,这幅图纸的比例尺=图上距离:实际距离。
17.D
解:百分数表示两个数之间的倍数关系,折扣、成数、税率可以用百分数表示,利息是一个具体的量,必须带单位,不能用百分数表示。
故答案为:D。
百分数是“表示一个数是另一个数的百分之几的数”,它只能表示两个数之间的倍数关系,不能表示某一具体的数量;所以百分数不能带单位名称。
18.C
解:n表示任意自然数,2n是偶数,则奇数是2n+1。
故答案为:C。
相邻的自然数相差1,n是自然数,2n是偶数,则奇数是2n+1。
19.B
A项:×=<1;
B项:×=<1;
C项:×=>1;
D项:×=>1;
<。
故答案为:B。
把各项的数分别代入计算,然后选择积小于1的最大的数是5。
20.C
解:37÷3=12(名)······1(名)
12+1=13(名)。
故答案为:C。
抽屉原理,至少在同一抽屉里相同物体的个数=物体总个数÷抽屉的个数+1。
21.B
解:180÷60%=300(元)。
故答案为:B。
这双童鞋的原价=现价÷折扣。
22.A
解:32:12=9:1。
故答案为:A。
当一个长方形按3:1的比例放大,这意味着其长和宽都变为原来的3倍。由于面积是长和宽的乘积,放大后的面积将会是原面积的3×3=9倍。因此,放大后的图形面积与原图形面积的比值是9:1。
23.D
解:27÷3=9(厘米)。
故答案为:D。
圆柱与圆锥等底等高,则圆柱形容器水面的高度=圆锥形容器水面的高度÷3。
24.C
解:12.56÷3.14×2
=4×2
=8(厘米)。
故答案为:C。
把圆分成两个半圆后,增加的周长=圆的直径×2;其中直径=周长÷π。
25.D
解:6×2=12(厘米)。
故答案为:D。
以直角三角形ABC的直角边AB为轴旋转一周后得到的圆锥的底面直径=直角三角形的底6厘米×2。
26.A
解:长大1岁和减少1kg单位不一致,不是具有相反意义的量。
故答案为:A。
盈利和亏损、低于平均分和高于平均分、向东走和向西走是具有相反意义的量。
27.D
解:1+20%=120%。
故答案为:D。
把去年的产量看作单位“1”,今年的产量=去年的产量+增加的成数。
28.C
解:需要铁皮的面积就是求它的表面积。
故答案为:C。
物体表面的面积是它的表面积。
29.B
解:气温下降5℃表示为-5℃。
故答案为:B。
正数和负数表示具有相反意义的量;气温上升记作正数,则气温下降记作负数。
30.C
解:甲店:68×30×85%
=2040×85%
=1734(元)
乙店:30÷(5+1)
=30÷6
=5(组)
(30﹣5)×68
=25×68
=1700(元)
丙店:68×30=2040(元)
2040÷100≈20(个)
2040﹣20×20%×100
=2040﹣400
=1640(元)
1640<1700<1734,所以在丙店购买合算些。
故答案为:C。
因为要买的足球个数大于10个,所以甲店是按八五折购买的;乙店是用花5个的钱可以买6个;丙店需要先按原价计算出30个足球的总价,再根据每满100元返现20元计算花的钱数;最后比较三家店所花钱数的大小,找出支付钱数最少的店即可。
31.A
解:1÷(5+1)=
故答案为:A。
把一根长3dm的木条依次锯了5次,就是把木条平均分成(5+1)段,利用分数的意义解答。
32.B
解:如图:
所以种植园的位置用数对表示为(8,7)
故答案为:B。
用数对表示位置时,先表示第几列,再表示第几行。幸福村村委会的位置是第5列第3行,从村委会出发向东走1500m,走了1500 ÷500=3(格),再向北走2000m,走了2000÷500=4(格)到达种植园,种植园的位置用数对表示第8列第7行。
33.C
解:假设铁丝的长是6.28米,设长方形的长是2米,宽是1.14米,
则面积:2×1.14=2.28(平方米);
正方形的面积为:(6.28÷4)×(6.28÷4)=2.4649(平方米)
圆的面积为:3.14×(6.28÷3.14÷2)2=3.14(平方米)
因为:3.14>2.4649>2.28,所以圆的面积最大。
故答案为:C。
根据正方形、长方形、圆的周长公式、面积公式,假设三根铁丝的长度是6.28米,分别求出它们的面积,然后进行比较。
34.A
解:(60+6)÷60%﹣60
=66÷60%﹣60
=110﹣60
=50(千米)
故答案为:A。
根据题意,60千米加6千米 是全长的60%,可以用除法求出全长,然后用全长减去已修长度就是未修长度。
35.B
解:7>5>4
故答案为:B。
数量越多,摸到的可能性越大,比较三种颜色球的数量,找到最多的,即可解答。
36.C
解:第一幅图中的阴影表示,第二幅图中的阴影表示的是多少,可以用算式表示。
故答案为:C。
本题考查分数乘法的意义与计算方法,第一幅图表示这个长方形的,第二幅图表示的是多少,根据分数乘法的意义,列式为,由此解答。
37.C
解:骑共享单车的速度要比步行的速度快,即从家去书店的时间要比从书店回家的时间更少,去到书店买书,停留一段时间,距离不变,只有C选项符合题意。
故答案为:C。
骑共享单车的速度要比步行的速度快,即从家去书店的时间要比从书店回家的时间更少,在书店买书需要时间停留,即在书店距离随着时间的变化而没有变化,根据生活实际,结合图像即可判断。
38.B
解:图片中该长方体的长、宽、高分别为2.7米、9.6米、2.3米,故不可能为数学书。
故答案为:B。
根据生活实际情况进行判断,数学书的长、宽、高不可能是图示数据。
39.C
解:3×300÷0.2=4500(名)。
故答案为:C。
同样的工作,说明工作总量一定,工作时间与工作效率成反比例关系,那么完成这300件货物每名工人的工作时间(3×300秒)是“智能大脑”时间(0.2秒)的几倍,那么“智能大脑”的工作效率就抵得上几名工人,用除法解决即可。
40.A
A:0.45÷0.9=0.5;
B:0.045÷0.9=0.05;
C:4.5÷90=0.05;
D:0.45×0.9=0.405;
由图可知,0.45÷0.9的得数与A选项结果最接近。
故答案为:A。
小数除法:先将被除数和除数同时扩大到相同的倍数,使除数变成整数,再按照除数是整数的方法计算;
小数乘小数:先按照整数乘法算出积,再点小数点,点小数点时,看因数中一共有几位小数,就从积的右边起数出几位,点上小数点;
由图可知,A的数值小于1,且大于0.5,根据运算法则计算出各项结果,再进行比较即可求解。
41.A
解:A选项中垂直是相交的一种特殊情况,该选项表示错误;
B选项中等边三角形和等腰三角形都是三角形,其中等边三角形是特殊的等腰三角形,该选项表示正确;
C选项中长方形与正方形都是平行四边形,正方形是特殊的长方形,该选项表示正确;
D选项中长方体、正方体、圆柱、圆锥都是立体图形,正方体是特殊的长方体,该选项表示正确。
故答案为:A。
同一平面内,平行和相交是两条直线的位置关系,其中垂直是相交的一种特殊情况;
三角形的分类按边分时,三角形包括不等边三角形和等腰三角形,其中等边三角形是特殊的等腰三角形;
平行四边形对边平行且相等,长方形与正方形都是平行四边形,正方形是特殊的长方形;
长方体、正方体、圆柱、圆锥都是立体图形,正方体是特殊的长方体。
42.B
解: 竖式中用方框圈出的这一步表示3乘8角等于24角。
故答案为:B。
由题意得,竖式中用方框圈出的这一步表示3支中性笔与8角的乘积。
43.D
解:分子从图一开始依次是3、5、7、9、11;分母依次是22、32、42、52、62。6层的分数是 。
故答案为:D。
依据规律分别找出分子、分母,6层这个分数是。
44.A
解:A项:圆锥的体积是正方体的,原题干说法正确;
B项:圆柱的体积与正方体的体积相等,原题干说法错误;
C项:圆柱体积是圆锥体积的3倍 ,原题干说法错误;
D项:正方体的体积与圆柱的体积相等 ,原题干说法错误。
故答案为:A。
正方体的体积=底面积×高;
圆柱的体积=底面积×高;
圆锥的体积=底面积×高×;则圆锥的体积是正方体的。
45.B
解:设钢笔买了x支,则圆珠笔有(6-x)支。
12x+7(6-x)=52
12x+42-7x=52
5x=10
x=10÷5
x=2。
故答案为:B。
设钢笔买了x支,则圆珠笔有(6-x)支。依据钢笔的单价×钢笔买的支数+圆珠笔的单价×圆珠笔买的支数=共花的钱数,列比例,解比例。
46.A
解:两个相同的三角形一定能拼成一个平行四边形。
故答案为:A。
任何一个平行四边形都可以沿对角线分割成两个一样的三角形,所以两个一样的三角形一定可以拼成平行四边形。
47.D
解:2×3.14+2=8.28(分米)。
故答案为:D。
把圆剪拼成平行四边形的过程中,平行四边形的周长=圆的周长+圆的直径;圆的周长=直径×π。
48.B
解:选项A:0.5厘米+1厘米=1.5厘米<1.8厘米,不能构成三角形;
选项B:任意两条边之和都大于第三条边,可以构成三角形;
选项C:2厘米+2厘米=4厘米,不能构成三角形;
选项D:10厘米+2厘米=12厘米<17厘米,不能构成三角形。
故答案为:B。
构成三角形的三条边,满足任意两条边的长度大于第三条边。
49.D
解:1+2+3+4+5+6+7+8+9+10+11+12+13+14+15
=(1+15)×7+8
=16×7+8
=112+8
=120(个);
故答案为:D。
第一堆有1个小球,第二堆有(1+2)个小球,第三堆有(1+2+3)个小球,第四堆有(1+2+3+4)个小球,可以发现,第n堆就有(1+2+3+…+n)个小球,据此解答。
50.C
解:选项A:想清楚地看出小明家2023年1月至6月天然气用量的增减变化情况,最好选用折线统计图,该说法错误;
选项B:圆锥的底面直径扩大到原来的2倍,即半径也扩大到原来的2倍,那么面积就扩大到原来的2×2=4倍,高也扩大到原来的2倍,体积就扩大到原来的4×2=8倍,该说法错误;
选项C:成活率是100÷101≈99.01%,成活率不满100%,该说法正确;
选项D:等底等高的平行四边形面积与三角形的面积比是2:1,该说法错误;
故答案为:C。
折线统计图不仅能表示数量的多少,还能表示出数量的增减变化情况;圆锥的底面直径扩大到原来的2倍,即半径也扩大到原来的2倍,那么面积就扩大到原来的(2×2)倍,圆锥体积=×底面积×高;成活率=成活数量÷总数量;等底等高的平行四边形面积是三角形面积的2倍。
小升初数学备考真题分类汇编(四川地区专版)
试卷说明:
本试卷试题精选自四川各市,县2024、2023近两年六年级下学期小升初期末真题试卷,难易度均衡,适合四川各市,县的六年级学生小升初择校考、分班考等复习备考使用!
一、单选题
1.(2024·北川)服装店售出的两件上衣都卖了120元。一件赚了20%,一件亏了20%。服装店在卖出这两件上衣时总体是( )
A.赚了 B.亏了 C.不赚不亏 D.无法确定
2.(2024·江阳)足球48元/个,杨老师要给学校足球队买198个足球,他大约要准备( )
A.8000元 B.10000元 C.100000元
3.(2024·朝天)下面式子中,a和b(a,b均不为0)成反比例关系的是( )
A.5a=4b B.= C.5a= D.5a=b+4
4.(2024·江阳)图中长方形和圆的面积相等,长方形的长是12.56cm,圆的面积是( )cm2。
A.50.24 B.25.12 C.12.56
5.(2024·达州)1.2:0.6可以和下面的( )组成一个比例。
A.: B.0.6:0.03 C.:0.8 D.12:0.06
6.(2024·朝天) 一个比的比值是,它的前项和后项都扩大到原来的3倍,这时比值是( )
A. B. C. D.
7.(2023·温江)淘气和笑笑玩掷骰子游戏,骰子各面上分别是1、2、3、4、5、6,下面( )
A.上面是奇数淘气胜,上面是偶数笑笑胜
B.上面是质数淘气胜,上面是合数笑笑胜
C.上面的数小于3淘气胜,上面的数大于3笑笑胜
D.上面的数小于4淘气胜,上面的数大于4笑笑胜
8.(2024·朝天)在带箭头的直线上表示下列各数,( )最接近0。
A.﹣2 B.3 C.﹣1 D.2.5
9.(2023·新都)一个圆柱与一个圆锥体积相等,底面积也相等。已知圆锥的高是12厘米,圆柱的高是( )厘米。
A.4 B.12 C.24 D.36
10.(2024·北川)星期天爸爸开车送小强去看电影,看完电影后,小强步行回家。下面能反映小强活动情况的是( )
A. B.
C. D.
11.(2024·北川)如下图,一个圆柱切拼成一个近似长方体后( )
A.表面积不变,体积不变。 B.表面积不变,体积变大。
C.表面积变大,体积不变。 D.表面积变大,体积变大。
12.(2024·北川)今年上半年的总天数是( )
A.180天 B.181天 C.182天 D.183天
13.(2024·北川)已知a>0,则下列各式中,得数最大的是( )
A.a×(1+) B.a×(1-) C.a÷(1+) D.a÷(1-)
14.(2024·北川)在一座桥梁旁,有一块限重的交通标志牌(如图),被污渍遮挡住的字母应当是( )
A.km B.Kg C.T D.L
15.(2023·叙永)一个圆柱与圆锥的体积相等,圆柱的半径与圆锥的半径相等,圆柱的高与圆锥的高的比是( )
A.3:1 B.1:3 C.9:1 D.1:9
16.(2024·北川) 一个圆柱形零件的高是5mm,画在图纸上的高是5cm。这幅图纸的比例尺是( )
A.1:1 B.10:1 C.1:10 D.10
17.(2024·北川)下面不能用百分数表示的是( )
A.折扣 B.成数 C.税率 D.利息
18.(2024·北川)用n表示自然数0、1、2、3、4、5、6……,表示奇数比较合适的是( )
A.n+1 B.n﹣1 C.2n+1 D.2n﹣1
19.(2024·朝天)式子×<1的□里可以填的最大整数是( )
A.4 B.5 C.6 D.7
20.(2024·朝天)手工课上老师给学生发折纸,有红、黄、蓝三种,每人发一种,如果这个班有37名学生,那么至少有( )名学生拿到相同颜色的折纸。
A.11 B.12 C.13 D.14
21.(2024·朝天)甜甜妈妈花了180元买了一双打六折的童鞋,这双童鞋的原价是( )元。
A.450 B.300 C.288 D.108
22.(2024·朝天) 一个长方形按3:1的比放大后,所得图形的面积与原图形的面积的比是( )
A.9:1 B.6:1 C.3:1 D.1:1
23.(2024·朝天)将一个高27cm的圆锥形容器装满水,倒入与它等底等高的圆柱形容器中,水的高度是( )cm。
A.81 B.27 C.13 D.9
24.(2024·朝天)把一个周长为12.56cm的圆分成两个半圆后,周长增加了( )cm。
A.0 B.4 C.8 D.12.56
25.(2024·朝天)如下图,以直角三角形ABC的直角边AB为轴旋转一周后得到的圆锥的底面直径是( )cm。
A.6 B.8 C.16 D.12
26.(2024·朝天)下列不具有相反意义的量的是( )
A.长大1岁和减少1kg。
B.盈利10元和亏损10元。
C.低于平均分10分和高于平均分15分。
D.向东走9m和向西走5m。
27.(2024·朝天)今年核桃平均每公顷的产量比去年增产二成,今年平均每公顷的产量相当于去年的( )%。
A.20 B.80 C.110 D.120
28.(2024·朝天)制作一个装广元贡茶的圆柱形封闭铁盒需要多少铁皮,实际上是计算它的( )
A.底面积 B.侧面积 C.表面积 D.体积
29.(2024·朝天)如果气温上升2℃表示为+2℃,那么气温下降5℃表示为( )℃。
A.﹣3 B.﹣5 C.+3 D.+7
30.(2024·江阳)六(1)班要买30个足球。甲、乙、丙三个体育用品商店采取不同的促销方式销售同种足球。六(1)班到( )购买合算些。
甲店(68元/个) 超过10个按八五折出售 乙店(68元/个) 买5个送1个 丙店(68元/个) 每满100元返现20元
A.甲店 B.乙店 C.丙店
31.(2024·江阳)把一根长3dm的木条依次锯了5次,得到同样长的小段,每段木条长是原木条的( )
A. B. C.
32.(2024·江阳)幸福村村委会的位置是(5,3),如图。从村委会出发向东走1500m,再向北走2000m到达种植园,种植园的位置用数对表示为( )
A.(8,3) B.(8,7) C.(2,7)
33.(2024·江阳)用同样长的细铁丝围成正方形、长方形和圆,( )的面积最大。
A.正方形 B.长方形 C.圆形
34.(2024·江阳)一条公路已经修了60千米,比全长的60%少6千米,求这条公路未修长度的正确列式( )
A.(60+6)÷60%﹣60
B.(60﹣6)÷60%﹣60
C.60÷60%﹣6﹣60
35.(2024·江阳)盒子中装有5个红色,7个白色和4个黄色乒乓球,搅匀后从中任意摸出一个球,摸到( )球的可能性最大。
A.红色 B.白色 C.黄色
36.(2024·金牛)如图,这一组图形的变化过程,可以用算式( )表示。
A. B. C. D.
37.(2024·金牛)妈妈骑共享单车去书店,买好书后,改为步行回家。下面图( )描述了妈妈去书店及返回的过程。
A. B.
C. D.
38.(2024·金牛)一个物体的形状是长方体,如图是它的一部分,它不可能是( )
A.货车车厢 B.数学书 C.仓库 D.无法判断
39.(2024·金牛)我国自主研发的无人仓库智能控制系统,处于世界领先地位。“智能大脑”能在0.2秒内计算出300件不同货物各自的分装路线。同样的工作,过去平均每件货物需要一名工人花上3秒。“智能大脑”的工作效率抵得上( )名工人。
A.900 B.1500 C.4500 D.6000
40.(2024·金牛)如图,( )的得数与A最接近。
A.0.45÷0.9 B.0.045÷0.9 C.4.5÷90 D.0.45×0.9
41.(2024·金牛)我们学了很多图形之间的关系,下列关系中表示错误的是( )
A. B.
C. D.
42.(2024·金牛)丽丽用8.4元买了3支中性笔,用竖式算出了每只中性笔的价格,如图,竖式中用方框圈出的这一步表示( )
A.24元 B.24角 C.24分 D.2角4分
43.(2024·达州)根据图中的规律,括号内应填的分数是( )
A. B. C. D.
44.(2024·达州)如图中的正方体、圆柱和圆锥底面积相等,高也相等。下面哪句话是正确的?( )
A.圆锥的体积是正方体的
B.圆柱的体积比正方体的体积小一些
C.圆柱体积与圆锥体积相等
D.正方体的体积比圆柱的小一些
45.(2024·达州)钢笔每支12元,圆珠笔每支7元,一共买了6支笔,用了52元,钢笔买了( )支。
A.1 B.2 C.3 D.4
46.(2023·新都)两个相同的三角形( )拼成一个平行四边形。
A.一定能 B.不太可能 C.不可能 D.有可能
47.(2023·新都)如图,把一个直径是2dm的圆平均分成若干份,剪开后拼成一个近似的平行四边形,这个平行四边形的周长是( )dm。
A.5.54 B.6.28 C.7.28 D.8.28
48.(2023·新都)下面能围成三角形的一组线段是( )
A.0.5厘米、1.8厘米、1厘米 B.1厘米、2.5厘米、3厘米
C.2厘米、2厘米、4厘米 D.10厘米、17厘米、2厘米
49.(2023·旌阳)按如图的方法堆放小球。第15堆有( ) 个小球。
A.95 B.105 C.110 D.120
50.(2023·旌阳)下面说法中,正确的一句是( )
A.想清楚地看出小明家2023年1月至6月天然气用量的增减变化情况,最好选用扇形统计图
B.一个圆锥的底面直径和高分别扩大到原来的2倍,它的体积就扩大到原来的4倍
C.东山小区植树101课,成活了100棵,成活率不满100%
D.平行四边形的面积与三角形的面积的比是2:1
答案解析部分
1.B
解:首先,计算第一件上衣的成本和利润:
第一件上衣的售价是120元,赚了20%,则其成本为
120÷(1+20%)=120÷1.2=10(元)
因此,第一件上衣赚了
120-100=20(元)
接着,计算第二件上衣的成本和亏损:
第二件上衣的售价同样是120元,亏了20%,则其成本为
120÷(1-20%)=120÷0.8=150(元)
因此,第二件上衣亏了
150-120=30(元)
最后,比较两件上衣的利润和亏损:
第一件上衣赚了20元,第二件上衣亏了30元,因此,总体上商店亏了。
30-20=10(元)。
故答案为:B。
本题和示例一的结构类似,都是关于两件商品,一件盈利、一件亏损,且盈利和亏损的百分比相同,售价也相同。我们需要通过计算每件商品的成本和盈亏,来确定商店整体是赚了、亏了,还是不赚不亏。
2.B
解:48×198≈50×200=10000(元)
故答案为:B。
根据“单价×数量=总价”,列出算式,把48看作50,198看作200进行估算即可。
3.C
解:A项:=(一定),a和b(a,b均不为0)成正比例关系;
B项:=(一定),a和b(a,b均不为0)成正比例关系;
C项:ab=(一定),a和b(a,b均不为0)成反比例关系;
D项:a和b(a,b均不为0)不成比例关系。
故答案为:C。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
4.A
解:设圆的半径为r厘米,则12.56r=3.14r2
12.56=3.14r
r=4;
圆的面积:3.14×42=50.24(平方厘米)
故答案为:A。
假设圆的半径为r,根据长方形和圆的面积相等,列出等式,化简算出圆的半径,再代入公式圆的面积=π计算即可。
5.A
解:1.2×=0.15,0.6×=0.15,所以可以组成比例1.2:0.6=:。
故答案为:A。
比例的基本性质:在比例里,两个内项积等于两个外项积。
6.A
解:比的前项和后项都扩大到原来的3倍,这个比值不变,还是 。
故答案为:A。
比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
7.A
解:A项:1~6这几个数中,奇数有3个,偶数有3个;这个游戏规则公平;
B项:1~6这几个数中,质数有3个,偶数有2个;这个游戏规则不公平;
C项:1~6这几个数中,小于3的数有2个,大于3的数有3个;这个游戏规则不公平;
D项:1~6这几个数中,小于4的数有3个,大于4的数有2个;这个游戏规则不公平。
故答案为:A。
分别写出1~6这几个数中奇数、偶数、质数、合数、以及小于3、小于4的数的个数,据此判断是否公平。
8.C
解:A项:在数轴上位于0的左侧2个单位距离;
B项:在数轴上位于0的右侧3个单位距离;
C项:在数轴上位于0的左侧1个单位距离;
D项:在数轴上位于0的右侧2.5个单位距离。
故答案为:C。
本题考查的是数轴上的点与数的对应关系,以及对数的大小和距离0远近的直观理解。数轴上,正数位于0的右侧,负数位于0的左侧,数轴上的点离0越近,该数与0的距离越小。
9.A
解:12÷3=4(厘米)。
故答案为:A。
等底等体积的圆柱和圆锥,圆锥的高是圆柱的3倍,据此计算即可。
10.A
解:看电影时的路程是不变的,排除D,因为星期天爸爸开车送小强去看电影,看完电影后,小强步行回家,则所用时间去时较少,返回时较多,A项符合情况。
故答案为:A。
依据题意,并且观察图像只有A项符合情况。
11.C
解:一个圆柱切拼成一个近似长方体后,体积不变,表面积增加了左、右两个面的面积。
故答案为:C。
物体所占空间的大小叫做它的体积,把圆柱切拼成一个近似长方体后,体积不变;
表面积增加了底面半径×高的两个面的面积。
12.C
解:2024÷4=506,2024年是闰年,2月29天;
31×3+29+30×2
=93+29+60
=122+60
=182(天)。
故答案为:C。
2024年是闰年,2月29天;今年上半年的总天数=这六个月的天数相加。
13.D
解:A项:因为1+>1,所以a×(1+)=a;
B项:因为1-<1,所以a×(1-)<a;
C项:因为1+>1,所以a÷(1+)<a;
D项: 因为1-<1,所以a÷(1-)=a;
a>a。
故答案为:D。
一个数(0和负数除外)除以小于1的数,所得的商大于原来的数;反之,商小于原来的数;一个数(0和负数除外)乘小于1的数,所得的积小于原来的数,反之,积大于原来的数。然后比较大小。
14.C
解:一座桥梁的限重较重,应该是30吨,即30T。
故答案为:C。
吨表示比较重的物体的质量,根据实际生活经验以及题干中的具体数据来进行选择。
15.B
解:圆锥的高是圆柱的高的3倍,圆柱的高与圆锥的高的比是1:3 。
故答案为:B。
底面积和体积都相等的圆柱和圆锥,圆锥的高是圆柱高的3倍。
16.B
解:(5×10):5=10:1。
故答案为:B。
先单位换算5厘米=50毫米,这幅图纸的比例尺=图上距离:实际距离。
17.D
解:百分数表示两个数之间的倍数关系,折扣、成数、税率可以用百分数表示,利息是一个具体的量,必须带单位,不能用百分数表示。
故答案为:D。
百分数是“表示一个数是另一个数的百分之几的数”,它只能表示两个数之间的倍数关系,不能表示某一具体的数量;所以百分数不能带单位名称。
18.C
解:n表示任意自然数,2n是偶数,则奇数是2n+1。
故答案为:C。
相邻的自然数相差1,n是自然数,2n是偶数,则奇数是2n+1。
19.B
A项:×=<1;
B项:×=<1;
C项:×=>1;
D项:×=>1;
<。
故答案为:B。
把各项的数分别代入计算,然后选择积小于1的最大的数是5。
20.C
解:37÷3=12(名)······1(名)
12+1=13(名)。
故答案为:C。
抽屉原理,至少在同一抽屉里相同物体的个数=物体总个数÷抽屉的个数+1。
21.B
解:180÷60%=300(元)。
故答案为:B。
这双童鞋的原价=现价÷折扣。
22.A
解:32:12=9:1。
故答案为:A。
当一个长方形按3:1的比例放大,这意味着其长和宽都变为原来的3倍。由于面积是长和宽的乘积,放大后的面积将会是原面积的3×3=9倍。因此,放大后的图形面积与原图形面积的比值是9:1。
23.D
解:27÷3=9(厘米)。
故答案为:D。
圆柱与圆锥等底等高,则圆柱形容器水面的高度=圆锥形容器水面的高度÷3。
24.C
解:12.56÷3.14×2
=4×2
=8(厘米)。
故答案为:C。
把圆分成两个半圆后,增加的周长=圆的直径×2;其中直径=周长÷π。
25.D
解:6×2=12(厘米)。
故答案为:D。
以直角三角形ABC的直角边AB为轴旋转一周后得到的圆锥的底面直径=直角三角形的底6厘米×2。
26.A
解:长大1岁和减少1kg单位不一致,不是具有相反意义的量。
故答案为:A。
盈利和亏损、低于平均分和高于平均分、向东走和向西走是具有相反意义的量。
27.D
解:1+20%=120%。
故答案为:D。
把去年的产量看作单位“1”,今年的产量=去年的产量+增加的成数。
28.C
解:需要铁皮的面积就是求它的表面积。
故答案为:C。
物体表面的面积是它的表面积。
29.B
解:气温下降5℃表示为-5℃。
故答案为:B。
正数和负数表示具有相反意义的量;气温上升记作正数,则气温下降记作负数。
30.C
解:甲店:68×30×85%
=2040×85%
=1734(元)
乙店:30÷(5+1)
=30÷6
=5(组)
(30﹣5)×68
=25×68
=1700(元)
丙店:68×30=2040(元)
2040÷100≈20(个)
2040﹣20×20%×100
=2040﹣400
=1640(元)
1640<1700<1734,所以在丙店购买合算些。
故答案为:C。
因为要买的足球个数大于10个,所以甲店是按八五折购买的;乙店是用花5个的钱可以买6个;丙店需要先按原价计算出30个足球的总价,再根据每满100元返现20元计算花的钱数;最后比较三家店所花钱数的大小,找出支付钱数最少的店即可。
31.A
解:1÷(5+1)=
故答案为:A。
把一根长3dm的木条依次锯了5次,就是把木条平均分成(5+1)段,利用分数的意义解答。
32.B
解:如图:
所以种植园的位置用数对表示为(8,7)
故答案为:B。
用数对表示位置时,先表示第几列,再表示第几行。幸福村村委会的位置是第5列第3行,从村委会出发向东走1500m,走了1500 ÷500=3(格),再向北走2000m,走了2000÷500=4(格)到达种植园,种植园的位置用数对表示第8列第7行。
33.C
解:假设铁丝的长是6.28米,设长方形的长是2米,宽是1.14米,
则面积:2×1.14=2.28(平方米);
正方形的面积为:(6.28÷4)×(6.28÷4)=2.4649(平方米)
圆的面积为:3.14×(6.28÷3.14÷2)2=3.14(平方米)
因为:3.14>2.4649>2.28,所以圆的面积最大。
故答案为:C。
根据正方形、长方形、圆的周长公式、面积公式,假设三根铁丝的长度是6.28米,分别求出它们的面积,然后进行比较。
34.A
解:(60+6)÷60%﹣60
=66÷60%﹣60
=110﹣60
=50(千米)
故答案为:A。
根据题意,60千米加6千米 是全长的60%,可以用除法求出全长,然后用全长减去已修长度就是未修长度。
35.B
解:7>5>4
故答案为:B。
数量越多,摸到的可能性越大,比较三种颜色球的数量,找到最多的,即可解答。
36.C
解:第一幅图中的阴影表示,第二幅图中的阴影表示的是多少,可以用算式表示。
故答案为:C。
本题考查分数乘法的意义与计算方法,第一幅图表示这个长方形的,第二幅图表示的是多少,根据分数乘法的意义,列式为,由此解答。
37.C
解:骑共享单车的速度要比步行的速度快,即从家去书店的时间要比从书店回家的时间更少,去到书店买书,停留一段时间,距离不变,只有C选项符合题意。
故答案为:C。
骑共享单车的速度要比步行的速度快,即从家去书店的时间要比从书店回家的时间更少,在书店买书需要时间停留,即在书店距离随着时间的变化而没有变化,根据生活实际,结合图像即可判断。
38.B
解:图片中该长方体的长、宽、高分别为2.7米、9.6米、2.3米,故不可能为数学书。
故答案为:B。
根据生活实际情况进行判断,数学书的长、宽、高不可能是图示数据。
39.C
解:3×300÷0.2=4500(名)。
故答案为:C。
同样的工作,说明工作总量一定,工作时间与工作效率成反比例关系,那么完成这300件货物每名工人的工作时间(3×300秒)是“智能大脑”时间(0.2秒)的几倍,那么“智能大脑”的工作效率就抵得上几名工人,用除法解决即可。
40.A
A:0.45÷0.9=0.5;
B:0.045÷0.9=0.05;
C:4.5÷90=0.05;
D:0.45×0.9=0.405;
由图可知,0.45÷0.9的得数与A选项结果最接近。
故答案为:A。
小数除法:先将被除数和除数同时扩大到相同的倍数,使除数变成整数,再按照除数是整数的方法计算;
小数乘小数:先按照整数乘法算出积,再点小数点,点小数点时,看因数中一共有几位小数,就从积的右边起数出几位,点上小数点;
由图可知,A的数值小于1,且大于0.5,根据运算法则计算出各项结果,再进行比较即可求解。
41.A
解:A选项中垂直是相交的一种特殊情况,该选项表示错误;
B选项中等边三角形和等腰三角形都是三角形,其中等边三角形是特殊的等腰三角形,该选项表示正确;
C选项中长方形与正方形都是平行四边形,正方形是特殊的长方形,该选项表示正确;
D选项中长方体、正方体、圆柱、圆锥都是立体图形,正方体是特殊的长方体,该选项表示正确。
故答案为:A。
同一平面内,平行和相交是两条直线的位置关系,其中垂直是相交的一种特殊情况;
三角形的分类按边分时,三角形包括不等边三角形和等腰三角形,其中等边三角形是特殊的等腰三角形;
平行四边形对边平行且相等,长方形与正方形都是平行四边形,正方形是特殊的长方形;
长方体、正方体、圆柱、圆锥都是立体图形,正方体是特殊的长方体。
42.B
解: 竖式中用方框圈出的这一步表示3乘8角等于24角。
故答案为:B。
由题意得,竖式中用方框圈出的这一步表示3支中性笔与8角的乘积。
43.D
解:分子从图一开始依次是3、5、7、9、11;分母依次是22、32、42、52、62。6层的分数是 。
故答案为:D。
依据规律分别找出分子、分母,6层这个分数是。
44.A
解:A项:圆锥的体积是正方体的,原题干说法正确;
B项:圆柱的体积与正方体的体积相等,原题干说法错误;
C项:圆柱体积是圆锥体积的3倍 ,原题干说法错误;
D项:正方体的体积与圆柱的体积相等 ,原题干说法错误。
故答案为:A。
正方体的体积=底面积×高;
圆柱的体积=底面积×高;
圆锥的体积=底面积×高×;则圆锥的体积是正方体的。
45.B
解:设钢笔买了x支,则圆珠笔有(6-x)支。
12x+7(6-x)=52
12x+42-7x=52
5x=10
x=10÷5
x=2。
故答案为:B。
设钢笔买了x支,则圆珠笔有(6-x)支。依据钢笔的单价×钢笔买的支数+圆珠笔的单价×圆珠笔买的支数=共花的钱数,列比例,解比例。
46.A
解:两个相同的三角形一定能拼成一个平行四边形。
故答案为:A。
任何一个平行四边形都可以沿对角线分割成两个一样的三角形,所以两个一样的三角形一定可以拼成平行四边形。
47.D
解:2×3.14+2=8.28(分米)。
故答案为:D。
把圆剪拼成平行四边形的过程中,平行四边形的周长=圆的周长+圆的直径;圆的周长=直径×π。
48.B
解:选项A:0.5厘米+1厘米=1.5厘米<1.8厘米,不能构成三角形;
选项B:任意两条边之和都大于第三条边,可以构成三角形;
选项C:2厘米+2厘米=4厘米,不能构成三角形;
选项D:10厘米+2厘米=12厘米<17厘米,不能构成三角形。
故答案为:B。
构成三角形的三条边,满足任意两条边的长度大于第三条边。
49.D
解:1+2+3+4+5+6+7+8+9+10+11+12+13+14+15
=(1+15)×7+8
=16×7+8
=112+8
=120(个);
故答案为:D。
第一堆有1个小球,第二堆有(1+2)个小球,第三堆有(1+2+3)个小球,第四堆有(1+2+3+4)个小球,可以发现,第n堆就有(1+2+3+…+n)个小球,据此解答。
50.C
解:选项A:想清楚地看出小明家2023年1月至6月天然气用量的增减变化情况,最好选用折线统计图,该说法错误;
选项B:圆锥的底面直径扩大到原来的2倍,即半径也扩大到原来的2倍,那么面积就扩大到原来的2×2=4倍,高也扩大到原来的2倍,体积就扩大到原来的4×2=8倍,该说法错误;
选项C:成活率是100÷101≈99.01%,成活率不满100%,该说法正确;
选项D:等底等高的平行四边形面积与三角形的面积比是2:1,该说法错误;
故答案为:C。
折线统计图不仅能表示数量的多少,还能表示出数量的增减变化情况;圆锥的底面直径扩大到原来的2倍,即半径也扩大到原来的2倍,那么面积就扩大到原来的(2×2)倍,圆锥体积=×底面积×高;成活率=成活数量÷总数量;等底等高的平行四边形面积是三角形面积的2倍。
同课章节目录
