2024-2025学年小升初数学备考真题分类汇编(四川地区专版)专题2 单项选择题(含解析)
文档属性
| 名称 | 2024-2025学年小升初数学备考真题分类汇编(四川地区专版)专题2 单项选择题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 219.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 07:38:41 | ||
图片预览




文档简介
专题2 选择题-2023-2024学年
小升初数学备考真题分类汇编(四川地区专版)
试卷说明:
本试卷试题精选自四川各市,县2024、2023近两年六年级下学期小升初期末真题试卷,难易度均衡,适合四川各市,县的六年级学生小升初择校考、分班考等复习备考使用!
一、单选题
1.(2024·乐山)—个直角三角形的三条边长分别为3cm、4cm和5cm,这个三角形斜边上的高是( )
A.3cm B.6cm C.5cm D.2.4cm
2.(2024·乐山)将一个底边是8厘米的平行四边形沿高剪开,再拼成一个长方形,量得长方形的周长是28厘米,那么平行四边形的面积应该是( )平方厘米。
A.80 B.64 C.48 D.40
3.(2024·乐山)三个连续的非零自然数的积一定( )
A.既是奇数又是合数。 B.既是偶数又是质数。
C.既是奇数又是质数。 D.既是偶数又是合数。
4.(2024·乐山)峨眉山万年寺二月份某天的气温波动范围是﹣2℃~7℃,万年寺这天的最高气温与最低气温相差( )
A.5℃ B.﹣5℃ C.9℃ D.﹣9℃
5.(2024·乐山)2024年是新中国成立75周年,这一年的第一季度有( )天。
A.90 B.91 C.89 D.92
6.(2024·乐山)一个三位数,同时是2、3、5的倍数,这个数最大是( )
A.999 B.995 C.998 D.990
7.(2023·温江)把一个底面半径是5厘米的圆锥,完全浸没在一个底面直径是20厘米的圆柱形水槽中(如下图),取出圆锥后,水面下降了3厘米,这个圆锥高( )cm。
A.6 B.12 C.36 D.48
8.(2024·乐山)如果★代表一个非零自然数,那么下列式子中,结果最大的是( )
A.★× B.★÷ C.÷★ D.★×1
9.(2023·旌阳)把一克药粉放入100克水中,药粉与药水的质量比是( )
A.1:100 B.1:99 C.1:101 D.100:101
10.(2024·成都)在“观察物体”的课堂上,数学老师要求同学们搭出从以下两个方向看到的立体图形,那么同学们最少需要____个正方体,最多可以用____个正方体。 ( )
A.4和7 B.5和7 C.4和6 D.5和6
11.(2024·成都)一个微型零件长4mm,按80:1的比画在图纸上,在图纸上的长度是 ( )cm.
A.0.32 B.3.2 C.32 D.320
12.(2024·成都)认真观察下面这组图,第一幅图的点数为1,第2幅图的点数为5……
按照上面的规律,第n幅图的点数为 ( )
A.4n﹣3 B.4n+3 C.6n﹣2 D.6n+4
13.(2023·旌阳)已知,那么a、b、c的大小关系是( )
A.a>b>c B.b>a>c C.c>b>a D.b>c>a
14.(2024·成都)如图所示能用“表示或解决”的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
15.(2024·成都)下面的成语中,按照事件发生的可能性大小,从高到低排列正确的是 ( )
①十拿九稳 ②凤毛麟角 ③海枯石烂 ④万无一失
A.①②③④ B.④①②③ C.③④①② D.②③④①
16.(2023·新都)两个完全一样的正方体拼成一个长方体后,表面积的总和( )
A.增加了 B.减少了 C.不变 D.消失了
17.(2023·新都)一个圆的面积与它的直径( )
A.成正比例 B.成反比例 C.不成比例 D.无关联
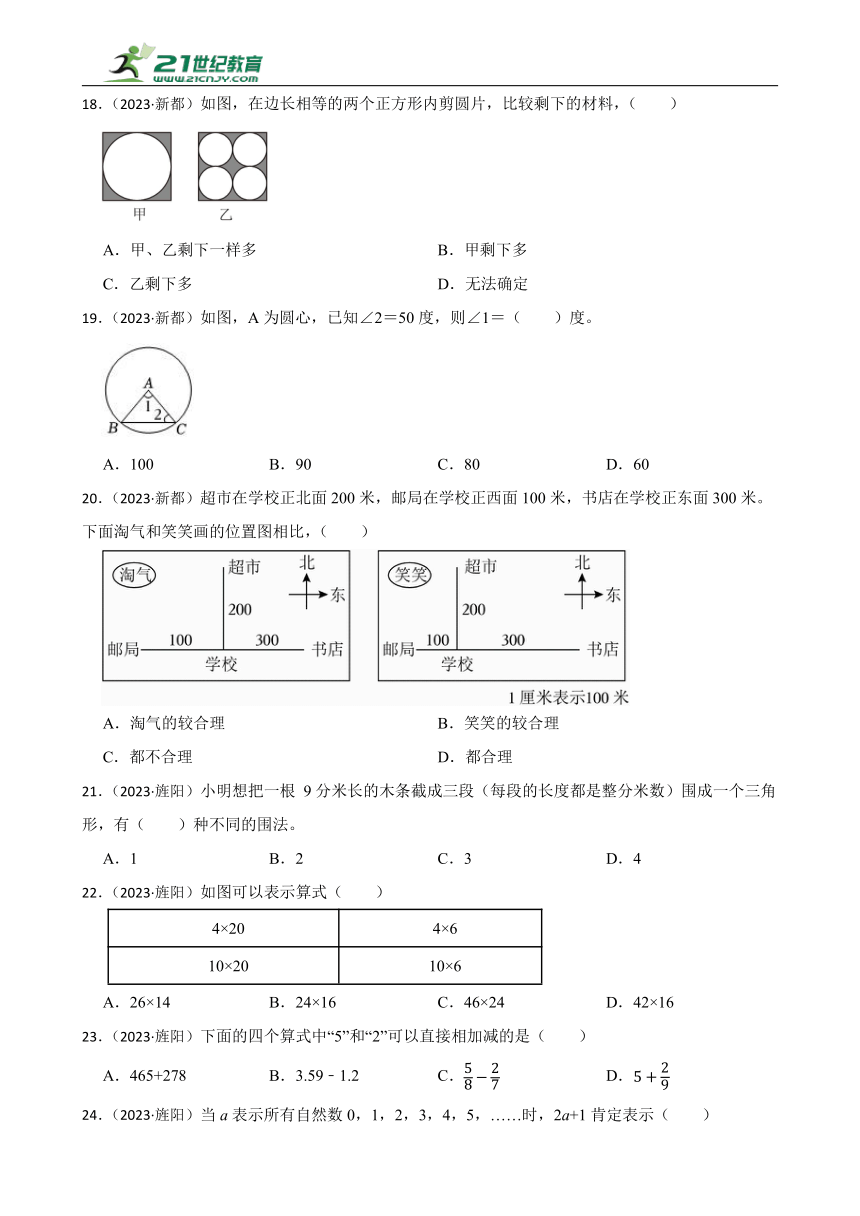
18.(2023·新都)如图,在边长相等的两个正方形内剪圆片,比较剩下的材料,( )
A.甲、乙剩下一样多 B.甲剩下多
C.乙剩下多 D.无法确定
19.(2023·新都)如图,A为圆心,已知∠2=50度,则∠1=( )度。
A.100 B.90 C.80 D.60
20.(2023·新都)超市在学校正北面200米,邮局在学校正西面100米,书店在学校正东面300米。下面淘气和笑笑画的位置图相比,( )
A.淘气的较合理 B.笑笑的较合理
C.都不合理 D.都合理
21.(2023·旌阳)小明想把一根 9分米长的木条截成三段(每段的长度都是整分米数)围成一个三角形,有( )种不同的围法。
A.1 B.2 C.3 D.4
22.(2023·旌阳)如图可以表示算式( )
4×20 4×6
10×20 10×6
A.26×14 B.24×16 C.46×24 D.42×16
23.(2023·旌阳)下面的四个算式中“5”和“2”可以直接相加减的是( )
A.465+278 B.3.59﹣1.2 C. D.
24.(2023·旌阳)当a表示所有自然数0,1,2,3,4,5,……时,2a+1肯定表示( )
A.奇数 B.偶数 C.质数 D.合数
25.(2023·旌阳)下面四组相关联的量中,成正比例的是( )
A.看一本书,每天看的页数和看的天数
B.圆锥的体积一定。它的底面积和高
C.修一条路,已经修的米数和剩下的米数
D.同一时间、地点,每棵树的高度和它影子的长度
26.(2023·温江)一个长方体长、宽、高分别是5米、4米、3米,把它的长减少1米后,新的长方体体积比原来减少( )立方米
A.12 B.15 C.20 D.48
27.(2023·温江)在一幅比例尺是1:5000000的地图上,量得成都到北京的距离约是30厘米,成都到北京的实际距离约是( )千米。
A.15 B.150 C.1500 D.15000
28.(2023·温江)在2000年前我国古代名著《周髀算经》中,关于圆的周长与直径的关系有这样的记载:“周三径一”。下面呈现了“周三径一”的是( )
A. B.
C. D.
29.(2023·温江)下面各项中,两个量成正比例的是( )
A.路程一定,行驶的速度与时间
B.一个数与它的倒数
C.两个数的和一定,一个加数与另一个加数
D.三角形的底一定,它的面积和高
30.(2023·阆中)仓库的角落里有一堆存放货物的正方体纸箱,从三个不同方位看到的形状图如图,这堆货物可能有( )箱。
A.8 B.10 C.11 D.15
31.(2023·阆中)在学校一条长50米的跑道两旁,从头到尾每隔5米插一面彩旗,一共要插( )面彩旗。
A.22 B.20 C.11 D.10
32.(2023·温江)如图,如果m点表示的数是,则n点表示的数是( )
A.﹣2 B.﹣0.25 C.﹣0.125 D.
33.(2023·温江)如果A=2×3×5,B=2×5×7,那么A和B的最大公因数和最小公倍数分别是( )
A.10和210 B.15和30 C.25和100 D.35和70
34.(2023·温江)一个两位数,个位上是最小的质数,十位上是最小的合数( )
A.42 B.12 C.21 D.24
35.(2023·阆中) + 的和里有( )个 。
A.1 B.3 C.9 D.15
36.(2023·叙永)如图表示的算式是( )
A. ×10 B. ×8 C. × D. ×
37.(2023·叙永)已知a×50%=b×=c÷0.25(a,b,c均不为0),则a,b,c的大小关系是( )
A.a>b>c B.b>c>a C.c>a>b D.a<b<c
38.(2023·阆中)一个直角三角形的两条直角边AB=6 厘米和AC=8 厘米,斜边BC上的高是4.8厘米,那么三角形ABC的周长是( )厘米。
A.18.8 B.24 C.28.8 D.48
39.(2023·阆中)如图这样用小棒搭了3间房子,那么搭100间需要用( )根小棒。
A.400 B.401 C.500 D.501
40.(2023·阆中)在算式x÷y=10……7,把x,y同时扩大到原来的10倍后,商和余数分别是( )
A.10和7 B.10和70 C.100和7 D.100和70
41.(2023·阆中)小军班同学的平均身高是142厘米,小红班同学的平均身高是146厘米,若比较小军和小红两人的身高,则( )
A.小军高 B.小红高 C.一样高 D.不能确定
42.(2023·成都模拟)四个同样大小的圆柱拼成一个高为40cm的大圆柱时 ,表面积减少了72cm2 ,原来每个小圆柱的体积是( ) cm3。
A.120 B.360 C.480 D.720
43.(2023·阆中)商店搞促销活动,所有春装打七折出售,现价是原价的( )
A.3% B.7% C.30% D.70%
44.(2023·阆中)把小丽以大树为起点向东走10m记作+10m,小丽以大树为起点向西走8m记作( )
A.﹣10m B.+10m C.﹣8m D.+8m
45.(2023·旌阳)图书馆到学校的实际距离是15km,在一幅地图上量得这两地的距离是3cm,这幅图的比例尺是( )
A.1:5 B.1:5000 C.1:50000 D.1:500000
46.(2023·成都模拟)“五一”大假,甲、乙两个店各推出促销措施,甲店九折优惠,乙店购买100元货物赠送价值10元的购物券一张,妈妈准备花掉500元钱,去( ) 店更优惠。
A.甲 B.乙 C.甲、乙任选 D.无法比较
47.(2023·成都模拟)一件工作原计划6天完成,实际5天就完工,工作效率提高了( )。
A. B. C. D.
答案解析部分
1.D
解:3×4÷2×2÷5=2.4(cm)
故答案为:D。
三角形面积=底×高÷2,直角三角形两条直角边分别为三角形的底和高,根据两条直角边的长度求出三角形的面积,用三角形面积的2倍除以斜边的长度即可求出斜边上的高。
2.C
解:28÷2-8=6(厘米),面积:8×6=48(平方厘米)。
故答案为:C。
用长方形的周长除以2求出长与宽的和,用长与宽的和减去长求出宽,用长乘宽求出平行四边形的面积即可。
3.D
解:三个连续的非零自然数的积一定既是偶数又是合数。
故答案为:D。
三个连续非零自然数一定至少有1个偶数,则这三个数的乘积就一定是偶数且不是2,那么这个乘积又是合数。
4.C
解:峨眉山万年寺二月份某天的气温波动范围是﹣2℃~7℃,万年寺这天的最高气温与最低气温相差9℃。
故答案为:C。
-2℃表示比0℃低2℃,7℃表示比0℃高7℃,把2和7相加就是最高气温与最低气温相差的温度。
5.B
解:31+29+31=91(天)
故答案为:B。
2024年是闰年,闰年2月29天,1月和3月都是31天,把这三个月的天数相加就是第一季度的总天数。
6.D
解:A:999不是2、5的倍数;
B:995不是2、3的倍数;
C:998不是3、5的倍数;
D:990是同时是2、3、5的倍数。
故答案为:D。
同时是2、3、5倍数的数的数的末位数字一定是0,且各个数位上数字之和是3的倍数。
7.C
解:3.14×(20÷2)2×3÷÷(3.14×52)
=3.14×100×3÷÷78.5
=2826÷78.5
=36(厘米)
故答案为:C。
这个圆锥高=下降水的体积×3÷底面积;其中,下降水的体积=π×半径2×高。
8.B
解:解:<1,★×<★;★÷>★;÷★≤;★×1=★;所以结果最大的是★÷。
故答案为:B。
一个非0数除以一个大于1的数,商小于被除数;一个非0数乘一个小于1的数,积小于这个数;根据计算规律判断得数的大小即可。
9.C
解:1:(1+100)=1:101;
故答案为:C。
药粉与药水的质量比=药粉质量:(药粉+水)的质量;据此解答。
10.B
解:
3+2=5(个)
4+3=7(个)。
故答案为:B。
最少时,下面一层3个,第二、第三层各1个,共5个小正方体;
最多时,下面一层3个,第二层2个,第3层2个,共7个小正方体。
11.C
解:4×80=320(毫米)
320毫米=32厘米。
故答案为:C。
在图纸上的长度=图上距离×比例尺,然后单位换算。
12.A
解:4×1-3=1(个)
4×2-3=5(个)
4×3-3=9(个)
4×4-3=13(个)
4×5-3=17(个)······
4×n-3=(4n-3)(个)。
故答案为:A。
第n幅图的点数= (4n-3)个。
13.A
解:=,=,=,<<,所以a>b>c;
故答案为:A。
和相同,因此比较、、的大小,数越小的,与它相加的加数就越大;据此解答。
14.C
解:①×;
②÷;
③25%=,×25%=×;
④×。
故答案为:C。
①阴影部分表示把单位“1”平均分成4份,取其中的3份,然后把平均分成4份,取其中的1份;
②总路程=行驶的路程÷行驶的分率;
③阴影部分的面积=总面积×所占的分率;
④要求的长度=总长度×所占的分率。
15.B
解:①十拿九稳,形容事件发生很有把握,十分可靠;
②凤毛麟角,形容是极少情况;
③海枯石烂,形容概率非常低;
④万无一失,形容事件一定会发生。
按照事件发生的可能性大小,从高到低排列是④①②③。
故答案为:B。
分别写出各句成语发生的概率,然后比较大小。
16.B
解:两个完全一样的正方体拼成一个长方体后,表面积的总和减少了。
故答案为:B。
将正方体拼在一起后,会有面叠在一起,导致拼成的长方体的表面积比原来正方体小两个面的面积。
17.C
圆的面积=π×()2=π×直径2÷4=×直径2;圆的面积和直径的平方乘正比例,但是圆的面积与它的直径不成比例。
故答案为:C。
正比例:两种相关联的量,一种量变化,另一种量也随之变化,如果这两种量中相对应的的比值一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系;
反比例:两种相关联的量,一种量变化,另一种量也随之变化,如果这两种量中相对应的的乘积一定,这两种量就叫做成反比例的量,它们的关系就叫做反比例关系。
18.A
解:设正方形的边长是4a,那么甲中圆的半径是2a,乙中圆的半径是a;
甲中圆的面积=π×2a×2a=4πa2;乙中圆的面积=4×π×a×a=4πa2;
甲、乙用去的材料一样多,所以剩下的材料也一样多。
故答案为:A。
圆的面积=π×r2;设定正方形的边长,计算甲、乙用去材料的多少即可;甲是一个大圆,大圆的半径等于正方形边长的一半;乙是4个小圆,小圆的半径是正方形边长的。
19.C
解:180°-50°-50°=80°。
故答案为:C。
由于同一个圆的半径大小相等,所以三角形ABC是等腰三角形,且∠B和∠C是底角,根据三角形内角和是180°求∠1即可。
20.B
解:图上1厘米表示100米,书店在图上距离学校的位置要比邮局距离学校远,笑笑的比较合理。
故答案为:B。
图中是按“上北下南,左西右东”来规定方向的,图上距离1厘米表示实际距离100米,根据方向、距离确定位置。
21.C
解:①3分米,3分米,3分米;
②2分米,3分米,4分米;
③1分米,4分米,4分米;共3种不同的围法。
故答案为:C。
根据三角形的三边关系:两边之和大于第三边,进行解答。
22.A
解:由4×20与4×6可知一个因数是26,另一个因数的个位是4;
由10×20与10×6可知,另一个因数的十位是1,所以另一个因数是14;这个算式是26×14;
故答案为:A。
两位数乘两位数,用第一个因数分别与第二个因数的个位与十位相乘,再把两次乘得的积相加即可;据此解答。
23.B
解:选项A:5在465的个位,2278的在百位,不能直接相加;
选项B:5在3.59的十分位,2在1.2的十分位,可以直接相加;
选项C:与的分母不同,不能直接相加;
选项D:5是整数,2是的分子,不能直接相加;
故答案为:B。
整数与小数的加减法要注意相同数位相加减;异分母分数相加减,要先通分,再把分子相加减,分母不变;整数与分数相加减,先将整数转化成与分数分母相同的分数,再把分子相加减,分母不变;据此解答。
24.A
解:a表示所有自然数,那么2a一定能被2整除,即2a是偶数,那么2a+1一定是奇数;
故答案为:A。
不能被2整除的数是奇数;能被2整除的数是偶数;只有1和它本身两个因数的数是质数;除了1和它本身还有其他因数的的数是合数;据此解答。
25.D
解:选项A:每天看的页数×看的天数=总页数(一定),乘积一定,每天看的页数和看的天数成反比例;
选项B:底面积×高×=圆锥体积(一定),乘积一定,底面积和高成反比例;
选项C:已经修的米数+剩下的米数=总米数(一定),和一定,已经修的米数和剩下的米数不成比例;
选项D:=每单位长度的物体映出的影子的长度(一定),比值一定,每棵树的高度和它影子的长度成正比例;
故答案为:D。
两种相关联的量,比值一定,成正比例关系;乘积一定,成反比例关系;据此解答。
26.A
解:1×3×4=12(立方米)。
故答案为:A。
新的长方体体积比原来减少的体积=减少的长×原来的宽×原来的高。
27.C
解:30÷÷100000
=150000000÷100000
=1500(千米)。
故答案为:C。
成都到北京的实际距离=图上距离÷比例尺,然后单位换算。
28.B
解:圆周率π保留两位小数的近似数是3.14, 呈现了“ 周三径一 ”。
故答案为:B。
圆的周长总是圆的直径的3倍多一点。
29.D
解:A项:速度×时间=路程(一定),路程一定,行驶的速度与时间成反比例;
B项:一个数×它的倒数=1(一定),一个数与它的倒数成反比例;
C项:加数+加数=和,两个数的和一定,一个加数与另一个加数不成比例;
D项:三角形的面积×2÷高=底(一定),三角形的底一定,它的面积和高成正比例。
故答案为:D。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
30.B
解:这堆货物可能有9箱或10箱。
故答案为:B。
从上面看到的图形可以看出正方体放了4个位置;从正面看到的图形可以看出正方体的两个位置上各放了3个;从左面看到的图形可以看出正方体1个位置放了2个,第四个位置是1个或2个,据此解答。
31.A
解:50÷5+1
=10+1
=11(面)
11×2=22(面)
故答案为:A。
两端植树:总长÷株距=间隔数;间隔数+1=棵数,棵数×2=跑道两旁一共要插的彩旗数。
32.B
解:÷4=
-×2=-0.25。
故答案为:B。
m点表示的数是 ,则每格表示的数=÷所占的格数;n在0的左边,表示负数,2格的地方是-0.25。
33.A
解:2×5=10
2×5×3×7=210。
故答案为:A。
A和B的最大公因数=A和B公有的质因数相乘;A和B的最小公倍数=A和B公有的质因数×各自独有的质因数。
34.A
解:这个两个数是42。
故答案为:A。
最小的质数是2,最小的合数是4,这个两个数是42。
35.D
解: + =,里有15个 。
故答案为:D。
一个分数的分数单位就是分母分之一,它有分子个这样的分数单位。
36.D
解:表示的算式是 × 。
故答案为:D。
表示长方形被平均分成3份,其中的2份涂色;表示涂色部分又被平均分成5份,其中的4份涂色。
37.A
解:已知a×50%=b×=c÷0.25。
a×0.5=b×0.8=c×4,
因为0.5<0.8<4,
所以a>b>c 。
故答案为:A。
积相等时,一个因数越小,另一个因数就越大,据此解答。
38.B
解:6×8÷4.8=48÷4.8=10(厘米)
6+8+10=24(厘米)
故答案为:B。
直角三角形两天直角边的积=底边×底边上的高,据此求出底边。
39.B
解:1+4×100=401(根)
故答案为:B。
规律:搭1间房子,需要小棒1+4=5(根);
搭2间房子,需要小棒1+4×2=9(根);
搭3间房子,需要小棒1+4×3=13(根);
......
搭n间房子,需要小棒1+4×n=1+4n(根)。
40.B
解:把x,y同时扩大到原来的10倍后,商不变,余数扩大10倍。
故答案为:B。
商不变性质:被除数和除数同时扩大或缩小相同的倍数(0除外),商不变;
商不变性质中余数变化规律:除数、被除数扩大或缩小几倍,余数就扩大或缩小几倍。
41.D
解:小军和小红两人的身高,不能确定。
故答案为:D。
平均数比最小的数大一些,比最大的数小一些,在它们之间;平均数反映的是一组数据的特征,不是其中每一个数据的特征,所以小军和小红的身高,无法比较。
42.A
解:40÷4=10(厘米)
(4-1)×2
=3×2
=6(个)
72÷6×10
=12×10
=120(立方厘米)。
故答案为:A。
原来每个小圆柱的体积=每个小圆柱的底面积×每个小圆柱的高,其中,每个小圆柱的底面积=减少的表面积÷减少面的个数,每个小圆柱的高=大圆柱的高÷4。
43.D
解:现价是原价的70%。
故答案为:D。
几折就表示十分之几,也就是百分之几十。
44.C
解:以大树为起点向西走8m记作﹣8m 。
故答案为:C。
以大树为起点向东走记作正数,向西走记作负数。
45.D
解:15千米=1500000厘米
3:1500000
=(3÷3):(1500000÷3)
=1:500000;
故答案为:D。
根据比例尺=图上距离:实际距离,代入数值计算解答。
46.A
解:500÷90%≈555.6(元)
500+500÷100×10
=500+5×10
=500+50
=550(元)
555.6元>550元。
故答案为:A。
妈妈准备花掉500元钱,到甲店买到商品的金额=500÷折扣;到乙店买到商品的金额=500+赠送的购物券金额,然后比较大小。
47.D
解:(-)÷
=÷
=。
故答案为:D。
工作效率提高的分率=(实际的工作效率-计划的工作效率) ÷计划的工作效率。
小升初数学备考真题分类汇编(四川地区专版)
试卷说明:
本试卷试题精选自四川各市,县2024、2023近两年六年级下学期小升初期末真题试卷,难易度均衡,适合四川各市,县的六年级学生小升初择校考、分班考等复习备考使用!
一、单选题
1.(2024·乐山)—个直角三角形的三条边长分别为3cm、4cm和5cm,这个三角形斜边上的高是( )
A.3cm B.6cm C.5cm D.2.4cm
2.(2024·乐山)将一个底边是8厘米的平行四边形沿高剪开,再拼成一个长方形,量得长方形的周长是28厘米,那么平行四边形的面积应该是( )平方厘米。
A.80 B.64 C.48 D.40
3.(2024·乐山)三个连续的非零自然数的积一定( )
A.既是奇数又是合数。 B.既是偶数又是质数。
C.既是奇数又是质数。 D.既是偶数又是合数。
4.(2024·乐山)峨眉山万年寺二月份某天的气温波动范围是﹣2℃~7℃,万年寺这天的最高气温与最低气温相差( )
A.5℃ B.﹣5℃ C.9℃ D.﹣9℃
5.(2024·乐山)2024年是新中国成立75周年,这一年的第一季度有( )天。
A.90 B.91 C.89 D.92
6.(2024·乐山)一个三位数,同时是2、3、5的倍数,这个数最大是( )
A.999 B.995 C.998 D.990
7.(2023·温江)把一个底面半径是5厘米的圆锥,完全浸没在一个底面直径是20厘米的圆柱形水槽中(如下图),取出圆锥后,水面下降了3厘米,这个圆锥高( )cm。
A.6 B.12 C.36 D.48
8.(2024·乐山)如果★代表一个非零自然数,那么下列式子中,结果最大的是( )
A.★× B.★÷ C.÷★ D.★×1
9.(2023·旌阳)把一克药粉放入100克水中,药粉与药水的质量比是( )
A.1:100 B.1:99 C.1:101 D.100:101
10.(2024·成都)在“观察物体”的课堂上,数学老师要求同学们搭出从以下两个方向看到的立体图形,那么同学们最少需要____个正方体,最多可以用____个正方体。 ( )
A.4和7 B.5和7 C.4和6 D.5和6
11.(2024·成都)一个微型零件长4mm,按80:1的比画在图纸上,在图纸上的长度是 ( )cm.
A.0.32 B.3.2 C.32 D.320
12.(2024·成都)认真观察下面这组图,第一幅图的点数为1,第2幅图的点数为5……
按照上面的规律,第n幅图的点数为 ( )
A.4n﹣3 B.4n+3 C.6n﹣2 D.6n+4
13.(2023·旌阳)已知,那么a、b、c的大小关系是( )
A.a>b>c B.b>a>c C.c>b>a D.b>c>a
14.(2024·成都)如图所示能用“表示或解决”的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
15.(2024·成都)下面的成语中,按照事件发生的可能性大小,从高到低排列正确的是 ( )
①十拿九稳 ②凤毛麟角 ③海枯石烂 ④万无一失
A.①②③④ B.④①②③ C.③④①② D.②③④①
16.(2023·新都)两个完全一样的正方体拼成一个长方体后,表面积的总和( )
A.增加了 B.减少了 C.不变 D.消失了
17.(2023·新都)一个圆的面积与它的直径( )
A.成正比例 B.成反比例 C.不成比例 D.无关联
18.(2023·新都)如图,在边长相等的两个正方形内剪圆片,比较剩下的材料,( )
A.甲、乙剩下一样多 B.甲剩下多
C.乙剩下多 D.无法确定
19.(2023·新都)如图,A为圆心,已知∠2=50度,则∠1=( )度。
A.100 B.90 C.80 D.60
20.(2023·新都)超市在学校正北面200米,邮局在学校正西面100米,书店在学校正东面300米。下面淘气和笑笑画的位置图相比,( )
A.淘气的较合理 B.笑笑的较合理
C.都不合理 D.都合理
21.(2023·旌阳)小明想把一根 9分米长的木条截成三段(每段的长度都是整分米数)围成一个三角形,有( )种不同的围法。
A.1 B.2 C.3 D.4
22.(2023·旌阳)如图可以表示算式( )
4×20 4×6
10×20 10×6
A.26×14 B.24×16 C.46×24 D.42×16
23.(2023·旌阳)下面的四个算式中“5”和“2”可以直接相加减的是( )
A.465+278 B.3.59﹣1.2 C. D.
24.(2023·旌阳)当a表示所有自然数0,1,2,3,4,5,……时,2a+1肯定表示( )
A.奇数 B.偶数 C.质数 D.合数
25.(2023·旌阳)下面四组相关联的量中,成正比例的是( )
A.看一本书,每天看的页数和看的天数
B.圆锥的体积一定。它的底面积和高
C.修一条路,已经修的米数和剩下的米数
D.同一时间、地点,每棵树的高度和它影子的长度
26.(2023·温江)一个长方体长、宽、高分别是5米、4米、3米,把它的长减少1米后,新的长方体体积比原来减少( )立方米
A.12 B.15 C.20 D.48
27.(2023·温江)在一幅比例尺是1:5000000的地图上,量得成都到北京的距离约是30厘米,成都到北京的实际距离约是( )千米。
A.15 B.150 C.1500 D.15000
28.(2023·温江)在2000年前我国古代名著《周髀算经》中,关于圆的周长与直径的关系有这样的记载:“周三径一”。下面呈现了“周三径一”的是( )
A. B.
C. D.
29.(2023·温江)下面各项中,两个量成正比例的是( )
A.路程一定,行驶的速度与时间
B.一个数与它的倒数
C.两个数的和一定,一个加数与另一个加数
D.三角形的底一定,它的面积和高
30.(2023·阆中)仓库的角落里有一堆存放货物的正方体纸箱,从三个不同方位看到的形状图如图,这堆货物可能有( )箱。
A.8 B.10 C.11 D.15
31.(2023·阆中)在学校一条长50米的跑道两旁,从头到尾每隔5米插一面彩旗,一共要插( )面彩旗。
A.22 B.20 C.11 D.10
32.(2023·温江)如图,如果m点表示的数是,则n点表示的数是( )
A.﹣2 B.﹣0.25 C.﹣0.125 D.
33.(2023·温江)如果A=2×3×5,B=2×5×7,那么A和B的最大公因数和最小公倍数分别是( )
A.10和210 B.15和30 C.25和100 D.35和70
34.(2023·温江)一个两位数,个位上是最小的质数,十位上是最小的合数( )
A.42 B.12 C.21 D.24
35.(2023·阆中) + 的和里有( )个 。
A.1 B.3 C.9 D.15
36.(2023·叙永)如图表示的算式是( )
A. ×10 B. ×8 C. × D. ×
37.(2023·叙永)已知a×50%=b×=c÷0.25(a,b,c均不为0),则a,b,c的大小关系是( )
A.a>b>c B.b>c>a C.c>a>b D.a<b<c
38.(2023·阆中)一个直角三角形的两条直角边AB=6 厘米和AC=8 厘米,斜边BC上的高是4.8厘米,那么三角形ABC的周长是( )厘米。
A.18.8 B.24 C.28.8 D.48
39.(2023·阆中)如图这样用小棒搭了3间房子,那么搭100间需要用( )根小棒。
A.400 B.401 C.500 D.501
40.(2023·阆中)在算式x÷y=10……7,把x,y同时扩大到原来的10倍后,商和余数分别是( )
A.10和7 B.10和70 C.100和7 D.100和70
41.(2023·阆中)小军班同学的平均身高是142厘米,小红班同学的平均身高是146厘米,若比较小军和小红两人的身高,则( )
A.小军高 B.小红高 C.一样高 D.不能确定
42.(2023·成都模拟)四个同样大小的圆柱拼成一个高为40cm的大圆柱时 ,表面积减少了72cm2 ,原来每个小圆柱的体积是( ) cm3。
A.120 B.360 C.480 D.720
43.(2023·阆中)商店搞促销活动,所有春装打七折出售,现价是原价的( )
A.3% B.7% C.30% D.70%
44.(2023·阆中)把小丽以大树为起点向东走10m记作+10m,小丽以大树为起点向西走8m记作( )
A.﹣10m B.+10m C.﹣8m D.+8m
45.(2023·旌阳)图书馆到学校的实际距离是15km,在一幅地图上量得这两地的距离是3cm,这幅图的比例尺是( )
A.1:5 B.1:5000 C.1:50000 D.1:500000
46.(2023·成都模拟)“五一”大假,甲、乙两个店各推出促销措施,甲店九折优惠,乙店购买100元货物赠送价值10元的购物券一张,妈妈准备花掉500元钱,去( ) 店更优惠。
A.甲 B.乙 C.甲、乙任选 D.无法比较
47.(2023·成都模拟)一件工作原计划6天完成,实际5天就完工,工作效率提高了( )。
A. B. C. D.
答案解析部分
1.D
解:3×4÷2×2÷5=2.4(cm)
故答案为:D。
三角形面积=底×高÷2,直角三角形两条直角边分别为三角形的底和高,根据两条直角边的长度求出三角形的面积,用三角形面积的2倍除以斜边的长度即可求出斜边上的高。
2.C
解:28÷2-8=6(厘米),面积:8×6=48(平方厘米)。
故答案为:C。
用长方形的周长除以2求出长与宽的和,用长与宽的和减去长求出宽,用长乘宽求出平行四边形的面积即可。
3.D
解:三个连续的非零自然数的积一定既是偶数又是合数。
故答案为:D。
三个连续非零自然数一定至少有1个偶数,则这三个数的乘积就一定是偶数且不是2,那么这个乘积又是合数。
4.C
解:峨眉山万年寺二月份某天的气温波动范围是﹣2℃~7℃,万年寺这天的最高气温与最低气温相差9℃。
故答案为:C。
-2℃表示比0℃低2℃,7℃表示比0℃高7℃,把2和7相加就是最高气温与最低气温相差的温度。
5.B
解:31+29+31=91(天)
故答案为:B。
2024年是闰年,闰年2月29天,1月和3月都是31天,把这三个月的天数相加就是第一季度的总天数。
6.D
解:A:999不是2、5的倍数;
B:995不是2、3的倍数;
C:998不是3、5的倍数;
D:990是同时是2、3、5的倍数。
故答案为:D。
同时是2、3、5倍数的数的数的末位数字一定是0,且各个数位上数字之和是3的倍数。
7.C
解:3.14×(20÷2)2×3÷÷(3.14×52)
=3.14×100×3÷÷78.5
=2826÷78.5
=36(厘米)
故答案为:C。
这个圆锥高=下降水的体积×3÷底面积;其中,下降水的体积=π×半径2×高。
8.B
解:解:<1,★×<★;★÷>★;÷★≤;★×1=★;所以结果最大的是★÷。
故答案为:B。
一个非0数除以一个大于1的数,商小于被除数;一个非0数乘一个小于1的数,积小于这个数;根据计算规律判断得数的大小即可。
9.C
解:1:(1+100)=1:101;
故答案为:C。
药粉与药水的质量比=药粉质量:(药粉+水)的质量;据此解答。
10.B
解:
3+2=5(个)
4+3=7(个)。
故答案为:B。
最少时,下面一层3个,第二、第三层各1个,共5个小正方体;
最多时,下面一层3个,第二层2个,第3层2个,共7个小正方体。
11.C
解:4×80=320(毫米)
320毫米=32厘米。
故答案为:C。
在图纸上的长度=图上距离×比例尺,然后单位换算。
12.A
解:4×1-3=1(个)
4×2-3=5(个)
4×3-3=9(个)
4×4-3=13(个)
4×5-3=17(个)······
4×n-3=(4n-3)(个)。
故答案为:A。
第n幅图的点数= (4n-3)个。
13.A
解:=,=,=,<<,所以a>b>c;
故答案为:A。
和相同,因此比较、、的大小,数越小的,与它相加的加数就越大;据此解答。
14.C
解:①×;
②÷;
③25%=,×25%=×;
④×。
故答案为:C。
①阴影部分表示把单位“1”平均分成4份,取其中的3份,然后把平均分成4份,取其中的1份;
②总路程=行驶的路程÷行驶的分率;
③阴影部分的面积=总面积×所占的分率;
④要求的长度=总长度×所占的分率。
15.B
解:①十拿九稳,形容事件发生很有把握,十分可靠;
②凤毛麟角,形容是极少情况;
③海枯石烂,形容概率非常低;
④万无一失,形容事件一定会发生。
按照事件发生的可能性大小,从高到低排列是④①②③。
故答案为:B。
分别写出各句成语发生的概率,然后比较大小。
16.B
解:两个完全一样的正方体拼成一个长方体后,表面积的总和减少了。
故答案为:B。
将正方体拼在一起后,会有面叠在一起,导致拼成的长方体的表面积比原来正方体小两个面的面积。
17.C
圆的面积=π×()2=π×直径2÷4=×直径2;圆的面积和直径的平方乘正比例,但是圆的面积与它的直径不成比例。
故答案为:C。
正比例:两种相关联的量,一种量变化,另一种量也随之变化,如果这两种量中相对应的的比值一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系;
反比例:两种相关联的量,一种量变化,另一种量也随之变化,如果这两种量中相对应的的乘积一定,这两种量就叫做成反比例的量,它们的关系就叫做反比例关系。
18.A
解:设正方形的边长是4a,那么甲中圆的半径是2a,乙中圆的半径是a;
甲中圆的面积=π×2a×2a=4πa2;乙中圆的面积=4×π×a×a=4πa2;
甲、乙用去的材料一样多,所以剩下的材料也一样多。
故答案为:A。
圆的面积=π×r2;设定正方形的边长,计算甲、乙用去材料的多少即可;甲是一个大圆,大圆的半径等于正方形边长的一半;乙是4个小圆,小圆的半径是正方形边长的。
19.C
解:180°-50°-50°=80°。
故答案为:C。
由于同一个圆的半径大小相等,所以三角形ABC是等腰三角形,且∠B和∠C是底角,根据三角形内角和是180°求∠1即可。
20.B
解:图上1厘米表示100米,书店在图上距离学校的位置要比邮局距离学校远,笑笑的比较合理。
故答案为:B。
图中是按“上北下南,左西右东”来规定方向的,图上距离1厘米表示实际距离100米,根据方向、距离确定位置。
21.C
解:①3分米,3分米,3分米;
②2分米,3分米,4分米;
③1分米,4分米,4分米;共3种不同的围法。
故答案为:C。
根据三角形的三边关系:两边之和大于第三边,进行解答。
22.A
解:由4×20与4×6可知一个因数是26,另一个因数的个位是4;
由10×20与10×6可知,另一个因数的十位是1,所以另一个因数是14;这个算式是26×14;
故答案为:A。
两位数乘两位数,用第一个因数分别与第二个因数的个位与十位相乘,再把两次乘得的积相加即可;据此解答。
23.B
解:选项A:5在465的个位,2278的在百位,不能直接相加;
选项B:5在3.59的十分位,2在1.2的十分位,可以直接相加;
选项C:与的分母不同,不能直接相加;
选项D:5是整数,2是的分子,不能直接相加;
故答案为:B。
整数与小数的加减法要注意相同数位相加减;异分母分数相加减,要先通分,再把分子相加减,分母不变;整数与分数相加减,先将整数转化成与分数分母相同的分数,再把分子相加减,分母不变;据此解答。
24.A
解:a表示所有自然数,那么2a一定能被2整除,即2a是偶数,那么2a+1一定是奇数;
故答案为:A。
不能被2整除的数是奇数;能被2整除的数是偶数;只有1和它本身两个因数的数是质数;除了1和它本身还有其他因数的的数是合数;据此解答。
25.D
解:选项A:每天看的页数×看的天数=总页数(一定),乘积一定,每天看的页数和看的天数成反比例;
选项B:底面积×高×=圆锥体积(一定),乘积一定,底面积和高成反比例;
选项C:已经修的米数+剩下的米数=总米数(一定),和一定,已经修的米数和剩下的米数不成比例;
选项D:=每单位长度的物体映出的影子的长度(一定),比值一定,每棵树的高度和它影子的长度成正比例;
故答案为:D。
两种相关联的量,比值一定,成正比例关系;乘积一定,成反比例关系;据此解答。
26.A
解:1×3×4=12(立方米)。
故答案为:A。
新的长方体体积比原来减少的体积=减少的长×原来的宽×原来的高。
27.C
解:30÷÷100000
=150000000÷100000
=1500(千米)。
故答案为:C。
成都到北京的实际距离=图上距离÷比例尺,然后单位换算。
28.B
解:圆周率π保留两位小数的近似数是3.14, 呈现了“ 周三径一 ”。
故答案为:B。
圆的周长总是圆的直径的3倍多一点。
29.D
解:A项:速度×时间=路程(一定),路程一定,行驶的速度与时间成反比例;
B项:一个数×它的倒数=1(一定),一个数与它的倒数成反比例;
C项:加数+加数=和,两个数的和一定,一个加数与另一个加数不成比例;
D项:三角形的面积×2÷高=底(一定),三角形的底一定,它的面积和高成正比例。
故答案为:D。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
30.B
解:这堆货物可能有9箱或10箱。
故答案为:B。
从上面看到的图形可以看出正方体放了4个位置;从正面看到的图形可以看出正方体的两个位置上各放了3个;从左面看到的图形可以看出正方体1个位置放了2个,第四个位置是1个或2个,据此解答。
31.A
解:50÷5+1
=10+1
=11(面)
11×2=22(面)
故答案为:A。
两端植树:总长÷株距=间隔数;间隔数+1=棵数,棵数×2=跑道两旁一共要插的彩旗数。
32.B
解:÷4=
-×2=-0.25。
故答案为:B。
m点表示的数是 ,则每格表示的数=÷所占的格数;n在0的左边,表示负数,2格的地方是-0.25。
33.A
解:2×5=10
2×5×3×7=210。
故答案为:A。
A和B的最大公因数=A和B公有的质因数相乘;A和B的最小公倍数=A和B公有的质因数×各自独有的质因数。
34.A
解:这个两个数是42。
故答案为:A。
最小的质数是2,最小的合数是4,这个两个数是42。
35.D
解: + =,里有15个 。
故答案为:D。
一个分数的分数单位就是分母分之一,它有分子个这样的分数单位。
36.D
解:表示的算式是 × 。
故答案为:D。
表示长方形被平均分成3份,其中的2份涂色;表示涂色部分又被平均分成5份,其中的4份涂色。
37.A
解:已知a×50%=b×=c÷0.25。
a×0.5=b×0.8=c×4,
因为0.5<0.8<4,
所以a>b>c 。
故答案为:A。
积相等时,一个因数越小,另一个因数就越大,据此解答。
38.B
解:6×8÷4.8=48÷4.8=10(厘米)
6+8+10=24(厘米)
故答案为:B。
直角三角形两天直角边的积=底边×底边上的高,据此求出底边。
39.B
解:1+4×100=401(根)
故答案为:B。
规律:搭1间房子,需要小棒1+4=5(根);
搭2间房子,需要小棒1+4×2=9(根);
搭3间房子,需要小棒1+4×3=13(根);
......
搭n间房子,需要小棒1+4×n=1+4n(根)。
40.B
解:把x,y同时扩大到原来的10倍后,商不变,余数扩大10倍。
故答案为:B。
商不变性质:被除数和除数同时扩大或缩小相同的倍数(0除外),商不变;
商不变性质中余数变化规律:除数、被除数扩大或缩小几倍,余数就扩大或缩小几倍。
41.D
解:小军和小红两人的身高,不能确定。
故答案为:D。
平均数比最小的数大一些,比最大的数小一些,在它们之间;平均数反映的是一组数据的特征,不是其中每一个数据的特征,所以小军和小红的身高,无法比较。
42.A
解:40÷4=10(厘米)
(4-1)×2
=3×2
=6(个)
72÷6×10
=12×10
=120(立方厘米)。
故答案为:A。
原来每个小圆柱的体积=每个小圆柱的底面积×每个小圆柱的高,其中,每个小圆柱的底面积=减少的表面积÷减少面的个数,每个小圆柱的高=大圆柱的高÷4。
43.D
解:现价是原价的70%。
故答案为:D。
几折就表示十分之几,也就是百分之几十。
44.C
解:以大树为起点向西走8m记作﹣8m 。
故答案为:C。
以大树为起点向东走记作正数,向西走记作负数。
45.D
解:15千米=1500000厘米
3:1500000
=(3÷3):(1500000÷3)
=1:500000;
故答案为:D。
根据比例尺=图上距离:实际距离,代入数值计算解答。
46.A
解:500÷90%≈555.6(元)
500+500÷100×10
=500+5×10
=500+50
=550(元)
555.6元>550元。
故答案为:A。
妈妈准备花掉500元钱,到甲店买到商品的金额=500÷折扣;到乙店买到商品的金额=500+赠送的购物券金额,然后比较大小。
47.D
解:(-)÷
=÷
=。
故答案为:D。
工作效率提高的分率=(实际的工作效率-计划的工作效率) ÷计划的工作效率。
同课章节目录
