2024-2025学年小升初数学备考真题分类汇编(云南地区专版)专题1 选择题(含解析)
文档属性
| 名称 | 2024-2025学年小升初数学备考真题分类汇编(云南地区专版)专题1 选择题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 360.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 07:43:52 | ||
图片预览



文档简介
专题1 选择题-2023-2024学年
小升初数学备考真题分类汇编(云南地区专版)
试卷说明:
本试卷试题精选自云南各市,县2024、2023近两年六年级下学期小升初期末真题试卷,难易度均衡,适合云南各市,县的六年级学生小升初择校考、分班考等复习备考使用!
一、单选题
1.(2024·祥云)甲、乙两人分别将一张长25.12cm,宽12.56cm的长方形纸以不同的方法围成一个圆柱(接头处不重叠),那么围成的两个圆柱的( )
A.高一定相等 B.侧面积一定相等
C.底面积一定相等 D.体积一定相等
2.(2024·昭通)张阿姨靠墙边围了一块梯形的菜地,围菜地的篱笆长35m。求这块菜地的面积,下面4位同学的算法或想法,正确的是( )
A.(8+12)×15÷2 B.(6+14)×15÷2
C.(35﹣15)×15÷2 D.不知道上、下底,无法计算
3.(2024·玉溪)如下图,两条平行线间有三个图形(单位:cm),比较它们的面积,( )
A.平行四边形面积最大 B.三角形面积最大
C.梯形面积最大 D.都相等
4.(2024·曲靖)把15÷7的结果化成小数,小数点后第2024位上的数是( )
A.2 B.8 C.1 D.4
5.(2024·官渡)如图,三个图形A、B、C的面积,按从小到大排列是( )
A.SA<SC<SB B.SC<SA<SB C.SA<SB<SC D.SC<SB<SA
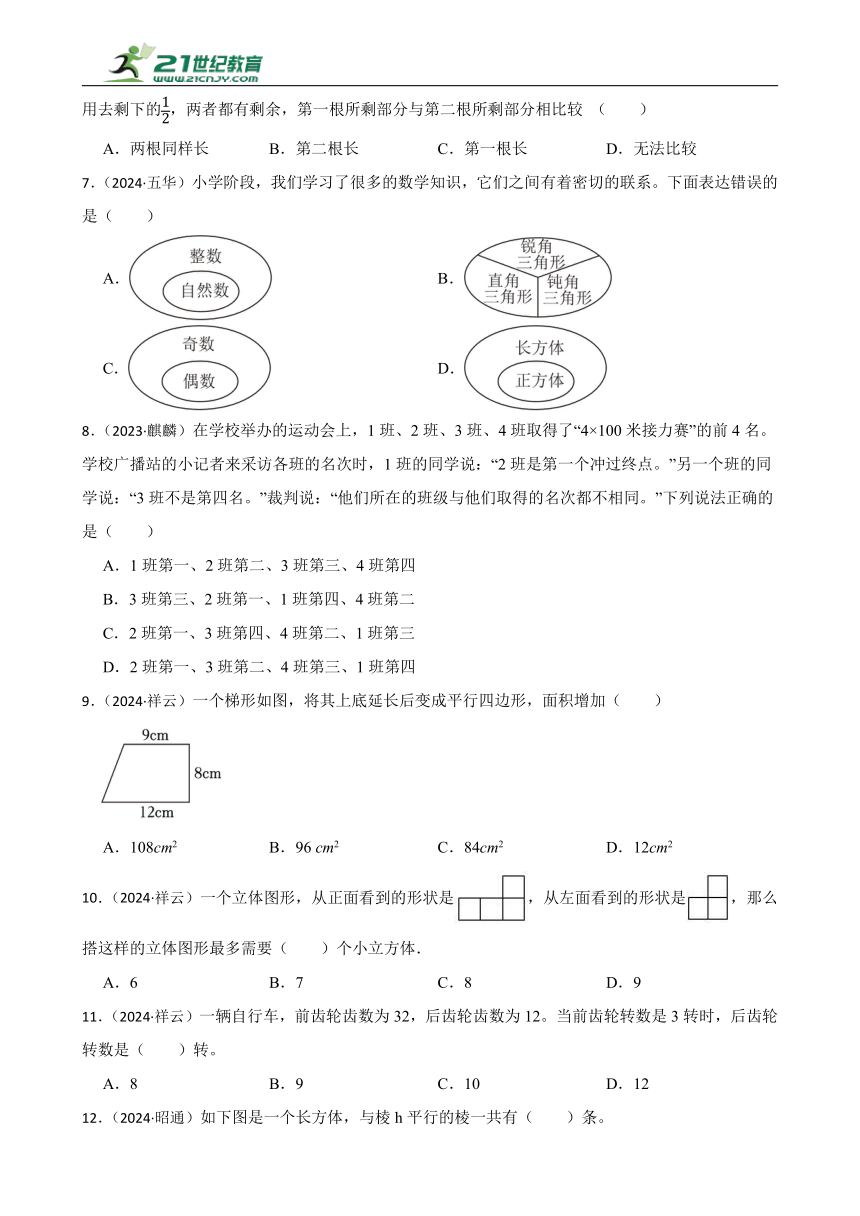
6.(2024·腾冲)有两根同样长的铁丝,从第一根中先用去,再用去米,从第二根中先用去米,再用去剩下的,两者都有剩余,第一根所剩部分与第二根所剩部分相比较 ( )
A.两根同样长 B.第二根长 C.第一根长 D.无法比较
7.(2024·五华)小学阶段,我们学习了很多的数学知识,它们之间有着密切的联系。下面表达错误的是( )
A. B.
C. D.
8.(2023·麒麟)在学校举办的运动会上,1班、2班、3班、4班取得了“4×100米接力赛”的前4名。学校广播站的小记者来采访各班的名次时,1班的同学说:“2班是第一个冲过终点。”另一个班的同学说:“3班不是第四名。”裁判说:“他们所在的班级与他们取得的名次都不相同。”下列说法正确的是( )
A.1班第一、2班第二、3班第三、4班第四
B.3班第三、2班第一、1班第四、4班第二
C.2班第一、3班第四、4班第二、1班第三
D.2班第一、3班第二、4班第三、1班第四
9.(2024·祥云)一个梯形如图,将其上底延长后变成平行四边形,面积增加( )
A.108cm2 B.96 cm2 C.84cm2 D.12cm2
10.(2024·祥云)一个立体图形,从正面看到的形状是,从左面看到的形状是,那么搭这样的立体图形最多需要( )个小立方体.
A.6 B.7 C.8 D.9
11.(2024·祥云)一辆自行车,前齿轮齿数为32,后齿轮齿数为12。当前齿轮转数是3转时,后齿轮转数是( )转。
A.8 B.9 C.10 D.12
12.(2024·昭通)如下图是一个长方体,与棱h平行的棱一共有( )条。
A.1 B.2 C.3 D.4
13.(2024·昭通) 8个小组研究事件发生的可能性,设计了如下活动:在装有红、黄两种颜色小球的盒子里摸球,每个小组盒子里装的球都一样。每次摸出一个球,记录下颜色,再放回摇匀,重复20次,结果如下。
小组 1 2 3 4 5 6 7 8 合计
摸出红球的次数 15 16 12 18 15 16 14 17 123
摸出黄球的次数 5 4 8 2 5 4 6 3 37
下面是四位同学根据统计结果作出的推断,说法错误的是( )
A.再接着摸一次,可能摸出红球,也可能摸出黄球。
B.红球个数一定比黄球多。
C.红球个数可能比黄球多。
D.如果每个小组再这样重复摸20次,那么摸出黄球的合计次数可能是40次。
14.(2024·昭通)m+13的和是偶数,那么m一定是( )
A.奇数 B.偶数 C.质数 D.合数
15.(2024·昭通)“小明玩射击游戏,全部射中。”可以用成语“百发百中”来形容,还可以用数学语言作出解释。下列数学语言解释正确的是( )
A.命中率是10% B.命中率是20%
C.命中率是50% D.命中率是100%
16.(2024·玉溪)下面的说法正确的有( )个。
①2024年第一季度有91天。
②在同一圆中,周长和半径成正比例。
③A在B的东偏北40°的方向上,也就是A在B的北偏东50°的方向上。
④任意两个等底等高的三角形都能拼成一个平行四边形。
⑤小数末尾添上0或者去掉0,小数的大小、意义、计数单位都不变。
⑥甲数的等于乙数的(甲、乙不相等且都大于0),甲、乙两数之比是5:7。
A.2 B.3 C.4 D.5
17.(2024·玉溪)施工队计划要修一段20千米的水渠,10天修了全长的。照这样计算,修完这段水渠共要多少天?下面是同学们的解答,你认为合理的有( )个。
小聪:20÷(20×÷10)=80(天)。
小明:1÷(÷10)=80(天)。
小智:10天修,20天修,30天修,70天修,80天修完全长。
小军:解:设修完这段水渠共需要x天,1:=x:10,x=80。
A.4 B.3 C.2 D.1
18.(2024·玉溪)用大小相同的小正方体摆成的物体,从正面看是,从上面看是,从左面看是( )
A. B. C. D.
19.(2024·曲靖)下列说法正确的是( )
A.平行四边形各边确定后,周长和面积就确定了。
B.三角形各边确定后,周长和面积就确定了。
C.……这列数的每一项越来越大,越来越接近1。
D.上述说法都不对。
20.(2024·曲靖) 一项工程,甲单独完成需要12天,乙单独完成需要8天。甲、乙的工作效率之比是( )
A.2:3 B.: C.8:12 D.:
21.(2024·曲靖)若a、b、c、d都是正数,且a×=b÷=c×0.7=d÷1.5,则a、b、c、d中最大的是( )
A.a B.b C.d D.c
22.(2024·曲靖)若一袋大米外包装上标有“净含量:(10±0.5)kg”,则下列包装的大米中不合格的是( )
A.10.3kg B.9.4kg C.10.5kg D.9.6kg
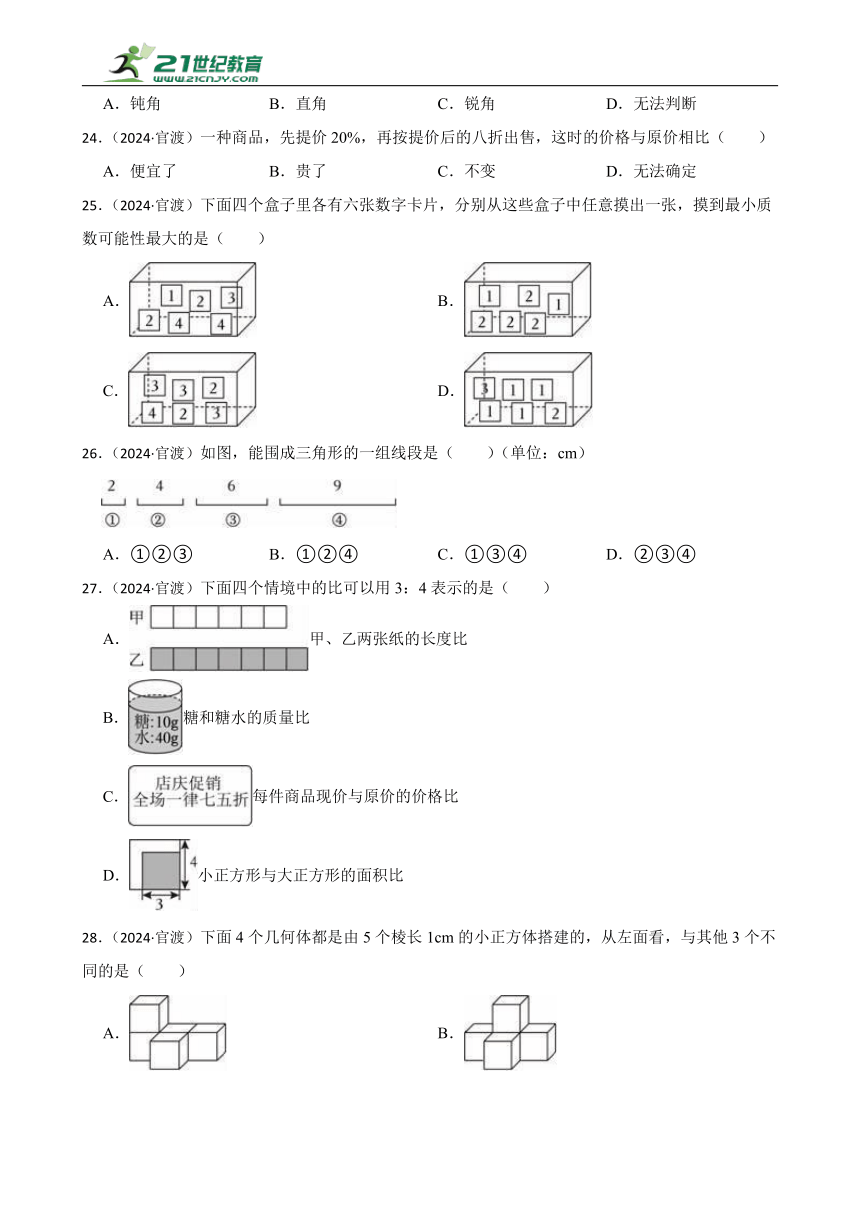
23.(2024·曲靖)已知一个等腰三角形顶角和底角的度数比是2:1,这个三角形是( )三角形。
A.钝角 B.直角 C.锐角 D.无法判断
24.(2024·官渡)一种商品,先提价20%,再按提价后的八折出售,这时的价格与原价相比( )
A.便宜了 B.贵了 C.不变 D.无法确定
25.(2024·官渡)下面四个盒子里各有六张数字卡片,分别从这些盒子中任意摸出一张,摸到最小质数可能性最大的是( )
A. B.
C. D.
26.(2024·官渡)如图,能围成三角形的一组线段是( )(单位:cm)
A.①②③ B.①②④ C.①③④ D.②③④
27.(2024·官渡)下面四个情境中的比可以用3:4表示的是( )
A.甲、乙两张纸的长度比
B.糖和糖水的质量比
C.每件商品现价与原价的价格比
D.小正方形与大正方形的面积比
28.(2024·官渡)下面4个几何体都是由5个棱长1cm的小正方体搭建的,从左面看,与其他3个不同的是( )
A. B.
C. D.
29.(2024·官渡)“0.5”这个数,在下面生活场景中使用最合适的是( )
A.一袋食盐的质量 B.一个书包的价钱
C.一本数学书封面的大小 D.珠穆朗玛峰的高度
30.(2024·官渡)下面的算式中,“8”和“5”能直接相加减的是( )
A.798+250 B.4.84﹣3.5 C.8+ D.
31.(2024·腾冲)好吃点餐馆用铁皮做一节圆柱形通风管,圆口的半径是0.2米,管长3米,接头处忽略不计,需要铁皮多少平方米?正确的算式是 ( )
A.3.14×0.2×3 B.2×3.14×0.2×3
C.3.14×0.22×3 D.2×3.14×0.2×3+3.14×0.2×2
32.(2024·腾冲)一个圆的周长是50.24厘米,半径减少3厘米,面积减少 ( )平方厘米。
A.78.5 B.50.24 C.200.96 D.122.46
33.(2024·腾冲)实验小学六年级“六 一”搞插花活动,把30束花插到7个花瓶中,总有一个花瓶中至少要插 ( )束花。
A.4 B.5 C.6 D.7
34.(2024·腾冲)下列说法中,正确的有 ( )个。
①正方体的棱长扩大到原来的2倍,体积扩大到原来的8倍。
②最小的偶数是2,最小的合数是4。
③a3一定比a2大。
④一个三角形的三个内角的度数之比是7:6:5,按角的分类,这是一个锐角三角形。
A.1 B.2 C.3 D.4
35.(2024·五华)饼干促销“买四盒送一盒”,妈妈买了四盒送了一盒,这相当于打几折?( )
A.二 B.五 C.七五 D.八
36.(2024·五华)下面的说法中,最合理的是( )
A.校运动会上东东跑100米用了10分钟
B.60个六年级学生的体重之和大约是1吨
C.一张身份证的面积是46cm2
D.乐乐每天喝250L的牛奶
37.(2024·五华)如果m÷n=a,那么数轴上a的位置正确的有可能是( )
A. B.
C. D.
38.(2024·五华)一把椅子a元,一张桌子的价格比它的2倍多4元,一张桌子的价格是( )
A.(2a+4)元 B.(2a﹣4)元 C.2(a+4)元 D.(a+2+4)元
39.(2023·红河)如果甲数的等于乙数的 (甲、乙两数均不为0),那么( )
A.甲=乙 B.甲<乙 C.甲>乙
40.(2023·红河)下列三条线段能围成三角形的是( )
A.3cm、4cm和5cm B.3cm、4cm和7cm C.3cm、4cm和1cm
41.(2023·红河)袋子里有5个红球,5个白球,任意摸出一个球( )
A.可能是红球 B.一定是红球 C.一定是白球
42.(2023·德宏)把一个高6dm、底面半径2dm的圆柱切成若干等份,拼成一个近似的长方体(如图),这时表面积( )
A.增加了24dm2 B.增加了12dm2 C.减少了24dm2 D.减少了12dm2
43.(2023·德宏)圆锥的底面半径扩大到原来的2倍,它的体积( )
A.不变 B.扩大到原来的2倍
C.缩小到原来的一半 D.扩大到原来的4倍
44.(2023·德宏)能与:组成比例的是( )
A.3:4 B.4:3 C.: D.3:
45.(2023·德宏) 一个圆的周长扩大到原来的3倍,它的面积就扩大到原来的( )倍。
A.3 B.6 C.9 D.12
46.(2023·麒麟)欢欢从家去商场给爸爸买生日礼物,走了一会儿,想起忘记带钱了,赶紧回家取钱再去商场,选好礼物付钱后回家,下面图( )反映出欢欢的这些情况。
A. B.
C. D.
47.(2023·麒麟)我们小学阶段学过一些平面图形,它们之间有着密切的联系。下列选项中,分别用集合图表示一些平面图形之间的关系,其中表示正确的是( )
A. B.
C. D.
48.(2023·麒麟)以下同题中,可以用8× 解决的( )
①爸爸以8千米/时的速度慢跑,他时跑了多少千米?
②一张长方形纸长8dm,宽dm,这张纸的周长是多少分米?
③聪聪做一个中国结用了m彩绳,做8个同样的中国结用了多少米彩绳?
④哥哥吃了8块饼干,妹妹吃的饼干数是哥哥的 ,妹妹吃了多少块饼干?
A.①③④ B.①③ C.② D.①②③④
49.(2023·麒麟)下列算式中,( )的计算结果正确。
A.1700÷400=4……1 B.3.6+ -3.6+ =0
C.1﹣0.12=0.9 D.201×49≈10000
50.(2023·麒麟)转动( )转盘的指针,落在三个区域的可能性相等。
A. B. C. D.
答案解析部分
1.B
解:围成的两个圆柱侧面积一定相等,都是等于长方形纸的面积。
故答案为:B。
用长方形纸围成圆柱体,侧面积等于长方形纸的面积。
2.C
解:上底和下底的长度和是(35-15)m,高是15m,所以正确的列式是(35﹣15)×15÷2。
故答案为:C。
这是一个直角梯形,高是15m,共3面是篱笆,所以用篱笆的长度减去高即可求出上底和下底的长度和,根据公式“梯形面积=(上底+下底)×高÷2”计算梯形面积。
3.D
解:假设平行线的之间的距离是h。
图一:400h;
图二:800×h÷2=400h;
图三:(200+600)h÷2=400h。
400h=400h=400h,面积相等。
故答案为:D。
平行线之间的距离处处相等,假设平行线的之间的距离是h。平行四边形的面积=底×高,三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,然后比较大小。
4.D
解:15÷7=
2024÷6=337(组)······2(位),则小数点后第2024位上的数是4。
故答案为:D。
这个循环小数的循环节是“142857”6个数字为一组循环,小数点后第2024位上的数循环了337组,剩余2位,则是4。
5.C
解:假设平行线之间的距离是1。
A的面积:(4+6)×1÷2=5;
B的面积:11×1÷2=5.5;
C的面积:6×1=6;
6>5.5>5, SA<SB<SC 。
故答案为:C。
平行线之间的距离相等,假设平行线之间的距离是1。梯形的面积=(上底+下底)×高÷2;三角形的面积=底×高÷2,平行四边形的面积=底×高,然后再比较大小。
6.B
解:两根铁丝都是用去了米,然后第一根又用去总长的,第二根又用去剩下的,则第二根剩下的长。
故答案为:B。
比较用去的长度,用去少的剩下的长。
7.C
解:A选项整数包括正数和负数和0,而自然数是0和正数,所以整数包括自然数,该选项正确;B选项三角形按角的大小分为锐角三角形、直角三角形、钝角三角形,所以三种三角形不存在包含关系,该选项正确;C选项整数中能被2整除的数是偶数,如2、4、6、8...不能被2整除的数是奇数,如1、3、5、...所以奇数和偶数不存在包含关系,该先项错误;D选项因为长方体的特征正方体都符合,比如相对的棱长度相等、相对的面完全相同等等,只不过正方体更特殊一些,它每条棱、每个面都一样,所以说它是特殊的长方体,该选项正确。
故答案为:C。
自然数是指用以计量事物的件数或表示事物次序的数如0,1,2,3,4...所表示的数。整数包括正数和负数和0,像-2,-1,0,1,2这样的数称为整数。整数中能被2整除的数是偶数,不能被2整除的数是奇数三角形按角的大小分为锐角三角形、直角三角形、纯角三角形。根据上述概念解答;长方体是由6个长方形(特殊青况有两个相对的面是正方形)围成的立体图形。在一个长方体中,相对的面完全相同,相对的棱长度相等。长方体有8个顶点,12条棱;正方体是由6个完全相同的正方形围成
的立体图形,正方体有8个顶点,12条棱,12条棱的长度都相等。
8.D
解:根据1班的同学说的知道2班第一。3班不是第四名,也不是第三名,所以3班是第二名。4班不是第四名,4班就是第三名。那么1班是第四名。
故答案为:D。
根据1班同学说的可以判断2班的名次。根据另一班同学说的和裁判说的可以判断3班的名次。然后分别判断1班和4班的名次即可。
9.D
解:
(12-9)×8÷2
=24÷2
=12(平方厘米)。
故答案为:D。
增加的面积=右侧三角形的面积=底×高÷2,其中,底=12-=9=3厘米,高=梯形的高。
10.B
解:
6+1=7(个)。
故答案为:B。
这个立体图形下面一层有6个小正方体,上面一层1个小正方体,共7个。
11.A
解:设后齿轮转数是x转。
32×3=12x
12x=96
x=96÷12
x=8
故答案为:A。
根据“前齿轮齿数×前齿轮转数=后齿轮齿数×后齿轮转数”,设后齿轮转数是x转,列出方程解方程即可。
12.C
解:图形是一个长方体,与棱h平行的棱一共有3条。
故答案为:C。
长方体共12条棱,分三组,4条长,4条宽,4条高。长方体相对的棱长度相等且平行。
13.B
解:共两种颜色的球,所以每次都有可能摸出红球或黄球;因为摸出红球次数都比黄球次数多,所以红球个数可能比黄球多,但不能确定红球个数一定比黄球多,所以“红球个数一定比黄球多”是错误的。
故答案为:B。
共两种颜色的球,那么任意一次都有可能摸出红球或黄球;摸出红球的次数多,所以红球可能比黄球多。
14.A
解:13是奇数,m+13的和是偶数,则m是奇数。
故答案为:A。
奇数是不能被2整除的数,偶数是能被2整除的数,奇数+奇数=偶数。
15.D
解:“百发百中”的意思就是命中率100%。
故答案为:D。
“百发百中”的意思就是每次都能命中,命中率为100%。
16.C
解:①2024÷4=506,31+29+31=91(天),原题干说法正确;
②圆的周长÷半径=π×2(一定),在同一圆中,周长和半径成正比例 ,原题干说法正确;
③90°-40°=50°,A在B的东偏北40°的方向上,也就是A在B的北偏东50°的方向上 ,原题干说法正确;
④任意两个完全一样的三角形都能拼成一个平行四边形 ,原题干说法错误;
⑤小数末尾添上0或者去掉0,小数的大小不变,意义、计数单位都变化了 ,原题干说法错误;
⑥甲:乙= : =5:7,原题干说法正确。
故答案为:C。
①2024年是闰年,2月29天,然后把1、2、3各月的天数相加;
②判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;
③在地图上的方位是上北,下南,左西,右东;东和西相对,南和北相对;西南和东北相对,西北和东南相对。描述路线图时,要先按行走路线确定每一个观测点,然后以每一个观测点为参照物,描述到下一个目标所的位置;
④任意两个完全一样的三角形都能拼成一个平行四边形,而非等底等高的三角形;
⑤小数的基本性质:在小数的末尾添上0或者去掉0,小数的大小不变,意义、计数单位都变化了 ;
⑥比例的基本性质:在比例里,两个内项积等于两个外项积。
17.A
解:小聪:根据求一个数的几分之几是多少,用这个数×几分之几,即用20×求出10天修了多少千米,再利用10天修的长度10天÷10,求出每天修多少千米,最后求出修完这段水渠共要多少天,20÷(20×÷10)=80(天),算法正确;
小明:把水渠的长度看作单位“1”,根据工作效率=工作总量÷工作时间;先用 ÷10,求出工作效率,再根据工作时间=工作总量÷工作效率,用1除以工作效率,求出修完这段水渠共要多少天,1÷( ÷10)=80(天),算法正确。
小智:利用修的天数与分率,得出修完这段水渠共要多少天,10天修 ,20天修,30天修,70天修,80天修完全长,算法正确。
小军:把这段水渠的长度看作单位"1";设修完这段水渠需要 x 天,根据工作总量:10天修的工作总量的分率比与工作总天数比已修的天数比不变;解:设修完这段水渠共需要 x 天,1: = x :10。得出 x =80;算法正确。
故答案为:A。
本题考查工程问题的应用,熟练掌握工作效率、工作时间和工作总量之间的关系解答本题。
18.A
解:这个立体图形有一层,前面一排3个正方形,后面一排一个正方形,并且中间对齐,从左面看是 。
故答案为:A。
先确定这个立体图形的形状,然后行左面看,看到一排两个正方形。
19.D
解:A项:平行四边形的面积与底和高有关,原题干说法错误;
B项:三角形的面积与底和高有关,原题干说法错误;
C项:这列数的每一项越来越小,离1越来越远, 原题干说法错误。
故答案为:D。
A项:平行四边形的面积=底×高;
B项:三角形的面积=底×高÷2;
C项:这列数的每一项越来越小,离1越来越远。
20.A
解:(1÷12):(1÷8)
=:
=2:3。
故答案为:A。
甲、乙的工作效率之比=(1÷甲的工作时间):(1÷乙的工作时间)。
21.A
解:a×=b÷=c×0.7=d÷1.5
a×=b×=c×0.7=d×
因为0.7>>>,所以a<b<d<c。
故答案为:A。
两个数相乘的积相等,较小的数要乘较大的数。
22.B
解:10-0.5=9.5(千克)
10+0.5=10.5(千克)
9.5千克≤合格的大米质量≤10.5千克,则9.4千克不合格。
故答案为:B。
合格的大米质量在9.5千克~10.5千克之间(包括9.5千克和10.5千克)。
23.B
解:180°÷(2+1+1)×2
=180°÷4×2
=45°×2
=90°,这个三角形是直角三角形。
故答案为:B。
等腰三角形的两个底角相等,这个三角形中最大内角的度数=三角形的内角和÷总份数×最大内角占的份数。
24.A
解:1×(1+20%)×80%
=120%×80%
=96%
96%<1,便宜了。
故答案为:A。
假设原价是1,现价=原价×(1+提价的百分率)×折扣,然后再比较大小。
25.B
解:A项:2÷6=;
B项:4÷6=;
C项:2÷6=;
D项:1÷6=;
>>。
故答案为:B。
最小的质数是2,摸到最小质数可能性=最小质数的个数÷数字总个数,然后比较大小。
26.D
解:A项:2+4=6(厘米)=6厘米, 不能围成三角形;
B项:2+4=6(厘米)<9厘米, 不能围成三角形;
C项:2+6=8(厘米)<9厘米, 不能围成三角形;
D项:4+6=10(厘米)>9厘米,能围成三角形。
故答案为:D。
三角形的任意两边之和大于第三边。
27.C
解:A:6:7;
B:10:(10+40)=1:5;
C:75%:1=3:4;
D:32:42=9:16。
故答案为:C。
A:甲直条的长度:乙直条的长度=6:7;
B:糖和糖水的质量比=糖的质量:(糖的质量+水的质量) ;
C:每件商品现价与原价的价格比=现价:原价;
D:小正方形与大正方形的面积比=小正方形边长2:大正方形边长2。
28.D
解:从左面看,依次是:
故答案为:D。
只有D项从左面看,看到两层,下面一层两个正方形,上面一层一个正方形,并且右侧对齐。
29.A
解:一袋食盐的质量是0.5千克,其余用“0.5”这个数都不合适。
故答案为:A。
根据实际生活经验以及题干中的具体数据来进行填空。
30.B
解:A项:798+250中“8”在个位上,“5”在十位上,不能直接相加减;
B项:4.84-3.5中“8”在十分位上,“5”在十分位上,能直接相加减;
C项:8+中“8”在个位上,“5”表示5个,不能直接相加减;
D项:-的分母不同,不能直接相加减。
故答案为:B。
只有在相同数位上、或者有相同的分数单位,这样的“8”和“5”才能直接相加减。
31.B
解:列式是:0.2×2×3.14×3。
故答案为:B。
需要铁皮的面积=侧面积=π×半径×2×通风管的长。
32.D
解:50.24÷3.14÷2
=16÷2
=8(厘米)
π×82-π×(8-3)2
=(64-25)×3.14
=39×3.14
=122.46(平方厘米)。
故答案为:D。
减少的面积=π×(原来半径2-现在半径2);其中,原来的半径=周长÷π÷2,现在的半径=原来的半径-3。
33.B
解:30÷7=4(束)······2(束)
4+1=5(束)。
故答案为:B。
抽屉原理,至少在同一抽屉里相同物体的个数=物体总个数÷抽屉的个数+1。
34.B
解:①2×2×2=8,体积扩大到原来的8倍,原题干说法正确;
②最小的偶数是0,最小的合数是4,原题干说法错误;
③ 13=1,12=1,a3不一定比a2大 ,原题干说法错误;
④180°÷(7+6+5)×7
=180°÷18×7
=10°×7
=70°,这个三角形是锐角三角形,原题干说法正确。
故答案为:B。
①正方体的体积=棱长×棱长×棱长,正方体的棱长扩大到原来的2倍,体积扩大到原来的8倍;
②最小的偶数是0,最小的合数是4;
③因为a的值不确定,则a3与a2无法确定大小;
④这个三角形中最大的内角度数=三角形的内角和÷总份数×最大内角占的份数,三角形中最大的内角是锐角,其余两个角也是锐角,这个三角形是锐角三角形。
35.D
解:4÷(4+1)
=4÷5
=0.8
=80%
=八折
故答案为:D。
根据题意,“买四送一”就是原来买4盒的价格,现在可以买4+1=5(盒),据此求出相当于打几折销售即可。
36.C
解:A选项校运动会上东东跑100米用了10秒,原题说法不符合实际;
B选项60个六年级学生的体重之和大约是2吨,原题说法不符合实际;
C选项一张身份证的面积是46cm2 ,原题说法符合实际;
D选项乐乐每天喝250mL的牛奶,原题说法不符合实际。
故答案为:C。
根据生活经验以及数据的大小,选择合适的计量单位,找出符合生活实际的即可解答。
37.D
解:
数轴上a的位置正确的有可能是 。
故答案为:D。
观察数轴,,,代入算式,除以一个数等于乘这个数的倒数,计算出的值即可,求值时,要先看字母等于几,再写出原式最后把数值代入式子计算。
38.A
解:一张桌子的价格是(2a+4)元。
故答案为:A。
用椅子的单价乘2,再加上4元,就是桌子的价格,据此可以解答。
39.C
解:甲数×=乙数× ,
因为< ,
所以甲数>乙数。
故答案为:C。
积相等,一个因数小的,另一个因数反而大。
40.A
解:3+4>5,3cm、4cm和5cm三条线段能围成三角形。
故答案为:A。
判断能不能围成三角形的方法:三角形两条短边之和必须大于第三边。
41.A
解:任意摸出一个球,可能是红球。
故答案为:A。
不确定事件也称可能事件,表明事件可能发生也可能不发生。
42.A
解:6×2×2
=12×2
=24(dm2);
故答案为:A。
拼成的长方体比原来的圆柱体增加了2个长为圆柱的高,宽为圆柱底面半径的长方形;据此计算解答。
43.D
解:原来圆锥的体积=π×半径2×高×;
扩大后圆锥的体积=π×(半径×2)2×高×
=4×π×半径2×高×;
体积扩大的倍数:(4×π×半径2×高×)÷(π×半径2×高×)=4;
故答案为:D。
圆锥的体积=π×半径2×高×,据此解答。
44.B
解::=÷=;
选项A:3:4=3÷4=;
选项B:4:3=4÷3=;
选项C::=÷=;
选项D:3:=3÷=12;
故答案为:B。
能组成比例的两组比的比值相等;计算出各个选项中的比,比值与 :的比值相等的就可以与:组成比例。
45.C
解:圆周长扩大到原来的3倍,那么圆半径也扩大到原来的3倍;
原来圆面积=π×半径2
扩大后圆面积=π×(半径×3)2
=9π×半径2;
(9π×半径2)÷(π×半径2)=9
故答案为:C。
圆周长=π×2×半径,圆周长扩大到原来的3倍,那么圆半径也扩大到原来的3倍;圆面积=π×半径2,据此计算出面积扩大的倍数。
46.B
解:A:没有表示出在商场购物的时间,不能反映这些情况;
B:能反映这些情况;
C:没有表示出返回家取钱的过程,不能反映这些情况;
D:返回时没有停留,没有表示出在商场购物的时间,不能反映这些情况。
故答案为:B。
横轴表示时间,纵轴表示离家的距离,在商场停留时时间向前,但是离家的距离不变。
47.B
解:A:直角梯形和等腰梯形都是梯形,直角梯形不是等腰梯形。表示错误;
B:表示正确;
C:只是按照角的大小分,不完整;
D:只是按照三角形的边分,不完整。
故答案为:B。
A:等腰梯形和直角梯形都是梯形;
B:平行四边形和梯形都是四边形,正方形是特殊的长方形,正方形和长方形都是特殊的平行四边形;
C、D:等腰三角形、等边三角形是按照三角形的边分,锐角三角形、直角三角形、钝角三角形是按照角的大小分。
48.A
解:①③④都可以用8×解决,②算式是(8+)×2。
故答案为:A。
①用慢跑的速度乘时间即可求出跑的长度;
②长方形周长=(长+宽)×2,根据公式列式计算;
③用一个中国节用彩绳的长度乘8即可求出做8个中国节用的长度;
④用哥哥吃的块数乘即可求出妹妹吃饼干的块数。
49.D
解:A:1700÷400=4……100,原来计算错误;
B:3.6+-3.6+=,原来计算错误;
C:1-0.12=0.99,原来计算错误;
D:201×49≈10000,计算正确。
故答案为:D。
A:商是4,用被除数减去商乘除数的积求出余数,余数是错误的;
B:把两个小数相减,把两个分数相加,或者按照从左到右的顺序计算;
C:0.12表示0.1×0.1,得数是0.01;
D:把201看作200,49看作50,这样估算出结果即可。
50.C
解:A、B、D,三个区域面积不相等,落在三个区域的可能性不相等。C三个区域的面积相等,落在三个区域的可能性相等。
故答案为:C。
要想落在三个区域的可能性相等,那么转盘上三个区域的面积要相等。
小升初数学备考真题分类汇编(云南地区专版)
试卷说明:
本试卷试题精选自云南各市,县2024、2023近两年六年级下学期小升初期末真题试卷,难易度均衡,适合云南各市,县的六年级学生小升初择校考、分班考等复习备考使用!
一、单选题
1.(2024·祥云)甲、乙两人分别将一张长25.12cm,宽12.56cm的长方形纸以不同的方法围成一个圆柱(接头处不重叠),那么围成的两个圆柱的( )
A.高一定相等 B.侧面积一定相等
C.底面积一定相等 D.体积一定相等
2.(2024·昭通)张阿姨靠墙边围了一块梯形的菜地,围菜地的篱笆长35m。求这块菜地的面积,下面4位同学的算法或想法,正确的是( )
A.(8+12)×15÷2 B.(6+14)×15÷2
C.(35﹣15)×15÷2 D.不知道上、下底,无法计算
3.(2024·玉溪)如下图,两条平行线间有三个图形(单位:cm),比较它们的面积,( )
A.平行四边形面积最大 B.三角形面积最大
C.梯形面积最大 D.都相等
4.(2024·曲靖)把15÷7的结果化成小数,小数点后第2024位上的数是( )
A.2 B.8 C.1 D.4
5.(2024·官渡)如图,三个图形A、B、C的面积,按从小到大排列是( )
A.SA<SC<SB B.SC<SA<SB C.SA<SB<SC D.SC<SB<SA
6.(2024·腾冲)有两根同样长的铁丝,从第一根中先用去,再用去米,从第二根中先用去米,再用去剩下的,两者都有剩余,第一根所剩部分与第二根所剩部分相比较 ( )
A.两根同样长 B.第二根长 C.第一根长 D.无法比较
7.(2024·五华)小学阶段,我们学习了很多的数学知识,它们之间有着密切的联系。下面表达错误的是( )
A. B.
C. D.
8.(2023·麒麟)在学校举办的运动会上,1班、2班、3班、4班取得了“4×100米接力赛”的前4名。学校广播站的小记者来采访各班的名次时,1班的同学说:“2班是第一个冲过终点。”另一个班的同学说:“3班不是第四名。”裁判说:“他们所在的班级与他们取得的名次都不相同。”下列说法正确的是( )
A.1班第一、2班第二、3班第三、4班第四
B.3班第三、2班第一、1班第四、4班第二
C.2班第一、3班第四、4班第二、1班第三
D.2班第一、3班第二、4班第三、1班第四
9.(2024·祥云)一个梯形如图,将其上底延长后变成平行四边形,面积增加( )
A.108cm2 B.96 cm2 C.84cm2 D.12cm2
10.(2024·祥云)一个立体图形,从正面看到的形状是,从左面看到的形状是,那么搭这样的立体图形最多需要( )个小立方体.
A.6 B.7 C.8 D.9
11.(2024·祥云)一辆自行车,前齿轮齿数为32,后齿轮齿数为12。当前齿轮转数是3转时,后齿轮转数是( )转。
A.8 B.9 C.10 D.12
12.(2024·昭通)如下图是一个长方体,与棱h平行的棱一共有( )条。
A.1 B.2 C.3 D.4
13.(2024·昭通) 8个小组研究事件发生的可能性,设计了如下活动:在装有红、黄两种颜色小球的盒子里摸球,每个小组盒子里装的球都一样。每次摸出一个球,记录下颜色,再放回摇匀,重复20次,结果如下。
小组 1 2 3 4 5 6 7 8 合计
摸出红球的次数 15 16 12 18 15 16 14 17 123
摸出黄球的次数 5 4 8 2 5 4 6 3 37
下面是四位同学根据统计结果作出的推断,说法错误的是( )
A.再接着摸一次,可能摸出红球,也可能摸出黄球。
B.红球个数一定比黄球多。
C.红球个数可能比黄球多。
D.如果每个小组再这样重复摸20次,那么摸出黄球的合计次数可能是40次。
14.(2024·昭通)m+13的和是偶数,那么m一定是( )
A.奇数 B.偶数 C.质数 D.合数
15.(2024·昭通)“小明玩射击游戏,全部射中。”可以用成语“百发百中”来形容,还可以用数学语言作出解释。下列数学语言解释正确的是( )
A.命中率是10% B.命中率是20%
C.命中率是50% D.命中率是100%
16.(2024·玉溪)下面的说法正确的有( )个。
①2024年第一季度有91天。
②在同一圆中,周长和半径成正比例。
③A在B的东偏北40°的方向上,也就是A在B的北偏东50°的方向上。
④任意两个等底等高的三角形都能拼成一个平行四边形。
⑤小数末尾添上0或者去掉0,小数的大小、意义、计数单位都不变。
⑥甲数的等于乙数的(甲、乙不相等且都大于0),甲、乙两数之比是5:7。
A.2 B.3 C.4 D.5
17.(2024·玉溪)施工队计划要修一段20千米的水渠,10天修了全长的。照这样计算,修完这段水渠共要多少天?下面是同学们的解答,你认为合理的有( )个。
小聪:20÷(20×÷10)=80(天)。
小明:1÷(÷10)=80(天)。
小智:10天修,20天修,30天修,70天修,80天修完全长。
小军:解:设修完这段水渠共需要x天,1:=x:10,x=80。
A.4 B.3 C.2 D.1
18.(2024·玉溪)用大小相同的小正方体摆成的物体,从正面看是,从上面看是,从左面看是( )
A. B. C. D.
19.(2024·曲靖)下列说法正确的是( )
A.平行四边形各边确定后,周长和面积就确定了。
B.三角形各边确定后,周长和面积就确定了。
C.……这列数的每一项越来越大,越来越接近1。
D.上述说法都不对。
20.(2024·曲靖) 一项工程,甲单独完成需要12天,乙单独完成需要8天。甲、乙的工作效率之比是( )
A.2:3 B.: C.8:12 D.:
21.(2024·曲靖)若a、b、c、d都是正数,且a×=b÷=c×0.7=d÷1.5,则a、b、c、d中最大的是( )
A.a B.b C.d D.c
22.(2024·曲靖)若一袋大米外包装上标有“净含量:(10±0.5)kg”,则下列包装的大米中不合格的是( )
A.10.3kg B.9.4kg C.10.5kg D.9.6kg
23.(2024·曲靖)已知一个等腰三角形顶角和底角的度数比是2:1,这个三角形是( )三角形。
A.钝角 B.直角 C.锐角 D.无法判断
24.(2024·官渡)一种商品,先提价20%,再按提价后的八折出售,这时的价格与原价相比( )
A.便宜了 B.贵了 C.不变 D.无法确定
25.(2024·官渡)下面四个盒子里各有六张数字卡片,分别从这些盒子中任意摸出一张,摸到最小质数可能性最大的是( )
A. B.
C. D.
26.(2024·官渡)如图,能围成三角形的一组线段是( )(单位:cm)
A.①②③ B.①②④ C.①③④ D.②③④
27.(2024·官渡)下面四个情境中的比可以用3:4表示的是( )
A.甲、乙两张纸的长度比
B.糖和糖水的质量比
C.每件商品现价与原价的价格比
D.小正方形与大正方形的面积比
28.(2024·官渡)下面4个几何体都是由5个棱长1cm的小正方体搭建的,从左面看,与其他3个不同的是( )
A. B.
C. D.
29.(2024·官渡)“0.5”这个数,在下面生活场景中使用最合适的是( )
A.一袋食盐的质量 B.一个书包的价钱
C.一本数学书封面的大小 D.珠穆朗玛峰的高度
30.(2024·官渡)下面的算式中,“8”和“5”能直接相加减的是( )
A.798+250 B.4.84﹣3.5 C.8+ D.
31.(2024·腾冲)好吃点餐馆用铁皮做一节圆柱形通风管,圆口的半径是0.2米,管长3米,接头处忽略不计,需要铁皮多少平方米?正确的算式是 ( )
A.3.14×0.2×3 B.2×3.14×0.2×3
C.3.14×0.22×3 D.2×3.14×0.2×3+3.14×0.2×2
32.(2024·腾冲)一个圆的周长是50.24厘米,半径减少3厘米,面积减少 ( )平方厘米。
A.78.5 B.50.24 C.200.96 D.122.46
33.(2024·腾冲)实验小学六年级“六 一”搞插花活动,把30束花插到7个花瓶中,总有一个花瓶中至少要插 ( )束花。
A.4 B.5 C.6 D.7
34.(2024·腾冲)下列说法中,正确的有 ( )个。
①正方体的棱长扩大到原来的2倍,体积扩大到原来的8倍。
②最小的偶数是2,最小的合数是4。
③a3一定比a2大。
④一个三角形的三个内角的度数之比是7:6:5,按角的分类,这是一个锐角三角形。
A.1 B.2 C.3 D.4
35.(2024·五华)饼干促销“买四盒送一盒”,妈妈买了四盒送了一盒,这相当于打几折?( )
A.二 B.五 C.七五 D.八
36.(2024·五华)下面的说法中,最合理的是( )
A.校运动会上东东跑100米用了10分钟
B.60个六年级学生的体重之和大约是1吨
C.一张身份证的面积是46cm2
D.乐乐每天喝250L的牛奶
37.(2024·五华)如果m÷n=a,那么数轴上a的位置正确的有可能是( )
A. B.
C. D.
38.(2024·五华)一把椅子a元,一张桌子的价格比它的2倍多4元,一张桌子的价格是( )
A.(2a+4)元 B.(2a﹣4)元 C.2(a+4)元 D.(a+2+4)元
39.(2023·红河)如果甲数的等于乙数的 (甲、乙两数均不为0),那么( )
A.甲=乙 B.甲<乙 C.甲>乙
40.(2023·红河)下列三条线段能围成三角形的是( )
A.3cm、4cm和5cm B.3cm、4cm和7cm C.3cm、4cm和1cm
41.(2023·红河)袋子里有5个红球,5个白球,任意摸出一个球( )
A.可能是红球 B.一定是红球 C.一定是白球
42.(2023·德宏)把一个高6dm、底面半径2dm的圆柱切成若干等份,拼成一个近似的长方体(如图),这时表面积( )
A.增加了24dm2 B.增加了12dm2 C.减少了24dm2 D.减少了12dm2
43.(2023·德宏)圆锥的底面半径扩大到原来的2倍,它的体积( )
A.不变 B.扩大到原来的2倍
C.缩小到原来的一半 D.扩大到原来的4倍
44.(2023·德宏)能与:组成比例的是( )
A.3:4 B.4:3 C.: D.3:
45.(2023·德宏) 一个圆的周长扩大到原来的3倍,它的面积就扩大到原来的( )倍。
A.3 B.6 C.9 D.12
46.(2023·麒麟)欢欢从家去商场给爸爸买生日礼物,走了一会儿,想起忘记带钱了,赶紧回家取钱再去商场,选好礼物付钱后回家,下面图( )反映出欢欢的这些情况。
A. B.
C. D.
47.(2023·麒麟)我们小学阶段学过一些平面图形,它们之间有着密切的联系。下列选项中,分别用集合图表示一些平面图形之间的关系,其中表示正确的是( )
A. B.
C. D.
48.(2023·麒麟)以下同题中,可以用8× 解决的( )
①爸爸以8千米/时的速度慢跑,他时跑了多少千米?
②一张长方形纸长8dm,宽dm,这张纸的周长是多少分米?
③聪聪做一个中国结用了m彩绳,做8个同样的中国结用了多少米彩绳?
④哥哥吃了8块饼干,妹妹吃的饼干数是哥哥的 ,妹妹吃了多少块饼干?
A.①③④ B.①③ C.② D.①②③④
49.(2023·麒麟)下列算式中,( )的计算结果正确。
A.1700÷400=4……1 B.3.6+ -3.6+ =0
C.1﹣0.12=0.9 D.201×49≈10000
50.(2023·麒麟)转动( )转盘的指针,落在三个区域的可能性相等。
A. B. C. D.
答案解析部分
1.B
解:围成的两个圆柱侧面积一定相等,都是等于长方形纸的面积。
故答案为:B。
用长方形纸围成圆柱体,侧面积等于长方形纸的面积。
2.C
解:上底和下底的长度和是(35-15)m,高是15m,所以正确的列式是(35﹣15)×15÷2。
故答案为:C。
这是一个直角梯形,高是15m,共3面是篱笆,所以用篱笆的长度减去高即可求出上底和下底的长度和,根据公式“梯形面积=(上底+下底)×高÷2”计算梯形面积。
3.D
解:假设平行线的之间的距离是h。
图一:400h;
图二:800×h÷2=400h;
图三:(200+600)h÷2=400h。
400h=400h=400h,面积相等。
故答案为:D。
平行线之间的距离处处相等,假设平行线的之间的距离是h。平行四边形的面积=底×高,三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,然后比较大小。
4.D
解:15÷7=
2024÷6=337(组)······2(位),则小数点后第2024位上的数是4。
故答案为:D。
这个循环小数的循环节是“142857”6个数字为一组循环,小数点后第2024位上的数循环了337组,剩余2位,则是4。
5.C
解:假设平行线之间的距离是1。
A的面积:(4+6)×1÷2=5;
B的面积:11×1÷2=5.5;
C的面积:6×1=6;
6>5.5>5, SA<SB<SC 。
故答案为:C。
平行线之间的距离相等,假设平行线之间的距离是1。梯形的面积=(上底+下底)×高÷2;三角形的面积=底×高÷2,平行四边形的面积=底×高,然后再比较大小。
6.B
解:两根铁丝都是用去了米,然后第一根又用去总长的,第二根又用去剩下的,则第二根剩下的长。
故答案为:B。
比较用去的长度,用去少的剩下的长。
7.C
解:A选项整数包括正数和负数和0,而自然数是0和正数,所以整数包括自然数,该选项正确;B选项三角形按角的大小分为锐角三角形、直角三角形、钝角三角形,所以三种三角形不存在包含关系,该选项正确;C选项整数中能被2整除的数是偶数,如2、4、6、8...不能被2整除的数是奇数,如1、3、5、...所以奇数和偶数不存在包含关系,该先项错误;D选项因为长方体的特征正方体都符合,比如相对的棱长度相等、相对的面完全相同等等,只不过正方体更特殊一些,它每条棱、每个面都一样,所以说它是特殊的长方体,该选项正确。
故答案为:C。
自然数是指用以计量事物的件数或表示事物次序的数如0,1,2,3,4...所表示的数。整数包括正数和负数和0,像-2,-1,0,1,2这样的数称为整数。整数中能被2整除的数是偶数,不能被2整除的数是奇数三角形按角的大小分为锐角三角形、直角三角形、纯角三角形。根据上述概念解答;长方体是由6个长方形(特殊青况有两个相对的面是正方形)围成的立体图形。在一个长方体中,相对的面完全相同,相对的棱长度相等。长方体有8个顶点,12条棱;正方体是由6个完全相同的正方形围成
的立体图形,正方体有8个顶点,12条棱,12条棱的长度都相等。
8.D
解:根据1班的同学说的知道2班第一。3班不是第四名,也不是第三名,所以3班是第二名。4班不是第四名,4班就是第三名。那么1班是第四名。
故答案为:D。
根据1班同学说的可以判断2班的名次。根据另一班同学说的和裁判说的可以判断3班的名次。然后分别判断1班和4班的名次即可。
9.D
解:
(12-9)×8÷2
=24÷2
=12(平方厘米)。
故答案为:D。
增加的面积=右侧三角形的面积=底×高÷2,其中,底=12-=9=3厘米,高=梯形的高。
10.B
解:
6+1=7(个)。
故答案为:B。
这个立体图形下面一层有6个小正方体,上面一层1个小正方体,共7个。
11.A
解:设后齿轮转数是x转。
32×3=12x
12x=96
x=96÷12
x=8
故答案为:A。
根据“前齿轮齿数×前齿轮转数=后齿轮齿数×后齿轮转数”,设后齿轮转数是x转,列出方程解方程即可。
12.C
解:图形是一个长方体,与棱h平行的棱一共有3条。
故答案为:C。
长方体共12条棱,分三组,4条长,4条宽,4条高。长方体相对的棱长度相等且平行。
13.B
解:共两种颜色的球,所以每次都有可能摸出红球或黄球;因为摸出红球次数都比黄球次数多,所以红球个数可能比黄球多,但不能确定红球个数一定比黄球多,所以“红球个数一定比黄球多”是错误的。
故答案为:B。
共两种颜色的球,那么任意一次都有可能摸出红球或黄球;摸出红球的次数多,所以红球可能比黄球多。
14.A
解:13是奇数,m+13的和是偶数,则m是奇数。
故答案为:A。
奇数是不能被2整除的数,偶数是能被2整除的数,奇数+奇数=偶数。
15.D
解:“百发百中”的意思就是命中率100%。
故答案为:D。
“百发百中”的意思就是每次都能命中,命中率为100%。
16.C
解:①2024÷4=506,31+29+31=91(天),原题干说法正确;
②圆的周长÷半径=π×2(一定),在同一圆中,周长和半径成正比例 ,原题干说法正确;
③90°-40°=50°,A在B的东偏北40°的方向上,也就是A在B的北偏东50°的方向上 ,原题干说法正确;
④任意两个完全一样的三角形都能拼成一个平行四边形 ,原题干说法错误;
⑤小数末尾添上0或者去掉0,小数的大小不变,意义、计数单位都变化了 ,原题干说法错误;
⑥甲:乙= : =5:7,原题干说法正确。
故答案为:C。
①2024年是闰年,2月29天,然后把1、2、3各月的天数相加;
②判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;
③在地图上的方位是上北,下南,左西,右东;东和西相对,南和北相对;西南和东北相对,西北和东南相对。描述路线图时,要先按行走路线确定每一个观测点,然后以每一个观测点为参照物,描述到下一个目标所的位置;
④任意两个完全一样的三角形都能拼成一个平行四边形,而非等底等高的三角形;
⑤小数的基本性质:在小数的末尾添上0或者去掉0,小数的大小不变,意义、计数单位都变化了 ;
⑥比例的基本性质:在比例里,两个内项积等于两个外项积。
17.A
解:小聪:根据求一个数的几分之几是多少,用这个数×几分之几,即用20×求出10天修了多少千米,再利用10天修的长度10天÷10,求出每天修多少千米,最后求出修完这段水渠共要多少天,20÷(20×÷10)=80(天),算法正确;
小明:把水渠的长度看作单位“1”,根据工作效率=工作总量÷工作时间;先用 ÷10,求出工作效率,再根据工作时间=工作总量÷工作效率,用1除以工作效率,求出修完这段水渠共要多少天,1÷( ÷10)=80(天),算法正确。
小智:利用修的天数与分率,得出修完这段水渠共要多少天,10天修 ,20天修,30天修,70天修,80天修完全长,算法正确。
小军:把这段水渠的长度看作单位"1";设修完这段水渠需要 x 天,根据工作总量:10天修的工作总量的分率比与工作总天数比已修的天数比不变;解:设修完这段水渠共需要 x 天,1: = x :10。得出 x =80;算法正确。
故答案为:A。
本题考查工程问题的应用,熟练掌握工作效率、工作时间和工作总量之间的关系解答本题。
18.A
解:这个立体图形有一层,前面一排3个正方形,后面一排一个正方形,并且中间对齐,从左面看是 。
故答案为:A。
先确定这个立体图形的形状,然后行左面看,看到一排两个正方形。
19.D
解:A项:平行四边形的面积与底和高有关,原题干说法错误;
B项:三角形的面积与底和高有关,原题干说法错误;
C项:这列数的每一项越来越小,离1越来越远, 原题干说法错误。
故答案为:D。
A项:平行四边形的面积=底×高;
B项:三角形的面积=底×高÷2;
C项:这列数的每一项越来越小,离1越来越远。
20.A
解:(1÷12):(1÷8)
=:
=2:3。
故答案为:A。
甲、乙的工作效率之比=(1÷甲的工作时间):(1÷乙的工作时间)。
21.A
解:a×=b÷=c×0.7=d÷1.5
a×=b×=c×0.7=d×
因为0.7>>>,所以a<b<d<c。
故答案为:A。
两个数相乘的积相等,较小的数要乘较大的数。
22.B
解:10-0.5=9.5(千克)
10+0.5=10.5(千克)
9.5千克≤合格的大米质量≤10.5千克,则9.4千克不合格。
故答案为:B。
合格的大米质量在9.5千克~10.5千克之间(包括9.5千克和10.5千克)。
23.B
解:180°÷(2+1+1)×2
=180°÷4×2
=45°×2
=90°,这个三角形是直角三角形。
故答案为:B。
等腰三角形的两个底角相等,这个三角形中最大内角的度数=三角形的内角和÷总份数×最大内角占的份数。
24.A
解:1×(1+20%)×80%
=120%×80%
=96%
96%<1,便宜了。
故答案为:A。
假设原价是1,现价=原价×(1+提价的百分率)×折扣,然后再比较大小。
25.B
解:A项:2÷6=;
B项:4÷6=;
C项:2÷6=;
D项:1÷6=;
>>。
故答案为:B。
最小的质数是2,摸到最小质数可能性=最小质数的个数÷数字总个数,然后比较大小。
26.D
解:A项:2+4=6(厘米)=6厘米, 不能围成三角形;
B项:2+4=6(厘米)<9厘米, 不能围成三角形;
C项:2+6=8(厘米)<9厘米, 不能围成三角形;
D项:4+6=10(厘米)>9厘米,能围成三角形。
故答案为:D。
三角形的任意两边之和大于第三边。
27.C
解:A:6:7;
B:10:(10+40)=1:5;
C:75%:1=3:4;
D:32:42=9:16。
故答案为:C。
A:甲直条的长度:乙直条的长度=6:7;
B:糖和糖水的质量比=糖的质量:(糖的质量+水的质量) ;
C:每件商品现价与原价的价格比=现价:原价;
D:小正方形与大正方形的面积比=小正方形边长2:大正方形边长2。
28.D
解:从左面看,依次是:
故答案为:D。
只有D项从左面看,看到两层,下面一层两个正方形,上面一层一个正方形,并且右侧对齐。
29.A
解:一袋食盐的质量是0.5千克,其余用“0.5”这个数都不合适。
故答案为:A。
根据实际生活经验以及题干中的具体数据来进行填空。
30.B
解:A项:798+250中“8”在个位上,“5”在十位上,不能直接相加减;
B项:4.84-3.5中“8”在十分位上,“5”在十分位上,能直接相加减;
C项:8+中“8”在个位上,“5”表示5个,不能直接相加减;
D项:-的分母不同,不能直接相加减。
故答案为:B。
只有在相同数位上、或者有相同的分数单位,这样的“8”和“5”才能直接相加减。
31.B
解:列式是:0.2×2×3.14×3。
故答案为:B。
需要铁皮的面积=侧面积=π×半径×2×通风管的长。
32.D
解:50.24÷3.14÷2
=16÷2
=8(厘米)
π×82-π×(8-3)2
=(64-25)×3.14
=39×3.14
=122.46(平方厘米)。
故答案为:D。
减少的面积=π×(原来半径2-现在半径2);其中,原来的半径=周长÷π÷2,现在的半径=原来的半径-3。
33.B
解:30÷7=4(束)······2(束)
4+1=5(束)。
故答案为:B。
抽屉原理,至少在同一抽屉里相同物体的个数=物体总个数÷抽屉的个数+1。
34.B
解:①2×2×2=8,体积扩大到原来的8倍,原题干说法正确;
②最小的偶数是0,最小的合数是4,原题干说法错误;
③ 13=1,12=1,a3不一定比a2大 ,原题干说法错误;
④180°÷(7+6+5)×7
=180°÷18×7
=10°×7
=70°,这个三角形是锐角三角形,原题干说法正确。
故答案为:B。
①正方体的体积=棱长×棱长×棱长,正方体的棱长扩大到原来的2倍,体积扩大到原来的8倍;
②最小的偶数是0,最小的合数是4;
③因为a的值不确定,则a3与a2无法确定大小;
④这个三角形中最大的内角度数=三角形的内角和÷总份数×最大内角占的份数,三角形中最大的内角是锐角,其余两个角也是锐角,这个三角形是锐角三角形。
35.D
解:4÷(4+1)
=4÷5
=0.8
=80%
=八折
故答案为:D。
根据题意,“买四送一”就是原来买4盒的价格,现在可以买4+1=5(盒),据此求出相当于打几折销售即可。
36.C
解:A选项校运动会上东东跑100米用了10秒,原题说法不符合实际;
B选项60个六年级学生的体重之和大约是2吨,原题说法不符合实际;
C选项一张身份证的面积是46cm2 ,原题说法符合实际;
D选项乐乐每天喝250mL的牛奶,原题说法不符合实际。
故答案为:C。
根据生活经验以及数据的大小,选择合适的计量单位,找出符合生活实际的即可解答。
37.D
解:
数轴上a的位置正确的有可能是 。
故答案为:D。
观察数轴,,,代入算式,除以一个数等于乘这个数的倒数,计算出的值即可,求值时,要先看字母等于几,再写出原式最后把数值代入式子计算。
38.A
解:一张桌子的价格是(2a+4)元。
故答案为:A。
用椅子的单价乘2,再加上4元,就是桌子的价格,据此可以解答。
39.C
解:甲数×=乙数× ,
因为< ,
所以甲数>乙数。
故答案为:C。
积相等,一个因数小的,另一个因数反而大。
40.A
解:3+4>5,3cm、4cm和5cm三条线段能围成三角形。
故答案为:A。
判断能不能围成三角形的方法:三角形两条短边之和必须大于第三边。
41.A
解:任意摸出一个球,可能是红球。
故答案为:A。
不确定事件也称可能事件,表明事件可能发生也可能不发生。
42.A
解:6×2×2
=12×2
=24(dm2);
故答案为:A。
拼成的长方体比原来的圆柱体增加了2个长为圆柱的高,宽为圆柱底面半径的长方形;据此计算解答。
43.D
解:原来圆锥的体积=π×半径2×高×;
扩大后圆锥的体积=π×(半径×2)2×高×
=4×π×半径2×高×;
体积扩大的倍数:(4×π×半径2×高×)÷(π×半径2×高×)=4;
故答案为:D。
圆锥的体积=π×半径2×高×,据此解答。
44.B
解::=÷=;
选项A:3:4=3÷4=;
选项B:4:3=4÷3=;
选项C::=÷=;
选项D:3:=3÷=12;
故答案为:B。
能组成比例的两组比的比值相等;计算出各个选项中的比,比值与 :的比值相等的就可以与:组成比例。
45.C
解:圆周长扩大到原来的3倍,那么圆半径也扩大到原来的3倍;
原来圆面积=π×半径2
扩大后圆面积=π×(半径×3)2
=9π×半径2;
(9π×半径2)÷(π×半径2)=9
故答案为:C。
圆周长=π×2×半径,圆周长扩大到原来的3倍,那么圆半径也扩大到原来的3倍;圆面积=π×半径2,据此计算出面积扩大的倍数。
46.B
解:A:没有表示出在商场购物的时间,不能反映这些情况;
B:能反映这些情况;
C:没有表示出返回家取钱的过程,不能反映这些情况;
D:返回时没有停留,没有表示出在商场购物的时间,不能反映这些情况。
故答案为:B。
横轴表示时间,纵轴表示离家的距离,在商场停留时时间向前,但是离家的距离不变。
47.B
解:A:直角梯形和等腰梯形都是梯形,直角梯形不是等腰梯形。表示错误;
B:表示正确;
C:只是按照角的大小分,不完整;
D:只是按照三角形的边分,不完整。
故答案为:B。
A:等腰梯形和直角梯形都是梯形;
B:平行四边形和梯形都是四边形,正方形是特殊的长方形,正方形和长方形都是特殊的平行四边形;
C、D:等腰三角形、等边三角形是按照三角形的边分,锐角三角形、直角三角形、钝角三角形是按照角的大小分。
48.A
解:①③④都可以用8×解决,②算式是(8+)×2。
故答案为:A。
①用慢跑的速度乘时间即可求出跑的长度;
②长方形周长=(长+宽)×2,根据公式列式计算;
③用一个中国节用彩绳的长度乘8即可求出做8个中国节用的长度;
④用哥哥吃的块数乘即可求出妹妹吃饼干的块数。
49.D
解:A:1700÷400=4……100,原来计算错误;
B:3.6+-3.6+=,原来计算错误;
C:1-0.12=0.99,原来计算错误;
D:201×49≈10000,计算正确。
故答案为:D。
A:商是4,用被除数减去商乘除数的积求出余数,余数是错误的;
B:把两个小数相减,把两个分数相加,或者按照从左到右的顺序计算;
C:0.12表示0.1×0.1,得数是0.01;
D:把201看作200,49看作50,这样估算出结果即可。
50.C
解:A、B、D,三个区域面积不相等,落在三个区域的可能性不相等。C三个区域的面积相等,落在三个区域的可能性相等。
故答案为:C。
要想落在三个区域的可能性相等,那么转盘上三个区域的面积要相等。
同课章节目录
