2024-2025学年小升初数学备考真题分类汇编(云南地区专版)专题2 填空题(含解析)
文档属性
| 名称 | 2024-2025学年小升初数学备考真题分类汇编(云南地区专版)专题2 填空题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 207.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 07:44:47 | ||
图片预览




文档简介
专题1填空题-2023-2024学年
小升初数学备考真题分类汇编(云南地区专版)
试卷说明:
本试卷试题精选自云南各市,县2024、2023近两年六年级下学期小升初期末真题试卷,难易度均衡,适合云南各市,县的六年级学生小升初择校考、分班考等复习备考使用!
一、填空题
1.(2024·祥云)在0、2、3、6、7这五个数字中选取三个数字组成一个三位数,使它同时是2、3、5的倍数,这个数最大是 。
2.(2024·昭通)小明带了一些钱买文具,先用去所带钱的,又用去剩下钱的,这时还剩下10元。小明原来带了 元。
3.(2024·玉溪) 2022年6月17日我国第三艘航空母舰福建舰成功下水。据悉,它的长是320米,宽是78米,排水量8万余吨。如果按照一定的比例尺制成模型后,长是16厘米,这个模型的比例尺为 ,模型的宽应是 厘米。
4.(2024·曲靖)如下图,把一个高15cm的大圆柱切成3个相同的小圆柱,表面积增加了56cm2,那么原来大圆柱的体积是 cm3。
5.(2024·曲靖) 一幅地图的比例尺是1:8000000,把它改成线段比例尺是 ,已知AB两地的实际距离是240千米,在这幅地图上应画 厘米。
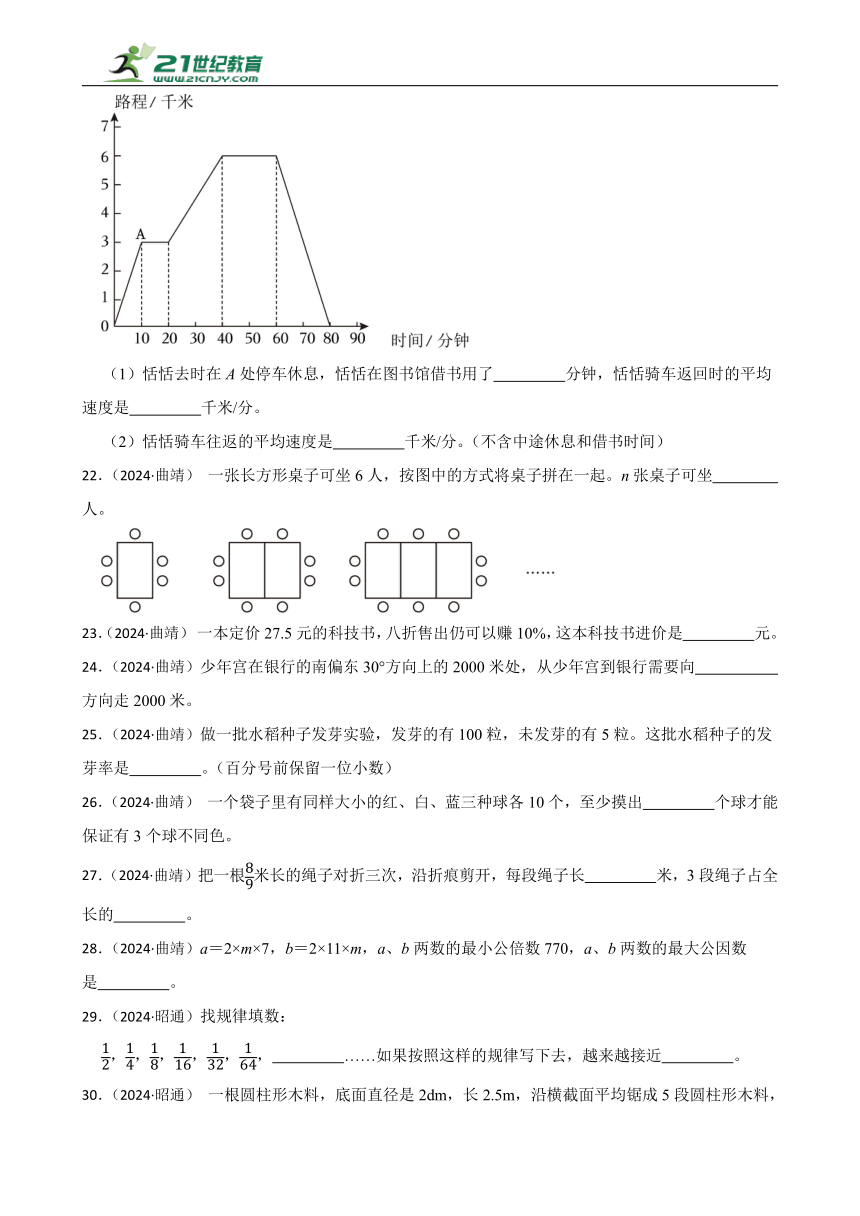
6.(2024·官渡)小明表演扑克牌“魔术”。一副扑克牌,取出大小王,还剩52张牌,9人每人随意抽1张,至少有 张牌是相同的花色。
7.(2024·官渡)一年中,北半球白昼时间最长的一天是“夏至”,黑夜时间最长的一天是“冬至”。2024年的夏至时间是6月21日,昆明这一天的白昼与黑夜的时间比大约是7:5,这一天昆明的白昼时间有 小时。
8.(2024·腾冲)昆明师大附小的一个篮球场的长是28米,宽是15米,把它画在比例尺是1:500的平面图上,篮球场的长在图上的距离是 厘米。图上篮球场的面积是 平方厘米。
9.(2024·腾冲)周末,冬冬一家开车去看望外婆,0.6小时行完全程的,照这样的速度,行完全程的,需要 小时。
10.(2024·五华)如果8x=7y(x,y均不为0),那么x:y= : 。
11.(2024·五华)在一幅比例尺是1:5000000的地图上量得昆明到大理的距离是6.8厘米,昆明到大理的实际距离是 千米。
12.(2024·五华)如图,如果“D”表示的数是24,则“A”表示的数是 ;如果“B”表示的数是,则“C”表示的数是 。
13.(2024·官渡)图中直角梯形②是直角梯形①沿对称轴画出的轴对称图形。根据图中的信息请用数对表示出点A的位置,A( , )。
14.(2024·官渡)= %=9÷ =24: = 。
15.(2024·官渡)数轴上A点表示的数是 ,D点表示的数是 。
16.(2024·官渡)昆明长水国际机场是我国八大区域性枢纽机场之一,2023年旅客吞吐量42033500人次,横线上的数读作 人次,约是 万人次(保留一位小数)。
17.(2024·腾冲)把一段长2米的圆柱形木材锯成4段小圆柱后,表面积总和比原来增加了18.84平方分米,那么原来这根木材的体积是 立方分米。
18.(2024·腾冲)把一根5分米长的绳子对折三次,每段是全长的 ,每段长 分米。
19.(2024·腾冲)今年我市进行污水工程改造,如果甲施工队单独施工需要24天完成,乙施工队单独施工需要36天完成,那么甲乙施工队的工作效率的最简单的整数比是 ,甲乙施工队合作施工,需要 天完成。
20.(2024·腾冲)一个三位小数,精确到百分位约是1.88,这个三位小数最小是 ,最大是 。
21.(2024·曲靖)恬恬骑车从家去相距6千米的图书馆借书,根据如图所示的统计图解决问题。
(1)恬恬去时在A处停车休息,恬恬在图书馆借书用了 分钟,恬恬骑车返回时的平均速度是 千米/分。
(2)恬恬骑车往返的平均速度是 千米/分。(不含中途休息和借书时间)
22.(2024·曲靖) 一张长方形桌子可坐6人,按图中的方式将桌子拼在一起。n张桌子可坐 人。
23.(2024·曲靖) 一本定价27.5元的科技书,八折售出仍可以赚10%,这本科技书进价是 元。
24.(2024·曲靖)少年宫在银行的南偏东30°方向上的2000米处,从少年宫到银行需要向 方向走2000米。
25.(2024·曲靖)做一批水稻种子发芽实验,发芽的有100粒,未发芽的有5粒。这批水稻种子的发芽率是 。(百分号前保留一位小数)
26.(2024·曲靖) 一个袋子里有同样大小的红、白、蓝三种球各10个,至少摸出 个球才能保证有3个球不同色。
27.(2024·曲靖)把一根米长的绳子对折三次,沿折痕剪开,每段绳子长 米,3段绳子占全长的 。
28.(2024·曲靖)a=2×m×7,b=2×11×m,a、b两数的最小公倍数770,a、b两数的最大公因数是 。
29.(2024·昭通)找规律填数:
,,,,,, ……如果按照这样的规律写下去,越来越接近 。
30.(2024·昭通) 一根圆柱形木料,底面直径是2dm,长2.5m,沿横截面平均锯成5段圆柱形木料,表面积增加了 dm2。
31.(2024·昭通)“六一”节,某书店的图书一律打八折销售。小军买了一本《趣味数学》,省了1.6元。这本书的原价是 元。
32.(2024·昭通) 一只蚂蚁和一只七星瓢虫同时从“0”出发,背向而行(如图,每小格代表1m)。行了8分钟,这时两只小虫相距11m,七星瓢虫在“5”处,小蚂蚁在 处。
33.(2024·昭通) 2023年云南旅游持续恢复回暖。云南省《政府工作报告》中指出,2023年,全省接待游客十亿四千二百万人次,旅游总收入达1.44万亿元。报告还指出,2024年云南将聚焦文化和旅游强省目标,让“有一种叫云南的生活”更加深入人心,旅游总收入力争突破1.5万亿元。横线上这个数写作 人次,省略亿位后面的尾数是 人次。
34.(2024·广州)12和18的最大公因数是 ,最小公倍数是 .
35.(2024·玉溪) 五一期间新平举办了“腌菜长街宴”,吸引了不少游客。长街宴就是将若干张桌子拼成长长的宴席(如图)。如果每张桌子每边坐2人,那么摆一张桌子可以坐8人,摆2张桌子可以坐12人,摆3张桌子可以坐16人,摆6张桌子可以坐 人,摆n张桌子可以坐 人。
36.(2024·玉溪) 六⑵班综合实践小队有16个孩子,他们至少有 个人的属相相同。
37.(2024·玉溪) 一个三角形三个内角度数比是4:4:1,这个三角形有 条对称轴;如果它两边的长分别是2厘米和5厘米,则它的周长为 厘米。
38.(2023·红河)一架飞机从昆明飞往北京,飞行的速度和时间成 比例。
39.(2023·红河)小东2022年升入七年级(4)班,他的座位号是16,学号是2022070416。同班的小亮座位号是32 。
40.(2023·德宏)把一个圆柱削成一个最大的圆锥,削去的体积是80cm3,则圆锥的体积是 cm3,圆柱的体积是 cm3。
41.(2023·德宏) 一件羊绒大衣的标签上写着:“80%羊毛,20%羊绒”。“80%羊毛”的含义是:这件羊绒大衣所含的 占这件羊绒大衣总成分的。
42.(2023·德宏)张叔叔得到一笔1000元的稿费。其中800元是免税的,其余部分按20%的税率缴税,张叔叔应缴税 元,税后收入是 元。
43.(2023·麒麟)如图,1张餐桌可坐4人,2张餐桌拼在一起可坐6人,3张餐桌拼在一起可坐8人。按照这样拼桌,6张餐桌可坐 人,n张餐桌可坐 人。
44.(2023·麒麟)长方形ABCD的长和宽分别是4cm和3cm,把它按2:1放大后得到长方形EFGH。长方形ABCD和长方形EFGH的周长之比是 ,面积之比是 。
45.(2023·麒麟)一个移动硬盘的存储量是mG,存储一部电影约需2G的内存量,存了n部电影,这个硬盘还剩 G的存储量;当m=512,n=20,还剩余 G的存储量。
46.(2023·麒麟)图中三角形ABD的面积是14.5cm2,平行四边形ABCE的面积是 cm2。
47.(2023·麒麟)已知 那么把x,y,z按从小到大的顺序排列是: 。
48.(2023·麒麟)已知 ,小数点后第50位上的数是 。
49.(2023·麒麟)一个数的千万位上是最小的合数,万位和千位上是最大的一位数,其余各位上都是最小的偶数,这个数写作: ,省略万位后面的尾数是 。
50.(2022·麒麟)水果店运来a千克苹果,每天卖出b千克,卖了5天,还剩 千克苹果。当a=1000,b=125时,结果是 千克。
答案解析部分
1.720
解:7+2=9,9是3的倍数,这个三位数最大是720。
故答案为:720。
个位上是0,并且各个数位上的数的和是3的倍数,这个数同时是2、3和5的倍数。
2.40
解:10÷(1-)÷(1-)
=10×2×2
=40(元)
故答案为:40。
剩下的钱数占第一次用后剩下钱数的(1-),第一次用后剩下的钱数是总钱数的(1-),由此根据分数除法的意义求出原来的钱数即可。
3.1:2000;3.9
解:16:(320×100)
=16:32000
=1:2000;
78×100×
=7800×
=3.9(厘米)。
故答案为:1:2000;3.9。
先单位换算,这个模型的比例尺=图上距离÷实际距离;图上距离=实际距离×比例尺。
4.210
解:56÷4×15
=14×15
=210(立方厘米)。
故答案为:210。
原来大圆柱的体积=底面积×高,其中,底面积=增加的表面积÷增加底面的个数。
5.;3
解:1÷÷100000
=8000000÷100000
=80(千米)
240×100000×
=24000000×
=3(厘米)。
故答案为:;3。
比例尺=图上距离:实际距离;在这幅地图上应画的长度=实际距离×比例尺,关键是单位换算。
6.3
解:9÷4=2(张)······1(张)
2+1=3(张)。
故答案为:3。
至少有花色相同的牌的张数=人数÷花色的种类数+1张。
7.14
解:24÷(7+5)×7
=24÷12×7
=2×7
=14(小时)。
故答案为:14。
这一天昆明的白昼时间=每天的24小时÷总份数×白昼占的份数。
8.5.6;16.8
解:28×100×
=2800×
=5.6(厘米)
15×100×
=1500×
=3(厘米)
5.6×3=16.8(平方厘米)。
故答案为:5.6;16.8。
图上距离=实际距离×比例尺,关键是先单位换算,图上篮球场的面积=图上的长×图上的宽。
9.1.2
解:0.6×(÷)
=0.6×2
=1.2(小时)。
故答案为:1.2。
行完全程的,需要的时间=0.6小时×全程的 是全程 的倍数。
10.7;8
解:8x=7y
x∶y=7∶8。
故答案为:7;8。
比例的性质:在比例中,两个外项的积等于两个内项的积,这叫作比例的基本性质。
11.340
解:
34000000厘米=340千米
故答案为:340。
求昆明到大理的实际距离是多少千米,根据“图上距离÷比例尺=实际距离”,代入数值,计算即可。
12.﹣6;
解:24÷4=6
如果“D”表示的数是24,则“A”表示的数是-6,如果“B”表示的数是,则“C”表示的数是。
故答案为:-6;。
观察数轴,将D平均分成4份,D÷4=1段表示的数,0的左边是负数,0的右边是正数,A和B到0的距离相同,据此确定A;C等于2个B,因此Bx2=C,据此确定C。
13.11;8
解:A在第11列,第8行,用数对表示出点A的位置是(11,8) 。
故答案为:11;8。
用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数。
14.75;12;32;15
解:=3÷4=0.75=75%;
;
;
===;
所以=75%=9÷12=24:32=。
故答案为:75;12;32;15。
分数化成小数,用分数的分子除以分母,然后把小数的小数点向右移动两位,再加上百分号;
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变;
比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
15.-1;
解:数轴上0的左边每个小格表示0.5,A点表示的数是-1,数轴上0的右边,1的右边每个小格表示,D点表示的数是。
故答案为:-1;。
在数轴上表示数的时候,0的左边表示负数,0的右边表示正数,先观察平均分的份数,再确定每份表示的数,在几后面几格的地方,表示几又几分之几。
16.四千二百零三万三千五百;4203.4
解:42033500读作:四千二百零三万三千五百;
42033500≈4203.4万。
故答案为:四千二百零三万三千五百;4203.4。
亿以上的数的读法:先分级,再从高位读起,读完亿级或万级的数,要加上”亿“字或”万“字,每级末尾不管有几个0都不读,其他数位有一个0或连续几个0,都只读一个零;
用“四舍五入”法求近似数,看需要保留的下一位数,是0~4舍去,是5~9向前一位进一。
17.62.8
解:2米=20分米
(4-1)×2
=3×2
=6(个)
18.84÷6×20
=3.14×20
=62.8(立方分米)。
故答案为:62.8。
原来这根木材的体积=底面积×高;其中,底面积=增加的表面积÷增加底面的个数。
18.;
解:1÷(2 ×2×2 )
=1÷8
=
5÷8= (分米)。
故答案为:; 。
把一根绳子对折三次,是平均分成了8段,每段是全长的分率=1÷平均分的段数,每段的长度=绳子的总长度÷平均分的段数。
19.3:2;
解::=3:2
1÷(+)
=1÷
=(天)。
故答案为:3:2;。
甲乙施工队的比=(1÷甲的工作时间):(1÷乙的工作时间),依据比的基本性质化简比;
甲乙施工队合作施工完成需要的天数=1÷工作效率的和。
20.1.875;1.884
解:近似数是1.88的三位小数最小时,千分位上的数字要向百分位进一,最小是5,这个数是1.875;最大时,千分位上的数要舍去,最大是4,这个数是1.884。
故答案为:1.875;1.884。
用“四舍五入”法求近似数,看需要保留的下一位数,是0~4舍去,是5~9向前一位进一。
21.(1)20;0.3
(2)0.24
解:(1)60-40=20(分)
6÷(80-60)
=6÷20
=0.3(千米/分)
(2)(6×2)÷(40-10+20)
=12÷50
=0.24(千米/分)。
故答案为:(1)20;0.3;(2) 0.24 。
(1)恬恬去时在A处停车休息,恬恬在图书馆借书用的时间=60-40=20分,恬恬骑车返回时的平均速度=恬恬家到图书馆的路程÷返回用的时间;
(2)恬恬骑车往返的平均速度=(恬恬家到图书馆的路程×2) ÷(去时用的时间+返回时用的时间)。
22.(4+2n)
解:2×n+4=(4+2n)(人)。
故答案为:(4+2n)。
n张桌子可以坐的人数=(4+2n)人。
23.20
解:设科技书的进价为x元。售价为27.5×80%=22(元)
(1+10%)x=22
1.1x =22
x=22÷1.1
x=20。
故答案为:20。
本题要求我们求解科技书的进价,已知信息包括定价、折扣率以及利润百分比。解决此问题的关键在于理解“八折售出”和“赚10%”的含义,然后根据这些信息建立等式求解。
24.北偏西30°
解:南和北相对,东和西相对,少年宫在银行的南偏东30°方向上的2000米处,从少年宫到银行需要向北偏西30°方向走2000米。
故答案为:北偏西30°。
两个位置是相对的,分别以它们为观察中心时,看到对方的方向相反,角度和距离相等。
25.95.2%
解:100÷(100+5)
=100÷105
≈95.2%。
故答案为:95.2%。
这批水稻种子的发芽率=发芽的种子粒数÷(发芽的种子粒数+未发芽的种子粒数) 。
26.21
解:2×10+1=21(个)。
故答案为:21。
最坏的情况两种颜色的球各摸出10个,共摸出20个,再摸出一个就保证有3个球不同色。
27.;
解:2×2×2=8(段)
÷8=(米)
3÷8=。
故答案为:;。
把一根绳子对折3次,是平均分成了8段,每段绳子的长度=绳子的总长度÷平均分的段数;3段占全长的分率=3÷平均分的段数。
28.10
解:770÷(7×11)
=770÷77
=10。
故答案为:10。
A和B的最大公因数=A和B公有的质因数相乘;A和B的最小公倍数=A和B公有的质因数×各自独有的质因数。
29.;0
解:×=,所以,,,,,,,……如果按照这样的规律写下去,越来越接近0。
故答案为:;0。
观察已知数字,前一个数字乘即可得到相邻的后一个数字,根据规律确定后面的数字。这组数字越来越小,无穷小后就越接近0。
30.25.12
解:3.14×(2÷2)2×8
=3.14×8
=25.12(dm2)
故答案为:25.12。
锯成5段共锯4次,每锯1次就会增加2个底面积,所以锯成5段会增加8个底面积,因此用木料的底面积乘8就是表面积增加的部分。
31.8
解:1.6÷(1-80%)
=1.6÷20%
=8(元)
故答案为:8。
八折的意思就是现价是原价的80%,比原价省了(1-80%),根据分数除法的意义,用省的钱数除以(1-80%)即可求出原价。
32.﹣6
解:11-5=6(m),蚂蚁向西行了6米,小蚂蚁在-6处。
故答案为:-6。
8分钟后瓢虫距离0点5米远,因为两只小虫相距11米,用11减去5求出小蚂蚁距离0点的长度,根据正负数的意义判断小蚂蚁的位置。向东为正,向西为负。
33.1042000000;10亿
解:十亿四千二百万写作:1042000000,1042000000≈10亿。
故答案为:1042000000;10亿。
写数时从高位到低位按照数位顺序写,有几个计数单位就在相应的数位上写几,没有就写0。根据千万位数字四舍五入省略亿后面的尾数即可。
34.6;36
12的因数有:1、2、3、4、6、12,
18的因数有:1、2、3、6,9、18,
12和18的公因数有:1、2、3、6
12和18的最大公因数是6;
12的倍数有:12、24、36、48、60、72……
18的倍数有:18、36、54、72……
12和18的公倍数有:36、72……
12和18的最小公倍数是:36.
故答案为:6;36.
根据公因数、公倍数的意义,两个数公有的因数叫做这两个数的公因数,其中最大的一个叫做这两个数的最大公因数;两个数公有的倍数叫做这两个数的公倍数,其中最小的一个叫做这两个数的最小公倍数,由此解答.
35.28;(4n+4)
解:4×6+4=28(人)
4×n+4=(4n+4)(人)。
故答案为:28;(4n+4)。
摆n张桌子可以坐的人数=(4n+4)人。
36.2
解:16÷12=1(人)······4(人)
1+1=2(人)。
故答案为:2。
抽屉原理,至少在同一抽屉里相同物体的个数=物体总个数÷抽屉的个数+1。
37.1;12
解:等腰三角形有1条对称轴;
5×2+2=12(厘米)。
故答案为:1;12。
等腰三角形是轴对称图形,有1条对称轴;等腰三角形的周长=腰长×2+底边长。
38.反
解:飞行的速度×时间=飞行的路程(一定),
飞行的速度和时间成反比例。
故答案为:反。
反比例的判断方法:相关联,能变化,积一定。
39.2022070432
解:小亮的学号是: 2022070432 。
故答案为: 2022070432 。
前四位是升入七年级的年份;第五、第六位是年级;第七、第八位是班级;第九、第十位是学号。
40.40;120
解:圆柱体积:80÷(1-)
=80÷
=120(cm3);
圆锥体积:120×=40(cm3)。
故答案为:40;120。
最大的圆锥与原来的圆柱同底同高,圆锥的体积是与它等底等高的圆柱体积的,那么削去部分的体积就是圆柱体积的(1-);已知削去部分的体积,用削去部分的体积除以(1-)接口求出圆柱的体积;再用圆柱的体积乘即可求出圆锥的体积。
41.羊毛的成分
解:“80%羊毛”的含义是:这件羊绒大衣所含的羊毛的成分占这件羊绒大衣总成分的。
故答案为:羊毛的成分。
百分数表示一个是另一个数的百分之几,据此解答。
42.40;960
解:(1000-800)×20%
=200×20%
=40(元);
1000-40=960(元)
故答案为:40;960。
应缴税金额是(1000-800)元,税款=应缴税金额×税率;用稿费减去税款就是税后收入;据此解答。
43.14;(2n+2)
解:6张餐桌:2×6+2=14(人);n张餐桌可坐(2n+2)人。
故答案为:14;(2n+2)。
根据已知图形餐桌的张数与能坐的人数可知,能坐的人数=餐桌张数×2+2,根据规律计算并用含有字母的式子表示这个规律。
44.1:2;1:4
解:长方形ABCD的长和宽分别是4cm和3cm,把它按2:1放大后得到长方形EFGH。长方形ABCD和长方形EFGH的周长之比是1:2,面积之比是1:4。
故答案为:1:2;1:4。
可以分别计算出原来和现在的周长,然后写出周长的比,用同样的方法写出面积的比。也可以根据周长和面积公式直接判断周长和面积的比。
45.(m﹣2n);472
解:这个硬盘还剩(m-2n)G的存储量,当m=512,n=20,还剩余:512-2×20=472(G)。
故答案为:(m-2n);472。
先表示出n部电影需要的内存量,然后用内存总量减去需要的内存量即可表示出还剩的存储量。把m代换成512,n代换成20,求出剩余的存储量即可。
46.29
解:14.5×2=29(cm2)
故答案为:29。
等底等高的平行四边形面积是三角形面积的2倍,三角形ABD和平行四边形ABCD等底等高,所以用三角形ABD的面积乘2即可求出平行四边形ABCD的面积。
47.y<x<z
解:>>,所以y<x<z。
故答案为:y<x<z。
和是相等的,所以只需要比较三个分数的大小即可确定三个字母表示的数的大小。因为和相等,则一个加数大,则另一个加数一定小。
48.4
解:50÷6=8……2,余数是2,说明小数点后第50位上的数是4。
故答案为:4。
“142857”六个数字循环,用50除以6求出商和余数,商是循环节的个数,余数是几,就说明第50位上的数与每个循环节中第几个数字相同。
49.40099000;4010万
解:一个数的千万位上是最小的合数,万位和千位上是最大的一位数,其余各位上都是最小的偶数,这个数写作:40099000,省略万位后面的尾数是4010万。
故答案为:40099000;4010万。
最小的合数是4,最大的一位数是9,从高位到低位写出这个数字;根据千位数字四舍五入省略万位后面的尾数即可。
50.(a﹣5b);375
解:还剩(a-5b)千克苹果;
1000-5×125
=1000-625
=375(千克)
故答案为:(a-5b);375。
剩下的苹果=运来的苹果总量-卖出的,用字母表示各种量写出关系式,把字母表示的具体数量代入关系式中计算出结果。
小升初数学备考真题分类汇编(云南地区专版)
试卷说明:
本试卷试题精选自云南各市,县2024、2023近两年六年级下学期小升初期末真题试卷,难易度均衡,适合云南各市,县的六年级学生小升初择校考、分班考等复习备考使用!
一、填空题
1.(2024·祥云)在0、2、3、6、7这五个数字中选取三个数字组成一个三位数,使它同时是2、3、5的倍数,这个数最大是 。
2.(2024·昭通)小明带了一些钱买文具,先用去所带钱的,又用去剩下钱的,这时还剩下10元。小明原来带了 元。
3.(2024·玉溪) 2022年6月17日我国第三艘航空母舰福建舰成功下水。据悉,它的长是320米,宽是78米,排水量8万余吨。如果按照一定的比例尺制成模型后,长是16厘米,这个模型的比例尺为 ,模型的宽应是 厘米。
4.(2024·曲靖)如下图,把一个高15cm的大圆柱切成3个相同的小圆柱,表面积增加了56cm2,那么原来大圆柱的体积是 cm3。
5.(2024·曲靖) 一幅地图的比例尺是1:8000000,把它改成线段比例尺是 ,已知AB两地的实际距离是240千米,在这幅地图上应画 厘米。
6.(2024·官渡)小明表演扑克牌“魔术”。一副扑克牌,取出大小王,还剩52张牌,9人每人随意抽1张,至少有 张牌是相同的花色。
7.(2024·官渡)一年中,北半球白昼时间最长的一天是“夏至”,黑夜时间最长的一天是“冬至”。2024年的夏至时间是6月21日,昆明这一天的白昼与黑夜的时间比大约是7:5,这一天昆明的白昼时间有 小时。
8.(2024·腾冲)昆明师大附小的一个篮球场的长是28米,宽是15米,把它画在比例尺是1:500的平面图上,篮球场的长在图上的距离是 厘米。图上篮球场的面积是 平方厘米。
9.(2024·腾冲)周末,冬冬一家开车去看望外婆,0.6小时行完全程的,照这样的速度,行完全程的,需要 小时。
10.(2024·五华)如果8x=7y(x,y均不为0),那么x:y= : 。
11.(2024·五华)在一幅比例尺是1:5000000的地图上量得昆明到大理的距离是6.8厘米,昆明到大理的实际距离是 千米。
12.(2024·五华)如图,如果“D”表示的数是24,则“A”表示的数是 ;如果“B”表示的数是,则“C”表示的数是 。
13.(2024·官渡)图中直角梯形②是直角梯形①沿对称轴画出的轴对称图形。根据图中的信息请用数对表示出点A的位置,A( , )。
14.(2024·官渡)= %=9÷ =24: = 。
15.(2024·官渡)数轴上A点表示的数是 ,D点表示的数是 。
16.(2024·官渡)昆明长水国际机场是我国八大区域性枢纽机场之一,2023年旅客吞吐量42033500人次,横线上的数读作 人次,约是 万人次(保留一位小数)。
17.(2024·腾冲)把一段长2米的圆柱形木材锯成4段小圆柱后,表面积总和比原来增加了18.84平方分米,那么原来这根木材的体积是 立方分米。
18.(2024·腾冲)把一根5分米长的绳子对折三次,每段是全长的 ,每段长 分米。
19.(2024·腾冲)今年我市进行污水工程改造,如果甲施工队单独施工需要24天完成,乙施工队单独施工需要36天完成,那么甲乙施工队的工作效率的最简单的整数比是 ,甲乙施工队合作施工,需要 天完成。
20.(2024·腾冲)一个三位小数,精确到百分位约是1.88,这个三位小数最小是 ,最大是 。
21.(2024·曲靖)恬恬骑车从家去相距6千米的图书馆借书,根据如图所示的统计图解决问题。
(1)恬恬去时在A处停车休息,恬恬在图书馆借书用了 分钟,恬恬骑车返回时的平均速度是 千米/分。
(2)恬恬骑车往返的平均速度是 千米/分。(不含中途休息和借书时间)
22.(2024·曲靖) 一张长方形桌子可坐6人,按图中的方式将桌子拼在一起。n张桌子可坐 人。
23.(2024·曲靖) 一本定价27.5元的科技书,八折售出仍可以赚10%,这本科技书进价是 元。
24.(2024·曲靖)少年宫在银行的南偏东30°方向上的2000米处,从少年宫到银行需要向 方向走2000米。
25.(2024·曲靖)做一批水稻种子发芽实验,发芽的有100粒,未发芽的有5粒。这批水稻种子的发芽率是 。(百分号前保留一位小数)
26.(2024·曲靖) 一个袋子里有同样大小的红、白、蓝三种球各10个,至少摸出 个球才能保证有3个球不同色。
27.(2024·曲靖)把一根米长的绳子对折三次,沿折痕剪开,每段绳子长 米,3段绳子占全长的 。
28.(2024·曲靖)a=2×m×7,b=2×11×m,a、b两数的最小公倍数770,a、b两数的最大公因数是 。
29.(2024·昭通)找规律填数:
,,,,,, ……如果按照这样的规律写下去,越来越接近 。
30.(2024·昭通) 一根圆柱形木料,底面直径是2dm,长2.5m,沿横截面平均锯成5段圆柱形木料,表面积增加了 dm2。
31.(2024·昭通)“六一”节,某书店的图书一律打八折销售。小军买了一本《趣味数学》,省了1.6元。这本书的原价是 元。
32.(2024·昭通) 一只蚂蚁和一只七星瓢虫同时从“0”出发,背向而行(如图,每小格代表1m)。行了8分钟,这时两只小虫相距11m,七星瓢虫在“5”处,小蚂蚁在 处。
33.(2024·昭通) 2023年云南旅游持续恢复回暖。云南省《政府工作报告》中指出,2023年,全省接待游客十亿四千二百万人次,旅游总收入达1.44万亿元。报告还指出,2024年云南将聚焦文化和旅游强省目标,让“有一种叫云南的生活”更加深入人心,旅游总收入力争突破1.5万亿元。横线上这个数写作 人次,省略亿位后面的尾数是 人次。
34.(2024·广州)12和18的最大公因数是 ,最小公倍数是 .
35.(2024·玉溪) 五一期间新平举办了“腌菜长街宴”,吸引了不少游客。长街宴就是将若干张桌子拼成长长的宴席(如图)。如果每张桌子每边坐2人,那么摆一张桌子可以坐8人,摆2张桌子可以坐12人,摆3张桌子可以坐16人,摆6张桌子可以坐 人,摆n张桌子可以坐 人。
36.(2024·玉溪) 六⑵班综合实践小队有16个孩子,他们至少有 个人的属相相同。
37.(2024·玉溪) 一个三角形三个内角度数比是4:4:1,这个三角形有 条对称轴;如果它两边的长分别是2厘米和5厘米,则它的周长为 厘米。
38.(2023·红河)一架飞机从昆明飞往北京,飞行的速度和时间成 比例。
39.(2023·红河)小东2022年升入七年级(4)班,他的座位号是16,学号是2022070416。同班的小亮座位号是32 。
40.(2023·德宏)把一个圆柱削成一个最大的圆锥,削去的体积是80cm3,则圆锥的体积是 cm3,圆柱的体积是 cm3。
41.(2023·德宏) 一件羊绒大衣的标签上写着:“80%羊毛,20%羊绒”。“80%羊毛”的含义是:这件羊绒大衣所含的 占这件羊绒大衣总成分的。
42.(2023·德宏)张叔叔得到一笔1000元的稿费。其中800元是免税的,其余部分按20%的税率缴税,张叔叔应缴税 元,税后收入是 元。
43.(2023·麒麟)如图,1张餐桌可坐4人,2张餐桌拼在一起可坐6人,3张餐桌拼在一起可坐8人。按照这样拼桌,6张餐桌可坐 人,n张餐桌可坐 人。
44.(2023·麒麟)长方形ABCD的长和宽分别是4cm和3cm,把它按2:1放大后得到长方形EFGH。长方形ABCD和长方形EFGH的周长之比是 ,面积之比是 。
45.(2023·麒麟)一个移动硬盘的存储量是mG,存储一部电影约需2G的内存量,存了n部电影,这个硬盘还剩 G的存储量;当m=512,n=20,还剩余 G的存储量。
46.(2023·麒麟)图中三角形ABD的面积是14.5cm2,平行四边形ABCE的面积是 cm2。
47.(2023·麒麟)已知 那么把x,y,z按从小到大的顺序排列是: 。
48.(2023·麒麟)已知 ,小数点后第50位上的数是 。
49.(2023·麒麟)一个数的千万位上是最小的合数,万位和千位上是最大的一位数,其余各位上都是最小的偶数,这个数写作: ,省略万位后面的尾数是 。
50.(2022·麒麟)水果店运来a千克苹果,每天卖出b千克,卖了5天,还剩 千克苹果。当a=1000,b=125时,结果是 千克。
答案解析部分
1.720
解:7+2=9,9是3的倍数,这个三位数最大是720。
故答案为:720。
个位上是0,并且各个数位上的数的和是3的倍数,这个数同时是2、3和5的倍数。
2.40
解:10÷(1-)÷(1-)
=10×2×2
=40(元)
故答案为:40。
剩下的钱数占第一次用后剩下钱数的(1-),第一次用后剩下的钱数是总钱数的(1-),由此根据分数除法的意义求出原来的钱数即可。
3.1:2000;3.9
解:16:(320×100)
=16:32000
=1:2000;
78×100×
=7800×
=3.9(厘米)。
故答案为:1:2000;3.9。
先单位换算,这个模型的比例尺=图上距离÷实际距离;图上距离=实际距离×比例尺。
4.210
解:56÷4×15
=14×15
=210(立方厘米)。
故答案为:210。
原来大圆柱的体积=底面积×高,其中,底面积=增加的表面积÷增加底面的个数。
5.;3
解:1÷÷100000
=8000000÷100000
=80(千米)
240×100000×
=24000000×
=3(厘米)。
故答案为:;3。
比例尺=图上距离:实际距离;在这幅地图上应画的长度=实际距离×比例尺,关键是单位换算。
6.3
解:9÷4=2(张)······1(张)
2+1=3(张)。
故答案为:3。
至少有花色相同的牌的张数=人数÷花色的种类数+1张。
7.14
解:24÷(7+5)×7
=24÷12×7
=2×7
=14(小时)。
故答案为:14。
这一天昆明的白昼时间=每天的24小时÷总份数×白昼占的份数。
8.5.6;16.8
解:28×100×
=2800×
=5.6(厘米)
15×100×
=1500×
=3(厘米)
5.6×3=16.8(平方厘米)。
故答案为:5.6;16.8。
图上距离=实际距离×比例尺,关键是先单位换算,图上篮球场的面积=图上的长×图上的宽。
9.1.2
解:0.6×(÷)
=0.6×2
=1.2(小时)。
故答案为:1.2。
行完全程的,需要的时间=0.6小时×全程的 是全程 的倍数。
10.7;8
解:8x=7y
x∶y=7∶8。
故答案为:7;8。
比例的性质:在比例中,两个外项的积等于两个内项的积,这叫作比例的基本性质。
11.340
解:
34000000厘米=340千米
故答案为:340。
求昆明到大理的实际距离是多少千米,根据“图上距离÷比例尺=实际距离”,代入数值,计算即可。
12.﹣6;
解:24÷4=6
如果“D”表示的数是24,则“A”表示的数是-6,如果“B”表示的数是,则“C”表示的数是。
故答案为:-6;。
观察数轴,将D平均分成4份,D÷4=1段表示的数,0的左边是负数,0的右边是正数,A和B到0的距离相同,据此确定A;C等于2个B,因此Bx2=C,据此确定C。
13.11;8
解:A在第11列,第8行,用数对表示出点A的位置是(11,8) 。
故答案为:11;8。
用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数。
14.75;12;32;15
解:=3÷4=0.75=75%;
;
;
===;
所以=75%=9÷12=24:32=。
故答案为:75;12;32;15。
分数化成小数,用分数的分子除以分母,然后把小数的小数点向右移动两位,再加上百分号;
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变;
比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
15.-1;
解:数轴上0的左边每个小格表示0.5,A点表示的数是-1,数轴上0的右边,1的右边每个小格表示,D点表示的数是。
故答案为:-1;。
在数轴上表示数的时候,0的左边表示负数,0的右边表示正数,先观察平均分的份数,再确定每份表示的数,在几后面几格的地方,表示几又几分之几。
16.四千二百零三万三千五百;4203.4
解:42033500读作:四千二百零三万三千五百;
42033500≈4203.4万。
故答案为:四千二百零三万三千五百;4203.4。
亿以上的数的读法:先分级,再从高位读起,读完亿级或万级的数,要加上”亿“字或”万“字,每级末尾不管有几个0都不读,其他数位有一个0或连续几个0,都只读一个零;
用“四舍五入”法求近似数,看需要保留的下一位数,是0~4舍去,是5~9向前一位进一。
17.62.8
解:2米=20分米
(4-1)×2
=3×2
=6(个)
18.84÷6×20
=3.14×20
=62.8(立方分米)。
故答案为:62.8。
原来这根木材的体积=底面积×高;其中,底面积=增加的表面积÷增加底面的个数。
18.;
解:1÷(2 ×2×2 )
=1÷8
=
5÷8= (分米)。
故答案为:; 。
把一根绳子对折三次,是平均分成了8段,每段是全长的分率=1÷平均分的段数,每段的长度=绳子的总长度÷平均分的段数。
19.3:2;
解::=3:2
1÷(+)
=1÷
=(天)。
故答案为:3:2;。
甲乙施工队的比=(1÷甲的工作时间):(1÷乙的工作时间),依据比的基本性质化简比;
甲乙施工队合作施工完成需要的天数=1÷工作效率的和。
20.1.875;1.884
解:近似数是1.88的三位小数最小时,千分位上的数字要向百分位进一,最小是5,这个数是1.875;最大时,千分位上的数要舍去,最大是4,这个数是1.884。
故答案为:1.875;1.884。
用“四舍五入”法求近似数,看需要保留的下一位数,是0~4舍去,是5~9向前一位进一。
21.(1)20;0.3
(2)0.24
解:(1)60-40=20(分)
6÷(80-60)
=6÷20
=0.3(千米/分)
(2)(6×2)÷(40-10+20)
=12÷50
=0.24(千米/分)。
故答案为:(1)20;0.3;(2) 0.24 。
(1)恬恬去时在A处停车休息,恬恬在图书馆借书用的时间=60-40=20分,恬恬骑车返回时的平均速度=恬恬家到图书馆的路程÷返回用的时间;
(2)恬恬骑车往返的平均速度=(恬恬家到图书馆的路程×2) ÷(去时用的时间+返回时用的时间)。
22.(4+2n)
解:2×n+4=(4+2n)(人)。
故答案为:(4+2n)。
n张桌子可以坐的人数=(4+2n)人。
23.20
解:设科技书的进价为x元。售价为27.5×80%=22(元)
(1+10%)x=22
1.1x =22
x=22÷1.1
x=20。
故答案为:20。
本题要求我们求解科技书的进价,已知信息包括定价、折扣率以及利润百分比。解决此问题的关键在于理解“八折售出”和“赚10%”的含义,然后根据这些信息建立等式求解。
24.北偏西30°
解:南和北相对,东和西相对,少年宫在银行的南偏东30°方向上的2000米处,从少年宫到银行需要向北偏西30°方向走2000米。
故答案为:北偏西30°。
两个位置是相对的,分别以它们为观察中心时,看到对方的方向相反,角度和距离相等。
25.95.2%
解:100÷(100+5)
=100÷105
≈95.2%。
故答案为:95.2%。
这批水稻种子的发芽率=发芽的种子粒数÷(发芽的种子粒数+未发芽的种子粒数) 。
26.21
解:2×10+1=21(个)。
故答案为:21。
最坏的情况两种颜色的球各摸出10个,共摸出20个,再摸出一个就保证有3个球不同色。
27.;
解:2×2×2=8(段)
÷8=(米)
3÷8=。
故答案为:;。
把一根绳子对折3次,是平均分成了8段,每段绳子的长度=绳子的总长度÷平均分的段数;3段占全长的分率=3÷平均分的段数。
28.10
解:770÷(7×11)
=770÷77
=10。
故答案为:10。
A和B的最大公因数=A和B公有的质因数相乘;A和B的最小公倍数=A和B公有的质因数×各自独有的质因数。
29.;0
解:×=,所以,,,,,,,……如果按照这样的规律写下去,越来越接近0。
故答案为:;0。
观察已知数字,前一个数字乘即可得到相邻的后一个数字,根据规律确定后面的数字。这组数字越来越小,无穷小后就越接近0。
30.25.12
解:3.14×(2÷2)2×8
=3.14×8
=25.12(dm2)
故答案为:25.12。
锯成5段共锯4次,每锯1次就会增加2个底面积,所以锯成5段会增加8个底面积,因此用木料的底面积乘8就是表面积增加的部分。
31.8
解:1.6÷(1-80%)
=1.6÷20%
=8(元)
故答案为:8。
八折的意思就是现价是原价的80%,比原价省了(1-80%),根据分数除法的意义,用省的钱数除以(1-80%)即可求出原价。
32.﹣6
解:11-5=6(m),蚂蚁向西行了6米,小蚂蚁在-6处。
故答案为:-6。
8分钟后瓢虫距离0点5米远,因为两只小虫相距11米,用11减去5求出小蚂蚁距离0点的长度,根据正负数的意义判断小蚂蚁的位置。向东为正,向西为负。
33.1042000000;10亿
解:十亿四千二百万写作:1042000000,1042000000≈10亿。
故答案为:1042000000;10亿。
写数时从高位到低位按照数位顺序写,有几个计数单位就在相应的数位上写几,没有就写0。根据千万位数字四舍五入省略亿后面的尾数即可。
34.6;36
12的因数有:1、2、3、4、6、12,
18的因数有:1、2、3、6,9、18,
12和18的公因数有:1、2、3、6
12和18的最大公因数是6;
12的倍数有:12、24、36、48、60、72……
18的倍数有:18、36、54、72……
12和18的公倍数有:36、72……
12和18的最小公倍数是:36.
故答案为:6;36.
根据公因数、公倍数的意义,两个数公有的因数叫做这两个数的公因数,其中最大的一个叫做这两个数的最大公因数;两个数公有的倍数叫做这两个数的公倍数,其中最小的一个叫做这两个数的最小公倍数,由此解答.
35.28;(4n+4)
解:4×6+4=28(人)
4×n+4=(4n+4)(人)。
故答案为:28;(4n+4)。
摆n张桌子可以坐的人数=(4n+4)人。
36.2
解:16÷12=1(人)······4(人)
1+1=2(人)。
故答案为:2。
抽屉原理,至少在同一抽屉里相同物体的个数=物体总个数÷抽屉的个数+1。
37.1;12
解:等腰三角形有1条对称轴;
5×2+2=12(厘米)。
故答案为:1;12。
等腰三角形是轴对称图形,有1条对称轴;等腰三角形的周长=腰长×2+底边长。
38.反
解:飞行的速度×时间=飞行的路程(一定),
飞行的速度和时间成反比例。
故答案为:反。
反比例的判断方法:相关联,能变化,积一定。
39.2022070432
解:小亮的学号是: 2022070432 。
故答案为: 2022070432 。
前四位是升入七年级的年份;第五、第六位是年级;第七、第八位是班级;第九、第十位是学号。
40.40;120
解:圆柱体积:80÷(1-)
=80÷
=120(cm3);
圆锥体积:120×=40(cm3)。
故答案为:40;120。
最大的圆锥与原来的圆柱同底同高,圆锥的体积是与它等底等高的圆柱体积的,那么削去部分的体积就是圆柱体积的(1-);已知削去部分的体积,用削去部分的体积除以(1-)接口求出圆柱的体积;再用圆柱的体积乘即可求出圆锥的体积。
41.羊毛的成分
解:“80%羊毛”的含义是:这件羊绒大衣所含的羊毛的成分占这件羊绒大衣总成分的。
故答案为:羊毛的成分。
百分数表示一个是另一个数的百分之几,据此解答。
42.40;960
解:(1000-800)×20%
=200×20%
=40(元);
1000-40=960(元)
故答案为:40;960。
应缴税金额是(1000-800)元,税款=应缴税金额×税率;用稿费减去税款就是税后收入;据此解答。
43.14;(2n+2)
解:6张餐桌:2×6+2=14(人);n张餐桌可坐(2n+2)人。
故答案为:14;(2n+2)。
根据已知图形餐桌的张数与能坐的人数可知,能坐的人数=餐桌张数×2+2,根据规律计算并用含有字母的式子表示这个规律。
44.1:2;1:4
解:长方形ABCD的长和宽分别是4cm和3cm,把它按2:1放大后得到长方形EFGH。长方形ABCD和长方形EFGH的周长之比是1:2,面积之比是1:4。
故答案为:1:2;1:4。
可以分别计算出原来和现在的周长,然后写出周长的比,用同样的方法写出面积的比。也可以根据周长和面积公式直接判断周长和面积的比。
45.(m﹣2n);472
解:这个硬盘还剩(m-2n)G的存储量,当m=512,n=20,还剩余:512-2×20=472(G)。
故答案为:(m-2n);472。
先表示出n部电影需要的内存量,然后用内存总量减去需要的内存量即可表示出还剩的存储量。把m代换成512,n代换成20,求出剩余的存储量即可。
46.29
解:14.5×2=29(cm2)
故答案为:29。
等底等高的平行四边形面积是三角形面积的2倍,三角形ABD和平行四边形ABCD等底等高,所以用三角形ABD的面积乘2即可求出平行四边形ABCD的面积。
47.y<x<z
解:>>,所以y<x<z。
故答案为:y<x<z。
和是相等的,所以只需要比较三个分数的大小即可确定三个字母表示的数的大小。因为和相等,则一个加数大,则另一个加数一定小。
48.4
解:50÷6=8……2,余数是2,说明小数点后第50位上的数是4。
故答案为:4。
“142857”六个数字循环,用50除以6求出商和余数,商是循环节的个数,余数是几,就说明第50位上的数与每个循环节中第几个数字相同。
49.40099000;4010万
解:一个数的千万位上是最小的合数,万位和千位上是最大的一位数,其余各位上都是最小的偶数,这个数写作:40099000,省略万位后面的尾数是4010万。
故答案为:40099000;4010万。
最小的合数是4,最大的一位数是9,从高位到低位写出这个数字;根据千位数字四舍五入省略万位后面的尾数即可。
50.(a﹣5b);375
解:还剩(a-5b)千克苹果;
1000-5×125
=1000-625
=375(千克)
故答案为:(a-5b);375。
剩下的苹果=运来的苹果总量-卖出的,用字母表示各种量写出关系式,把字母表示的具体数量代入关系式中计算出结果。
同课章节目录
