2025年普通高等学校招生全国统一考试模拟试题 数学(一)PPT课件
文档属性
| 名称 | 2025年普通高等学校招生全国统一考试模拟试题 数学(一)PPT课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 09:39:42 | ||
图片预览










文档简介
(共48张PPT)
2025年普通高等学校招生全国统一考试模拟试题
数学(一)
本试卷共4页,19题。全卷满分150分。考试用时120分钟。
注意事项:
1.答题前,先将自己的姓名、考号等填写在答题卡上,并将准考证号条形码粘贴在
答题卡上的指定位置。
2.选择题的作答:选出每小题答案后,用
黑。写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.填空题和解答题的作答:用签字笔直接写在答题卡上对应的答题区域内。写在试
题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,
只有一项是符合题目要求的。
1.若,则 在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
[解析] 由题得,所以 ,它在复平面内对应
的点为 ,位于第二象限.故选B.
√
2.设集合,,若 ,则( )
A. B. C. D.
[解析] 由已知得,若 ,则 .故选C.
√
3.若函数在上单调递增,则 的取值范围为( )
A. B. C. D.
[解析] 函数在 上单调递增,由复合函数的单调性可知,函数
在上单调递增,故 .故选D.
√
4.在中,点在边上,,则 的最大值为 ( )
A. B. C. D.1
[解析] 由点在边上,得,又,,所以 ,当且仅当
时等号成立,所以 .故选A.
√
5.某单位举办了一次学习强国知识竞赛(满分:100分),参加竞赛的职工共有30人,其
中男、女职工人数相等,他们竞赛得分的总平均值是90,男职工得分的平均值和方差分
别是88和2,女职工得分的平均值和方差分别为92和 ,则该单位所有参赛职工得分的
方差为( )
A.5.4 B.5.6 C.5.7 D.5.9
[解析] 设所有职工得分的平均值和方差分别是和 ,其中男职工得分的平均值和方差
分别是和,女职工得分的平均值和方差分别是和 ,由方
差公式可得 .故选C.
√
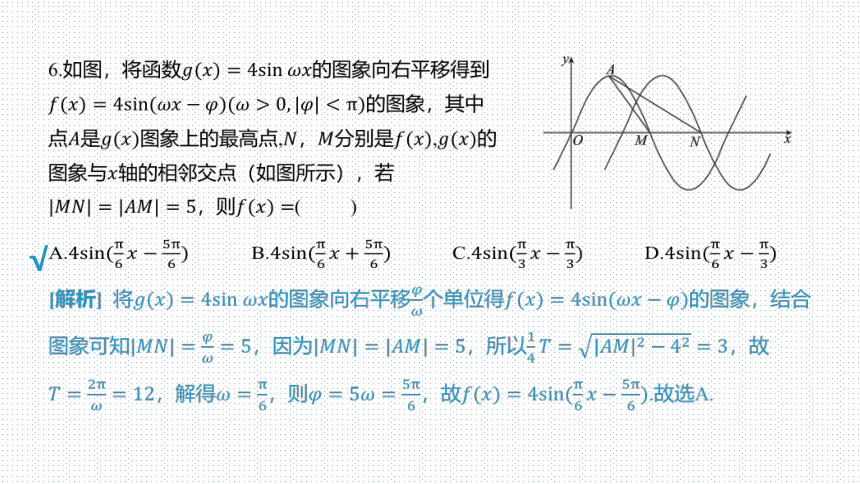
6.如图,将函数 的图象向右平移得到
的图象,其中
点是图象上的最高点,,分别是, 的
图象与 轴的相邻交点(如图所示),若
,则 ( )
A. B. C. D.
[解析] 将的图象向右平移个单位得 的图象,结合
图象可知,因为,所以 ,故
,解得,则,故 .故选A.
√
7.已知正四棱锥的各棱长均相等,球 是该四棱锥的内切球,若该球的表面积
为 ,则该正四棱锥的高为( )
A. B. C. D.
[解析] 设,底面的中心为,连接,则 ,设
球的半径为,由球的表面积为 ,得 ,由等体积法得
,即 ,解得
,故该四棱锥的高为 .故选B.
√
8.已知函数有且仅有3个零点,则 的取值范围为( )
A. B. C. D.
√
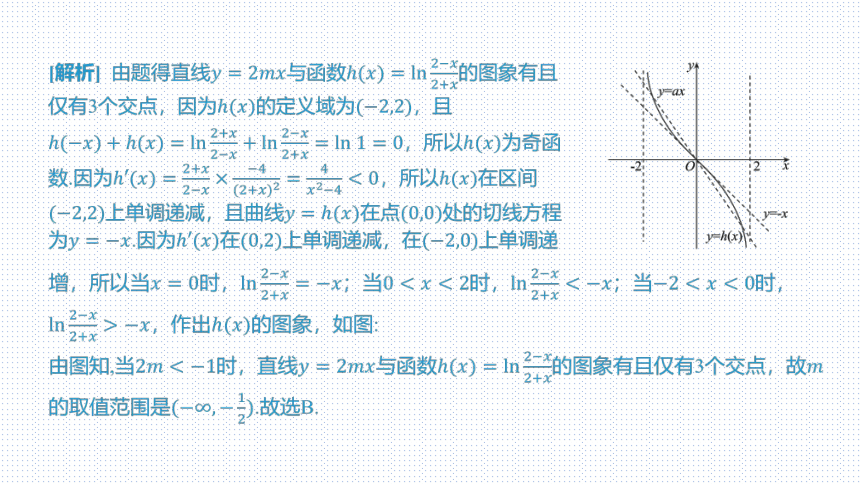
[解析] 由题得直线与函数 的图象有且
仅有3个交点,因为的定义域为 ,且
,所以 为奇函
数.因为,所以 在区间
上单调递减,且曲线在点 处的切线方程
为.因为在上单调递减,在 上单调递
增,所以当时,;当时,;当 时,
,作出 的图象,如图:
由图知,当时,直线与函数的图象有且仅有3个交点,故
的取值范围是 .故选B.
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多
项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.已知 的展开式中各项系数的和为64,则( )
A.
B.展开式中常数项为540
C.展开式中含 项的系数为135
D.展开式中各项系数的绝对值的和为4 096
√
√
√
[解析] 对于A,令,得,则,故A正确;对于B, 的展开式的
通项公式为,当时, ,所以
的展开式中常数项为,故B错误;对于C,当 时,
,所以的展开式中含项的系数为 ,故C正确;对于D,
的展开式系数的绝对值的和可看作是的展开式中系数的和,令 ,
的展开式中系数的和为,故D正确.故选 .
10.椭圆具有对称美,受到设计师的青睐.现有一工艺品,其图案的基本图形由正方形和
内嵌其中的“斜椭圆”组成(如图).在平面直角坐标系 中,将标准方程表示的椭圆绕
着对称中心旋转一定角度,即得“斜椭圆”.已知“斜椭圆”的方程为 ,其
左、右焦点分别为,,设在 上,则( )
A.的长轴长为
B. 的焦距为4
C.若 ,则 的面积为2
D.
√
√
√
[解析] 设的长轴长为,短轴长为,焦距为.由方程可知,关于直线与
对称,且关于原点对称,故的中心为,顶点为与直线, 的交点.由
,得,所以的其中2个顶点为, ,由
,得,所以的另外2个顶点为和 ,易求得
,,所以,,,故长轴长为 ,A错误;
焦距,B正确;将该椭圆还原成焦点在轴上的标准椭圆,其方程为 ,
设该椭圆焦点分别为,,点在该椭圆上,则 ,又由椭圆
定义可知, ,即
,解得 ,又
,所以的面积为,故C正确; ,
由椭圆的性质可知,当点为长轴的端点时,取得最大值,当点 为短轴的端
点时,取得最小值,故D正确.故选 .
11.已知函数对任意实数,都有 ,且
,则( )
A. B.
C.是一个周期为4的周期函数 D.
√
√
√
[解析] 由 ,得
,令 ,得
,则,A正确;令 ,得
,因此 ,则
,于是得,即 ,
,即函数 是周期为8的周期函数,C错误;
,B正确;又, ,
,, ,即
,因此
,D正确.故选 .
三、填空题:本题共3小题,每小题5分,共15分。
12.已知在等比数列中,, ,则数
列 的公比为___.
2
[解析] 设公比为 ,则
,
解得 .
13.汤圆是汉族传统小吃的代表之一,同时也是中国的传统节日元宵节最具有特色的食
物,表达了人民对幸福生活的一种向往和期盼.在广东省流行四式汤圆,这四式汤圆指
的是四种不同的馅:绿豆、红豆、糖冬瓜、芋头,小王在今年元宵节时,盛了一碗(10个)
汤圆,其中绿豆馅、红豆馅的汤圆各4个,糖冬瓜馅、芋头馅的各1个,则小王在碗里随
机取的4个汤圆中,吃到1个芋头馅的前提下,4个汤圆恰有4种馅的概率为___.
[解析] 记事件为“小王随机取的4个汤圆中有1个芋头馅的汤圆”,事件 为“小王随机取
的4个汤圆中恰有4种馅”,所以, ,所以
.
14.已知抛物线的焦点为,直线经过点交于,两点(点 在第一象限),
且,两点在的准线上的投影分别为,,准线与轴的交点为,分别记 与
的面积为,,若,则直线 的斜率为____.
[解析] 由题得 ,所以
,所以.如图,过点作 于
点,所以,设,则 ,则
,所以
,所以 ,所以直线 的斜率
.
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(本小题满分13分)
激光一体机是一种功能强大的办公设备,与传统的激光打印机相比,激光一体机还
集成了复印、扫描等多种功能,因此比传统的激光打印机更实用,从而近几年在全国各
地逐渐热销起来.下表为市统计的近5年该市激光一体机的销量,其中为年份代号,
(单位:万台)代表年销量.
年份 2021年 2021年 2022年 2023年 2024年
年份代号 1 2 3 4 5
年销量 万台 0.5 0.9 1 1.2 1.4
(1)经过分析,与线性相关,试求关于 的经验回归方程;
解: ,
,
(1分)
则 ,(4分)
,(5分)
所以关于的经验回归方程为 .(6分)
(2)利用(1)中所求方程,预测2025年该市激光一体机的销量;
解:2025年对应的年份代码 为6,
当时, (万台),
故可预测2025年该市激光一体机的销量约为1.63万台.(9分)
(3)某中学准备选购某型号的激光一体机供各办公室使用,下表是以往这种型号的激
光一体机的使用年限(整年)统计表:
使用年限 1年 2年 3年 4年 5年
该型号激光一体机(单位:台) 5 15 20 10 50
激光一体机使用年限越长,办公费用越低.以使用年限的频率估计概率,求该型号激光
一体机使用年限的分布列及数学期望 .
参考公式:, .
参考数据:, .
解:以频率估计概率,该型号激光一体机的使用年限 的分布列为:
1 2 3 4 5
0.05 0.15 0.2 0.1 0.5
(11分)
.(13分)
16.(本小题满分15分)
记数列的前项和为,已知, .
(1)求数列 的通项公式;
解:因为 ,
所以 ,
当时, ,
两式相减得 ,
整理得 ,
即 ,(4分)
又 ,
所以数列是以9为首项, 为公差的等差数列.(5分)
所以 .(6分)
(2)若,求数列的前项和 ;
解:由(1)得 ,(7分)
由,解得 .
所以当时, .(9分)
当时, .(10分)
所以 (11分)
(3)记,求数列的前项和 .
解:
,(13分)
所以
.(15分)
17.(本小题满分15分)
已知函数,且在 处取得极值.
(1)求的值及 的单调区间;
解:由题得 ,
由,解得 ,(2分)
此时, ,
令,得 ,
令,得 ,
故0是函数的极值点,
故 符合要求,(4分)
函数的单调递增区间是,单调递减区间是 .(5分)
(2)若存在,使得,求实数 的取值范围.
解:由 ,
可得 ,
则 ,(7分)
令 ,
则 ,
令 ,
则 ,(10分)
故当时,, 单调递增;
当时,, 单调递减,
而,,且时, ,
故当时, ,
当时, ,(12分)
故在上单调递减,在 上单调递增,
故 ,
因此,解得 ,
所以的取值范围为 .(15分)
18.(本小题满分17分)
已知双曲线的左、右焦点分别为,,,且点
到的渐近线的距离为,,为上在 轴上方的两点.
(1)求 的方程;
解:由题意知,得 .(1分)
因为点到直线的距离为 ,
所以 ,
又因为 ,
所以, ,(2分)
所以的方程为 .(3分)
(2)记的左顶点为,若直线与轴平行,证明:直线, 的斜率之积为定值;
解:由(1)知 ,
设,则, ,
所以 ,(5分)
因为 ,
所以 ,
所以直线,的斜率之积为定值 .(6分)
(3)若,求四边形 面积的取值范围.
解:根据对称性,设点在的左支上,点在 的右支上.
如图所示,延长交于点,延长交于点 ,
因为 ,
所以四边形为平行四边形,且面积为四边形 面积
的2倍,(7分)
易知直线 斜率不为0.
设,,直线, ,
由,消去 可得
,
恒成立,
所以, ,(9分)
所以,且
,(11分)
因为,所以 .(12分)
因为直线与间的距离为 ,(13分)
所以 ,(15分)
令, ,
所以 ,
因为在上单调递减,且 ,
所以在 上单调递增,
当,即时,四边形 的面积取得最小值,最小值为48,
所以四边形面积的取值范围为 .(17分)
19.(本小题满分17分)
如图,四边形是边长为2的正方形,点,分别在线段, 上运动,且
.将沿折起,使得点到达点的位置,此时平面 平面 .
(1)当为 的中点时,
(ⅰ)证明: ;
解:当为的中点时,为的中点,此时, ,
.
如图,取的中点,连接, ,
则, ,
又,, 平面 ,
所以 平面 ,
又 平面 ,
所以 .(4分)
(ⅱ)求点到平面 的距离.
解:设点到平面的距离为 ,
,
因为平面 平面,平面 平面, ,
所以 平面 ,
因为 平面 ,
所以 ,
则 ,
所以 ,
所以 ,
.(7分)
由 ,
得 ,
所以 ,
即点到平面的距离为 .(8分)
(2)证明:存在点,使得二面角的平面角为 .
[答案] 如图,以点为坐标原点,, 所
在直线分别为, 轴建立如下图所示的空间
直角坐标系,
过点在平面内作,连接 ,
由已知可得, ,
, ,
故 ,
则 ,
即,且 ,
因为平面 平面,平面
平面, 平面 ,
所以 平面 ,
设, ,
则 , ,
因为 ,
则 ,
,
易得 ,
则点,, ,
, ,
设平面的一个法向量为 ,则
,(12分)
令 ,可得 ,
易知平面的一个法向量为 ,
,
因为 ,
令,
,
可得
,
即 ,(14分)
所以
,
令 ,
令
,
易知函数在 上连续,
因为, ,
由零点存在性定理可知,存在,使得 ,
因此,存在点,使得二面角的的平面角为 .(17分)
2025年普通高等学校招生全国统一考试模拟试题
数学(一)
本试卷共4页,19题。全卷满分150分。考试用时120分钟。
注意事项:
1.答题前,先将自己的姓名、考号等填写在答题卡上,并将准考证号条形码粘贴在
答题卡上的指定位置。
2.选择题的作答:选出每小题答案后,用
黑。写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.填空题和解答题的作答:用签字笔直接写在答题卡上对应的答题区域内。写在试
题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,
只有一项是符合题目要求的。
1.若,则 在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
[解析] 由题得,所以 ,它在复平面内对应
的点为 ,位于第二象限.故选B.
√
2.设集合,,若 ,则( )
A. B. C. D.
[解析] 由已知得,若 ,则 .故选C.
√
3.若函数在上单调递增,则 的取值范围为( )
A. B. C. D.
[解析] 函数在 上单调递增,由复合函数的单调性可知,函数
在上单调递增,故 .故选D.
√
4.在中,点在边上,,则 的最大值为 ( )
A. B. C. D.1
[解析] 由点在边上,得,又,,所以 ,当且仅当
时等号成立,所以 .故选A.
√
5.某单位举办了一次学习强国知识竞赛(满分:100分),参加竞赛的职工共有30人,其
中男、女职工人数相等,他们竞赛得分的总平均值是90,男职工得分的平均值和方差分
别是88和2,女职工得分的平均值和方差分别为92和 ,则该单位所有参赛职工得分的
方差为( )
A.5.4 B.5.6 C.5.7 D.5.9
[解析] 设所有职工得分的平均值和方差分别是和 ,其中男职工得分的平均值和方差
分别是和,女职工得分的平均值和方差分别是和 ,由方
差公式可得 .故选C.
√
6.如图,将函数 的图象向右平移得到
的图象,其中
点是图象上的最高点,,分别是, 的
图象与 轴的相邻交点(如图所示),若
,则 ( )
A. B. C. D.
[解析] 将的图象向右平移个单位得 的图象,结合
图象可知,因为,所以 ,故
,解得,则,故 .故选A.
√
7.已知正四棱锥的各棱长均相等,球 是该四棱锥的内切球,若该球的表面积
为 ,则该正四棱锥的高为( )
A. B. C. D.
[解析] 设,底面的中心为,连接,则 ,设
球的半径为,由球的表面积为 ,得 ,由等体积法得
,即 ,解得
,故该四棱锥的高为 .故选B.
√
8.已知函数有且仅有3个零点,则 的取值范围为( )
A. B. C. D.
√
[解析] 由题得直线与函数 的图象有且
仅有3个交点,因为的定义域为 ,且
,所以 为奇函
数.因为,所以 在区间
上单调递减,且曲线在点 处的切线方程
为.因为在上单调递减,在 上单调递
增,所以当时,;当时,;当 时,
,作出 的图象,如图:
由图知,当时,直线与函数的图象有且仅有3个交点,故
的取值范围是 .故选B.
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多
项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.已知 的展开式中各项系数的和为64,则( )
A.
B.展开式中常数项为540
C.展开式中含 项的系数为135
D.展开式中各项系数的绝对值的和为4 096
√
√
√
[解析] 对于A,令,得,则,故A正确;对于B, 的展开式的
通项公式为,当时, ,所以
的展开式中常数项为,故B错误;对于C,当 时,
,所以的展开式中含项的系数为 ,故C正确;对于D,
的展开式系数的绝对值的和可看作是的展开式中系数的和,令 ,
的展开式中系数的和为,故D正确.故选 .
10.椭圆具有对称美,受到设计师的青睐.现有一工艺品,其图案的基本图形由正方形和
内嵌其中的“斜椭圆”组成(如图).在平面直角坐标系 中,将标准方程表示的椭圆绕
着对称中心旋转一定角度,即得“斜椭圆”.已知“斜椭圆”的方程为 ,其
左、右焦点分别为,,设在 上,则( )
A.的长轴长为
B. 的焦距为4
C.若 ,则 的面积为2
D.
√
√
√
[解析] 设的长轴长为,短轴长为,焦距为.由方程可知,关于直线与
对称,且关于原点对称,故的中心为,顶点为与直线, 的交点.由
,得,所以的其中2个顶点为, ,由
,得,所以的另外2个顶点为和 ,易求得
,,所以,,,故长轴长为 ,A错误;
焦距,B正确;将该椭圆还原成焦点在轴上的标准椭圆,其方程为 ,
设该椭圆焦点分别为,,点在该椭圆上,则 ,又由椭圆
定义可知, ,即
,解得 ,又
,所以的面积为,故C正确; ,
由椭圆的性质可知,当点为长轴的端点时,取得最大值,当点 为短轴的端
点时,取得最小值,故D正确.故选 .
11.已知函数对任意实数,都有 ,且
,则( )
A. B.
C.是一个周期为4的周期函数 D.
√
√
√
[解析] 由 ,得
,令 ,得
,则,A正确;令 ,得
,因此 ,则
,于是得,即 ,
,即函数 是周期为8的周期函数,C错误;
,B正确;又, ,
,, ,即
,因此
,D正确.故选 .
三、填空题:本题共3小题,每小题5分,共15分。
12.已知在等比数列中,, ,则数
列 的公比为___.
2
[解析] 设公比为 ,则
,
解得 .
13.汤圆是汉族传统小吃的代表之一,同时也是中国的传统节日元宵节最具有特色的食
物,表达了人民对幸福生活的一种向往和期盼.在广东省流行四式汤圆,这四式汤圆指
的是四种不同的馅:绿豆、红豆、糖冬瓜、芋头,小王在今年元宵节时,盛了一碗(10个)
汤圆,其中绿豆馅、红豆馅的汤圆各4个,糖冬瓜馅、芋头馅的各1个,则小王在碗里随
机取的4个汤圆中,吃到1个芋头馅的前提下,4个汤圆恰有4种馅的概率为___.
[解析] 记事件为“小王随机取的4个汤圆中有1个芋头馅的汤圆”,事件 为“小王随机取
的4个汤圆中恰有4种馅”,所以, ,所以
.
14.已知抛物线的焦点为,直线经过点交于,两点(点 在第一象限),
且,两点在的准线上的投影分别为,,准线与轴的交点为,分别记 与
的面积为,,若,则直线 的斜率为____.
[解析] 由题得 ,所以
,所以.如图,过点作 于
点,所以,设,则 ,则
,所以
,所以 ,所以直线 的斜率
.
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(本小题满分13分)
激光一体机是一种功能强大的办公设备,与传统的激光打印机相比,激光一体机还
集成了复印、扫描等多种功能,因此比传统的激光打印机更实用,从而近几年在全国各
地逐渐热销起来.下表为市统计的近5年该市激光一体机的销量,其中为年份代号,
(单位:万台)代表年销量.
年份 2021年 2021年 2022年 2023年 2024年
年份代号 1 2 3 4 5
年销量 万台 0.5 0.9 1 1.2 1.4
(1)经过分析,与线性相关,试求关于 的经验回归方程;
解: ,
,
(1分)
则 ,(4分)
,(5分)
所以关于的经验回归方程为 .(6分)
(2)利用(1)中所求方程,预测2025年该市激光一体机的销量;
解:2025年对应的年份代码 为6,
当时, (万台),
故可预测2025年该市激光一体机的销量约为1.63万台.(9分)
(3)某中学准备选购某型号的激光一体机供各办公室使用,下表是以往这种型号的激
光一体机的使用年限(整年)统计表:
使用年限 1年 2年 3年 4年 5年
该型号激光一体机(单位:台) 5 15 20 10 50
激光一体机使用年限越长,办公费用越低.以使用年限的频率估计概率,求该型号激光
一体机使用年限的分布列及数学期望 .
参考公式:, .
参考数据:, .
解:以频率估计概率,该型号激光一体机的使用年限 的分布列为:
1 2 3 4 5
0.05 0.15 0.2 0.1 0.5
(11分)
.(13分)
16.(本小题满分15分)
记数列的前项和为,已知, .
(1)求数列 的通项公式;
解:因为 ,
所以 ,
当时, ,
两式相减得 ,
整理得 ,
即 ,(4分)
又 ,
所以数列是以9为首项, 为公差的等差数列.(5分)
所以 .(6分)
(2)若,求数列的前项和 ;
解:由(1)得 ,(7分)
由,解得 .
所以当时, .(9分)
当时, .(10分)
所以 (11分)
(3)记,求数列的前项和 .
解:
,(13分)
所以
.(15分)
17.(本小题满分15分)
已知函数,且在 处取得极值.
(1)求的值及 的单调区间;
解:由题得 ,
由,解得 ,(2分)
此时, ,
令,得 ,
令,得 ,
故0是函数的极值点,
故 符合要求,(4分)
函数的单调递增区间是,单调递减区间是 .(5分)
(2)若存在,使得,求实数 的取值范围.
解:由 ,
可得 ,
则 ,(7分)
令 ,
则 ,
令 ,
则 ,(10分)
故当时,, 单调递增;
当时,, 单调递减,
而,,且时, ,
故当时, ,
当时, ,(12分)
故在上单调递减,在 上单调递增,
故 ,
因此,解得 ,
所以的取值范围为 .(15分)
18.(本小题满分17分)
已知双曲线的左、右焦点分别为,,,且点
到的渐近线的距离为,,为上在 轴上方的两点.
(1)求 的方程;
解:由题意知,得 .(1分)
因为点到直线的距离为 ,
所以 ,
又因为 ,
所以, ,(2分)
所以的方程为 .(3分)
(2)记的左顶点为,若直线与轴平行,证明:直线, 的斜率之积为定值;
解:由(1)知 ,
设,则, ,
所以 ,(5分)
因为 ,
所以 ,
所以直线,的斜率之积为定值 .(6分)
(3)若,求四边形 面积的取值范围.
解:根据对称性,设点在的左支上,点在 的右支上.
如图所示,延长交于点,延长交于点 ,
因为 ,
所以四边形为平行四边形,且面积为四边形 面积
的2倍,(7分)
易知直线 斜率不为0.
设,,直线, ,
由,消去 可得
,
恒成立,
所以, ,(9分)
所以,且
,(11分)
因为,所以 .(12分)
因为直线与间的距离为 ,(13分)
所以 ,(15分)
令, ,
所以 ,
因为在上单调递减,且 ,
所以在 上单调递增,
当,即时,四边形 的面积取得最小值,最小值为48,
所以四边形面积的取值范围为 .(17分)
19.(本小题满分17分)
如图,四边形是边长为2的正方形,点,分别在线段, 上运动,且
.将沿折起,使得点到达点的位置,此时平面 平面 .
(1)当为 的中点时,
(ⅰ)证明: ;
解:当为的中点时,为的中点,此时, ,
.
如图,取的中点,连接, ,
则, ,
又,, 平面 ,
所以 平面 ,
又 平面 ,
所以 .(4分)
(ⅱ)求点到平面 的距离.
解:设点到平面的距离为 ,
,
因为平面 平面,平面 平面, ,
所以 平面 ,
因为 平面 ,
所以 ,
则 ,
所以 ,
所以 ,
.(7分)
由 ,
得 ,
所以 ,
即点到平面的距离为 .(8分)
(2)证明:存在点,使得二面角的平面角为 .
[答案] 如图,以点为坐标原点,, 所
在直线分别为, 轴建立如下图所示的空间
直角坐标系,
过点在平面内作,连接 ,
由已知可得, ,
, ,
故 ,
则 ,
即,且 ,
因为平面 平面,平面
平面, 平面 ,
所以 平面 ,
设, ,
则 , ,
因为 ,
则 ,
,
易得 ,
则点,, ,
, ,
设平面的一个法向量为 ,则
,(12分)
令 ,可得 ,
易知平面的一个法向量为 ,
,
因为 ,
令,
,
可得
,
即 ,(14分)
所以
,
令 ,
令
,
易知函数在 上连续,
因为, ,
由零点存在性定理可知,存在,使得 ,
因此,存在点,使得二面角的的平面角为 .(17分)
同课章节目录
