9.4平行线的判定习题课件(22张PPT)
文档属性
| 名称 | 9.4平行线的判定习题课件(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 281.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-29 23:00:55 | ||
图片预览





文档简介
课件22张PPT。9.4平行线的判定
习题课1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
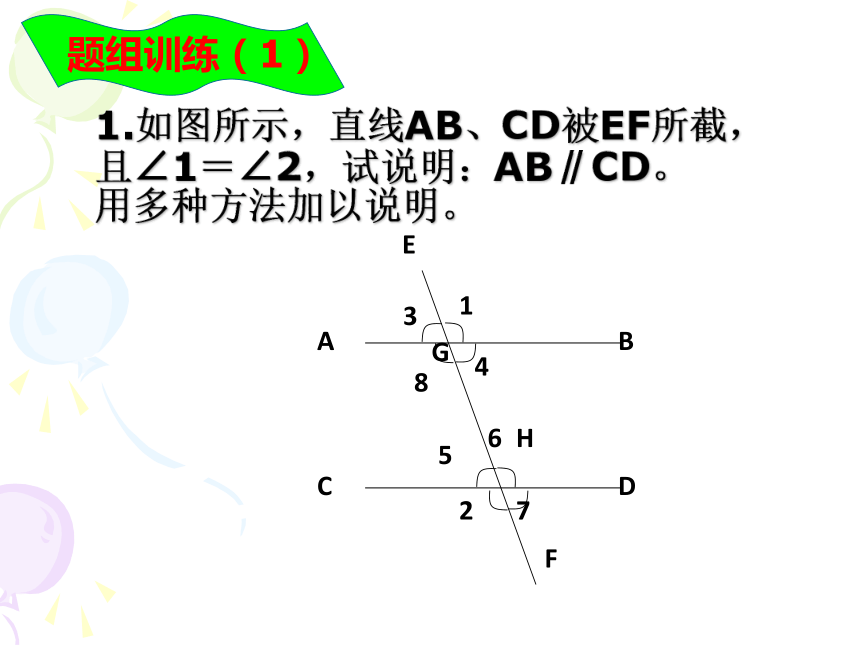
5.平行线的定义.判定两条直线是否平行的方法有:归纳知识: 1.如图所示,直线AB、CD被EF所截,且∠1=∠2,试说明:AB∥CD。 用多种方法加以说明。题组训练(1)2.看图填空,根据题意,识别哪两条直线平行。
⑴如果∠1=∠2,那么根据 可得 。
⑵如果∠3=∠4,那么根据 可得 。
⑶如果∠6=∠7,那么根据 可得 。
⑷如果∠DAB+∠ADC=180°,那么根据 可得 。
⑸如果∠CBE=∠DAB,那么根据 可得 。
⑹如果∠ABC+∠BCD=180°,那么根据 可得 。题组训练(1)(变式)如图所示,已知∠1=∠2,BD平分∠ABC,可推出哪两条线段平行?写出推理过程,如要推出另两条线段平行,则应将以上两条件之一作如何改变?
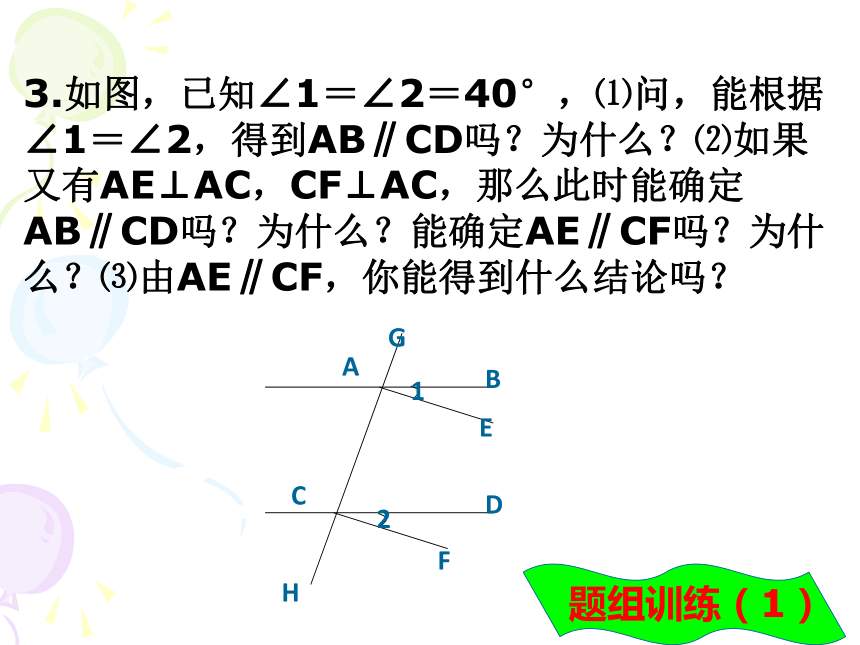
题组训练(1)3.如图,已知∠1=∠2=40°,⑴问,能根据∠1=∠2,得到AB∥CD吗?为什么?⑵如果又有AE⊥AC,CF⊥AC,那么此时能确定AB∥CD吗?为什么?能确定AE∥CF吗?为什么?⑶由AE∥CF,你能得到什么结论吗?
?
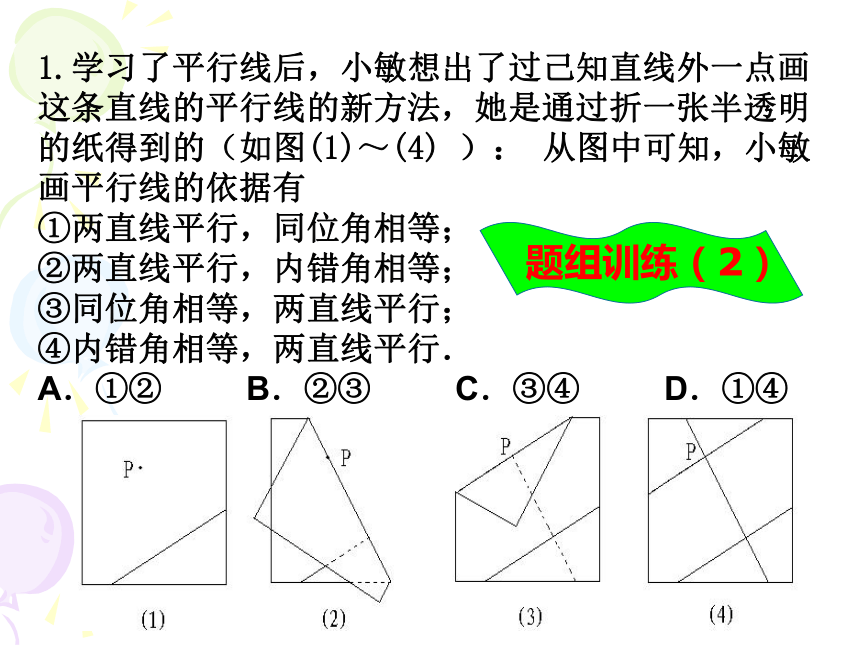
题组训练(1)1.学习了平行线后,小敏想出了过己知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4) ): 从图中可知,小敏画平行线的依据有
①两直线平行,同位角相等; ②两直线平行,内错角相等;
③同位角相等,两直线平行; ④内错角相等,两直线平行.
A.①② B.②③ C.③④ D.①④题组训练(2)2.一辆汽车在笔直的高速公路上行驶,两次拐弯后仍在原来的方向上平行前进,那么,这两次拐弯的角度可能是 ( )
A.第一次向右拐80°,第二次向左拐100°
B.第一次向左拐80°,第二次向右拐80°
C.第一次向左拐80°,第二次向右拐100°
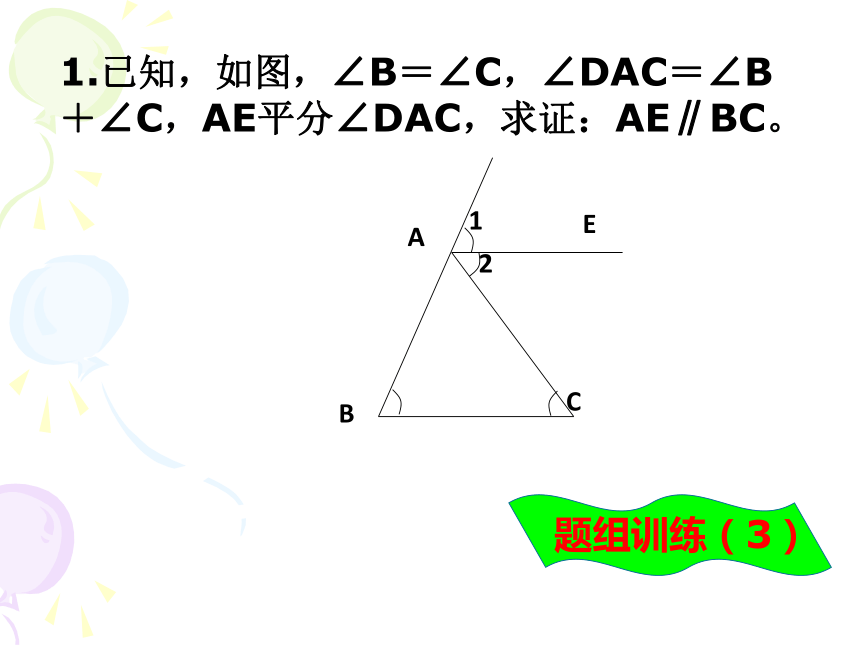
D.第一次向右拐80°,第二次向右拐80°题组训练(2)1.已知,如图,∠B=∠C,∠DAC=∠B+∠C,AE平分∠DAC,求证:AE∥BC。题组训练(3)2.已知∠2=3∠1,且∠3+∠1=90°,
试说明AB∥BC。
2题组训练(3)3.已知,∠BAF=46°,∠ACE=136°,CE⊥CD。试推理说明:CD∥AB。
?
题组训练(3)1.如图,∠1与∠D互余,CE⊥DE,直线AB与CD平行吗?为什么?
BA1CDE题组训练(4)2.∠C+∠A=∠AEC,判断AB与CD
是否平行并说明理由 题组训练(4)3.如图∠A+∠B+∠C+∠D=360°,且∠A=∠C,∠B=∠D,
那么AB∥CD ,AD∥BC.请说明理由。
D
A
B
C
?
题组训练(4)4、如图,已知∠1=115°,∠2=50°,∠3=65°,又EG为∠NEF的平分线,说明:AB∥CD,EG∥GH。题组训练(4)1.如图, 已知直线a1, a2, a3被直线 a 所截,∠1=72°,
∠2=108°, ∠3=72°,说明a1∥a2∥a3的理由.123题组训练(5)2.如图所示,∵∠ADE=∠DEF(已知)
∴AD∥ ( )
又 ∵∠EFC+∠C=180°(已知)
∴EF∥ ( )
∴ ∥ ( )
题组训练(5)(变式)如图所示,依据图形找出能使AD∥BC成立的条件(至少6个)。题组训练(5)3.如图,∠1=∠C,∠2+∠C=180°,AB与EF平行吗?为什么? FE题组训练(5)1.如图,已知QR平分∠PQN,NR平分∠PQN(已知),∠1+∠2=90°,求证:PQ∥MN。
证明:∵QR平分∠PQN(已知)
∴∠PQM=2∠1( )
又 ∵NR平分∠QNM(已知)
∴∠QNM=2∠2
又 ∵∠1+∠2=90°(已知)、
∴∠PQN+∠QNM= =180°
∴ ∥ ( )
题组训练(6)2.如图,在长方形的台球桌面上,∠2+∠3=90°,∠1=∠2,∠3=∠4,那么AC与BD平行吗?
?
题组训练(6)3.实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射.若被b反射出的光线n与光线m平行,且∠1=50°,则∠2= °,∠3= °.
(2)在(1)中,若∠1=55°,则∠3= °;若∠1=40°,则∠3= °.
(3)由(1)、(2),请你猜想:当两平面镜a、b的夹角∠3= °时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行.你能说明理由吗?
?
题组训练(6)
习题课1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
5.平行线的定义.判定两条直线是否平行的方法有:归纳知识: 1.如图所示,直线AB、CD被EF所截,且∠1=∠2,试说明:AB∥CD。 用多种方法加以说明。题组训练(1)2.看图填空,根据题意,识别哪两条直线平行。
⑴如果∠1=∠2,那么根据 可得 。
⑵如果∠3=∠4,那么根据 可得 。
⑶如果∠6=∠7,那么根据 可得 。
⑷如果∠DAB+∠ADC=180°,那么根据 可得 。
⑸如果∠CBE=∠DAB,那么根据 可得 。
⑹如果∠ABC+∠BCD=180°,那么根据 可得 。题组训练(1)(变式)如图所示,已知∠1=∠2,BD平分∠ABC,可推出哪两条线段平行?写出推理过程,如要推出另两条线段平行,则应将以上两条件之一作如何改变?
题组训练(1)3.如图,已知∠1=∠2=40°,⑴问,能根据∠1=∠2,得到AB∥CD吗?为什么?⑵如果又有AE⊥AC,CF⊥AC,那么此时能确定AB∥CD吗?为什么?能确定AE∥CF吗?为什么?⑶由AE∥CF,你能得到什么结论吗?
?
题组训练(1)1.学习了平行线后,小敏想出了过己知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4) ): 从图中可知,小敏画平行线的依据有
①两直线平行,同位角相等; ②两直线平行,内错角相等;
③同位角相等,两直线平行; ④内错角相等,两直线平行.
A.①② B.②③ C.③④ D.①④题组训练(2)2.一辆汽车在笔直的高速公路上行驶,两次拐弯后仍在原来的方向上平行前进,那么,这两次拐弯的角度可能是 ( )
A.第一次向右拐80°,第二次向左拐100°
B.第一次向左拐80°,第二次向右拐80°
C.第一次向左拐80°,第二次向右拐100°
D.第一次向右拐80°,第二次向右拐80°题组训练(2)1.已知,如图,∠B=∠C,∠DAC=∠B+∠C,AE平分∠DAC,求证:AE∥BC。题组训练(3)2.已知∠2=3∠1,且∠3+∠1=90°,
试说明AB∥BC。
2题组训练(3)3.已知,∠BAF=46°,∠ACE=136°,CE⊥CD。试推理说明:CD∥AB。
?
题组训练(3)1.如图,∠1与∠D互余,CE⊥DE,直线AB与CD平行吗?为什么?
BA1CDE题组训练(4)2.∠C+∠A=∠AEC,判断AB与CD
是否平行并说明理由 题组训练(4)3.如图∠A+∠B+∠C+∠D=360°,且∠A=∠C,∠B=∠D,
那么AB∥CD ,AD∥BC.请说明理由。
D
A
B
C
?
题组训练(4)4、如图,已知∠1=115°,∠2=50°,∠3=65°,又EG为∠NEF的平分线,说明:AB∥CD,EG∥GH。题组训练(4)1.如图, 已知直线a1, a2, a3被直线 a 所截,∠1=72°,
∠2=108°, ∠3=72°,说明a1∥a2∥a3的理由.123题组训练(5)2.如图所示,∵∠ADE=∠DEF(已知)
∴AD∥ ( )
又 ∵∠EFC+∠C=180°(已知)
∴EF∥ ( )
∴ ∥ ( )
题组训练(5)(变式)如图所示,依据图形找出能使AD∥BC成立的条件(至少6个)。题组训练(5)3.如图,∠1=∠C,∠2+∠C=180°,AB与EF平行吗?为什么? FE题组训练(5)1.如图,已知QR平分∠PQN,NR平分∠PQN(已知),∠1+∠2=90°,求证:PQ∥MN。
证明:∵QR平分∠PQN(已知)
∴∠PQM=2∠1( )
又 ∵NR平分∠QNM(已知)
∴∠QNM=2∠2
又 ∵∠1+∠2=90°(已知)、
∴∠PQN+∠QNM= =180°
∴ ∥ ( )
题组训练(6)2.如图,在长方形的台球桌面上,∠2+∠3=90°,∠1=∠2,∠3=∠4,那么AC与BD平行吗?
?
题组训练(6)3.实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射.若被b反射出的光线n与光线m平行,且∠1=50°,则∠2= °,∠3= °.
(2)在(1)中,若∠1=55°,则∠3= °;若∠1=40°,则∠3= °.
(3)由(1)、(2),请你猜想:当两平面镜a、b的夹角∠3= °时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行.你能说明理由吗?
?
题组训练(6)
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
