第七章数据的收集、整理与描述同步练习(含解析)
文档属性
| 名称 | 第七章数据的收集、整理与描述同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 718.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 14:57:47 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第七章数据的收集、整理与描述
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某校对七年级学生上学方式进行了统计,并绘制了如图所示的统计图,则“步行”对应扇形的圆心角度数为( )
A. B. C. D.
2.为推广和普及冰雪运动,某中学举办“青春梦想,活力飞Young”冬奥知识竞赛.为了了解全校2800名学生的竞赛成绩,从中抽取了100名学生的竞赛成绩进行统计分析,以下说法正确的是( )
A.抽取的100名学生是总体的一个样本 B.每名学生的竞赛成绩是个体
C.全校2800名学生是总体 D.100名学生是样本容量
3.下列调查中,最适合进行抽样调查的是( )
A.对搭乘高铁的乘客进行安全检查 B.调查某市中学生的视力情况
C.审核书稿中的错别字 D.调查某班同学防溺水安全知识学习情况
4.有40个数据,其中最大值为35,最小值为16,在绘制频数直方图时,若取组距为4,则应该分的组数是( )
A.5 B.6 C.7 D.8
5.下列调查方式,你认为最合适的是( )
A.旅客上飞机前的安检,采用抽样调查方式
B.了解某地区饮用水矿物质含量的情况,采用抽样调查方式
C.调查某种品牌笔芯的使用寿命,采用全面调查方式
D.调查湖南卫视《会画少年的天空》节目的收视率,采用全面调查方式
6.神舟十九号载人飞船在酒泉卫星发射中心点火发射,神舟十九号航天员乘组顺利进驻中国空间站,关于此次发射任务,不适合做全面调查的是( )
A.调查神舟十九号载人飞船的零部件是否符合标准
B.调查三位宇航员的身体状况
C.调查宇航员的太空服是否符合安全标准
D.调查神舟十九号载人飞船发射时的收视率
7.随着中国经济的高速发展,人们的生活水平发生了巨大改变,目前大部分中小学生的营养问题已经从以前的营养不良变成营养过剩.某中学从该校的4000名学生中随机抽取了400名学生进行体重调查,下列说法错误的是( )
A.总体是该校4000名学生的体重 B.个体是每一个学生
C.样本是抽取的400名学生的体重 D.样本容量是400
8.某校为了了解全校学生对“智能杭州”的了解程度,随机抽取了部分学生进行问卷调查,并根据收集的信息进行了统计,绘制了下面尚不完整的统计图.根据以上的信息,给出下列判断:①参加问卷调查的学生有50人;②参加问卷调查的学生中,“基本了解”的有10人;③扇形图中“基本了解”部分的扇形的圆心角的度数是;④在参加问卷调查的学生中,“了解”的学生人数占10%.其中结论正确的序号是( )
A.①②③ B.①②④ C.①③④ D.②③④
9.为了解某校七年级名学生的身高,从中抽取了名学生对其身高进行统计分析,以下说法正确的是( )
A.800名学生是总体 B.每个学生是个体
C.每个学生的身高是个体 D.样本容量是名
10.牛奶中含有丰富的营养成分,其中水分约占82%,蛋白质约占4.3%,脂肪约占6%,乳糖约占7%,其他约占0.7%,对人体的健康有非常重要的作用.为直观地表示出各成分在总体中所占的百分比,最合适的统计图是( )
A.折线统计图 B.条形统计图 C.扇形统计图 D.频数分布直方图
11.某红十字会对50名志愿者进行血型统计,列出如下统计表,则50名志愿者中B型血的人数是( )
组别 A型 B型 AB型 O型
百分比 30% 20% 10% 40%
A.5 B.10 C.15 D.20
12.为了了解我县初一2300名学生在疫情期间“数学空课”的学习情况,全县组织了一次数学检测,从中抽取150名考生的成绩进行统计分析,以下说法正确的是( )
A.这150名考生是总体的一个样本 B.2300名考生是总体
C.每位学生的数学成绩是个体 D.150名学生是样本容量
二、填空题
13.如图是根据我县教育局网站上公布的某初中为玉树地震灾区捐款的情况而制作的统计图,已知该校在校学生有人,请根据统计图计算该校共捐款 元.
14.为了调查夏季冷饮市场上的一批冰淇淋的质量情况,适宜的调查方式是 .
15.某校八年级200名学生参加生命安全知识测试,测试分数均大于或等于60且小于100,分数段的频率分布情况如表所示(其中每个分数段可包括最小值,不包括最大值),结合表的信息,可测得测试分数在分数段的学生有 名.
分数段
频率
16.某校为了解七年级学生对“七步洗手法”的掌握情况,现在800名七年级学生中随机抽取60名学生进行调查,则此次调查的样本容量是 .
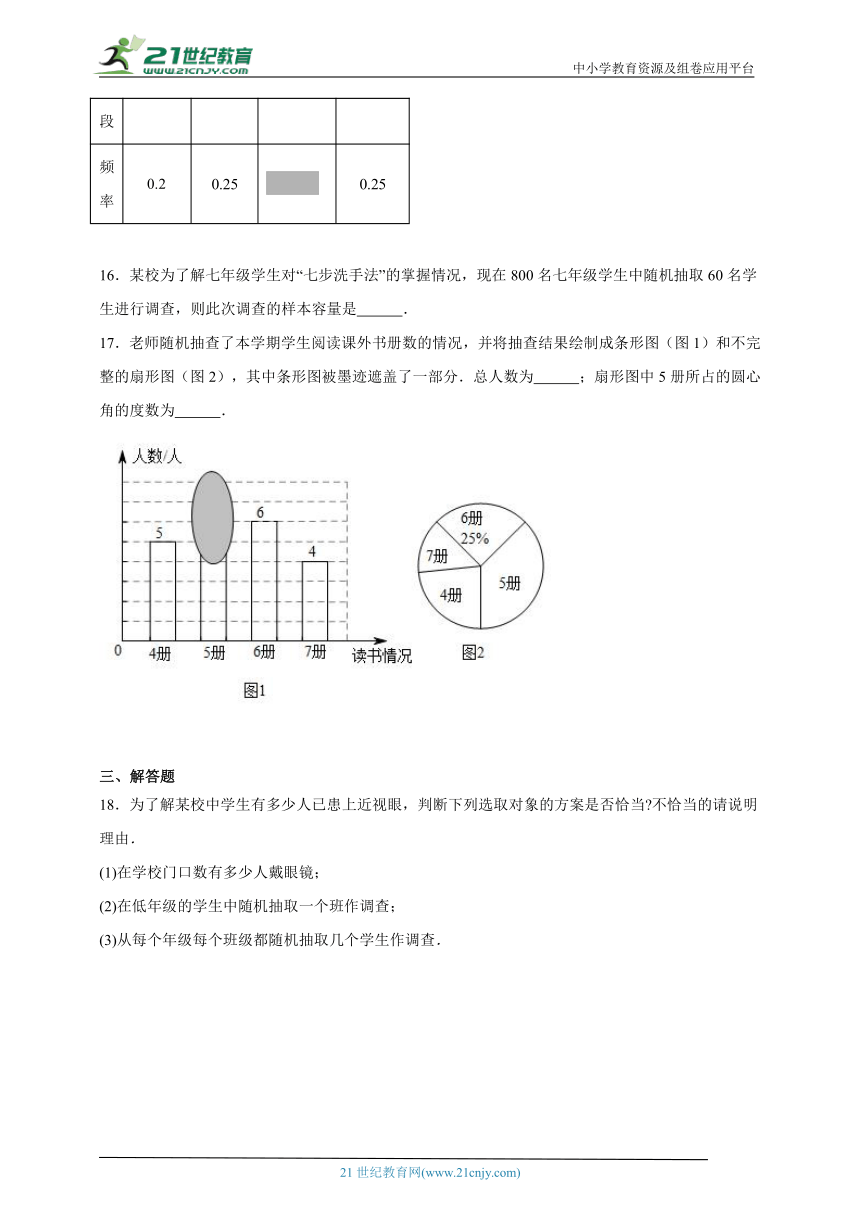
17.老师随机抽查了本学期学生阅读课外书册数的情况,并将抽查结果绘制成条形图(图1)和不完整的扇形图(图2),其中条形图被墨迹遮盖了一部分.总人数为 ;扇形图中5册所占的圆心角的度数为 .
三、解答题
18.为了解某校中学生有多少人已患上近视眼,判断下列选取对象的方案是否恰当 不恰当的请说明理由.
(1)在学校门口数有多少人戴眼镜;
(2)在低年级的学生中随机抽取一个班作调查;
(3)从每个年级每个班级都随机抽取几个学生作调查.
19.判断下面这几个抽样调查选取样本的方法是否合适,并说明理由.
(1)为了解全班同学期末考试的平均成绩,老师抽查了前5名同学的平均成绩;
(2)教育部为了调查全国中小学乱收费情况,调查了某市所有中小学;
(3)某兴趣小组为了解本校1 800名学生的视力情况,随机抽查了本校九年级学生中50名学生的视力情况.
20.请指出下列抽样调查中的总体、个体、样本和样本容量
(1)为了解某所学校的学生参加课外体育活动的时间,调查了其中20名学生每天参加课外体育活动的时间;
(2)为了解某公园一年中平均每天进园的人数,对其中30天进园的人数进行了统计;
(3)为了解八年级学生的视力情况,学校从八年级随机抽取44名学生进行视力检查.
21.某校为了解落实“双减”政策后学生每天完成书面作业的时间t(单位:分钟)的情况,在全校随机抽取部分小学生进行调查,按四个组别进行整理,绘制成如下两幅不完整的统计图表,请根据图表信息解答下列问题:
抽取的学生作业时间统计表
组别 调查结果 人数(人)
A 120
B a
C 180
D 90
(1)这次调查抽取学生的总人数是_______,B组的学生人数______;
(2)该校共有学生1500人,请估算该校每日书面作业时间不少于90分钟的学生人数;
(3)请结合数据对该校“双减”工作提出一条合理性建议.
22.下列抽样调查中所选的样本合适吗?
(1)张老师为了解全班50名学生对英语单词的掌握情况,抽取5名学生进行检查;
(2)为了解全校26个班的课外活动情况,从七年级中抽取两个班进行分析;
(3)为调查全市中学生的上网情况,在全市的300所中学中随意抽取50所学校的学生进行调查;
(4)为了解我国中学多媒体的普及情况,在北京市做了抽样调查.
23.小丽同学本学期由于努力学习,数学成绩稳步提高.下表为小丽同学本学期近5次数学考试成绩:
第1次 第2次 第3次 第4次 第5次
成绩/分 80 85 85 90 90
(1)补全折线图:
(2)已知第6次数学考试的难度与前5次相当,根据上面数据,请你预测一下小丽第6次的数学考试成绩可能会是多少分,并说明你的理由(言之有理即可).
24.某校八年级有800名学生,从中随机抽取了名学生进行立定跳远测试,指出下列说法中哪些是正确的.
(1)这种调查方式是抽样调查.
(2)800名学生是总体.
(3)每名学生的立定跳远成绩是个体.
(4)这名学生的立定跳远成绩是总体的一个样本.
(5)名学生是样本容量.
《第七章数据的收集、整理与描述》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B B A B D B C C C
题号 11 12
答案 B C
1.C
【分析】本题考查了扇形统计图圆心角度数的算法,熟练掌握圆心角度数的算法是解决本题的关键.用乘以步行所占百分比即可.
【详解】解:由题意可得,步行所在的扇形圆心角的度数:
.
故选:C.
2.B
【分析】根据样本(被抽取的个体组成一个样本)、个体(组成总体的每一个考查对象)、总体(要考查的全体对象)、样本容量的定义(样本中个体的数目称为样本容量)逐项判断即可得.
【详解】解:A、抽取的100名学生的竞赛成绩是总体的一个样本,则此项错误,不符合题意;
B、每名学生的竞赛成绩是个体,则此项正确,符合题意;
C、全校2800名学生的竞赛成绩是总体,则此项错误,不符合题意;
D、样本容量是100,则此项错误,不符合题意;
故选:B.
【点睛】本题考查了样本、个体、总体、样本容量,熟记各概念是解题关键.
3.B
【分析】本题考查了全面调查与抽样调查,熟练掌握全面调查与抽样调查的特点是解题的关键.根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似判断即可.
【详解】解:A. 对搭乘高铁的乘客进行安全检查,适合全面调查,故A不符合题意;
B. 调查某市中学生的视力情况,适合抽样调查,故B符合题意;
C. 审核书稿中的错别字,适合全面调查,故C不符合题意;
D. 调查某班同学防溺水安全知识学习情况,适合全面调查,故D不符合题意;
故选:B.
4.A
【分析】本题考查了数据分组的方法,熟练掌握组数与极差和组距的关系是解题的关键.
求得最大值与最小值的差,除以组距就是组数.
【详解】(组)
故选:A
5.B
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
【详解】A、旅客上飞机前的安检,应该采用全面调查方式,不合题意;
B、了解某地区饮用水矿物质含量的情况,采用抽样调查方式,符合题意;
C、调查某种品牌笔芯的使用寿命,应该采用抽样调查方式,不合题意;
D、调查湖南卫视《会画少年的天空》节目的收视率,应该采用抽样调查方式,不合题意;
故选:B.
【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查,事关重大的调查往往选用普查.
6.D
【分析】本题考查的是全面调查和抽样调查,根据全面调查和抽样调查的概念判断即可.通过普查可以直接得到较为全面、可靠的信息,但花费的时间较长,耗费大,且一些调查项目并不适合普查.其一,调查者能力有限,不能进行普查.其二,调查过程带有破坏性.其三,有些被调查的对象无法进行普查.
【详解】解:A、查神舟十九号载人飞船的零部件是否符合标准,适合做全面调查,不符合题意;
B、调调查三位宇航员的身体状况,适合做全面调查,不符合题意;
C、调查宇航员的太空服是否符合安全标准,适合做全面调查,不符合题意;
D、调查神舟十九号载人飞船发射时的收视率,不适合做全面调查,符合题意.
故选:D.
7.B
【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
【详解】解:A.总体是该校4000名学生的体重,说法正确,故A不符合题意;
B.个体是每一个学生的体重,原来的说法错误,故B符合题意;
C.样本是抽取的400名学生的体重,说法正确,故C不符合题意;
D.样本容量是400,说法正确,故D不符合题意.
故选:B.
【点睛】本题主要考查了总体、个体、样本、样本容量,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
8.C
【分析】本题考查了两种统计图的认识,解题的关键是正确的利用这两种统计图的关系.
①用了解很少的学生数除以该组所占比例即可得到总人数; ②用学生总数乘以该组所占的比例得到基本了解的学生数;③扇形所对圆心角的度数等于圆周角乘以该组所占比例.
【详解】解:①∵了解很少的学生有25人,占学生总数的,
∴参加问卷调查的学生有人,故①正确;
②人,
∴参加进行问卷调查的学生中,“基本了解”的有15人,故②错误;
③,
∴“基本了解”部分的扇形的圆心角的度数是,故③正确;
“了解”的学生有,占比为,故④正确;
故选C.
9.C
【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目,据此逐项判断即可得出结论.
【详解】A、800名学生的身高是总体,故此选项错误,不符合题意;
B、每个学生的身高是个体,故此选项错误,不符合题意;
C、每个学生的身高是个体,故此选项正确,符合题意;
D、样本容量是,不带单位,故此选项错误,不符合题意;
故选:C.
【点睛】本题考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象,总体、个体与样本的考查对象是相同的,所不同的是范围的大小,样本容量是样本中包含的个体的数目,不能带单位.
10.C
【分析】对各种统计图优势的理解,根据题意选择合适的统计图即可.
【详解】扇形统计图能很好的表示部分与整体之间的关系.所以为直观地表示出各成分在总体中所占的百分比,最合适的统计图是扇形统计图.
故选:C
【点睛】本题考查对各种统计图优势的理解,根据题意选择合适的统计图即可.
11.B
【分析】利用数据统计表中对应的百分比计算即可.
【详解】解:
故选:B.
【点睛】本题考查数据统计中统计表,百分比的意义,理解百分比的意义是解题的关键.
12.C
【分析】总体是指考查对象的全体,个体是总体中的每一个考查对象.样本是指总体中所抽取的部分个体,样本容量是指样本中个体的数目,据此求解即可.
【详解】总体是我县初一2300名学生在疫情期间“数学空课”的学习情况 ;
样本是这150名考生在疫情期间“数学空课”的学习情况;
个体是每位学生的数学成绩;
样本容量是150.
故选:C.
【点睛】本题主要考查了总体、个体、样本和样本容量的定义,解题要分清具体问题中的总体、个体与样本的区别,关键是明确考查对象的范围.样本容量只是个数字,没有单位.
13.12590
【分析】根据扇形统计图中的数据求出各年级人数,再根据条形统计图中的数据求出各年级捐款数,各年级相加即可得到该校捐款总数.
【详解】解:1000×32%×15=4800元;
1000×33%×13=4290元;
1000×35%×10=3500元;
∴该校学生共捐款4800+4290+3500=12590元.
故答案为:12590.
【点睛】此题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
14.抽样调查
【分析】调查对象数量众多,可操作性低,耗时耗力的情况下,应采用抽样调查.
【详解】解:该冰淇淋可能销往世界各地,消费者众多,若采用全面调查不易操作,且耗时耗力;
故应采用抽样调查的方式.
故答案为:抽样调查
【点睛】本题考查抽样调查的适用特点.熟悉特点是解题关键.
15.60
【分析】先根据表格求出频率,再用总数乘以频率进行求解即可得到答案.
【详解】解:由表格可知,测试分数在分数段的学生的频率为,
所以,测试分数在分数段的学生人数为(名),
故答案为:60.
【点睛】本题考查了频数与频率,解题关键是掌握频率频数总数.
16.60
【分析】根据样本容量:“抽取的样本中的数量”,作答即可.注意样本容量不带单位.
【详解】解:由题意,此次调查的样本容量是60;
故答案为:60.
17. 24 135°/135度
【分析】由6册人数及其所占百分比求出总人数,再根据各册数的人数和等于总人数可得5册人数,用360°乘以对应人数所占比例即可得.
【详解】解:∵被调查的总人数为6÷25%=24(人),
∴5册的人数为24-(5+6+4)=9(人),
扇形图中5册所占的圆心角的度数为360°×=135°,
故答案为:24;135°.
【点睛】此题考查了条形统计图与扇形统计图的知识.注意掌握条形统计图与扇形统计图各量的对应关系是解此题的关键.
18.(1)不恰当,理由见解析
(2)不恰当,理由见解析
(3)恰当
【分析】根据选取的样本是否具有代表性依次判断即可求解.
【详解】(1)不恰当;因为可能有住校学生没调查到.
(2)不恰当;因为低年级学生的视力一般比高年级学生好.
(3)样本具有代表性,因此恰当.
【点睛】本题考查了样本的代表性,解题关键是掌握选取的样本应该具有代表性,要求学生能根据实际情况进行判断.
19.(1)不合适,理由见解析
(2)不合适,理由见解析
(3)不合适,理由见解析
【分析】本题考查了样本的选取,解题的关键是要考虑样本具有广泛性与代表性,所谓代表性,就是抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
(1)前5名同学成绩的平均数不能代表全班同学期末考试的平均成绩,不具有代表性,由此即可解答;
(2)某市所有中小学乱收费情况的数据不能代表全国中小学乱收费情况,不具有广泛性和代表性,由此即可解答;
(3)本校九年级学生中50名学生的视力情况不能代表本校1 800名学生的视力情况,不具有代表性,由此即可解答.
【详解】(1)不合适,前5名同学成绩的平均数会大于整个班级同学成绩的平均数,这样,样本就不具有代表性了.
(2)不合适,样本虽然足够大,但遗漏了其他地区的这些群体,应该在全国范围内选取样本.此外,将某市所有中小学乱收费情况作为样本是没有必要的.
(3)不合适,本校九年级学生视力情况的调查结果不能代表本校全部学生的视力情况,应该从全校各年级的学生中随机抽查.
20.(1)见解析
(2)见解析
(3)见解析
【分析】本题考查了总体、个体、样本、样本容量的知识,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
(1)根据总体、个体、样本、样本容量的定义,进行判断即可;
(2)根据总体、个体、样本、样本容量的定义,进行判断即可;
(3)根据总体、个体、样本、样本容量的定义,进行判断即可.
【详解】(1)解:总体:该校学生参加课外体育活动的时间;
个体:每位学生参加课外体育活动的时间;
样本:20名学生每天参加课外体育活动的时间;
样本容量:20;
(2)解:总体:该公园一年中平均每天进园的人数;
个体:每天进园的人数;
样本:其中30天进园的人数;
样本容量:30;
(3)解:总体:八年级学生的视力情况;
个体:每个学生的视力情况;
样本:44名学生的视力情况;
样本容量:44.
21.(1)600,210
(2)该校每日作业时长不少于90分钟的学生人数为675人
(3)建议该学校作业布置要减少题量或降低难度.(答案不唯一)
【分析】(1)根据总人数=A组人数÷A组所占百分比,总人数×B组百分比,即可求出本题答案;(2)1500×不低于90分钟学生的百分比,即可求出结果;(3)合理即可.
【详解】(1)这次调查抽取学生的总人数是600,B组的学生人数;
故答案为:600,210;
(2)(人),
答:该校每日作业时长不少于90分钟的学生人数为675人;
(3)该校每日作业时长不少于90分钟的学生人数占比高达45%,建议该学校作业布置要减少题量或降低难度.(答案不唯一,理由合理即可,没有结合数据得1分)
【点睛】本题考查统计表和扇形统计图,考查数据处理和分析的能力,解题关键在从不同的图中读出相应的统计量.
22.(1)不合适
(2)不合适
(3)合适
(4)不合适
【分析】根据抽取样本的方法进行判断即可:抽取样本时就是要考虑样本具有广泛性与代表性,所谓代表性,就是抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
【详解】(1)解:抽样较少,不能反映出全班学生对英语单词的掌握情况,所以所选样本不合适.
(2)解:从七年级抽取两个班不具有代表性,所以所选样本不合适.
(3)解:由于抽样是随机的,且数量适中,所以所选样本比较合适.
(4)解:抽取的样本具有片面性,不具有代表性,所以所选样本不合适.
【点睛】本题考查抽样调查的可靠性,样本具有代表性是指抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
23.(1)见解析
(2)95分,见解析
【分析】本题考查了折线统计图的作图,应用,熟练掌握统计图的意义是解题的关键.
(1)根据折线图画图方法,完善图即可.
(2)根据折线图的发展趋势,可以预测提升5分,解答即可.
【详解】(1)小丽同学本学期近5次数学考试成绩折线图如答图.
(2)解:预测小丽第6次的数学考试成绩为95分.
理由:由折线规律发现,小丽同学本学期近5次数学考试成绩稳步提升,第6次测验的难度与前5次相当,所以这次数学成绩可能提高5分,成绩为95分.
24.(1)正确
(2)错误
(3)正确
(4)正确
(5)错误
【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
【详解】(1)解:八年级有800名学生,从中随机抽取了100名学生进行立定跳远测试,是抽样调查,故(1)正确;
(2)800名学生的立定跳远成绩是总体,故(2)错误;
(3)每名学生的立定跳远成绩是个体,故(3)正确;
(4)这100名学生的立定跳远成绩是总体的一个样本,故(4)正确;
(5)100是样本容量,故(5)错误.
【点睛】本题考查了总体、个体、样本、样本容量、抽样调查与全面调查等概念,掌握这些概念是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第七章数据的收集、整理与描述
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某校对七年级学生上学方式进行了统计,并绘制了如图所示的统计图,则“步行”对应扇形的圆心角度数为( )
A. B. C. D.
2.为推广和普及冰雪运动,某中学举办“青春梦想,活力飞Young”冬奥知识竞赛.为了了解全校2800名学生的竞赛成绩,从中抽取了100名学生的竞赛成绩进行统计分析,以下说法正确的是( )
A.抽取的100名学生是总体的一个样本 B.每名学生的竞赛成绩是个体
C.全校2800名学生是总体 D.100名学生是样本容量
3.下列调查中,最适合进行抽样调查的是( )
A.对搭乘高铁的乘客进行安全检查 B.调查某市中学生的视力情况
C.审核书稿中的错别字 D.调查某班同学防溺水安全知识学习情况
4.有40个数据,其中最大值为35,最小值为16,在绘制频数直方图时,若取组距为4,则应该分的组数是( )
A.5 B.6 C.7 D.8
5.下列调查方式,你认为最合适的是( )
A.旅客上飞机前的安检,采用抽样调查方式
B.了解某地区饮用水矿物质含量的情况,采用抽样调查方式
C.调查某种品牌笔芯的使用寿命,采用全面调查方式
D.调查湖南卫视《会画少年的天空》节目的收视率,采用全面调查方式
6.神舟十九号载人飞船在酒泉卫星发射中心点火发射,神舟十九号航天员乘组顺利进驻中国空间站,关于此次发射任务,不适合做全面调查的是( )
A.调查神舟十九号载人飞船的零部件是否符合标准
B.调查三位宇航员的身体状况
C.调查宇航员的太空服是否符合安全标准
D.调查神舟十九号载人飞船发射时的收视率
7.随着中国经济的高速发展,人们的生活水平发生了巨大改变,目前大部分中小学生的营养问题已经从以前的营养不良变成营养过剩.某中学从该校的4000名学生中随机抽取了400名学生进行体重调查,下列说法错误的是( )
A.总体是该校4000名学生的体重 B.个体是每一个学生
C.样本是抽取的400名学生的体重 D.样本容量是400
8.某校为了了解全校学生对“智能杭州”的了解程度,随机抽取了部分学生进行问卷调查,并根据收集的信息进行了统计,绘制了下面尚不完整的统计图.根据以上的信息,给出下列判断:①参加问卷调查的学生有50人;②参加问卷调查的学生中,“基本了解”的有10人;③扇形图中“基本了解”部分的扇形的圆心角的度数是;④在参加问卷调查的学生中,“了解”的学生人数占10%.其中结论正确的序号是( )
A.①②③ B.①②④ C.①③④ D.②③④
9.为了解某校七年级名学生的身高,从中抽取了名学生对其身高进行统计分析,以下说法正确的是( )
A.800名学生是总体 B.每个学生是个体
C.每个学生的身高是个体 D.样本容量是名
10.牛奶中含有丰富的营养成分,其中水分约占82%,蛋白质约占4.3%,脂肪约占6%,乳糖约占7%,其他约占0.7%,对人体的健康有非常重要的作用.为直观地表示出各成分在总体中所占的百分比,最合适的统计图是( )
A.折线统计图 B.条形统计图 C.扇形统计图 D.频数分布直方图
11.某红十字会对50名志愿者进行血型统计,列出如下统计表,则50名志愿者中B型血的人数是( )
组别 A型 B型 AB型 O型
百分比 30% 20% 10% 40%
A.5 B.10 C.15 D.20
12.为了了解我县初一2300名学生在疫情期间“数学空课”的学习情况,全县组织了一次数学检测,从中抽取150名考生的成绩进行统计分析,以下说法正确的是( )
A.这150名考生是总体的一个样本 B.2300名考生是总体
C.每位学生的数学成绩是个体 D.150名学生是样本容量
二、填空题
13.如图是根据我县教育局网站上公布的某初中为玉树地震灾区捐款的情况而制作的统计图,已知该校在校学生有人,请根据统计图计算该校共捐款 元.
14.为了调查夏季冷饮市场上的一批冰淇淋的质量情况,适宜的调查方式是 .
15.某校八年级200名学生参加生命安全知识测试,测试分数均大于或等于60且小于100,分数段的频率分布情况如表所示(其中每个分数段可包括最小值,不包括最大值),结合表的信息,可测得测试分数在分数段的学生有 名.
分数段
频率
16.某校为了解七年级学生对“七步洗手法”的掌握情况,现在800名七年级学生中随机抽取60名学生进行调查,则此次调查的样本容量是 .
17.老师随机抽查了本学期学生阅读课外书册数的情况,并将抽查结果绘制成条形图(图1)和不完整的扇形图(图2),其中条形图被墨迹遮盖了一部分.总人数为 ;扇形图中5册所占的圆心角的度数为 .
三、解答题
18.为了解某校中学生有多少人已患上近视眼,判断下列选取对象的方案是否恰当 不恰当的请说明理由.
(1)在学校门口数有多少人戴眼镜;
(2)在低年级的学生中随机抽取一个班作调查;
(3)从每个年级每个班级都随机抽取几个学生作调查.
19.判断下面这几个抽样调查选取样本的方法是否合适,并说明理由.
(1)为了解全班同学期末考试的平均成绩,老师抽查了前5名同学的平均成绩;
(2)教育部为了调查全国中小学乱收费情况,调查了某市所有中小学;
(3)某兴趣小组为了解本校1 800名学生的视力情况,随机抽查了本校九年级学生中50名学生的视力情况.
20.请指出下列抽样调查中的总体、个体、样本和样本容量
(1)为了解某所学校的学生参加课外体育活动的时间,调查了其中20名学生每天参加课外体育活动的时间;
(2)为了解某公园一年中平均每天进园的人数,对其中30天进园的人数进行了统计;
(3)为了解八年级学生的视力情况,学校从八年级随机抽取44名学生进行视力检查.
21.某校为了解落实“双减”政策后学生每天完成书面作业的时间t(单位:分钟)的情况,在全校随机抽取部分小学生进行调查,按四个组别进行整理,绘制成如下两幅不完整的统计图表,请根据图表信息解答下列问题:
抽取的学生作业时间统计表
组别 调查结果 人数(人)
A 120
B a
C 180
D 90
(1)这次调查抽取学生的总人数是_______,B组的学生人数______;
(2)该校共有学生1500人,请估算该校每日书面作业时间不少于90分钟的学生人数;
(3)请结合数据对该校“双减”工作提出一条合理性建议.
22.下列抽样调查中所选的样本合适吗?
(1)张老师为了解全班50名学生对英语单词的掌握情况,抽取5名学生进行检查;
(2)为了解全校26个班的课外活动情况,从七年级中抽取两个班进行分析;
(3)为调查全市中学生的上网情况,在全市的300所中学中随意抽取50所学校的学生进行调查;
(4)为了解我国中学多媒体的普及情况,在北京市做了抽样调查.
23.小丽同学本学期由于努力学习,数学成绩稳步提高.下表为小丽同学本学期近5次数学考试成绩:
第1次 第2次 第3次 第4次 第5次
成绩/分 80 85 85 90 90
(1)补全折线图:
(2)已知第6次数学考试的难度与前5次相当,根据上面数据,请你预测一下小丽第6次的数学考试成绩可能会是多少分,并说明你的理由(言之有理即可).
24.某校八年级有800名学生,从中随机抽取了名学生进行立定跳远测试,指出下列说法中哪些是正确的.
(1)这种调查方式是抽样调查.
(2)800名学生是总体.
(3)每名学生的立定跳远成绩是个体.
(4)这名学生的立定跳远成绩是总体的一个样本.
(5)名学生是样本容量.
《第七章数据的收集、整理与描述》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B B A B D B C C C
题号 11 12
答案 B C
1.C
【分析】本题考查了扇形统计图圆心角度数的算法,熟练掌握圆心角度数的算法是解决本题的关键.用乘以步行所占百分比即可.
【详解】解:由题意可得,步行所在的扇形圆心角的度数:
.
故选:C.
2.B
【分析】根据样本(被抽取的个体组成一个样本)、个体(组成总体的每一个考查对象)、总体(要考查的全体对象)、样本容量的定义(样本中个体的数目称为样本容量)逐项判断即可得.
【详解】解:A、抽取的100名学生的竞赛成绩是总体的一个样本,则此项错误,不符合题意;
B、每名学生的竞赛成绩是个体,则此项正确,符合题意;
C、全校2800名学生的竞赛成绩是总体,则此项错误,不符合题意;
D、样本容量是100,则此项错误,不符合题意;
故选:B.
【点睛】本题考查了样本、个体、总体、样本容量,熟记各概念是解题关键.
3.B
【分析】本题考查了全面调查与抽样调查,熟练掌握全面调查与抽样调查的特点是解题的关键.根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似判断即可.
【详解】解:A. 对搭乘高铁的乘客进行安全检查,适合全面调查,故A不符合题意;
B. 调查某市中学生的视力情况,适合抽样调查,故B符合题意;
C. 审核书稿中的错别字,适合全面调查,故C不符合题意;
D. 调查某班同学防溺水安全知识学习情况,适合全面调查,故D不符合题意;
故选:B.
4.A
【分析】本题考查了数据分组的方法,熟练掌握组数与极差和组距的关系是解题的关键.
求得最大值与最小值的差,除以组距就是组数.
【详解】(组)
故选:A
5.B
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
【详解】A、旅客上飞机前的安检,应该采用全面调查方式,不合题意;
B、了解某地区饮用水矿物质含量的情况,采用抽样调查方式,符合题意;
C、调查某种品牌笔芯的使用寿命,应该采用抽样调查方式,不合题意;
D、调查湖南卫视《会画少年的天空》节目的收视率,应该采用抽样调查方式,不合题意;
故选:B.
【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查,事关重大的调查往往选用普查.
6.D
【分析】本题考查的是全面调查和抽样调查,根据全面调查和抽样调查的概念判断即可.通过普查可以直接得到较为全面、可靠的信息,但花费的时间较长,耗费大,且一些调查项目并不适合普查.其一,调查者能力有限,不能进行普查.其二,调查过程带有破坏性.其三,有些被调查的对象无法进行普查.
【详解】解:A、查神舟十九号载人飞船的零部件是否符合标准,适合做全面调查,不符合题意;
B、调调查三位宇航员的身体状况,适合做全面调查,不符合题意;
C、调查宇航员的太空服是否符合安全标准,适合做全面调查,不符合题意;
D、调查神舟十九号载人飞船发射时的收视率,不适合做全面调查,符合题意.
故选:D.
7.B
【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
【详解】解:A.总体是该校4000名学生的体重,说法正确,故A不符合题意;
B.个体是每一个学生的体重,原来的说法错误,故B符合题意;
C.样本是抽取的400名学生的体重,说法正确,故C不符合题意;
D.样本容量是400,说法正确,故D不符合题意.
故选:B.
【点睛】本题主要考查了总体、个体、样本、样本容量,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
8.C
【分析】本题考查了两种统计图的认识,解题的关键是正确的利用这两种统计图的关系.
①用了解很少的学生数除以该组所占比例即可得到总人数; ②用学生总数乘以该组所占的比例得到基本了解的学生数;③扇形所对圆心角的度数等于圆周角乘以该组所占比例.
【详解】解:①∵了解很少的学生有25人,占学生总数的,
∴参加问卷调查的学生有人,故①正确;
②人,
∴参加进行问卷调查的学生中,“基本了解”的有15人,故②错误;
③,
∴“基本了解”部分的扇形的圆心角的度数是,故③正确;
“了解”的学生有,占比为,故④正确;
故选C.
9.C
【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目,据此逐项判断即可得出结论.
【详解】A、800名学生的身高是总体,故此选项错误,不符合题意;
B、每个学生的身高是个体,故此选项错误,不符合题意;
C、每个学生的身高是个体,故此选项正确,符合题意;
D、样本容量是,不带单位,故此选项错误,不符合题意;
故选:C.
【点睛】本题考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象,总体、个体与样本的考查对象是相同的,所不同的是范围的大小,样本容量是样本中包含的个体的数目,不能带单位.
10.C
【分析】对各种统计图优势的理解,根据题意选择合适的统计图即可.
【详解】扇形统计图能很好的表示部分与整体之间的关系.所以为直观地表示出各成分在总体中所占的百分比,最合适的统计图是扇形统计图.
故选:C
【点睛】本题考查对各种统计图优势的理解,根据题意选择合适的统计图即可.
11.B
【分析】利用数据统计表中对应的百分比计算即可.
【详解】解:
故选:B.
【点睛】本题考查数据统计中统计表,百分比的意义,理解百分比的意义是解题的关键.
12.C
【分析】总体是指考查对象的全体,个体是总体中的每一个考查对象.样本是指总体中所抽取的部分个体,样本容量是指样本中个体的数目,据此求解即可.
【详解】总体是我县初一2300名学生在疫情期间“数学空课”的学习情况 ;
样本是这150名考生在疫情期间“数学空课”的学习情况;
个体是每位学生的数学成绩;
样本容量是150.
故选:C.
【点睛】本题主要考查了总体、个体、样本和样本容量的定义,解题要分清具体问题中的总体、个体与样本的区别,关键是明确考查对象的范围.样本容量只是个数字,没有单位.
13.12590
【分析】根据扇形统计图中的数据求出各年级人数,再根据条形统计图中的数据求出各年级捐款数,各年级相加即可得到该校捐款总数.
【详解】解:1000×32%×15=4800元;
1000×33%×13=4290元;
1000×35%×10=3500元;
∴该校学生共捐款4800+4290+3500=12590元.
故答案为:12590.
【点睛】此题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
14.抽样调查
【分析】调查对象数量众多,可操作性低,耗时耗力的情况下,应采用抽样调查.
【详解】解:该冰淇淋可能销往世界各地,消费者众多,若采用全面调查不易操作,且耗时耗力;
故应采用抽样调查的方式.
故答案为:抽样调查
【点睛】本题考查抽样调查的适用特点.熟悉特点是解题关键.
15.60
【分析】先根据表格求出频率,再用总数乘以频率进行求解即可得到答案.
【详解】解:由表格可知,测试分数在分数段的学生的频率为,
所以,测试分数在分数段的学生人数为(名),
故答案为:60.
【点睛】本题考查了频数与频率,解题关键是掌握频率频数总数.
16.60
【分析】根据样本容量:“抽取的样本中的数量”,作答即可.注意样本容量不带单位.
【详解】解:由题意,此次调查的样本容量是60;
故答案为:60.
17. 24 135°/135度
【分析】由6册人数及其所占百分比求出总人数,再根据各册数的人数和等于总人数可得5册人数,用360°乘以对应人数所占比例即可得.
【详解】解:∵被调查的总人数为6÷25%=24(人),
∴5册的人数为24-(5+6+4)=9(人),
扇形图中5册所占的圆心角的度数为360°×=135°,
故答案为:24;135°.
【点睛】此题考查了条形统计图与扇形统计图的知识.注意掌握条形统计图与扇形统计图各量的对应关系是解此题的关键.
18.(1)不恰当,理由见解析
(2)不恰当,理由见解析
(3)恰当
【分析】根据选取的样本是否具有代表性依次判断即可求解.
【详解】(1)不恰当;因为可能有住校学生没调查到.
(2)不恰当;因为低年级学生的视力一般比高年级学生好.
(3)样本具有代表性,因此恰当.
【点睛】本题考查了样本的代表性,解题关键是掌握选取的样本应该具有代表性,要求学生能根据实际情况进行判断.
19.(1)不合适,理由见解析
(2)不合适,理由见解析
(3)不合适,理由见解析
【分析】本题考查了样本的选取,解题的关键是要考虑样本具有广泛性与代表性,所谓代表性,就是抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
(1)前5名同学成绩的平均数不能代表全班同学期末考试的平均成绩,不具有代表性,由此即可解答;
(2)某市所有中小学乱收费情况的数据不能代表全国中小学乱收费情况,不具有广泛性和代表性,由此即可解答;
(3)本校九年级学生中50名学生的视力情况不能代表本校1 800名学生的视力情况,不具有代表性,由此即可解答.
【详解】(1)不合适,前5名同学成绩的平均数会大于整个班级同学成绩的平均数,这样,样本就不具有代表性了.
(2)不合适,样本虽然足够大,但遗漏了其他地区的这些群体,应该在全国范围内选取样本.此外,将某市所有中小学乱收费情况作为样本是没有必要的.
(3)不合适,本校九年级学生视力情况的调查结果不能代表本校全部学生的视力情况,应该从全校各年级的学生中随机抽查.
20.(1)见解析
(2)见解析
(3)见解析
【分析】本题考查了总体、个体、样本、样本容量的知识,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
(1)根据总体、个体、样本、样本容量的定义,进行判断即可;
(2)根据总体、个体、样本、样本容量的定义,进行判断即可;
(3)根据总体、个体、样本、样本容量的定义,进行判断即可.
【详解】(1)解:总体:该校学生参加课外体育活动的时间;
个体:每位学生参加课外体育活动的时间;
样本:20名学生每天参加课外体育活动的时间;
样本容量:20;
(2)解:总体:该公园一年中平均每天进园的人数;
个体:每天进园的人数;
样本:其中30天进园的人数;
样本容量:30;
(3)解:总体:八年级学生的视力情况;
个体:每个学生的视力情况;
样本:44名学生的视力情况;
样本容量:44.
21.(1)600,210
(2)该校每日作业时长不少于90分钟的学生人数为675人
(3)建议该学校作业布置要减少题量或降低难度.(答案不唯一)
【分析】(1)根据总人数=A组人数÷A组所占百分比,总人数×B组百分比,即可求出本题答案;(2)1500×不低于90分钟学生的百分比,即可求出结果;(3)合理即可.
【详解】(1)这次调查抽取学生的总人数是600,B组的学生人数;
故答案为:600,210;
(2)(人),
答:该校每日作业时长不少于90分钟的学生人数为675人;
(3)该校每日作业时长不少于90分钟的学生人数占比高达45%,建议该学校作业布置要减少题量或降低难度.(答案不唯一,理由合理即可,没有结合数据得1分)
【点睛】本题考查统计表和扇形统计图,考查数据处理和分析的能力,解题关键在从不同的图中读出相应的统计量.
22.(1)不合适
(2)不合适
(3)合适
(4)不合适
【分析】根据抽取样本的方法进行判断即可:抽取样本时就是要考虑样本具有广泛性与代表性,所谓代表性,就是抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
【详解】(1)解:抽样较少,不能反映出全班学生对英语单词的掌握情况,所以所选样本不合适.
(2)解:从七年级抽取两个班不具有代表性,所以所选样本不合适.
(3)解:由于抽样是随机的,且数量适中,所以所选样本比较合适.
(4)解:抽取的样本具有片面性,不具有代表性,所以所选样本不合适.
【点睛】本题考查抽样调查的可靠性,样本具有代表性是指抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
23.(1)见解析
(2)95分,见解析
【分析】本题考查了折线统计图的作图,应用,熟练掌握统计图的意义是解题的关键.
(1)根据折线图画图方法,完善图即可.
(2)根据折线图的发展趋势,可以预测提升5分,解答即可.
【详解】(1)小丽同学本学期近5次数学考试成绩折线图如答图.
(2)解:预测小丽第6次的数学考试成绩为95分.
理由:由折线规律发现,小丽同学本学期近5次数学考试成绩稳步提升,第6次测验的难度与前5次相当,所以这次数学成绩可能提高5分,成绩为95分.
24.(1)正确
(2)错误
(3)正确
(4)正确
(5)错误
【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
【详解】(1)解:八年级有800名学生,从中随机抽取了100名学生进行立定跳远测试,是抽样调查,故(1)正确;
(2)800名学生的立定跳远成绩是总体,故(2)错误;
(3)每名学生的立定跳远成绩是个体,故(3)正确;
(4)这100名学生的立定跳远成绩是总体的一个样本,故(4)正确;
(5)100是样本容量,故(5)错误.
【点睛】本题考查了总体、个体、样本、样本容量、抽样调查与全面调查等概念,掌握这些概念是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
