8.3平行线的性质同步练习（含解析）

中小学教育资源及组卷应用平台
8.3平行线的性质
学校:___________姓名：___________班级：___________考号：___________
一、单选题
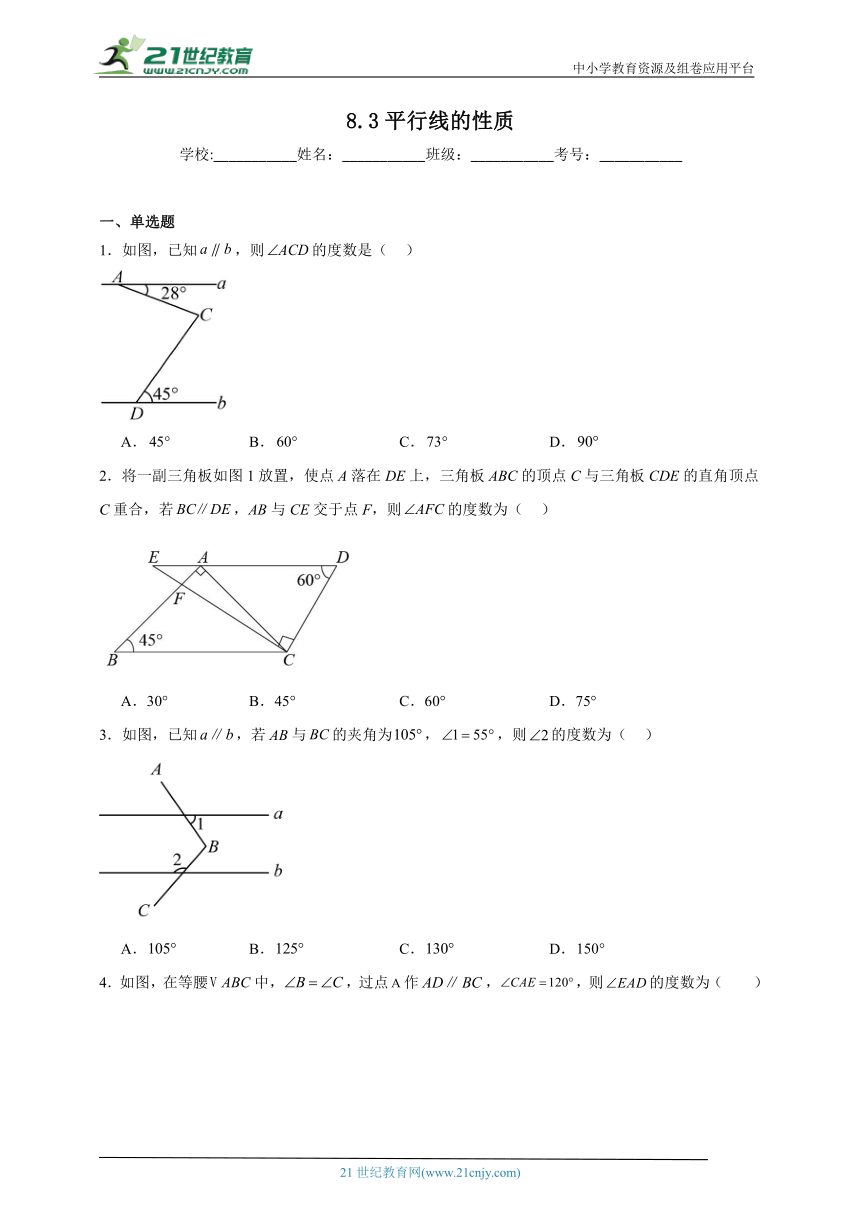
1．如图，已知，则的度数是（ ）
A． B． C． D．
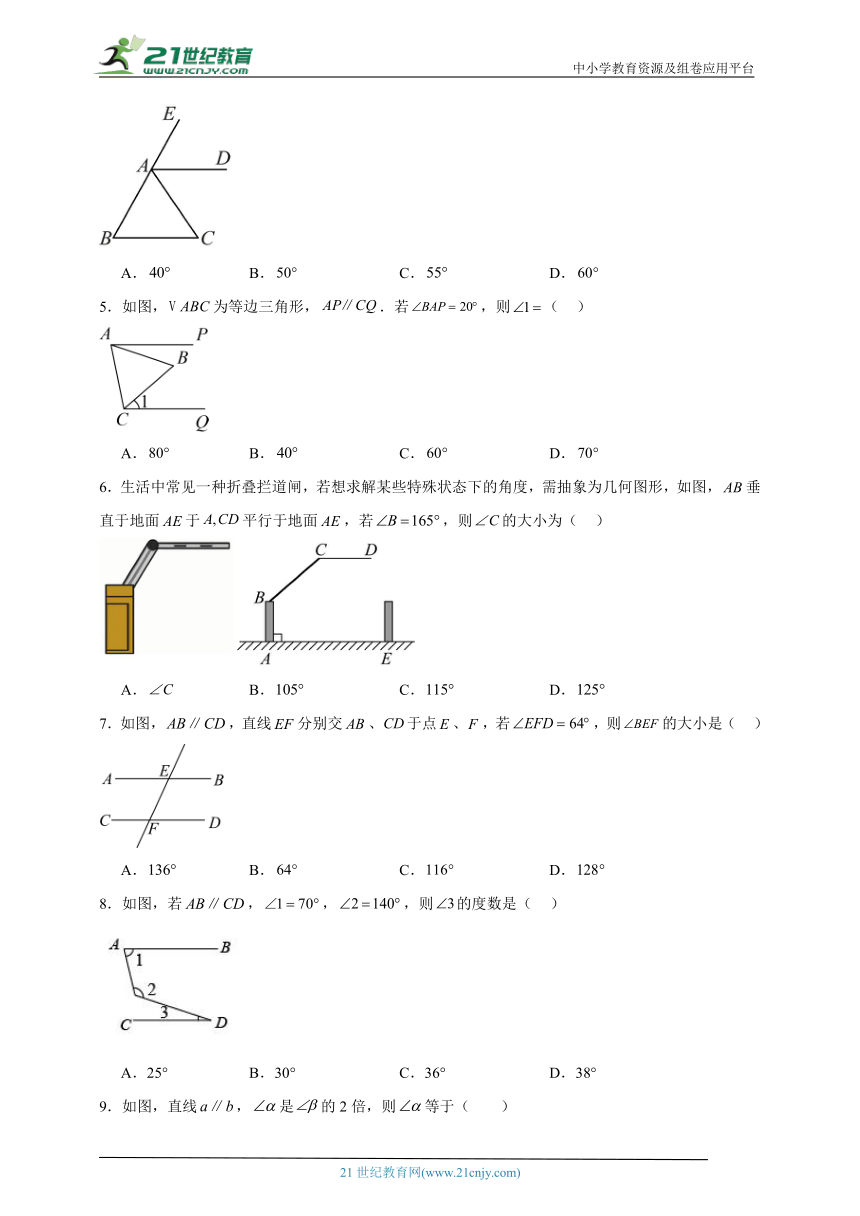
2．将一副三角板如图1放置，使点A落在DE上，三角板ABC的顶点C与三角板CDE的直角顶点C重合，若，AB与CE交于点F，则的度数为（ ）
A．30° B．45° C．60° D．75°
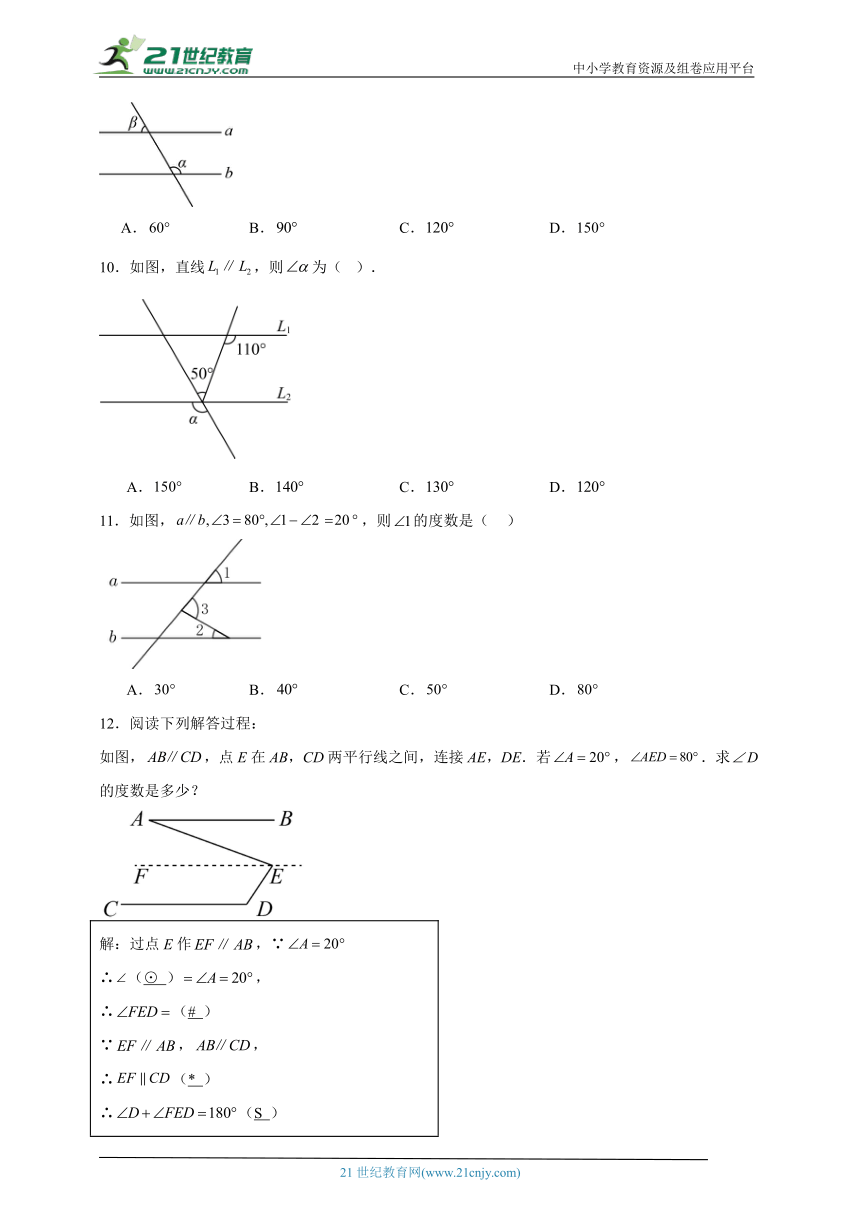
3．如图，已知，若与的夹角为，，则的度数为（ ）
A． B． C． D．
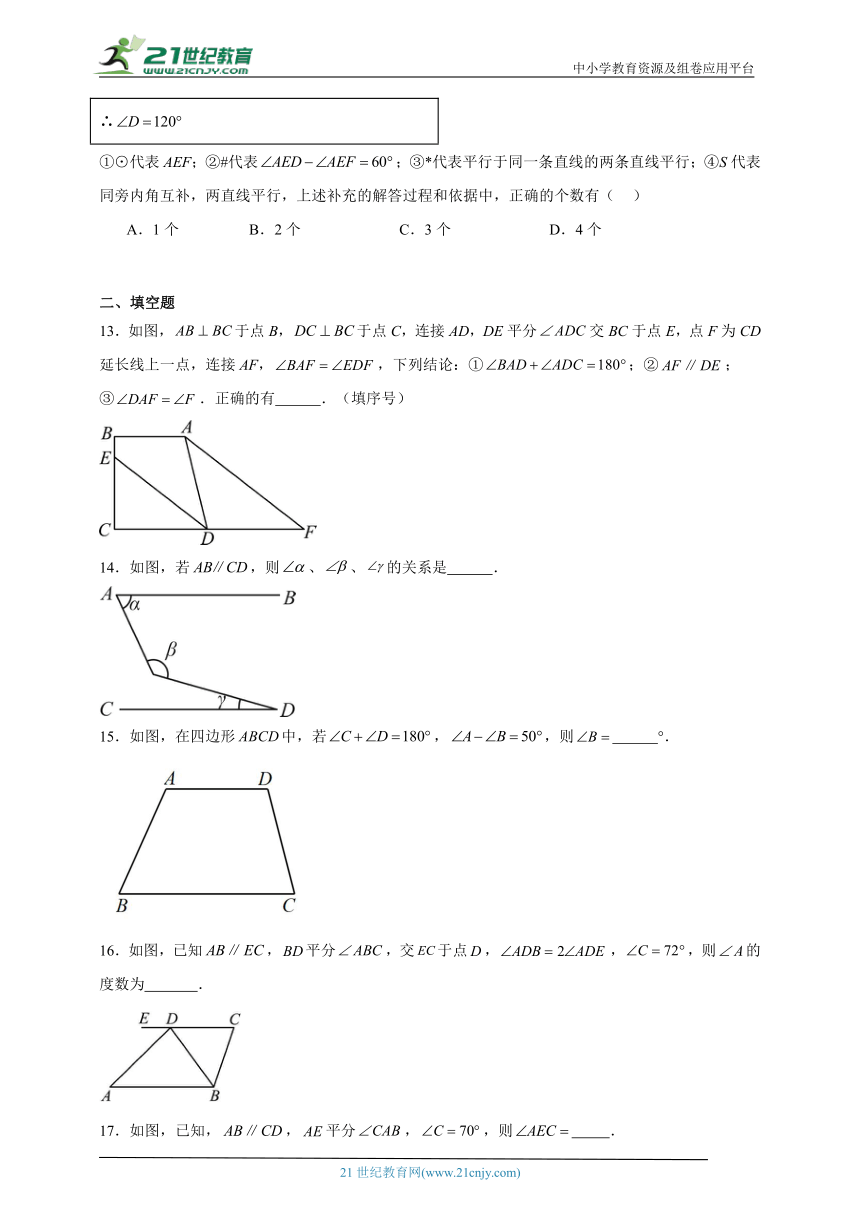
4．如图，在等腰中，，过点作，，则的度数为（　　）
A． B． C． D．
5．如图，为等边三角形，．若，则（ ）

A． B． C． D．
6．生活中常见一种折叠拦道闸，若想求解某些特殊状态下的角度，需抽象为几何图形，如图，垂直于地面于平行于地面，若，则的大小为（ ）
A． B． C． D．
7．如图，，直线分别交、于点、，若，则的大小是（ ）

A． B． C． D．
8．如图，若，，，则的度数是（ ）
A．25° B．30° C．36° D．38°
9．如图，直线，是的2倍，则等于（　　）
A． B． C． D．
10．如图，直线，则为（ ）．

A． B． C． D．
11．如图，，则的度数是（ ）
A． B． C． D．
12．阅读下列解答过程：
如图，，点E在AB，CD两平行线之间，连接AE，DE．若，．求的度数是多少？
解：过点E作，∵ ∴（⊙ ）， ∴（# ） ∵，， ∴（* ） ∴（S ） ∴
①⊙代表AEF；②#代表；③*代表平行于同一条直线的两条直线平行；④S代表同旁内角互补，两直线平行，上述补充的解答过程和依据中，正确的个数有（ ）
A．1个 B．2个 C．3个 D．4个
二、填空题
13．如图，于点B，于点C，连接AD，DE平分交BC于点E，点F为CD延长线上一点，连接AF，，下列结论：①；②；③．正确的有 ．（填序号）
14．如图，若，则、、的关系是 ．

15．如图，在四边形中，若，，则 °．

16．如图，已知，平分，交于点，，，则的度数为 ．
17．如图，已知，，平分，，则 ．

三、解答题
18．已知，点E在上，点F在DC上，点G为射线上一点．
(1)【基础问题】如图 1，试说明：．（完成图中的填空部分）证明：过点G作直线，
又∵，
∴ ①
∵，
∴∠ ② ．
∵，
∴ ③ （ ④ ）
∴．
(2)【类比探究】如图 2，当点G在线段延长线上时，请写出三者之间的数量关系，并说明理由．
(3)【应用拓展】如图 3，平分，交于点H，且，直接写出的度数为 °．
19．（1）问题发现：如图1，直线，连接，可以发现．
请把下面的解答过程补充完整：
解：过点作，
（_______________）．
（已知）
（_______________）．
．
_______________．
（等量代换）．
（2）拓展探究：如果点运动到图2所示的位置，其他条件不变，试说明：．

【拓展变式】如图，平分平分，则_______________．

20．如图，已知：点A在射线上，，，．

(1)求证：；
(2)猜测和的位置关系，说明理由．
21．如图，已知，．
(1)试说明；
(2)若，求的度数．
22．如图，直线，点在直线上，且，，求的度数．
23．如图，已知，数学课上，老师请同学们根据图形特征添加一个关于角的条件，使得，并给出证明过程．
小明添加的条件：．
请你帮小明将下面的说明过程补充完整．
解：∵（已知），
∴___________（___________）．
（___________）．
___________（___________）．
（___________）．
（___________）．
24．已知，点B、C在上（B在C左侧），A在上，连接,，，平分，平分交于点E．
(1)求的度数；
(2)若将图1中的线段沿向右平移到如图2所示位置．平分平分交于点E，，请你直接写出的度数；
(3)若将图1中的线段沿向左平移到如图3所示位置．其它条件与（2）相同．猜想此时的度数又是多少．（不需要证明）
《8.3平行线的性质》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C D B B C B C D
题号 11 12
答案 C C
1．C
【分析】如图，过点作直线，根据平行线的性质得到．
【详解】解：如图，过点作直线，则．
又，
，
，
．
故选：C．
【点睛】本题考查了平行线的性质．关键是熟悉两直线平行，内错角相等的知识点．
2．D
【分析】根据平行线的性质，三角形内角和定理求解即可．
【详解】解：由题意可知，∠E=30°，∠ACB=45°，∠FAC=90°，
∵
∴∠ECB=∠E=30°，
∴∠ACF=∠ACB-∠ECB=45°-30°=15°，
在△AFC中，∠AFC=180°-∠FAC-∠ACF=75°．
故选D
【点睛】本题考查平行线的性质，三角形内角和定理，根据图形灵活运用这些知识是解题的关键．
3．C
【分析】本题主要考查了平行线的性质及判定，掌握平行线的性质及判定是解本题的关键．
过点作，由可得，进而可得出，即可求解．
【详解】解：如图，过点作，
，
，
，，
，
，
．
故选：C
4．D
【分析】根据三角形外角的定义及性质可知，最后利用平行线的性质可知即可．
【详解】解： ∵在等腰中，，
∴在中，，
∵，
∴，
∴，
∵，
∴，
∴的度数为，
故选．
5．B
【分析】过点B作，可得，用平行线性质求解即可．
【详解】解：过点B作，如图，

∵，
∴，
∴，
∵为等边三角形，
∴，
∴，
∵，
∴，
故选：B．
【点睛】本题考查平行线的判定与性质，正确作出辅助线是关键．
6．B
【分析】过点B作，如图，由于垂直于地面，则，根据两直线平行，同旁内角互补得，由得，于是得到结论．本题主要考查了平行线的性质，正确作出辅助线，并熟记两直线平行，同旁内角互补是解决问题的关键．
【详解】解：∵垂直于地面，
∴，
过点B作，
∵平行于地面，
∴，
∴，
∴，
又∵，
∴，
故选B．
7．C
【分析】本题考查了平行线的性质，根据两直线平行，同旁内角互补求解即可．
【详解】解：∵，
∴，
∵，
∴，
故选：C．
8．B
【分析】延长AE交CD于点F，根据两直线平行，同旁内角互补，可得∠EFD，再根据三角形外角的性质即可求出∠3．
【详解】解：如图所示，延长AE交CD于点F，
∵，，
∴∠1+∠ACD=180°，
∴∠ACD=180°-∠1=180°-70°=110°，
∵∠2是△DEF的外角，
∴∠3+∠AFD=∠2，
∴∠3=∠2-∠AFD=140°-110°-30°．
故选：B
【点睛】本题考查平行线的性质，三角形外角的性质，熟练掌握平行线的性质，作出辅助线是解题的关键．
9．C
【分析】本题考查的是平行线的性质，对顶角的性质，先证明，可得，再进一步解答即可；
【详解】解：如图，∵，
∴．
又∵，
∴，
又∵是的2倍，
∴，
∴，
∴．
故选C
10．D
【分析】根据平行线的性质可求出，再根据对顶角的性质求出
【详解】解：如图，

∵，
∴
∴
由对顶角的性质可得
故选：D
【点睛】本题主要考查了平行线的性质和对顶角的性质，正确识别图形是解答本题的关键
11．C
【分析】根据平行线的性质和三角形外角的性质可得∠1＋∠2＝80°，结合，两式相加即可求出．
【详解】解：如图，∵，
∴∠4＝∠1，
∴∠3＝∠4＋∠2＝∠1＋∠2＝80°，
∵，
∴，
∴，
故选：C．
【点睛】本题考查了平行线的性质，三角形外角的性质，求出∠1＋∠2＝80°是解题的关键．
12．C
【分析】先根据平行线的性质可得，则，再根据平行于同一条直线的两条直线平行可得，然后根据平行线的性质即可得．
【详解】解：过点作，∵，
∴，
∴，
∵，，
∴（平行于同一条直线的两条直线平行），
∴（两直线平行，同旁内角互补），
∴．
由此可知，⊙代表，则①正确；
#代表，则②正确；
*代表平行于同一条直线的两条直线平行，则③正确；
代表两直线平行，同旁内角互补，则④错误；
综上，正确的个数有3个，
故选：C．
【点睛】本题考查了平行线的性质、平行公理推论，熟练掌握平行线的性质是解题关键．
13．①②③
【分析】①证明AB∥CD，可做判断；②根据平行线的判定和性质可做判断；③根据AF∥ED得内错角相等和同位角相等，再由角平分线的定义得∠ADE=∠CDE，从而可做判断．
【详解】解：①∵AB⊥BC，DC⊥BC，
∴AB∥CD，
∴∠BAD+∠ADC=180°，故①正确；
②∵AB∥CD，
∴∠AFD+∠BAF=180°，
∵∠BAF=∠EDF，
∴∠AFD+∠EDF=180°，
∴AF∥DE，故②正确；
③∵AF∥ED，
∴∠DAF=∠ADE，∠F=∠CDE，
∵DE平分∠ADC，
∴∠ADE=∠CDE，
∴∠DAF=∠F，故③正确；
故答案为：①②③．
【点睛】本题主要考查了平行线的判定与性质，平行线的判定是由角的数量关系判断两直线的位置关系，平行线的性质是由平行关系来寻找角的数量关系．
14．
【分析】过点E作，则，根据平行线的性质计算求解即可．
【详解】解：如图，过点E作，

∵，
∴，
∴，，
∵，
∴，
∴，
故答案为：．
【点睛】本题考查了平行线的判定和性质，熟练掌握判定和性质是解题的关键．
15．/65度
【分析】先根据判定出，再根据两直线平行，同旁内角互补得到，然后联立求解即可.
【详解】解：∵，
∴，
∴，
又∵，
∴，，
故答案为：.
【点睛】本题考查了平行线的判定与性质，先判定出是解题的关键，也是解题的突破口.
16．
【分析】本题考查平行线的性质，角度的和差，角平分线，熟练掌握平行线的性质是解题的关键．利用，得出，，，则可求出，利用平分，求出，则可得，利用，可求出，即可求解．
【详解】解：∵，
∴，，，
∵，
∴，
∵平分，
∴，
∴，
∴，
∵，
∴，
∴，
故答案为：．
17．
【分析】根据平行线性质求出，根据角平分线求出，根据平行线性质求出即可．
【详解】解：，
，，
，
，
平分，
，
．
故答案为：．
【点睛】本题考查平行线的性质，角平分线的定义等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
18．(1)；；；两直线平行，内错角相等
(2)．理由见解析
(3)
【分析】（1）由，可得，由，可得，则；
（2）如图所示，过点G作直线，同理可得，，则．
（3）如图所示，过点G作直线，过点H作直线，得到，由，得到，再由，可得，再由平分，即可得到，则．
【详解】（1）过点G作直线，
又∵，
∴（平行于同一条直线的两条直线平行），
∵，
∴（两直线平行，内错角相等），
∵，
∴（两直线平行，内错角相等），
∴．
故答案为：；；；两直线平行，内错角相等．
（2）如图所示，过点G作直线，
又∵，
∴，
∵，
∴，
∵，
∴，
∴．
（3）如图所示，过点G作直线，过点H作直线，
又∵，
∴，
∵，，
∴，
∵，，
∴，
∵，
∴，
∴，
∴，
∵平分，
∴，
∴，
∴．
【点睛】本题主要考查了平行线的性质，平行公理，解题的关键在于能够熟练掌握平行线的性质．
19．（1）两直线平行，内错角相等；平行于同一条直线的两条直线平行；；（2）见解析；【拓展变式】．
【分析】过点作，根据两直线平行，内错角相等进行推理解题即可；
（2）过点作，根据两直线平行，同旁内角互补推理解题即可；【拓展变式】利用和（2）的结论和角平分线的定义解题计算．
【详解】解：过点作，
（两直线平行，内错角相等）．
（已知）
（平行于同一条直线的两条直线平行）．
．
．
（等量代换）．
故答案为：两直线平行，内错角相等； 平行于同一条直线的两条直线平行；； （2）解：过点作（点在点左侧），
．
又，．
．
．
．
【拓展变式】解：由可知：
∵平分平分
∴，，
∴，
再由（2）可得，
∴，

故答案为：．
【点睛】本题考查平行线的性质，掌握过折点作平行线，构造内错角相等或同旁内角互补是解题的关键．
20．(1)见解析
(2)，理由见解析
【分析】（1）根据，得出，得出结论即可；
（2）先证明，再证明，由于，所以可得出和的位置关系.
【详解】（1）证明：∵，
∴，
∴；
（2）解：；
理由：∵，
∴；
∴，
又∵，
∴，
∴，
又∵，
∴．
【点睛】本题主要考查平行线的性质和判定，属于基础题，要灵活运用.
21．(1)见解析
(2)
【分析】（1）根据平行线的性质与等量代换可得，进而根据平行线的判定定理可得，根据平行线的性质即可得证；
（2）根据平行线的性质可得，即可求解．
【详解】（1），
，
又，
，
，
；
（2），
，
．
【点睛】本题考查了平行线的性质与判定，掌握平行线的性质与判定是解题的关键．
22．
【分析】根据平行线的性质可知，结合，即可求出的度数．
【详解】解：∵直线，
∴，
∵，
∴，
∵，
∴，
∵点在直线上，
∴，
∴．
【点睛】本题考查了平行线的性质、垂直的定义和平角的概念，熟知两直线平行，同位角相等是解答本题的关键．
23．，两直线平行，同位角相等；已知，，同位角相等，两直线平行；两直线平行，内错角相等；等式的基本事实
【分析】此题考查了平行线的判定和性质，根据得到，证明，得到，即可得到结论．
【详解】解：∵（已知），
∴（两直线平行，同位角相等）．
（已知）．
（同位角相等，两直线平行）．
（两直线平行，内错角相等）．
（等式的基本事实）．
故答案为：，两直线平行，同位角相等；已知，，同位角相等，两直线平行；两直线平行，内错角相等；等式的基本事实
24．(1)
(2)
(3)
【分析】（1）根据平行线的性质求出每个角的度数，然后利用三角形的内角和直接求解即可．
（2）作出辅助线，直接通过平行线的性质求解即可．
（3）作出平行的辅助线，直接通过平行线的性质和判定求解即可．
【详解】（1）∵，
∴，
∵，
∴，
∵分别平分，
∴，
∴，
∴．
（2）如图2中，延长交于点H．
由（1）可知， ，
∵，
∴，
∴，
∴；
（3）如图3中，过点E作．
∵，
∴，
∴，
∴，
∵，
∴，
∵平分，
∴，
∴．
【点睛】此题考查平行线的性质与判定，解题关键是灵活作出不同的辅助线，利用平行线的性质求出角度的数量关系．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)