9.3二元一次方程组与实际问题同步练习(含解析)
文档属性
| 名称 | 9.3二元一次方程组与实际问题同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 660.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 15:24:13 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
9.3二元一次方程组与实际问题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.“洛书”是世界上最古老的一个三阶幻方,它有3行3列,三横行的三个数之和,三竖列的三个数之和,两对角线的三个数之和都相等,其实幻方就是把一些有规律的数填在正方形图内,使每一行、每一列和每一条对角线上各个数之和都相等,如图幻方a、b的值分别是( )
A.11,9 B.9,11 C.8,13 D.13,8
2.鸡兔同笼,从上面数,有20个头;从下面数,有60条腿,设鸡有x只,兔有y只,则下列方程组正确的是( )
A. B.
C. D.
3.某公司有新员工和老员工若干名.已知1名新员工每天制造的零件个数比1名老员工少30,1名新员工与2名老员工每天共可制造180个零件,则1名新员工与1名老员工每天各能制造多少个零件?设1名新员工每天能制造个零件,1名老员工每天能制造个零件.根据题意可列方程组为()
A. B. C. D.
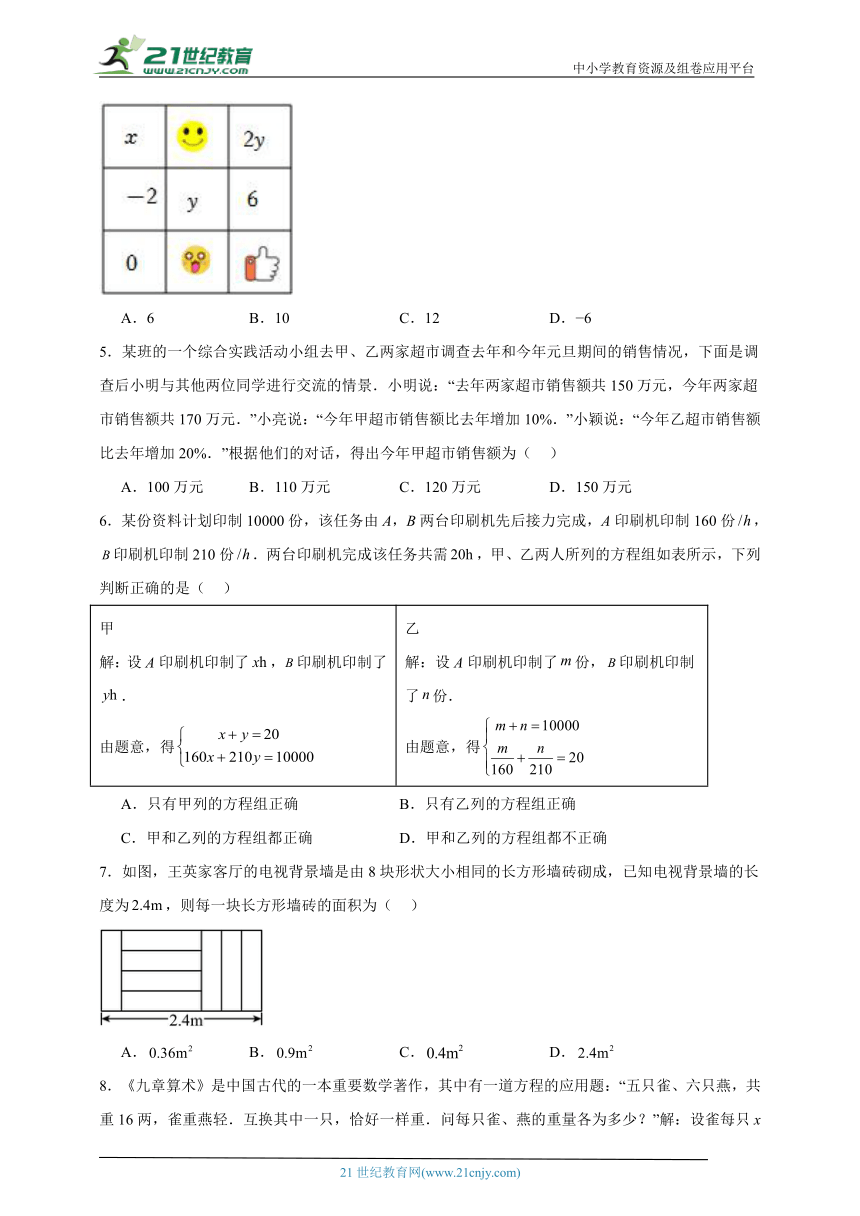
4.综合实践课上,同学们在如图所示的三阶幻方中,填写了一些数、式子和图案(其中每个式子或图案都表示一个数),若处于每一横行、每一竖列、两条斜对角线上的3个数之和都相等,则x+y的值为( )
A.6 B.10 C.12 D. 6
5.某班的一个综合实践活动小组去甲、乙两家超市调查去年和今年元旦期间的销售情况,下面是调查后小明与其他两位同学进行交流的情景.小明说:“去年两家超市销售额共150万元,今年两家超市销售额共170万元.”小亮说:“今年甲超市销售额比去年增加10%.”小颖说:“今年乙超市销售额比去年增加20%.”根据他们的对话,得出今年甲超市销售额为( )
A.100万元 B.110万元 C.120万元 D.150万元
6.某份资料计划印制10000份,该任务由A,B两台印刷机先后接力完成,A印刷机印制160份,印刷机印制210份.两台印刷机完成该任务共需,甲、乙两人所列的方程组如表所示,下列判断正确的是( )
甲 解:设A印刷机印制了,印刷机印制了. 由题意,得 乙 解:设A印刷机印制了份,印刷机印制了份. 由题意,得
A.只有甲列的方程组正确 B.只有乙列的方程组正确
C.甲和乙列的方程组都正确 D.甲和乙列的方程组都不正确
7.如图,王英家客厅的电视背景墙是由8块形状大小相同的长方形墙砖砌成,已知电视背景墙的长度为,则每一块长方形墙砖的面积为( )
A. B. C. D.
8.《九章算术》是中国古代的一本重要数学著作,其中有一道方程的应用题:“五只雀、六只燕,共重16两,雀重燕轻.互换其中一只,恰好一样重.问每只雀、燕的重量各为多少?”解:设雀每只x两,燕每只y两,则可列出方程组为( )
A. B.
C. D.
9.一个两位数的十位数字与个位数字的和是8,把这个两位数加上18,结果恰好成为数字对调后组成的两位数,求这个两位数.设个位数字为,十位数字为,所列方程组正确的是( )
A. B.
C. D.
10.幻方历史悠久,传说最早出现在夏禹时代的“洛书”.洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图1),将9个数填在的方格中,如果满足每行、每列,每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方.图2的主格中填写了一些数字和字母,若能构成一个广义的三阶幻方,则的值为( )
A.0 B.1 C.3 D.6
11.某市出租车起步价所包含的路程为,超过的部分按每千米另收费.明明乘坐这种出租车走了,付了16元;盼盼乘坐这种出租车走了,付了28元.设这种出租车的起步价为元,超过后每千米收费元,则下列方程正确的是( )
A. B.
C. D.
12.“方程”二字最早见于我国《九章算术》这部经典著作中,该书的第八章名为“方程”如:从左到右列出的算筹数分别表示方程中未知数x,y的系数与相应的常数项,即可表示方程,则表示的方程是( )
A. B. C. D.
二、填空题
13.如图宽为的长方形图案是用8块相同的小长方形地砖拼成的,则每块小长方形地砖的长是
14.某车间有90名工人,每人每天平均能生产螺栓15个或螺帽24个,要使一个螺栓配套两个螺帽,应该如何分配工人才能便生产的螺栓和螺帽刚好配套?若设生产螺栓人,生产螺帽人,则列方程组得 .
15.甲、乙两种商品原来的单价之和为元,因市场变化,甲商品降价,乙商品提价,调价后两种商品的单价的和为元,甲、乙两种商品原来的单价相差 元.
16.《九章算术》中记载:“今有共买羊,人出五,不足四十五;人出七,不足三.问人数、羊价各几何?”其大意是:今有人合伙买羊,若每人出五钱,还差45钱;若每人出七钱,还差3钱.问合伙人数是多少?此问题中合伙人数为 .
17.我国古代数学名著《九章算术》中记载:今有甲乙两人持钱不知其数,甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?意思是现有甲乙两人,都不知道有多少钱,若乙把他一半的钱给甲,则甲有钱;而甲把他的钱给乙,则乙有50钱,问甲、乙各有多少钱?如果设甲原来有x钱,乙原来有y钱,则可列方程组为 .
三、解答题
18.某中学组织学生春游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满,已知45座客车每日每辆租金为220元,60座客车每日每辆租金为300元.试问:
(1)春游学生共多少人?原计划45座客车多少辆?
(2)若租用同一种车,要使每位同学都有座位,应该怎样租用才合算?
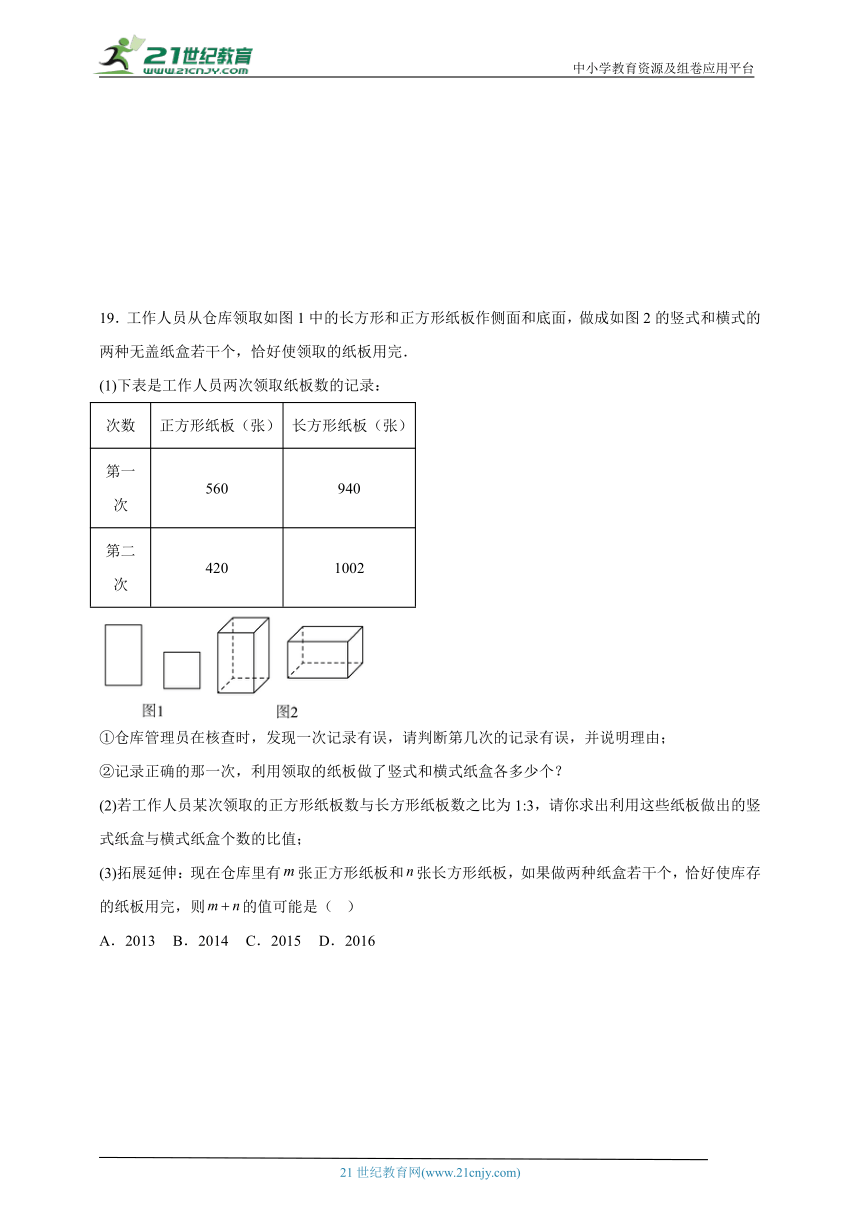
19.工作人员从仓库领取如图1中的长方形和正方形纸板作侧面和底面,做成如图2的竖式和横式的两种无盖纸盒若干个,恰好使领取的纸板用完.
(1)下表是工作人员两次领取纸板数的记录:
次数 正方形纸板(张) 长方形纸板(张)
第一次 560 940
第二次 420 1002
①仓库管理员在核查时,发现一次记录有误,请判断第几次的记录有误,并说明理由;
②记录正确的那一次,利用领取的纸板做了竖式和横式纸盒各多少个?
(2)若工作人员某次领取的正方形纸板数与长方形纸板数之比为1:3,请你求出利用这些纸板做出的竖式纸盒与横式纸盒个数的比值;
(3)拓展延伸:现在仓库里有张正方形纸板和张长方形纸板,如果做两种纸盒若干个,恰好使库存的纸板用完,则的值可能是( )
A.2013 B.2014 C.2015 D.2016
20.娄底市出租车收费规定:起步价所包含的路程为0~1.5千米,超过1.5千米的部分按每千米另收费.
刘同学说:“我乘出租车从市政府到娄底汽车站走了4.5千米,付车费11元.”
李同学说:“我乘出租车从市政府到娄底火车站走了6.5千米,付车费15元.”
问:
(1)出租车的起步价是多少元?超过1.5千米后每千米收费多少元?
(2)小张乘出租车从家里到娄底南站(高铁站)走了9.5千米,应付车费多少元?
21.某班决定购买两种绿植,已知购买A种绿植3盆和B种绿植4盆共需52元,购买A种绿植6盆和B种绿植5盆共需83元,问A种绿植和B种绿植每盆各多少元?
22.为迎接中考,很多同学购买了铅笔和涂卡尺.根据图中信息,求每支铅笔和每个涂卡尺的价格.
23.学校组织学生乘汽车去自然保护区野营,前路段为平路,其余路段为坡路.已知汽车在平路上行驶的速度为,在坡路上行驶的速度为.汽车从学校到自然保护区一共行驶了,求汽车在平路和坡路上各行驶了多长时间.
24.《张丘建算经》由北魏数学家张丘建所著,其中有这样一个问题:“今有客不知其数.两人共盘,少两盘;三人共盘,长三盘.问客及盘各几何?”意思为:“现有若干名客人.若2个人共用1个盘子,则少2个盘子;若3个人共用1个盘子,则多出来3个盘子.问客人和盘子各有多少?”请你解答这个问题.
《9.3二元一次方程组与实际问题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B A B B C A B B B
题号 11 12
答案 D A
1.D
【分析】本题是一道有关探究规律的题目,侧重考查知识点的应用能力,依题意,得,再解二元一次方程组即可.
【详解】解:依题意,得,
解得:,
故选:D.
2.B
【分析】根据鸡有两条腿,兔子有四条腿,共有20个头,60条腿,列出二元一次方程组即可.
【详解】解:由题意得:,
故选:B
【点睛】本题考查由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
3.A
【分析】本题二元一次方程组的应用,解题的关键是能够根据题意找到两个等量关系,这是列方程的依据.
找到两个等量关系列出方程组即可.
【详解】解:设一个生手工每天能制作x个零件,一个熟手工每天能制造y个零件,
根据题意得:,
故选A.
4.B
【分析】根据题意列出方程求出,的值,代入代数式求值即可.
【详解】解:根据题意得:,
解得:,,
.
故选:B.
【点睛】本题考查了有理数的加法,体现了方程思想,根据题意列出方程是解题的关键.
5.B
【解析】略
6.C
【分析】根据两台印刷机完成该任务共需和资料计划印制10000份,即可列出二元一次方程组.
【详解】解:∵两台印刷机完成该任务共需,
∴可列方程;
∵资料计划印制10000份,
∴可列方程,
∴甲和乙列的方程组都正确,
故选:C.
【点睛】本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
7.A
【分析】此题考查了二元一次方程组的实际应用,长方形的性质,根据长方形的两组对边分别相等列出方程组是解题的关键.
设一块长方形墙砖的长为,宽为,然后用的代数式分别表示出长方形的长为,两条宽分别为,,进而根据长方形的性质列出方程组,解方程组得到的值,再根据长方形面积计算公式即可求出面积,
【详解】解:设一块长方形墙砖的长为,宽为,依题意得,
,
解得,
∴每一块长方形墙砖的面积为:
答:每一块长方形墙砖的面积为.
故选:A.
8.B
【分析】本题考查的是二元一次方程组的应用,设雀每只两,燕每只两,根据“五只雀、六只燕,共重两,雀重燕轻.互换其中一只,恰好一样重”可列出方程组,从而可得答案.
【详解】解:设雀每只两,燕每只两,则可列出方程组为:
.
故选:B.
9.B
【分析】设个位数字为,十位数字为,根据“一个两位数的十位数字与个位数字的和是8”和“把这个两位数加上18,结果恰好成为数字对调后组成的两位数”列出方程组即可.
【详解】解:设个位数字为,十位数字为,
由题意得,,
故选:B
【点睛】此题考查了二元一次方程组的应用,读懂题意,找到两个等量关系是解题的关键.
10.B
【分析】根据三阶幻方中的数字列方程求解即可.
【详解】解:由题意,可得,
解得,
∴.
故选:B.
【点睛】本题主要考查二元一次方程组的应用以及零指数幂,熟练根据三阶幻方列方程求解是解题的关键.
11.D
【分析】本题主要考查由实际问题抽象出二元一次方程组.设这种出租车的起步价为x元,超过后每千米收费y元,根据题意列出二元一次方程组,即可求解.
【详解】解:设这种出租车的起步价为x元,超过后每千米收费y元,根据题意得,
,
故选:D.
12.A
【分析】本题考查了列二元一次方程,理解题意是解题的关键.根据横着的算筹为10,竖放的算筹为1,结合未知数的系数与等式后面的数字,即可求解.
【详解】
解:表示的方程是:
故选:A.
13.
【分析】首先设每块长方形的长是,宽是,然后根据图示列出关于x和y的二元一次方程组,从而求出x和y的值.
【详解】解:设每块长方形的长是,宽是,根据题意可得:
解得:
所以,长是,宽是.
故为答案:.
【点睛】此题考查方程组的应用问题,解题的关键是弄清题意,看懂图示,找出合适的等量关系,列出方程组,并弄清小长方形的长与宽的关系.
14.
【分析】根据某车间有90名工人,一个螺栓配套两个螺帽,列二元一次方程组即可.
【详解】解:根据题意,得,
故答案为: .
【点睛】本题考查了由实际问题抽象出二元一次方程组,理解题意并根据题意建立等量关系是解题的关键.
15.
【分析】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解答本题的关键.
设甲商品原来的单价为元,乙商品原来的单价为元,根据“甲、乙两种商品原来的单价之和为元,调价后两种商品的单价的和为元”,即可得出关于、的二元一次方程组,解之即可得出、的值,再将其代入中即可求出结论.
【详解】解:设甲商品原来的单价为元,乙商品原来的单价为元,
根据题意得,
解得,
,
故答案为:.
16.21
【分析】本题主要考查了二元一次方程组的应用.设合伙人数是x人,羊价为y元,根据“若每人出五钱,还差45钱;若每人出七钱,还差3钱.”列出方程组,即可求解.
【详解】解:设合伙人数是x人,羊价为y元,根据题意得:
,
解得:,
答:合伙人数是21人.
故答案为:21.
17.
【分析】本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.根据“若乙把他一半的钱给甲,则甲有钱”,“甲把他的钱给乙,则乙有钱” 即得出关于的二元一次方程组,即可求解.
【详解】解:由乙把他一半的钱给甲,则甲有钱,得
,
由甲把他的钱给乙,则乙有钱,得
,
可列方程组为.
故答案为:.
18.(1)七年级共有240人,计划租45座客车5辆
(2)租4辆60座更合算
【分析】(1)设七年级人数是x人,原计划租45座客车y辆,根据租用45座客车若干辆,但有15人没有座位,用同样数量的60座客车,则多出一辆车列出方程组,解方程组即可;
(2)分别算出租用同一种车时,需要的费用,然后进行比较即可.
【详解】(1)解:设七年级人数是x人,原计划租45座客车y辆,
由题意得:,
解得:
所以七年级共有240人,计划租45座客车5辆;
(2)解:只租45座需:
(元),
只租60座需: (元),
,
∴租4辆60座更合算.
【点睛】本题主要考查了二元一次方程的应用,解题的关键是根据等量关系,列出方程.
19.(1)①第二次,见解析;②做成40个竖式纸盒,260个横式纸盒
(2)3
(3)C
【分析】本题考查了二元一次方程组的应用,理解题意,找到正确的数量关系是本题的关键.
(1)①设做成x个竖式纸盒,y个横式纸盒,由领取的正方形的纸板和长方形的纸板之和应该是5的倍数,可判断第二次记录错误;
②由第一次记录,列出方程组,可求解;
(2)由正方形纸板数与长方形纸板数之比为1:3,可得,可求解;
(3)设做竖式和横式的两种无盖纸盒分别为x个、y个,然后根据所需长方形纸板和正方形纸板的张数列出方程组,再根据x、y的系数表示出并判断为5的倍数,然后选择答案即可.
【详解】(1)解:①第二次记录错误,
理由如下:设做成x个竖式纸盒,y个横式纸盒,
则需要正方形纸板张,需要长方形的纸板张,
∴领取的正方形的纸板和长方形的纸板之和为,应该是5的倍数,
而,,1422不能被5整除,
∴第二次记录有误;
②由题意可得:,
解得:,
答:做成40个竖式纸盒,260个横式纸盒;
(2)解:由题意可得:,
解得:,
∴,
答:竖式纸盒与横式纸盒个数的比值为3.
(3)解:设做竖式和横式的两种无盖纸盒分别为x个、y个,
根据题意得:,
两式相加得,,
∵x、y都是正整数,
∴是5的倍数,
∵2013、2014、2015、2016四个数中只有2015是5的倍数,
∴的值可能是2015.
故选:C.
20.(1)出租车的起步价是5元,超过1.5千米后每千米收费2元
(2)21元
【分析】(1)先设未知数,设出租车的起步价是x元,超过1.5千米后每千米收费y元.根据他们的对话建立2个等量关系,因为4.5千米和6.5千米都分两段收费,一段是1.5千米部分,一段是多于1.5千米的部分,再根据两段的单价和两人的付车费列出二元一次方程组求解;
(2)千米分两段收费:即1.5千米(起步价)+千米×单价=付车费.把(1)中的单价代入进行计算即可;
【详解】(1)解:设出租车的起步价是元,超过1.5千米后每千米收费元,
根据题意可得:,
即:,
解这个方程组,得:,
答:出租车的起步价是5元,超过1.5千米后每千米收费2元;
(2)小张应付的车费:(元),
答:小张应付的车费为21元.
【点睛】本题考查用二元一次方程组解决实际问题,解题关键弄清题中的等量关系.
21.A种绿植每盆8元,B种绿植每盆7元.
【分析】设A种绿植和B种绿植每盆x元和y元,根据“购买A种绿植3盆和B种绿植4盆共需52元,购买A种绿植6盆和B种绿植5盆共需83元”列方程组求解即可
【详解】解:设A种绿植和B种绿植每盆x元和y元,依题意,得
,
解方程得:
,
答:A种绿植每盆8元,B种绿植每盆7元.
【点睛】本题考查了二元一次方程组的应用,解题的关键是找准等量关系,正确的列出二元一次方程组.
22.每支2B铅笔和每个涂卡尺的价格分别为0.8元和1.5元
【分析】本题主要考查二元一次方程组的应用;设每支2B铅笔和每个涂卡尺的价格分别为元,元,根据题意,列出二元一次方程组,计算求解即可.
【详解】解:设每支2B铅笔和每个涂卡尺的价格分别为元,元,根据题意,
得
解得
答:每支2B铅笔和每个涂卡尺的价格分别为0.8元和1.5元.
23.汽车在平路上行驶了,在坡路上行驶了
【分析】本题考查的是二元一次方程组的应用,设汽车在平路上行驶了,在坡路上行驶了,再利用汽车从学校到自然保护区一共行驶了,前路段为平路,建立方程组求解即可.
【详解】解:设汽车在平路上行驶了,在坡路上行驶了,
由题意,得,
解得
答:汽车在平路上行驶了,在坡路上行驶了.
24.个客人,个盘子
【分析】本题考查二元一次方程,设有个客人,个盘子,根据题意列二元一次方程组并求解,找到正确的等量关系是解题的关键.
【详解】解:设有个客人,个盘子.
根据题意,得 ,
解得 ,
答∶有个客人,个盘子.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
9.3二元一次方程组与实际问题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.“洛书”是世界上最古老的一个三阶幻方,它有3行3列,三横行的三个数之和,三竖列的三个数之和,两对角线的三个数之和都相等,其实幻方就是把一些有规律的数填在正方形图内,使每一行、每一列和每一条对角线上各个数之和都相等,如图幻方a、b的值分别是( )
A.11,9 B.9,11 C.8,13 D.13,8
2.鸡兔同笼,从上面数,有20个头;从下面数,有60条腿,设鸡有x只,兔有y只,则下列方程组正确的是( )
A. B.
C. D.
3.某公司有新员工和老员工若干名.已知1名新员工每天制造的零件个数比1名老员工少30,1名新员工与2名老员工每天共可制造180个零件,则1名新员工与1名老员工每天各能制造多少个零件?设1名新员工每天能制造个零件,1名老员工每天能制造个零件.根据题意可列方程组为()
A. B. C. D.
4.综合实践课上,同学们在如图所示的三阶幻方中,填写了一些数、式子和图案(其中每个式子或图案都表示一个数),若处于每一横行、每一竖列、两条斜对角线上的3个数之和都相等,则x+y的值为( )
A.6 B.10 C.12 D. 6
5.某班的一个综合实践活动小组去甲、乙两家超市调查去年和今年元旦期间的销售情况,下面是调查后小明与其他两位同学进行交流的情景.小明说:“去年两家超市销售额共150万元,今年两家超市销售额共170万元.”小亮说:“今年甲超市销售额比去年增加10%.”小颖说:“今年乙超市销售额比去年增加20%.”根据他们的对话,得出今年甲超市销售额为( )
A.100万元 B.110万元 C.120万元 D.150万元
6.某份资料计划印制10000份,该任务由A,B两台印刷机先后接力完成,A印刷机印制160份,印刷机印制210份.两台印刷机完成该任务共需,甲、乙两人所列的方程组如表所示,下列判断正确的是( )
甲 解:设A印刷机印制了,印刷机印制了. 由题意,得 乙 解:设A印刷机印制了份,印刷机印制了份. 由题意,得
A.只有甲列的方程组正确 B.只有乙列的方程组正确
C.甲和乙列的方程组都正确 D.甲和乙列的方程组都不正确
7.如图,王英家客厅的电视背景墙是由8块形状大小相同的长方形墙砖砌成,已知电视背景墙的长度为,则每一块长方形墙砖的面积为( )
A. B. C. D.
8.《九章算术》是中国古代的一本重要数学著作,其中有一道方程的应用题:“五只雀、六只燕,共重16两,雀重燕轻.互换其中一只,恰好一样重.问每只雀、燕的重量各为多少?”解:设雀每只x两,燕每只y两,则可列出方程组为( )
A. B.
C. D.
9.一个两位数的十位数字与个位数字的和是8,把这个两位数加上18,结果恰好成为数字对调后组成的两位数,求这个两位数.设个位数字为,十位数字为,所列方程组正确的是( )
A. B.
C. D.
10.幻方历史悠久,传说最早出现在夏禹时代的“洛书”.洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图1),将9个数填在的方格中,如果满足每行、每列,每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方.图2的主格中填写了一些数字和字母,若能构成一个广义的三阶幻方,则的值为( )
A.0 B.1 C.3 D.6
11.某市出租车起步价所包含的路程为,超过的部分按每千米另收费.明明乘坐这种出租车走了,付了16元;盼盼乘坐这种出租车走了,付了28元.设这种出租车的起步价为元,超过后每千米收费元,则下列方程正确的是( )
A. B.
C. D.
12.“方程”二字最早见于我国《九章算术》这部经典著作中,该书的第八章名为“方程”如:从左到右列出的算筹数分别表示方程中未知数x,y的系数与相应的常数项,即可表示方程,则表示的方程是( )
A. B. C. D.
二、填空题
13.如图宽为的长方形图案是用8块相同的小长方形地砖拼成的,则每块小长方形地砖的长是
14.某车间有90名工人,每人每天平均能生产螺栓15个或螺帽24个,要使一个螺栓配套两个螺帽,应该如何分配工人才能便生产的螺栓和螺帽刚好配套?若设生产螺栓人,生产螺帽人,则列方程组得 .
15.甲、乙两种商品原来的单价之和为元,因市场变化,甲商品降价,乙商品提价,调价后两种商品的单价的和为元,甲、乙两种商品原来的单价相差 元.
16.《九章算术》中记载:“今有共买羊,人出五,不足四十五;人出七,不足三.问人数、羊价各几何?”其大意是:今有人合伙买羊,若每人出五钱,还差45钱;若每人出七钱,还差3钱.问合伙人数是多少?此问题中合伙人数为 .
17.我国古代数学名著《九章算术》中记载:今有甲乙两人持钱不知其数,甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?意思是现有甲乙两人,都不知道有多少钱,若乙把他一半的钱给甲,则甲有钱;而甲把他的钱给乙,则乙有50钱,问甲、乙各有多少钱?如果设甲原来有x钱,乙原来有y钱,则可列方程组为 .
三、解答题
18.某中学组织学生春游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满,已知45座客车每日每辆租金为220元,60座客车每日每辆租金为300元.试问:
(1)春游学生共多少人?原计划45座客车多少辆?
(2)若租用同一种车,要使每位同学都有座位,应该怎样租用才合算?
19.工作人员从仓库领取如图1中的长方形和正方形纸板作侧面和底面,做成如图2的竖式和横式的两种无盖纸盒若干个,恰好使领取的纸板用完.
(1)下表是工作人员两次领取纸板数的记录:
次数 正方形纸板(张) 长方形纸板(张)
第一次 560 940
第二次 420 1002
①仓库管理员在核查时,发现一次记录有误,请判断第几次的记录有误,并说明理由;
②记录正确的那一次,利用领取的纸板做了竖式和横式纸盒各多少个?
(2)若工作人员某次领取的正方形纸板数与长方形纸板数之比为1:3,请你求出利用这些纸板做出的竖式纸盒与横式纸盒个数的比值;
(3)拓展延伸:现在仓库里有张正方形纸板和张长方形纸板,如果做两种纸盒若干个,恰好使库存的纸板用完,则的值可能是( )
A.2013 B.2014 C.2015 D.2016
20.娄底市出租车收费规定:起步价所包含的路程为0~1.5千米,超过1.5千米的部分按每千米另收费.
刘同学说:“我乘出租车从市政府到娄底汽车站走了4.5千米,付车费11元.”
李同学说:“我乘出租车从市政府到娄底火车站走了6.5千米,付车费15元.”
问:
(1)出租车的起步价是多少元?超过1.5千米后每千米收费多少元?
(2)小张乘出租车从家里到娄底南站(高铁站)走了9.5千米,应付车费多少元?
21.某班决定购买两种绿植,已知购买A种绿植3盆和B种绿植4盆共需52元,购买A种绿植6盆和B种绿植5盆共需83元,问A种绿植和B种绿植每盆各多少元?
22.为迎接中考,很多同学购买了铅笔和涂卡尺.根据图中信息,求每支铅笔和每个涂卡尺的价格.
23.学校组织学生乘汽车去自然保护区野营,前路段为平路,其余路段为坡路.已知汽车在平路上行驶的速度为,在坡路上行驶的速度为.汽车从学校到自然保护区一共行驶了,求汽车在平路和坡路上各行驶了多长时间.
24.《张丘建算经》由北魏数学家张丘建所著,其中有这样一个问题:“今有客不知其数.两人共盘,少两盘;三人共盘,长三盘.问客及盘各几何?”意思为:“现有若干名客人.若2个人共用1个盘子,则少2个盘子;若3个人共用1个盘子,则多出来3个盘子.问客人和盘子各有多少?”请你解答这个问题.
《9.3二元一次方程组与实际问题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B A B B C A B B B
题号 11 12
答案 D A
1.D
【分析】本题是一道有关探究规律的题目,侧重考查知识点的应用能力,依题意,得,再解二元一次方程组即可.
【详解】解:依题意,得,
解得:,
故选:D.
2.B
【分析】根据鸡有两条腿,兔子有四条腿,共有20个头,60条腿,列出二元一次方程组即可.
【详解】解:由题意得:,
故选:B
【点睛】本题考查由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
3.A
【分析】本题二元一次方程组的应用,解题的关键是能够根据题意找到两个等量关系,这是列方程的依据.
找到两个等量关系列出方程组即可.
【详解】解:设一个生手工每天能制作x个零件,一个熟手工每天能制造y个零件,
根据题意得:,
故选A.
4.B
【分析】根据题意列出方程求出,的值,代入代数式求值即可.
【详解】解:根据题意得:,
解得:,,
.
故选:B.
【点睛】本题考查了有理数的加法,体现了方程思想,根据题意列出方程是解题的关键.
5.B
【解析】略
6.C
【分析】根据两台印刷机完成该任务共需和资料计划印制10000份,即可列出二元一次方程组.
【详解】解:∵两台印刷机完成该任务共需,
∴可列方程;
∵资料计划印制10000份,
∴可列方程,
∴甲和乙列的方程组都正确,
故选:C.
【点睛】本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
7.A
【分析】此题考查了二元一次方程组的实际应用,长方形的性质,根据长方形的两组对边分别相等列出方程组是解题的关键.
设一块长方形墙砖的长为,宽为,然后用的代数式分别表示出长方形的长为,两条宽分别为,,进而根据长方形的性质列出方程组,解方程组得到的值,再根据长方形面积计算公式即可求出面积,
【详解】解:设一块长方形墙砖的长为,宽为,依题意得,
,
解得,
∴每一块长方形墙砖的面积为:
答:每一块长方形墙砖的面积为.
故选:A.
8.B
【分析】本题考查的是二元一次方程组的应用,设雀每只两,燕每只两,根据“五只雀、六只燕,共重两,雀重燕轻.互换其中一只,恰好一样重”可列出方程组,从而可得答案.
【详解】解:设雀每只两,燕每只两,则可列出方程组为:
.
故选:B.
9.B
【分析】设个位数字为,十位数字为,根据“一个两位数的十位数字与个位数字的和是8”和“把这个两位数加上18,结果恰好成为数字对调后组成的两位数”列出方程组即可.
【详解】解:设个位数字为,十位数字为,
由题意得,,
故选:B
【点睛】此题考查了二元一次方程组的应用,读懂题意,找到两个等量关系是解题的关键.
10.B
【分析】根据三阶幻方中的数字列方程求解即可.
【详解】解:由题意,可得,
解得,
∴.
故选:B.
【点睛】本题主要考查二元一次方程组的应用以及零指数幂,熟练根据三阶幻方列方程求解是解题的关键.
11.D
【分析】本题主要考查由实际问题抽象出二元一次方程组.设这种出租车的起步价为x元,超过后每千米收费y元,根据题意列出二元一次方程组,即可求解.
【详解】解:设这种出租车的起步价为x元,超过后每千米收费y元,根据题意得,
,
故选:D.
12.A
【分析】本题考查了列二元一次方程,理解题意是解题的关键.根据横着的算筹为10,竖放的算筹为1,结合未知数的系数与等式后面的数字,即可求解.
【详解】
解:表示的方程是:
故选:A.
13.
【分析】首先设每块长方形的长是,宽是,然后根据图示列出关于x和y的二元一次方程组,从而求出x和y的值.
【详解】解:设每块长方形的长是,宽是,根据题意可得:
解得:
所以,长是,宽是.
故为答案:.
【点睛】此题考查方程组的应用问题,解题的关键是弄清题意,看懂图示,找出合适的等量关系,列出方程组,并弄清小长方形的长与宽的关系.
14.
【分析】根据某车间有90名工人,一个螺栓配套两个螺帽,列二元一次方程组即可.
【详解】解:根据题意,得,
故答案为: .
【点睛】本题考查了由实际问题抽象出二元一次方程组,理解题意并根据题意建立等量关系是解题的关键.
15.
【分析】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解答本题的关键.
设甲商品原来的单价为元,乙商品原来的单价为元,根据“甲、乙两种商品原来的单价之和为元,调价后两种商品的单价的和为元”,即可得出关于、的二元一次方程组,解之即可得出、的值,再将其代入中即可求出结论.
【详解】解:设甲商品原来的单价为元,乙商品原来的单价为元,
根据题意得,
解得,
,
故答案为:.
16.21
【分析】本题主要考查了二元一次方程组的应用.设合伙人数是x人,羊价为y元,根据“若每人出五钱,还差45钱;若每人出七钱,还差3钱.”列出方程组,即可求解.
【详解】解:设合伙人数是x人,羊价为y元,根据题意得:
,
解得:,
答:合伙人数是21人.
故答案为:21.
17.
【分析】本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.根据“若乙把他一半的钱给甲,则甲有钱”,“甲把他的钱给乙,则乙有钱” 即得出关于的二元一次方程组,即可求解.
【详解】解:由乙把他一半的钱给甲,则甲有钱,得
,
由甲把他的钱给乙,则乙有钱,得
,
可列方程组为.
故答案为:.
18.(1)七年级共有240人,计划租45座客车5辆
(2)租4辆60座更合算
【分析】(1)设七年级人数是x人,原计划租45座客车y辆,根据租用45座客车若干辆,但有15人没有座位,用同样数量的60座客车,则多出一辆车列出方程组,解方程组即可;
(2)分别算出租用同一种车时,需要的费用,然后进行比较即可.
【详解】(1)解:设七年级人数是x人,原计划租45座客车y辆,
由题意得:,
解得:
所以七年级共有240人,计划租45座客车5辆;
(2)解:只租45座需:
(元),
只租60座需: (元),
,
∴租4辆60座更合算.
【点睛】本题主要考查了二元一次方程的应用,解题的关键是根据等量关系,列出方程.
19.(1)①第二次,见解析;②做成40个竖式纸盒,260个横式纸盒
(2)3
(3)C
【分析】本题考查了二元一次方程组的应用,理解题意,找到正确的数量关系是本题的关键.
(1)①设做成x个竖式纸盒,y个横式纸盒,由领取的正方形的纸板和长方形的纸板之和应该是5的倍数,可判断第二次记录错误;
②由第一次记录,列出方程组,可求解;
(2)由正方形纸板数与长方形纸板数之比为1:3,可得,可求解;
(3)设做竖式和横式的两种无盖纸盒分别为x个、y个,然后根据所需长方形纸板和正方形纸板的张数列出方程组,再根据x、y的系数表示出并判断为5的倍数,然后选择答案即可.
【详解】(1)解:①第二次记录错误,
理由如下:设做成x个竖式纸盒,y个横式纸盒,
则需要正方形纸板张,需要长方形的纸板张,
∴领取的正方形的纸板和长方形的纸板之和为,应该是5的倍数,
而,,1422不能被5整除,
∴第二次记录有误;
②由题意可得:,
解得:,
答:做成40个竖式纸盒,260个横式纸盒;
(2)解:由题意可得:,
解得:,
∴,
答:竖式纸盒与横式纸盒个数的比值为3.
(3)解:设做竖式和横式的两种无盖纸盒分别为x个、y个,
根据题意得:,
两式相加得,,
∵x、y都是正整数,
∴是5的倍数,
∵2013、2014、2015、2016四个数中只有2015是5的倍数,
∴的值可能是2015.
故选:C.
20.(1)出租车的起步价是5元,超过1.5千米后每千米收费2元
(2)21元
【分析】(1)先设未知数,设出租车的起步价是x元,超过1.5千米后每千米收费y元.根据他们的对话建立2个等量关系,因为4.5千米和6.5千米都分两段收费,一段是1.5千米部分,一段是多于1.5千米的部分,再根据两段的单价和两人的付车费列出二元一次方程组求解;
(2)千米分两段收费:即1.5千米(起步价)+千米×单价=付车费.把(1)中的单价代入进行计算即可;
【详解】(1)解:设出租车的起步价是元,超过1.5千米后每千米收费元,
根据题意可得:,
即:,
解这个方程组,得:,
答:出租车的起步价是5元,超过1.5千米后每千米收费2元;
(2)小张应付的车费:(元),
答:小张应付的车费为21元.
【点睛】本题考查用二元一次方程组解决实际问题,解题关键弄清题中的等量关系.
21.A种绿植每盆8元,B种绿植每盆7元.
【分析】设A种绿植和B种绿植每盆x元和y元,根据“购买A种绿植3盆和B种绿植4盆共需52元,购买A种绿植6盆和B种绿植5盆共需83元”列方程组求解即可
【详解】解:设A种绿植和B种绿植每盆x元和y元,依题意,得
,
解方程得:
,
答:A种绿植每盆8元,B种绿植每盆7元.
【点睛】本题考查了二元一次方程组的应用,解题的关键是找准等量关系,正确的列出二元一次方程组.
22.每支2B铅笔和每个涂卡尺的价格分别为0.8元和1.5元
【分析】本题主要考查二元一次方程组的应用;设每支2B铅笔和每个涂卡尺的价格分别为元,元,根据题意,列出二元一次方程组,计算求解即可.
【详解】解:设每支2B铅笔和每个涂卡尺的价格分别为元,元,根据题意,
得
解得
答:每支2B铅笔和每个涂卡尺的价格分别为0.8元和1.5元.
23.汽车在平路上行驶了,在坡路上行驶了
【分析】本题考查的是二元一次方程组的应用,设汽车在平路上行驶了,在坡路上行驶了,再利用汽车从学校到自然保护区一共行驶了,前路段为平路,建立方程组求解即可.
【详解】解:设汽车在平路上行驶了,在坡路上行驶了,
由题意,得,
解得
答:汽车在平路上行驶了,在坡路上行驶了.
24.个客人,个盘子
【分析】本题考查二元一次方程,设有个客人,个盘子,根据题意列二元一次方程组并求解,找到正确的等量关系是解题的关键.
【详解】解:设有个客人,个盘子.
根据题意,得 ,
解得 ,
答∶有个客人,个盘子.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
