二次函数实践与探索
图片预览



文档简介
课件16张PPT。
§27.3二次函数的实践与探索
栾川县狮子庙初级中学:孟建会待定系数法求二次函数关系式几种方法
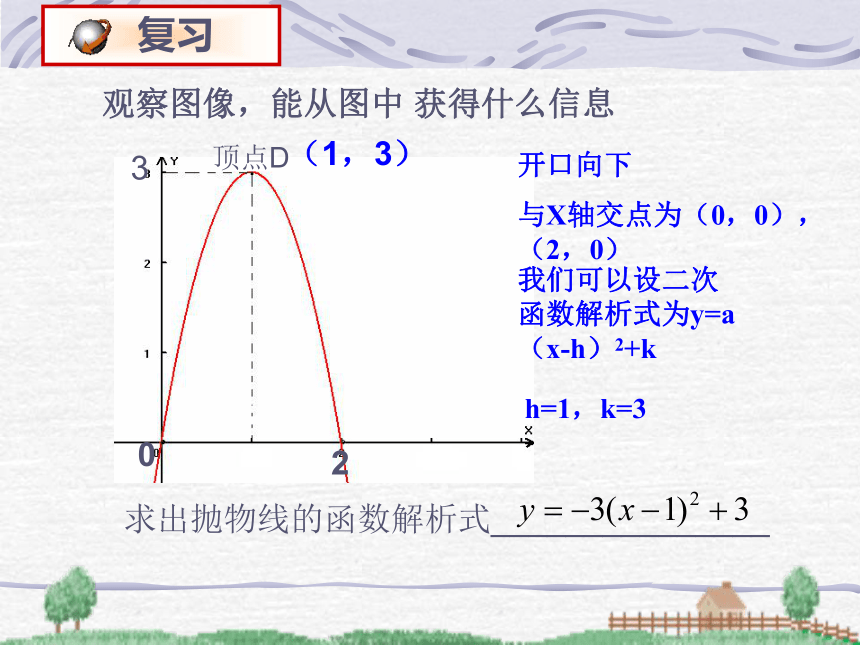
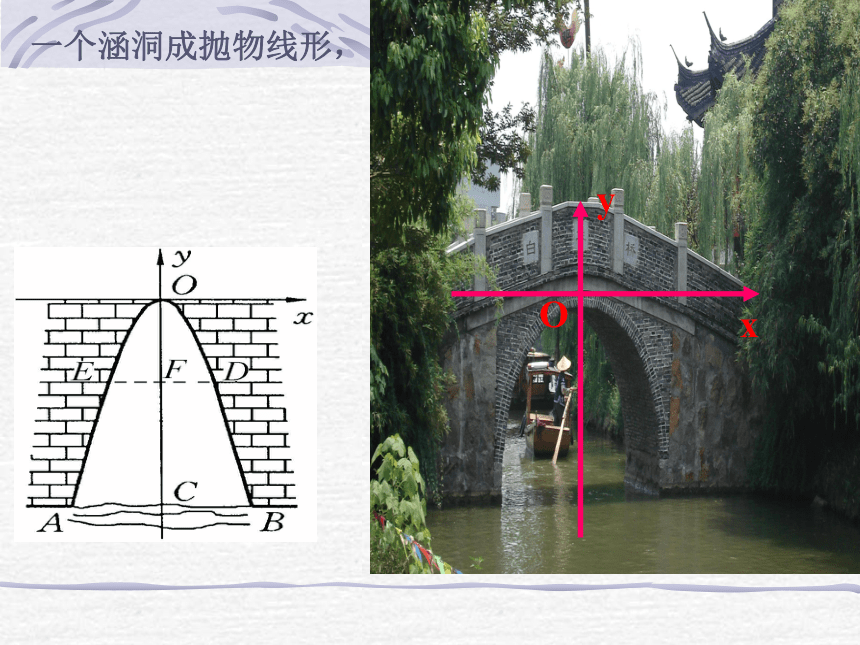
设一般式:设顶点式:设交点式:y=a(x-x1)(x-x2)(a≠0)x1,x2为函数图像与x轴交点的横坐标观察图像,能从图中 获得什么信息230求出抛物线的函数解析式_______________ (1,3)顶点D开口向下与X轴交点为(0,0),(2,0)我们可以设二次函数解析式为y=a(x-h)2+kh=1,k=3一个涵洞成抛物线形,xyO 一个涵洞成抛物线形,它的截面如图所示,现测得,
当水面宽AB=2米,涵洞顶点O与水面的距离为3米,
以O为原点,AB的中垂线为y轴,建立直角坐标系,1.直接写出A,B,O的坐标
2.求出抛物线的函数解析式3A(-1,-3) B(1,-3) O(0,0)探索一y=-3x2 一个涵洞成抛物线形,它的截面如图所示,现测得,
当水面宽AB=2米,涵洞顶点与水面的距离为3米,
以O为原点,AB的中垂线为y轴,建立直角坐标系,1.直接写出A,B,O的坐标
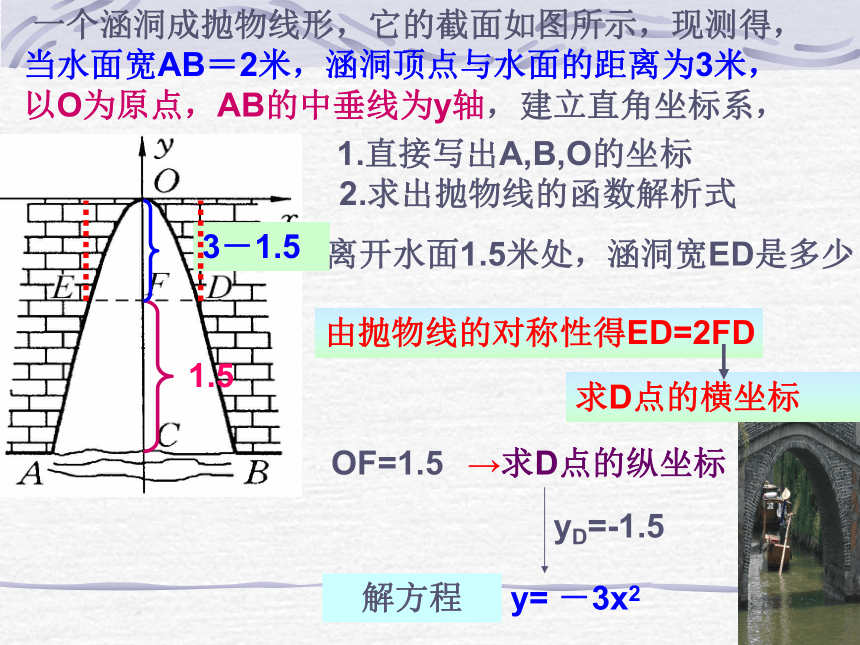
2.求出抛物线的函数解析式3.离开水面1.5米处,涵洞宽ED是多少
1.53-1.5OF=1.5→求D点的纵坐标由抛物线的对称性得ED=2FD求D点的横坐标yD=-1.5y= -3x2解方程一个涵洞成抛物线形,它的截面如图所示,现测得,
当水面宽AB=2米,涵洞顶点D与水面的距离为3米,(1)建立适当的直角坐标系(几种建法)
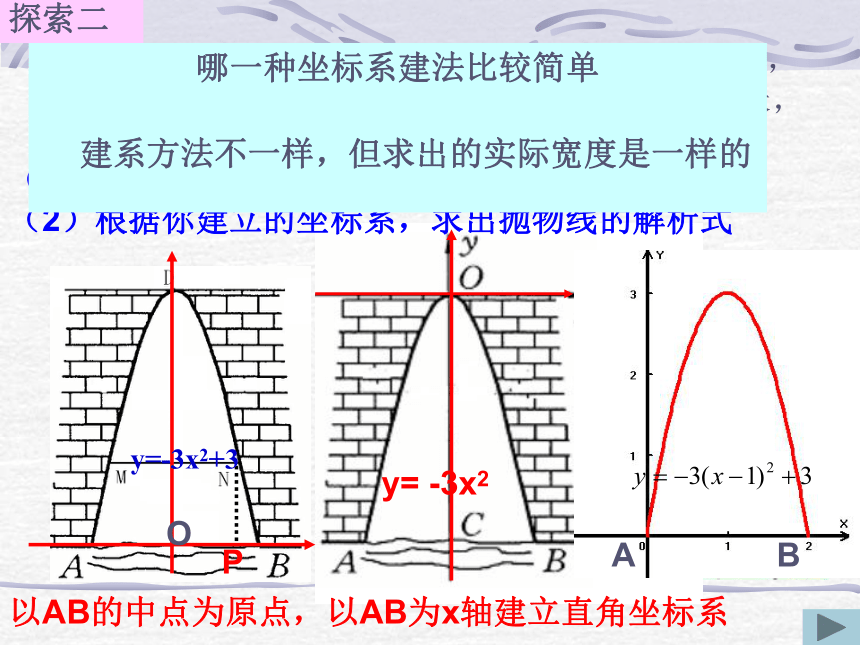
(2)根据你建立的坐标系,求出抛物线的解析式y= -3x2探索二若水面上涨1米,则此时的水面宽MN为多少 以AB的中点为原点,以AB为x轴建立直角坐标系O哪一种坐标系建法比较简单
建系方法不一样,但求出的实际宽度是一样的PABy=-3x2+3图像可通过平移而得到(4)又一个边长为1.6米的正方体木箱,能否通过此
涵洞,说明理由(木箱底面与水面同一平面)FEFNc1.6当通过的底为1.6时,能通过的最大高度为NF,比较NF与正方体的高(4)又一个边长为1.6米的正方体木箱,能否通过此
涵洞,说明理由(木箱底面与水面同一平面)FNc1.6当通过的底为1.6时,能通过的最大高度为NF,比较NF与正方体的高若箱子从涵洞正中通过,当通过的底为1.6时,能通过的最大高度为NF=1.5,小于正方体的高1.6,
所以不能通过
小结找点坐标建立变量与变量之间的函数关系式确定自变量的取值范围,保证自变量具有实际意义,解决问题把实际问题转化为点坐标他做的对吗?1.一个运动员推铅球,铅球在A点处出手,铅球的
飞行线路为抛物线铅球落地点为B,则这个运动员的成绩为__________米
2.
课后作业探索二O根据题目选择哪一种坐标系建法作业课本P27页第二题再见!
§27.3二次函数的实践与探索
栾川县狮子庙初级中学:孟建会待定系数法求二次函数关系式几种方法
设一般式:设顶点式:设交点式:y=a(x-x1)(x-x2)(a≠0)x1,x2为函数图像与x轴交点的横坐标观察图像,能从图中 获得什么信息230求出抛物线的函数解析式_______________ (1,3)顶点D开口向下与X轴交点为(0,0),(2,0)我们可以设二次函数解析式为y=a(x-h)2+kh=1,k=3一个涵洞成抛物线形,xyO 一个涵洞成抛物线形,它的截面如图所示,现测得,
当水面宽AB=2米,涵洞顶点O与水面的距离为3米,
以O为原点,AB的中垂线为y轴,建立直角坐标系,1.直接写出A,B,O的坐标
2.求出抛物线的函数解析式3A(-1,-3) B(1,-3) O(0,0)探索一y=-3x2 一个涵洞成抛物线形,它的截面如图所示,现测得,
当水面宽AB=2米,涵洞顶点与水面的距离为3米,
以O为原点,AB的中垂线为y轴,建立直角坐标系,1.直接写出A,B,O的坐标
2.求出抛物线的函数解析式3.离开水面1.5米处,涵洞宽ED是多少
1.53-1.5OF=1.5→求D点的纵坐标由抛物线的对称性得ED=2FD求D点的横坐标yD=-1.5y= -3x2解方程一个涵洞成抛物线形,它的截面如图所示,现测得,
当水面宽AB=2米,涵洞顶点D与水面的距离为3米,(1)建立适当的直角坐标系(几种建法)
(2)根据你建立的坐标系,求出抛物线的解析式y= -3x2探索二若水面上涨1米,则此时的水面宽MN为多少 以AB的中点为原点,以AB为x轴建立直角坐标系O哪一种坐标系建法比较简单
建系方法不一样,但求出的实际宽度是一样的PABy=-3x2+3图像可通过平移而得到(4)又一个边长为1.6米的正方体木箱,能否通过此
涵洞,说明理由(木箱底面与水面同一平面)FEFNc1.6当通过的底为1.6时,能通过的最大高度为NF,比较NF与正方体的高(4)又一个边长为1.6米的正方体木箱,能否通过此
涵洞,说明理由(木箱底面与水面同一平面)FNc1.6当通过的底为1.6时,能通过的最大高度为NF,比较NF与正方体的高若箱子从涵洞正中通过,当通过的底为1.6时,能通过的最大高度为NF=1.5,小于正方体的高1.6,
所以不能通过
小结找点坐标建立变量与变量之间的函数关系式确定自变量的取值范围,保证自变量具有实际意义,解决问题把实际问题转化为点坐标他做的对吗?1.一个运动员推铅球,铅球在A点处出手,铅球的
飞行线路为抛物线铅球落地点为B,则这个运动员的成绩为__________米
2.
课后作业探索二O根据题目选择哪一种坐标系建法作业课本P27页第二题再见!
