江西省南昌市2024-2025学年高三(下)4月月考(二模)数学试卷(含答案)
文档属性
| 名称 | 江西省南昌市2024-2025学年高三(下)4月月考(二模)数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 250.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 15:57:46 | ||
图片预览




文档简介
2024-2025学年江西省南昌市高三(下)4月月考
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.设,为两个不同的平面,则的一个充分条件是( )
A. 内有无数条直线与平行 B. ,平行于同一个平面
C. ,平行于同一条直线 D. ,垂直于同一个平面
2.已知复数满足,则( )
A. B. C. D.
3.已知集合,则( )
A. B. C. D.
4.在中,角,,的对边分别是,,,若,,则( )
A. B. C. D.
5.如图是江西省博物馆中典藏的元青白釉印花双凤纹碗,高,口径,若将该碗的内表面近似于一个球面的一部分,则这个球的半径近似于( )
A.
B.
C.
D.
6.已知、终边不重合,,则( )
A. B. C. D.
7.将双曲线绕其中心旋转一个合适的角度,可以得到一些熟悉的函数图象,比如反比例函数,“对勾”函数,“飘带”函数等等,它们的图象都能由某条双曲线绕原点旋转而得现将双曲线绕原点旋转一个合适的角度,得到“飘带”函数的图象,则双曲线的离心率为( )
A. B. C. D.
8.已知函数满足,且,则的最小值为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
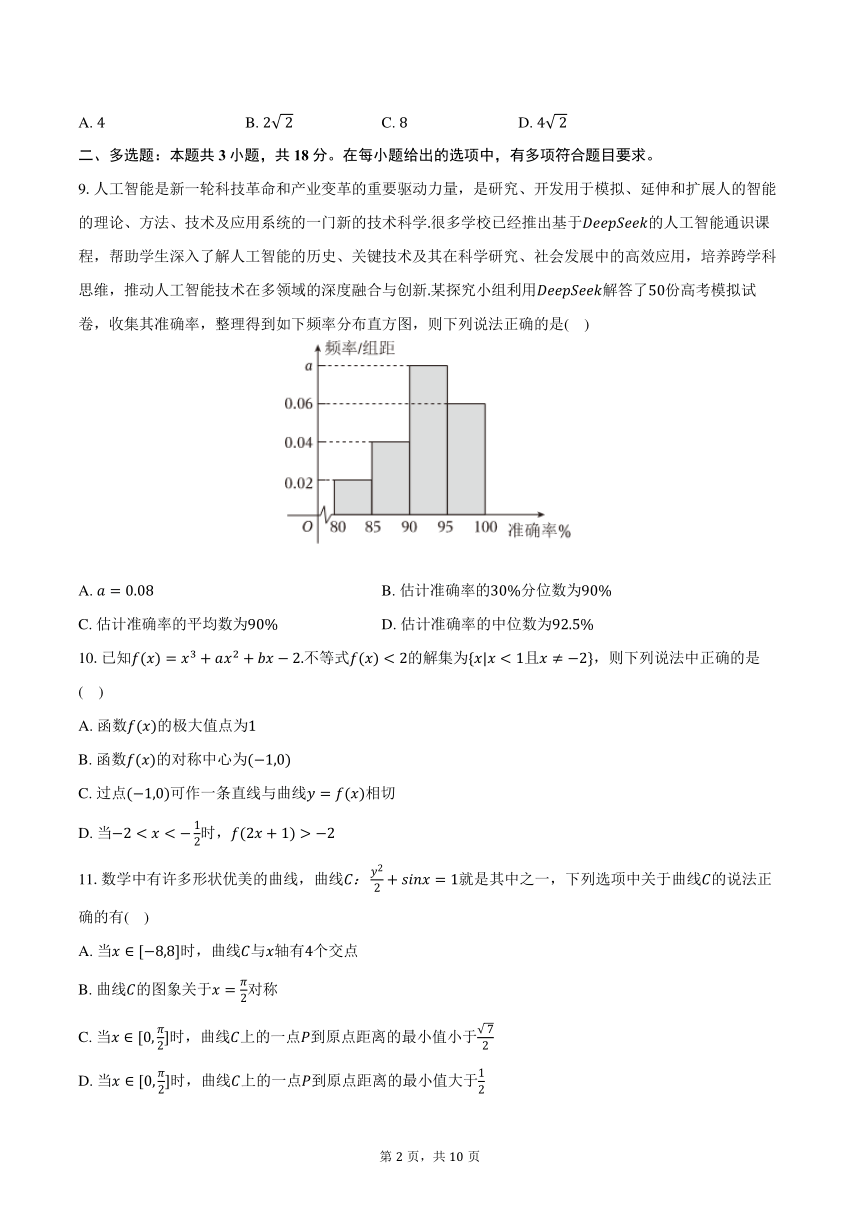
9.人工智能是新一轮科技革命和产业变革的重要驱动力量,是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学很多学校已经推出基于的人工智能通识课程,帮助学生深入了解人工智能的历史、关键技术及其在科学研究、社会发展中的高效应用,培养跨学科思维,推动人工智能技术在多领域的深度融合与创新某探究小组利用解答了份高考模拟试卷,收集其准确率,整理得到如下频率分布直方图,则下列说法正确的是( )
A. B. 估计准确率的分位数为
C. 估计准确率的平均数为 D. 估计准确率的中位数为
10.已知不等式的解集为且,则下列说法中正确的是( )
A. 函数的极大值点为
B. 函数的对称中心为
C. 过点可作一条直线与曲线相切
D. 当时,
11.数学中有许多形状优美的曲线,曲线就是其中之一,下列选项中关于曲线的说法正确的有( )
A. 当时,曲线与轴有个交点
B. 曲线的图象关于对称
C. 当时,曲线上的一点到原点距离的最小值小于
D. 当时,曲线上的一点到原点距离的最小值大于
三、填空题:本题共3小题,每小题5分,共15分。
12.已知函数,若,则 ______.
13.已知向量,,则的最小值是______.
14.某次庆典后,墙壁上的装饰品需要取下来,如图,由于材料特性,每次能取一个,且所取的装饰品只能有个或个相邻的装饰品,则不同的取法数有______种
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
在三棱柱中,侧面是边长为的正方形,,.
求证:平面平面;
求二面角的余弦值.
16.本小题分
已知抛物线:,过点作斜率大于直线与曲线交于、两点原点关于的对称点为记为点.
求证:;
当在抛物线上时,求的面积.
17.本小题分
为宣扬中国文化,某校组织古诗词知识比赛比赛分为两阶段,第一阶段为基础知识问答,每位选手都需要回答个问题,答对其中至少个问题,进入第二阶段,否则被淘汰;第二阶段分高分组、和低分组,第一阶段个问题都答对的选手进入高分组,共回答个问题,每答对一个得分,答错不得分;第一阶段答对个问题的选手进入低分组,共回答个问题,每答对一个得分,答错不得分第一阶段,每个问题选手甲答对的概率都是;第二阶段,若选手甲进入高分组,每个问题答对的概率都是,若选手甲进入低分组,每个问题答对的概率都是.
求选手甲第一阶段不被淘汰的概率;
求选手甲在该次比赛得分数为分的概率;
已知该次比赛选手甲进入了高分组,记选手甲在该次比赛中得分数为,求随机变量的分布列和期望值.
18.本小题分
已知.
当时,求函数的单调区间;
当时,求证:;
当,试讨论函数的零点个数.
19.本小题分
对于共项的等差数列公差不为各项重新排列得到新数列,若中的任意两项的等差中项都不在这两项所在位置之间,则称数列是等差数列的“无均数列”.
若,写出等差数列公差不为的个不同的“无均数列”;
若,写出等差数列公差不为的一个“无均数列”;
若,判断等差数列公差不为的“无均数列”是否存在,并证明你的结论.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:证明:因为侧面是边长为的正方形,
所以,,
因为,,
则,因为,
所以,即,
因为,、平面,
所以平面,又平面,
所以平面平面;
以直线,为,轴建立如图所示的空间直角坐标系,
因为,所以,
所以,
则,
设平面的法向量为,
则,由,可得,
令,则,
平面的法向量为,
所以,
又二面角为锐角,所以其余弦值为.
16.解:证明:设直线的方程为,、,
联立,消去并整理得,
此时,
由韦达定理得,,
所以,
则,
故;
因为原点关于的对称点为记为点,
此时,
解得,,
即,
因为点在抛物线上,
所以,
解得,
所以,,
则.
故.
17.解:选手甲第一阶段不被淘汰,即甲回答三个问题答对其中个或个,
其概率为:;
选手甲在该次比赛得分数为分有两种情况:进入高分组,答对个问题;进入低分组,答对个问题,
故概率为:;
由题意可知,的所有可能取值有,,,,,
则,,,
所以分布列为:
所以.
18.解:根据题目已知:
当时,,,
当时,,则在为增函数;
当时,,则在为减函数;
所以当时,函数的减区间为,增区间内为.
证明:因为,当时,,所以,
当时,,所以,所以,
设,由可知,所以不等式成立.
解法一:,
设,此时,
则,
因为,所以,
则在为减函数,,
当时,,结合在为减函数,
当时,,在为增函数;
当时,,在为减函数;
所以,所以,即在上为减函数,
又因为,所以只有一个零点;
当时,,
所以存在,使得,
当时,,所以在上增函数;
当时,,所以在上减函数.
因为,则,当,,
使得,
所以时,,即,即在为减函数;
当时,,即,即在为增函数;
当时,,即,即在为减函数;
当,,又因为,所以.
所以使得,
在为减函数,所以,所以存在两个零点.
综上所述:当时,函数有个零点;当函数有个零点.
19.解:根据题目定义:对于共项的等差数列公差不为各项重新排列得到新数列,
若中的任意两项的等差中项都不在这两项所在位置之间,则称数列是等差数列的“无均数列”.
当时,存在以下“无均数列”:
,,,;,,,;,,,;,,,;,,,;,,,;,,,;,,,;,,,;,,,,
总共种写出其中的个即可.
当时,存在“无均数列”:,,,,,,,.
证明:存在,
先证明对时,存在,
当时,由知存在“无均数列”,
假设时,存在“无均数列”,
则时,数列分成组,两组分别有次项,
且从这两组中各任取一项,得到的两项的等差中项不是的项,由假设,
数列存在“无均数列”,设为,
数列存在“无均数列”,设为,
构造数列:,
观察,每组之间的任意两个数的平均数均不在两数位置之间,故只需要考虑每组内部重新排成“无均数列”,
因此数列:,中任意两项的等差中项均不在这两项中间,
即时,数列存在“无均数列”,
由可知,时,都存在“无均数列”,
所以令,即时,存在“无均数列”,
接下来我们只需要将,,,项去掉,
便可得到时,等差数列存在“无均数列”.
同样注意到此时每一组是一共项的等差数列,
令,故由第二问知道,
此时只需要把其分为组,,,这样排列就能构成“无均”数列,
因此反复执行上述操作能把项的等差数列重新排列成一个“无均”数列,
所以当时也能重新排列成一个“无均”数列.
第1页,共1页
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.设,为两个不同的平面,则的一个充分条件是( )
A. 内有无数条直线与平行 B. ,平行于同一个平面
C. ,平行于同一条直线 D. ,垂直于同一个平面
2.已知复数满足,则( )
A. B. C. D.
3.已知集合,则( )
A. B. C. D.
4.在中,角,,的对边分别是,,,若,,则( )
A. B. C. D.
5.如图是江西省博物馆中典藏的元青白釉印花双凤纹碗,高,口径,若将该碗的内表面近似于一个球面的一部分,则这个球的半径近似于( )
A.
B.
C.
D.
6.已知、终边不重合,,则( )
A. B. C. D.
7.将双曲线绕其中心旋转一个合适的角度,可以得到一些熟悉的函数图象,比如反比例函数,“对勾”函数,“飘带”函数等等,它们的图象都能由某条双曲线绕原点旋转而得现将双曲线绕原点旋转一个合适的角度,得到“飘带”函数的图象,则双曲线的离心率为( )
A. B. C. D.
8.已知函数满足,且,则的最小值为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.人工智能是新一轮科技革命和产业变革的重要驱动力量,是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学很多学校已经推出基于的人工智能通识课程,帮助学生深入了解人工智能的历史、关键技术及其在科学研究、社会发展中的高效应用,培养跨学科思维,推动人工智能技术在多领域的深度融合与创新某探究小组利用解答了份高考模拟试卷,收集其准确率,整理得到如下频率分布直方图,则下列说法正确的是( )
A. B. 估计准确率的分位数为
C. 估计准确率的平均数为 D. 估计准确率的中位数为
10.已知不等式的解集为且,则下列说法中正确的是( )
A. 函数的极大值点为
B. 函数的对称中心为
C. 过点可作一条直线与曲线相切
D. 当时,
11.数学中有许多形状优美的曲线,曲线就是其中之一,下列选项中关于曲线的说法正确的有( )
A. 当时,曲线与轴有个交点
B. 曲线的图象关于对称
C. 当时,曲线上的一点到原点距离的最小值小于
D. 当时,曲线上的一点到原点距离的最小值大于
三、填空题:本题共3小题,每小题5分,共15分。
12.已知函数,若,则 ______.
13.已知向量,,则的最小值是______.
14.某次庆典后,墙壁上的装饰品需要取下来,如图,由于材料特性,每次能取一个,且所取的装饰品只能有个或个相邻的装饰品,则不同的取法数有______种
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
在三棱柱中,侧面是边长为的正方形,,.
求证:平面平面;
求二面角的余弦值.
16.本小题分
已知抛物线:,过点作斜率大于直线与曲线交于、两点原点关于的对称点为记为点.
求证:;
当在抛物线上时,求的面积.
17.本小题分
为宣扬中国文化,某校组织古诗词知识比赛比赛分为两阶段,第一阶段为基础知识问答,每位选手都需要回答个问题,答对其中至少个问题,进入第二阶段,否则被淘汰;第二阶段分高分组、和低分组,第一阶段个问题都答对的选手进入高分组,共回答个问题,每答对一个得分,答错不得分;第一阶段答对个问题的选手进入低分组,共回答个问题,每答对一个得分,答错不得分第一阶段,每个问题选手甲答对的概率都是;第二阶段,若选手甲进入高分组,每个问题答对的概率都是,若选手甲进入低分组,每个问题答对的概率都是.
求选手甲第一阶段不被淘汰的概率;
求选手甲在该次比赛得分数为分的概率;
已知该次比赛选手甲进入了高分组,记选手甲在该次比赛中得分数为,求随机变量的分布列和期望值.
18.本小题分
已知.
当时,求函数的单调区间;
当时,求证:;
当,试讨论函数的零点个数.
19.本小题分
对于共项的等差数列公差不为各项重新排列得到新数列,若中的任意两项的等差中项都不在这两项所在位置之间,则称数列是等差数列的“无均数列”.
若,写出等差数列公差不为的个不同的“无均数列”;
若,写出等差数列公差不为的一个“无均数列”;
若,判断等差数列公差不为的“无均数列”是否存在,并证明你的结论.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:证明:因为侧面是边长为的正方形,
所以,,
因为,,
则,因为,
所以,即,
因为,、平面,
所以平面,又平面,
所以平面平面;
以直线,为,轴建立如图所示的空间直角坐标系,
因为,所以,
所以,
则,
设平面的法向量为,
则,由,可得,
令,则,
平面的法向量为,
所以,
又二面角为锐角,所以其余弦值为.
16.解:证明:设直线的方程为,、,
联立,消去并整理得,
此时,
由韦达定理得,,
所以,
则,
故;
因为原点关于的对称点为记为点,
此时,
解得,,
即,
因为点在抛物线上,
所以,
解得,
所以,,
则.
故.
17.解:选手甲第一阶段不被淘汰,即甲回答三个问题答对其中个或个,
其概率为:;
选手甲在该次比赛得分数为分有两种情况:进入高分组,答对个问题;进入低分组,答对个问题,
故概率为:;
由题意可知,的所有可能取值有,,,,,
则,,,
所以分布列为:
所以.
18.解:根据题目已知:
当时,,,
当时,,则在为增函数;
当时,,则在为减函数;
所以当时,函数的减区间为,增区间内为.
证明:因为,当时,,所以,
当时,,所以,所以,
设,由可知,所以不等式成立.
解法一:,
设,此时,
则,
因为,所以,
则在为减函数,,
当时,,结合在为减函数,
当时,,在为增函数;
当时,,在为减函数;
所以,所以,即在上为减函数,
又因为,所以只有一个零点;
当时,,
所以存在,使得,
当时,,所以在上增函数;
当时,,所以在上减函数.
因为,则,当,,
使得,
所以时,,即,即在为减函数;
当时,,即,即在为增函数;
当时,,即,即在为减函数;
当,,又因为,所以.
所以使得,
在为减函数,所以,所以存在两个零点.
综上所述:当时,函数有个零点;当函数有个零点.
19.解:根据题目定义:对于共项的等差数列公差不为各项重新排列得到新数列,
若中的任意两项的等差中项都不在这两项所在位置之间,则称数列是等差数列的“无均数列”.
当时,存在以下“无均数列”:
,,,;,,,;,,,;,,,;,,,;,,,;,,,;,,,;,,,;,,,,
总共种写出其中的个即可.
当时,存在“无均数列”:,,,,,,,.
证明:存在,
先证明对时,存在,
当时,由知存在“无均数列”,
假设时,存在“无均数列”,
则时,数列分成组,两组分别有次项,
且从这两组中各任取一项,得到的两项的等差中项不是的项,由假设,
数列存在“无均数列”,设为,
数列存在“无均数列”,设为,
构造数列:,
观察,每组之间的任意两个数的平均数均不在两数位置之间,故只需要考虑每组内部重新排成“无均数列”,
因此数列:,中任意两项的等差中项均不在这两项中间,
即时,数列存在“无均数列”,
由可知,时,都存在“无均数列”,
所以令,即时,存在“无均数列”,
接下来我们只需要将,,,项去掉,
便可得到时,等差数列存在“无均数列”.
同样注意到此时每一组是一共项的等差数列,
令,故由第二问知道,
此时只需要把其分为组,,,这样排列就能构成“无均”数列,
因此反复执行上述操作能把项的等差数列重新排列成一个“无均”数列,
所以当时也能重新排列成一个“无均”数列.
第1页,共1页
同课章节目录
