第七章 万有引力与宇宙航(含解析)行单元检测高中物理人教版(2019)必修 第二册
文档属性
| 名称 | 第七章 万有引力与宇宙航(含解析)行单元检测高中物理人教版(2019)必修 第二册 |  | |
| 格式 | docx | ||
| 文件大小 | 614.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-04-21 16:00:34 | ||
图片预览




文档简介
第七章万有引力与宇宙航行
一、单选题
1.与地球公转轨道“外切”的小行星甲和“内切”的小行星乙的公转轨道如图所示,假设这些小行星与地球的公转轨道都在同一平面内,已知地球的公转半径为,公转周期为,小行星甲的远日点到太阳的距离为,小行星乙的近日点到太阳的距离为,引力常量为,下列说法正确的是( )
A. 小行星甲与太阳的连线和小行星乙与太阳的连线在相同时间内扫过的面积相等
B. 小行星乙在远日点的加速度大小等于地球公转的加速度大小
C. 小行星甲的公转周期为
D. 太阳的密度为
2.北京时间年月日时分,搭载神舟十八号载人飞船的长征二号遥十八运载火箭在酒泉卫星发射中心成功发射,日清晨神十八乘组抵达中国空间站。航天员叶光富、李聪、李广苏进入核心舱开展相关工作。已知核心舱的运行轨道距地面高度约为,地球的半径为,地球表面的重力加速度为,引力常量为,忽略地球自转的影响,下列说法正确的是( )
A. 地球的质量可表示为
B. 地球的平均密度可表示为
C. 核心舱的运行速度大小介于和之间
D. 核心舱的运行速度大小为
3.星球上的物体脱离星球引力所需要的最小发射速度称为第二宇宙速度,星球的第二宇宙速度与第一宇宙速度的关系是。已知某星球的半径为,它表面的重力加速度为地球表面重加速度的,不计其他星球的影响,则该星球的第二宇宙速度为( )
A. B. C. D.
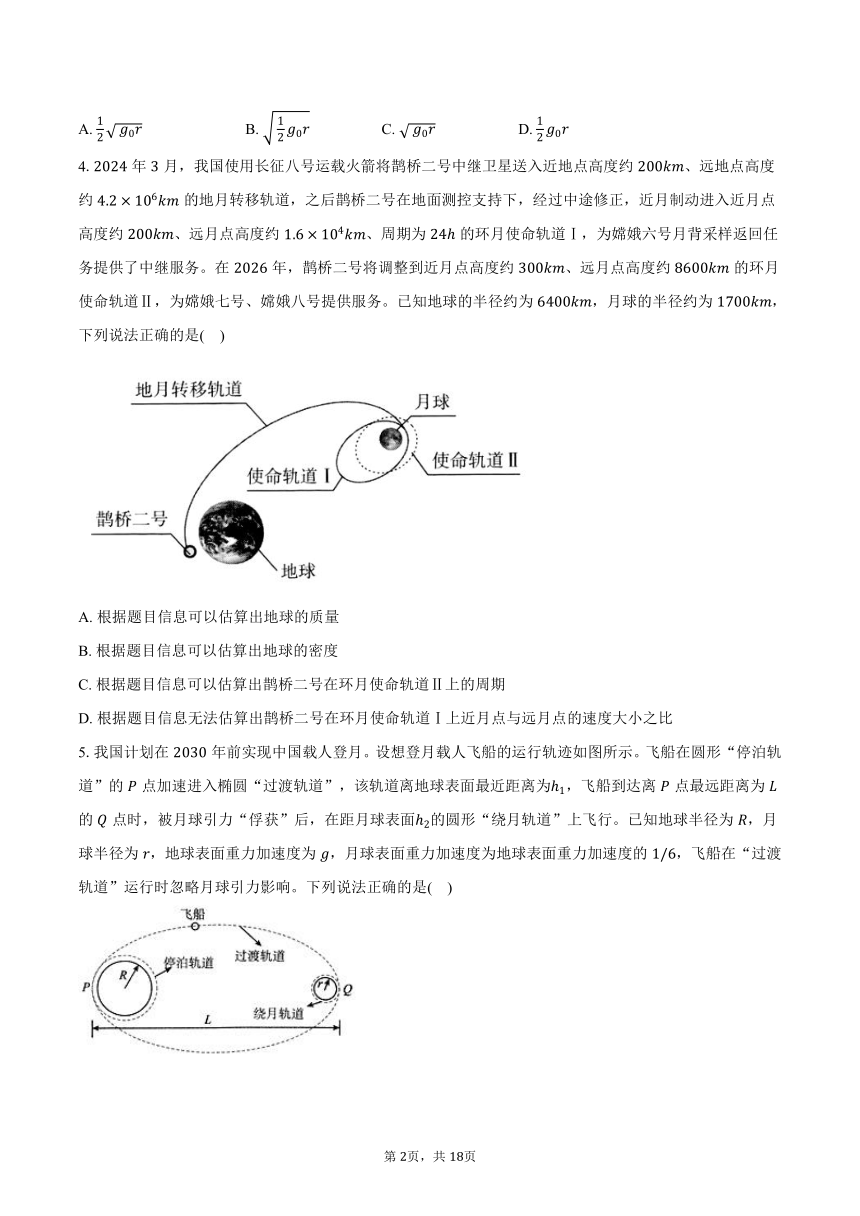
4.年月,我国使用长征八号运载火箭将鹊桥二号中继卫星送入近地点高度约、远地点高度约的地月转移轨道,之后鹊桥二号在地面测控支持下,经过中途修正,近月制动进入近月点高度约、远月点高度约、周期为的环月使命轨道Ⅰ,为嫦娥六号月背采样返回任务提供了中继服务。在年,鹊桥二号将调整到近月点高度约、远月点高度约的环月使命轨道Ⅱ,为嫦娥七号、嫦娥八号提供服务。已知地球的半径约为,月球的半径约为,下列说法正确的是( )
A. 根据题目信息可以估算出地球的质量
B. 根据题目信息可以估算出地球的密度
C. 根据题目信息可以估算出鹊桥二号在环月使命轨道Ⅱ上的周期
D. 根据题目信息无法估算出鹊桥二号在环月使命轨道Ⅰ上近月点与远月点的速度大小之比
5.我国计划在年前实现中国载人登月。设想登月载人飞船的运行轨迹如图所示。飞船在圆形“停泊轨道”的点加速进入椭圆“过渡轨道”,该轨道离地球表面最近距离为,飞船到达离点最远距离为的点时,被月球引力“俘获”后,在距月球表面的圆形“绕月轨道”上飞行。已知地球半径为,月球半径为,地球表面重力加速度为,月球表面重力加速度为地球表面重力加速度的,飞船在“过渡轨道”运行时忽略月球引力影响。下列说法正确的是( )
A. 飞船的发射速度必须大于
B. 飞船在“过渡轨道”上点加速度大于“停泊轨道”上点的加速度
C. 飞船在“过渡轨道”上的点运行速度为
D. 飞船从点运动到点的时间为
6.年月日时分,我国神舟十八号载人飞船采用自主快速交会对接模式,成功对接于中国空间站天和核心舱径向端口如图所示,随后名航天员从神舟十八号载人飞船进入中国空间站开展为期六个月的太空工作与生活,这次太空远航,航天员们携带了一个叫做“小受控型生态生命模块”的装置及相关物品进入太空,其中的主要水生生命体就是斑马鱼和金鱼藻,实现我国在外太空培养脊椎动物的首次突破。已知空间站绕地球运行的轨道半径为,地球半径为,地球表面的重力加速度为。则以下判断中正确的是( )
A. 空间站绕地球稳定飞行时,斑马鱼受到万有引力和浮力作用
B. 空间站绕地球飞行速度大于第一宇宙速度
C. 空间站运行的速度大小为
D. 质量为的金鱼藻在空间站所受万有引力的大小为
7.神舟十八号名航天员在轨驻留天,期间进行了次出舱活动,刷新了中国航天员单次出舱活动时间纪录。可近似认为天宫空间站在距离地面高度约为的圆轨道上做匀速圆周运动,地球半径为,不考虑地球自转,地表重力加速度取,出舱活动期间,航天员相对天宫空间站处于静止状态。下列说法正确的是
A. 出舱活动期间,航天员受到的合外力为
B. 空间站运行速度大小约为
C. 空间站运行的向心加速度大小约为
D. 返回舱与天宫空间站分离后,返回地球需要点火加速
8.如图所示,卫星没有发射,停放在地球的赤道上随地球自转;卫星发射成功,在地球赤道上空贴着地表做匀速圆周运动;两卫星的质量相等.认为重力近似等于万有引力.下列说法正确的是( )
A. 、做匀速圆周运动所需的向心力大小相等
B. 做匀速圆周运动的向心加速度等于重力加速度
C. 、做匀速圆周运动的线速度大小相等,都等于第一宇宙速度
D. 做匀速圆周运动的周期大于地球同步卫星的周期
9.我国科研人员利用“探测卫星”获取了某一未知星球的探测数据,如图所示,图线表示“探测卫星”绕该星球运动的关系图像,表示“探测卫星”绕地球运动的关系图像,其中是卫星绕中心天体运动的轨道半径,是对应的周期。“探测卫星”在该星球近表面和地球近表面运动时均满足,图中、、已知,则( )
A. 该星球和地球的质量之比为
B. 该星球和地球的第一宇宙速度之比为
C. 该星球和地球的密度之比为
D. 该星球和地球表面的重力加速度大小之比为
10.甲同学在北极以某一初速度竖直上抛一个小球,经过一段时间落回手中;乙同学在赤道以相同速度竖直上抛另一小球,经过另一段时间落回手中。已知甲、乙抛出小球对应的运动时间的比值为,不考虑空气阻力,则地球第一宇宙速度与地球同步卫星的线速度之比为( )
A. B. C. D.
11.我国成功将“高分十三号”卫星发射升空并顺利进入地球同步轨道。“高分十三号”卫星是一颗高轨光学遥感卫星,可为国民经济发展提供信息服务。研究表明,地球自转在逐渐变慢,亿年前地球自转的周期约为小时。假设这种趋势会持续下去,地球的其他条件都不变。则( )
A. 未来地球的第一宇宙速度小于
B. 未来赤道的重力加速度将逐渐变大
C. 未来极地的重力加速度将逐渐变小
D. 未来人类发射的地球同步卫星与“高分十三号”卫星相比轨道半径将变小
二、多选题
12.在地球表面,被轻质细线悬挂而处于静止状态的质量为的小球,所受地球的万有引力作用效果分解示意图如图所示,已知小球所处的纬度为,重力为,万有引力为,地球的半径为,自转周期为,下列说法正确的是( )
A. 细线的拉力与的合力提供了小球做圆周运动的向心力
B. 小球所需的向心力为
C. 地球赤道处的重力加速度为
D. 地球的第一宇宙速度为
13.土星是太阳系中的第二大行星,距离地球约亿千米如图所示为发射土星探测器的简易图,探测器经地土转移轨道后,经停泊轨道、,最后到达探测轨道已知土星的半径约为地球半径的倍,质量约为地球质量的倍,地球表面的重力加速度大小为,下列说法正确的是( )
A. 探测器的发射速度一定大于
B. 土星表面的重力加速度大小为
C. 探测器在轨道、、的运行周期关系为
D. 探测器在轨道经点的速度小于轨道经点的速度
14.如图所示,飞船在离地球表面高处的轨道上做周期为的匀速圆周运动,已知地球的半径,则:( )
A. 飞船在该轨道上运行的线速度大于第一宇宙速度
B. 飞船在该轨道上运行的线速度大小为
C. 飞船在该轨道上运行时的向心加速度大小为
D. 地球表面的重力加速度大小可表示为
15.如图所示,飞行器绕半径为的某行星做匀速圆周运动,星球相对飞行器的张角为,其环绕周期为,引力常量为,行星可视为质量均匀分布的球体,不考虑行星的自转,下列说法正确的是( )
A. 行量的质量为 B. 行星的平均密度为
C. 行星表面的重力加速度为 D. 行星的第一宇宙速度为
三、实验题
16.月地检验
检验目的:检验地球绕太阳运动、月球绕地球运动的力与地球对树上苹果的引力是否为_______________的力。
检验方法:
假设地球与月球间的作用力和太阳与行星间的作用力是同一种力,它们的表达式也应该满足。
根据牛顿第二定律,月球绕地球做圆周运动的向心加速度式中地是地球质量,是地球中心与月球中心的距离。
假设地球对苹果的吸引力也是同一种力,同理可知,苹果的自由落体加速度式中地是地球的质量,是地球中心与苹果间的距离。
,由于,所以。
验证:
苹果自由落体加速度苹
月球中心到地球中心的距离。
月球公转周期
则月___________保留两位有效数字____________数值比例。
结论:地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力遵从_________________的规律。
17.年月日下午,“天宫课堂”第二课在中国空间站开讲,王亚平做了太空抛物实验,奥运顶流“冰墩墩”在空间站上被航天员抛出后,并没有像在地面上那样做曲线运动,而是水平飞出去了。
请根据此实验回答以下问题:
关于冰墩墩被水平抛出后,做水平运动的原因,以下解释中正确的是_________;
A.冰墩墩在空间站内不受力的作用
B.冰墩墩水平方向不受外力作用
C.冰墩墩处于完全失重的状态
D.冰墩墩随空间站绕地球做匀速圆周运动,万有引力提供向心力
历史上,牛顿曾提出:若在地球表面的高山上来做平抛实验,把物体抛出,它将落向地面;如果将物体抛出的速度变大,它将会落向更远的地方。如果抛出的速度足够大,它有可能不落回地面,而是绕地球运转。已知地球半径为,小伟同学用如下方法推导这一速度:
其结果与正确值相差很远,这是由于他在近似处理中,错误的假设是_________;
A.卫星的轨道是圆的 卫星的轨道半径等于地球半径
C.卫星的周期等于地球自转的周期 卫星的向心力等于它在地球上受到的地球引力
已知地球表面重力加速度,请你利用已学习的物理知识求出正确的“足够大的速度”为_________。保留位有效数字
四、计算题
18.年月日,我国文昌卫星发射中心成功将中星卫星发射升空.若卫星在距地球表面某高度处绕地球做匀速圆周运动的周期为,已知地球表面的重力加速度为,地球可视为均匀球体,其半径为,引力常量为,忽略地球自转影响.求:
地球的质量;
卫星距地球表面的高度.
19.如图所示,假定地球为密度均匀分布的球体,忽略地球的自转,已知地球的半径为。理论和实验证明:质量均匀分布的球壳对壳内物体的万有引力为零。求:
地面上方高的山顶处和地面处重力加速度大小之比
地面下方深的矿井底处和地面处重力加速度大小之比
根据上述两问的结论,定性做出重力加速度随离地心的距离而变化的函数关系式上图中为地球半径,为地球表面处的重力加速度。
20.如图,已知地球半径为,地球表面的重力加速度为,不考虑地球自转的影响,飞船先在近地轨道Ⅲ上绕地球做圆周运动,到达轨道Ⅲ的点时点火变轨进入椭圆轨道Ⅱ,到达轨道Ⅱ的远地点时再次点火进入轨道Ⅰ绕地球做圆周运动,轨道Ⅰ的轨道半径为,求:
从地球发射飞船到轨道Ⅲ的最小速度
飞船在轨道Ⅰ上的运行速率
飞船在轨道Ⅱ从点到点的时间.
21.宇宙间存在一些离其他恒星较远的三星系统,其中一种三星系统如图所示。三颗质量均为的星体位于等边三角形的三个顶点,三角形边长为。忽略其他星体对它们的引力作用,三星在同一平面内绕三角形中心做匀速圆周运动,万有引力常量为,,
求每颗星的加速度大小;
每颗星做匀速圆周运动的周期;
若等边三角形的边长与每颗星的质量都变成两倍,则每颗星的线速度大小与之前线速度的比。
答案和解析
1.【答案】
【解析】A.根据开普勒第二定律可知,同一行星与太阳的连线在相同时间内扫过的面积相等,但小行星甲与小行星乙在不同轨道上,所以小行星甲与太阳的连线和小行星乙与太阳的连线在相同时间内扫过的面积不相等,故A错误;
B.根据牛顿第二定律可得
可得
由于小行星乙在远日点离太阳距离等于地球离太阳距离,则小行星乙在远日点的加速度大小等于地球公转的加速度大小,故B正确;
C.根据开普勒第三定律可得
解得小行星甲的公转周期为
故C错误;
D.设太阳质量为 ,太阳半径为 ,太阳的密度为 ,则有
地球绕太阳转动,由万有引力提供向心力可得
联立可得太阳的密度为
故D错误。
故选B。
2.【答案】
【解析】A.设地球的质量为,不考虑地球自转的影响,地面上质量为的物体所受的重力等于地球对物体的引力,即,解得:,故A错误;
B.地球的平均密度为,故B错误;
C.第一宇宙速度为最大的环绕速度,核心舱的运行速度小于第一字宙速度,即小于,故C错误;
D.核心舱所受万有引力提供向心力有:,结合,解得,故D正确。
3.【答案】
【解析】解:在星球表面,重力等于其表面卫星的环绕速度,根据牛顿第二定律,有:
解得:
根据题意,有:
故
故选:
4.【答案】
【解析】设鹊桥二号在地月转移轨道上的近地点的高度为,远地点的高度为,地球的直径为,鹊桥二号的运行周期为,根据开普勒第三定律可得
根据牛顿第二定律和万有引力定律
则
解得
由于引力常量与周期未知,故地球的质量和密度无法求得,故AB错误;
C.设环月使命轨道Ⅰ的近月点高度为,远月点高度为,环月使命轨道Ⅱ的近月点高度为,远月点高度为,月球的直径为,题目中已知鹊桥二号在环月使命轨道上的周期为,根据开普勒第三定律,可以求得鹊桥二号在环月使命轨道Ⅱ上的周期为,故C正确;
D.设鹊桥二号在环月使命轨道Ⅰ上近月点与远月点的速度大小分别为和,近月点到月心的距离,远月点到月心的距离,根据开普勒第二定律,解得,故D错误。
5.【答案】
【解析】A、飞船运动中未脱离地球引力的束缚,其发射速度大于第一宇宙速度而小于第二宇宙速度,地球的第二宇宙速度为,则飞船的发射速度一定小于,故A错误;
B、由知,飞船在“过渡轨道”上点加速度等于“停泊轨道”上点的加速度,故B错误;
C、由卫星变轨知,飞船在“过渡轨道”上的点运行速度大于其在停泊轨道上运动的速度,题设条件不足,无法计算出飞船在“过渡轨道”上的点运行速度,故C错误;
D、飞船在停泊轨道运动时,由牛顿第二定律:,在地球表面:,由开普勒第三定律:,联立知,飞船从点运动到点的时间为,故D正确。
6.【答案】
【解析】空间站绕地球稳定飞行时,万有引力提供向心力,处于完全失重状态,所以斑马鱼只受万有引力作用,不受浮力作用,A错误
地球第一宇宙速度是卫星绕地球做匀速圆周运动的最大线速度,可知空间站绕地飞行速度小于第一宇宙速度,B错误
根据万有引力与重力的关系有,根据万有引力提供向心力有,解得空间站的速度大小为,C错误
质量为的金鱼藻在空间站所受万有引力的大小为,根据万有引力与重力的关系得,解得,D正确。
7.【答案】
【解析】解析: 出舱活动期间,航天员做绕地球的匀速圆周运动,受到的合外力提供向心力,受到的合外力不为, 故A错误
地球对空间站的万有引力提供空间站做匀速圆周运动需要的向心力,可得: , 又因为在地球表面有: ,联立两式可得: ,第一宇宙速度 可知B错误 , ,故C正确
返回舱与天宫空间站分离后,返回地球时,根据变轨规律知,需要点火减速,故 D错误.
8.【答案】
【解析】A、两卫星的质量相等,到地心的距离相等,所以受到地球的万有引力相等.卫星在赤道上随地球自转而做圆周运动,万有引力的一部分提供自转的向心力,卫星在赤道上空贴着地表做匀速圆周运动,万有引力全部用来提供公转的向心力,因此、做匀速圆周运动所需的向心力大小不相等,项错误;
B、对卫星,重力近似等于万有引力,万有引力全部用来提供向心力,所以向心加速度等于重力加速度,项正确;
C、卫星在赤道上空贴着地表做匀速圆周运动,其速度就是最大的环绕速度,也是第一宇宙速度,卫星在赤道上随地球自转而做圆周运动,向心力小于卫星的向心力,根据牛顿第二定律,卫星的线速度小于的线速度,即的线速度小于第一宇宙速度,项错误;
D、在赤道上随地球自转而做圆周运动,自转周期等于地球的自转周期,同步卫星的周期也等于地球的自转周期,所以做匀速圆周运动的周期等于地球同步卫星的周期,项错误.
故选B。
9.【答案】
【解析】A.根据万有引力提供向心力有,解得,可知图像的斜率为,故该星球和地球的质量之比,故A错误;
B.“探测卫星”在该星球近表面和地球近表面运动时均满足,即,可得,根据万有引力提供向心力有,解得,故该星球和地球的第一宇宙速度之比,故B正确;
C.星球的体积为,密度为,故该星球和地球的密度之比为,故C错误;
D.在星球表面,万有引力与重力的关系有,解得,故该星球和地球表面的重力加速度大小之比为,故D错误。
10.【答案】
【解析】设小球的初速度为,在北极小球运动的时间为,重力加速度为在赤道小球运动的时间为,重力加速度为,由竖直上抛,可得,,则
设地球半径为,在北极,
在赤道,,为地球自转周期。
设地球第一宇宙速度大小为,同步卫星的线速度大小为,周期与地球自转周期相等也为,
由,
同步卫星,,
联立以上各式解得,A正确。
11.【答案】
【解析】A、地球半径为,质量为,根据可得,可见第一宇宙速度与地球自转周期无关,而且第一宇宙速度是,不是,故A错误;
、在赤道上有,在两极有,
地球自转在逐渐变慢,即自转周期变大,则未来赤道的重力加速度将逐渐变大,极地的重力加速度不变,故B正确,C错误;
D、根据,可得同步卫星轨道半径,变大,则轨道半径变大,故D错误。
故选B。
12.【答案】
【解析】A.细线的拉力 与的合力提供了小球做圆周运动的向心力,故A正确;
B.小球做圆周运动的半径为 ,所以小球所需的向心力为
故B错误;
C.小球所处的纬度重力为 大于赤道处的重力,所以地球赤道处的重力加速度小于 ,故C错误;
D.根据 可得地球的第一宇宙速度为
故D正确。
13.【答案】
【解析】探测器需要到达土星,因此最终会脱离地球的引力束缚,但还在太阳系中,故发射速度应大于,小于,A错误
由万有引力等于重力,有,解得,故土星表面的重力加速度大小,B正确
由开普勒第三定律,有,可知轨道的半长轴最大、轨道的轨道半径最小,所以探测器在轨道、、的运行周期关系为,C正确
探测器在轨道上经过点后做离心运动,有,探测器在轨道上经过点做匀速圆周运动,有,故,D错误.
14.【答案】
【解析】、研究飞船绕地球做匀速圆周运动,根据万有引力提供向心力,列出等式:
,其中为地球质量,为轨道半径,
飞船在离地球表面 高处的轨道上做周期为的匀速圆周运动,飞船的轨道半径,
第一宇宙速度是近地卫星的环绕速度,也是最大的圆周运动的环绕速度,所以飞船运行的线速度小于第一宇宙速度,故A错误.
B、根据圆周运动知识得:运行的线速度大小,故B正确.
C、根据圆周运动知识得:运行时的向心加速度大小,故C正确.
D、,得:
忽略地球自转的影响,在地球表面根据万有引力等于重力列出等式:
由得:地球表面的重力加速度大小故D错误。
15.【答案】
【解析】由题意可得,M=ρ 4/3 πr^3,故选:。
16.【答案】同一性质 相同
【解析】月地检验的目的就是检验地球绕太阳运动、月球绕地球运动的力与地球对树上苹果的引力是否是同一种性质的力。
已知,
已知,。
先计算的值:,。则保留两位有效数字。
已知,,
则。
通过月地检验,计算出的的值与理论推导相符,说明地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力遵从相同的规律。
17.【答案】;;
【解析】冰墩墩在空间站内受地球等的万有引力作用,故A错误;
冰墩墩随空间站绕地球做匀速圆周运动,万有引力提供向心力,处于完全失重状态,由于万有引力指向地心,则冰墩墩水平方向不受外力作用,故BCD正确;
故选:。
如果抛出的速度足够大,它有可能不落回地面,而是绕地球运转,由万有引力提供向心力,做匀速圆周运动,假设正确,不符合题意;
B.由于山的高度远小于地球的半径,则该卫星的轨道半径可视为等于地球半径,假设正确,不符合题意;
C.由于山的高度远小于地球的半径,则该卫星的轨道半径可视为等于地球半径,则该卫星为近地卫星,而只有地球同步卫星的周期才等于地球自转的周期,假设错误,符合题意。
故选:。
由于山的高度远小于地球的半径,则该卫星的轨道半径可视为等于地球半径,则该卫星为近地卫星,有,在地球表面有,整理有
。
18.【解析】设地球质量为,在地球表面且忽略地球自转,有
解得。
设卫星质量为,由牛顿第二定律得
联立解得卫星距地球表面的高度。
19. 【解析】 忽略地球自转,万有引力等于重力,即有,
,
得;
以外的球壳对处物体的万有引力为零,设地球总质量为,以内部分地球的总质量为 ,
均匀球体质量,
因此,
重力加速度,
得;
根据以上分析,当离地心的距离小于等于地球半径时,有,
当离地心的距离大于地球半径时,有。
20.【解析】从地球发射飞船到轨道Ⅲ的最小速度即为第一宇宙速度,根据重力提供万有引力,
解得;
当飞船在地球表面静止不动时,有,解得,
设飞船在轨道Ⅰ上的运行速率,轨道Ⅰ是圆轨道,根据万有引力提供向心力,
联立可得;
设飞船在轨道Ⅲ上的运行周期,轨道Ⅲ是圆轨道,根据万有引力提供向心力
又,解得
设飞船在轨道Ⅱ上的运行周期为,轨道半长轴为,根据开普勒第三定律可得,解得
所以飞船在轨道Ⅱ从点到点的时间。
21.【解析】由几何关系知:它们的轨道半径
任意两个星星之间的万有引力
每一颗星星受到的合力是另外两颗星星对它的万有引力的矢量合,由几何关系可知,这两个分力之间的夹角为,根据平行四边形定则可知,,
每一颗星星受到的合力提供其向心力,即:,则;
根据合力提供它们的向心力,则:
可得:;
根据合力提供它们的向心力,则:解得:
可知若等边三角形的边长与每颗星的质量都变成两倍,每颗星的线速度大小不变,即每颗星的线速度大小与之前线速度的比为:。
第16页,共18页
一、单选题
1.与地球公转轨道“外切”的小行星甲和“内切”的小行星乙的公转轨道如图所示,假设这些小行星与地球的公转轨道都在同一平面内,已知地球的公转半径为,公转周期为,小行星甲的远日点到太阳的距离为,小行星乙的近日点到太阳的距离为,引力常量为,下列说法正确的是( )
A. 小行星甲与太阳的连线和小行星乙与太阳的连线在相同时间内扫过的面积相等
B. 小行星乙在远日点的加速度大小等于地球公转的加速度大小
C. 小行星甲的公转周期为
D. 太阳的密度为
2.北京时间年月日时分,搭载神舟十八号载人飞船的长征二号遥十八运载火箭在酒泉卫星发射中心成功发射,日清晨神十八乘组抵达中国空间站。航天员叶光富、李聪、李广苏进入核心舱开展相关工作。已知核心舱的运行轨道距地面高度约为,地球的半径为,地球表面的重力加速度为,引力常量为,忽略地球自转的影响,下列说法正确的是( )
A. 地球的质量可表示为
B. 地球的平均密度可表示为
C. 核心舱的运行速度大小介于和之间
D. 核心舱的运行速度大小为
3.星球上的物体脱离星球引力所需要的最小发射速度称为第二宇宙速度,星球的第二宇宙速度与第一宇宙速度的关系是。已知某星球的半径为,它表面的重力加速度为地球表面重加速度的,不计其他星球的影响,则该星球的第二宇宙速度为( )
A. B. C. D.
4.年月,我国使用长征八号运载火箭将鹊桥二号中继卫星送入近地点高度约、远地点高度约的地月转移轨道,之后鹊桥二号在地面测控支持下,经过中途修正,近月制动进入近月点高度约、远月点高度约、周期为的环月使命轨道Ⅰ,为嫦娥六号月背采样返回任务提供了中继服务。在年,鹊桥二号将调整到近月点高度约、远月点高度约的环月使命轨道Ⅱ,为嫦娥七号、嫦娥八号提供服务。已知地球的半径约为,月球的半径约为,下列说法正确的是( )
A. 根据题目信息可以估算出地球的质量
B. 根据题目信息可以估算出地球的密度
C. 根据题目信息可以估算出鹊桥二号在环月使命轨道Ⅱ上的周期
D. 根据题目信息无法估算出鹊桥二号在环月使命轨道Ⅰ上近月点与远月点的速度大小之比
5.我国计划在年前实现中国载人登月。设想登月载人飞船的运行轨迹如图所示。飞船在圆形“停泊轨道”的点加速进入椭圆“过渡轨道”,该轨道离地球表面最近距离为,飞船到达离点最远距离为的点时,被月球引力“俘获”后,在距月球表面的圆形“绕月轨道”上飞行。已知地球半径为,月球半径为,地球表面重力加速度为,月球表面重力加速度为地球表面重力加速度的,飞船在“过渡轨道”运行时忽略月球引力影响。下列说法正确的是( )
A. 飞船的发射速度必须大于
B. 飞船在“过渡轨道”上点加速度大于“停泊轨道”上点的加速度
C. 飞船在“过渡轨道”上的点运行速度为
D. 飞船从点运动到点的时间为
6.年月日时分,我国神舟十八号载人飞船采用自主快速交会对接模式,成功对接于中国空间站天和核心舱径向端口如图所示,随后名航天员从神舟十八号载人飞船进入中国空间站开展为期六个月的太空工作与生活,这次太空远航,航天员们携带了一个叫做“小受控型生态生命模块”的装置及相关物品进入太空,其中的主要水生生命体就是斑马鱼和金鱼藻,实现我国在外太空培养脊椎动物的首次突破。已知空间站绕地球运行的轨道半径为,地球半径为,地球表面的重力加速度为。则以下判断中正确的是( )
A. 空间站绕地球稳定飞行时,斑马鱼受到万有引力和浮力作用
B. 空间站绕地球飞行速度大于第一宇宙速度
C. 空间站运行的速度大小为
D. 质量为的金鱼藻在空间站所受万有引力的大小为
7.神舟十八号名航天员在轨驻留天,期间进行了次出舱活动,刷新了中国航天员单次出舱活动时间纪录。可近似认为天宫空间站在距离地面高度约为的圆轨道上做匀速圆周运动,地球半径为,不考虑地球自转,地表重力加速度取,出舱活动期间,航天员相对天宫空间站处于静止状态。下列说法正确的是
A. 出舱活动期间,航天员受到的合外力为
B. 空间站运行速度大小约为
C. 空间站运行的向心加速度大小约为
D. 返回舱与天宫空间站分离后,返回地球需要点火加速
8.如图所示,卫星没有发射,停放在地球的赤道上随地球自转;卫星发射成功,在地球赤道上空贴着地表做匀速圆周运动;两卫星的质量相等.认为重力近似等于万有引力.下列说法正确的是( )
A. 、做匀速圆周运动所需的向心力大小相等
B. 做匀速圆周运动的向心加速度等于重力加速度
C. 、做匀速圆周运动的线速度大小相等,都等于第一宇宙速度
D. 做匀速圆周运动的周期大于地球同步卫星的周期
9.我国科研人员利用“探测卫星”获取了某一未知星球的探测数据,如图所示,图线表示“探测卫星”绕该星球运动的关系图像,表示“探测卫星”绕地球运动的关系图像,其中是卫星绕中心天体运动的轨道半径,是对应的周期。“探测卫星”在该星球近表面和地球近表面运动时均满足,图中、、已知,则( )
A. 该星球和地球的质量之比为
B. 该星球和地球的第一宇宙速度之比为
C. 该星球和地球的密度之比为
D. 该星球和地球表面的重力加速度大小之比为
10.甲同学在北极以某一初速度竖直上抛一个小球,经过一段时间落回手中;乙同学在赤道以相同速度竖直上抛另一小球,经过另一段时间落回手中。已知甲、乙抛出小球对应的运动时间的比值为,不考虑空气阻力,则地球第一宇宙速度与地球同步卫星的线速度之比为( )
A. B. C. D.
11.我国成功将“高分十三号”卫星发射升空并顺利进入地球同步轨道。“高分十三号”卫星是一颗高轨光学遥感卫星,可为国民经济发展提供信息服务。研究表明,地球自转在逐渐变慢,亿年前地球自转的周期约为小时。假设这种趋势会持续下去,地球的其他条件都不变。则( )
A. 未来地球的第一宇宙速度小于
B. 未来赤道的重力加速度将逐渐变大
C. 未来极地的重力加速度将逐渐变小
D. 未来人类发射的地球同步卫星与“高分十三号”卫星相比轨道半径将变小
二、多选题
12.在地球表面,被轻质细线悬挂而处于静止状态的质量为的小球,所受地球的万有引力作用效果分解示意图如图所示,已知小球所处的纬度为,重力为,万有引力为,地球的半径为,自转周期为,下列说法正确的是( )
A. 细线的拉力与的合力提供了小球做圆周运动的向心力
B. 小球所需的向心力为
C. 地球赤道处的重力加速度为
D. 地球的第一宇宙速度为
13.土星是太阳系中的第二大行星,距离地球约亿千米如图所示为发射土星探测器的简易图,探测器经地土转移轨道后,经停泊轨道、,最后到达探测轨道已知土星的半径约为地球半径的倍,质量约为地球质量的倍,地球表面的重力加速度大小为,下列说法正确的是( )
A. 探测器的发射速度一定大于
B. 土星表面的重力加速度大小为
C. 探测器在轨道、、的运行周期关系为
D. 探测器在轨道经点的速度小于轨道经点的速度
14.如图所示,飞船在离地球表面高处的轨道上做周期为的匀速圆周运动,已知地球的半径,则:( )
A. 飞船在该轨道上运行的线速度大于第一宇宙速度
B. 飞船在该轨道上运行的线速度大小为
C. 飞船在该轨道上运行时的向心加速度大小为
D. 地球表面的重力加速度大小可表示为
15.如图所示,飞行器绕半径为的某行星做匀速圆周运动,星球相对飞行器的张角为,其环绕周期为,引力常量为,行星可视为质量均匀分布的球体,不考虑行星的自转,下列说法正确的是( )
A. 行量的质量为 B. 行星的平均密度为
C. 行星表面的重力加速度为 D. 行星的第一宇宙速度为
三、实验题
16.月地检验
检验目的:检验地球绕太阳运动、月球绕地球运动的力与地球对树上苹果的引力是否为_______________的力。
检验方法:
假设地球与月球间的作用力和太阳与行星间的作用力是同一种力,它们的表达式也应该满足。
根据牛顿第二定律,月球绕地球做圆周运动的向心加速度式中地是地球质量,是地球中心与月球中心的距离。
假设地球对苹果的吸引力也是同一种力,同理可知,苹果的自由落体加速度式中地是地球的质量,是地球中心与苹果间的距离。
,由于,所以。
验证:
苹果自由落体加速度苹
月球中心到地球中心的距离。
月球公转周期
则月___________保留两位有效数字____________数值比例。
结论:地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力遵从_________________的规律。
17.年月日下午,“天宫课堂”第二课在中国空间站开讲,王亚平做了太空抛物实验,奥运顶流“冰墩墩”在空间站上被航天员抛出后,并没有像在地面上那样做曲线运动,而是水平飞出去了。
请根据此实验回答以下问题:
关于冰墩墩被水平抛出后,做水平运动的原因,以下解释中正确的是_________;
A.冰墩墩在空间站内不受力的作用
B.冰墩墩水平方向不受外力作用
C.冰墩墩处于完全失重的状态
D.冰墩墩随空间站绕地球做匀速圆周运动,万有引力提供向心力
历史上,牛顿曾提出:若在地球表面的高山上来做平抛实验,把物体抛出,它将落向地面;如果将物体抛出的速度变大,它将会落向更远的地方。如果抛出的速度足够大,它有可能不落回地面,而是绕地球运转。已知地球半径为,小伟同学用如下方法推导这一速度:
其结果与正确值相差很远,这是由于他在近似处理中,错误的假设是_________;
A.卫星的轨道是圆的 卫星的轨道半径等于地球半径
C.卫星的周期等于地球自转的周期 卫星的向心力等于它在地球上受到的地球引力
已知地球表面重力加速度,请你利用已学习的物理知识求出正确的“足够大的速度”为_________。保留位有效数字
四、计算题
18.年月日,我国文昌卫星发射中心成功将中星卫星发射升空.若卫星在距地球表面某高度处绕地球做匀速圆周运动的周期为,已知地球表面的重力加速度为,地球可视为均匀球体,其半径为,引力常量为,忽略地球自转影响.求:
地球的质量;
卫星距地球表面的高度.
19.如图所示,假定地球为密度均匀分布的球体,忽略地球的自转,已知地球的半径为。理论和实验证明:质量均匀分布的球壳对壳内物体的万有引力为零。求:
地面上方高的山顶处和地面处重力加速度大小之比
地面下方深的矿井底处和地面处重力加速度大小之比
根据上述两问的结论,定性做出重力加速度随离地心的距离而变化的函数关系式上图中为地球半径,为地球表面处的重力加速度。
20.如图,已知地球半径为,地球表面的重力加速度为,不考虑地球自转的影响,飞船先在近地轨道Ⅲ上绕地球做圆周运动,到达轨道Ⅲ的点时点火变轨进入椭圆轨道Ⅱ,到达轨道Ⅱ的远地点时再次点火进入轨道Ⅰ绕地球做圆周运动,轨道Ⅰ的轨道半径为,求:
从地球发射飞船到轨道Ⅲ的最小速度
飞船在轨道Ⅰ上的运行速率
飞船在轨道Ⅱ从点到点的时间.
21.宇宙间存在一些离其他恒星较远的三星系统,其中一种三星系统如图所示。三颗质量均为的星体位于等边三角形的三个顶点,三角形边长为。忽略其他星体对它们的引力作用,三星在同一平面内绕三角形中心做匀速圆周运动,万有引力常量为,,
求每颗星的加速度大小;
每颗星做匀速圆周运动的周期;
若等边三角形的边长与每颗星的质量都变成两倍,则每颗星的线速度大小与之前线速度的比。
答案和解析
1.【答案】
【解析】A.根据开普勒第二定律可知,同一行星与太阳的连线在相同时间内扫过的面积相等,但小行星甲与小行星乙在不同轨道上,所以小行星甲与太阳的连线和小行星乙与太阳的连线在相同时间内扫过的面积不相等,故A错误;
B.根据牛顿第二定律可得
可得
由于小行星乙在远日点离太阳距离等于地球离太阳距离,则小行星乙在远日点的加速度大小等于地球公转的加速度大小,故B正确;
C.根据开普勒第三定律可得
解得小行星甲的公转周期为
故C错误;
D.设太阳质量为 ,太阳半径为 ,太阳的密度为 ,则有
地球绕太阳转动,由万有引力提供向心力可得
联立可得太阳的密度为
故D错误。
故选B。
2.【答案】
【解析】A.设地球的质量为,不考虑地球自转的影响,地面上质量为的物体所受的重力等于地球对物体的引力,即,解得:,故A错误;
B.地球的平均密度为,故B错误;
C.第一宇宙速度为最大的环绕速度,核心舱的运行速度小于第一字宙速度,即小于,故C错误;
D.核心舱所受万有引力提供向心力有:,结合,解得,故D正确。
3.【答案】
【解析】解:在星球表面,重力等于其表面卫星的环绕速度,根据牛顿第二定律,有:
解得:
根据题意,有:
故
故选:
4.【答案】
【解析】设鹊桥二号在地月转移轨道上的近地点的高度为,远地点的高度为,地球的直径为,鹊桥二号的运行周期为,根据开普勒第三定律可得
根据牛顿第二定律和万有引力定律
则
解得
由于引力常量与周期未知,故地球的质量和密度无法求得,故AB错误;
C.设环月使命轨道Ⅰ的近月点高度为,远月点高度为,环月使命轨道Ⅱ的近月点高度为,远月点高度为,月球的直径为,题目中已知鹊桥二号在环月使命轨道上的周期为,根据开普勒第三定律,可以求得鹊桥二号在环月使命轨道Ⅱ上的周期为,故C正确;
D.设鹊桥二号在环月使命轨道Ⅰ上近月点与远月点的速度大小分别为和,近月点到月心的距离,远月点到月心的距离,根据开普勒第二定律,解得,故D错误。
5.【答案】
【解析】A、飞船运动中未脱离地球引力的束缚,其发射速度大于第一宇宙速度而小于第二宇宙速度,地球的第二宇宙速度为,则飞船的发射速度一定小于,故A错误;
B、由知,飞船在“过渡轨道”上点加速度等于“停泊轨道”上点的加速度,故B错误;
C、由卫星变轨知,飞船在“过渡轨道”上的点运行速度大于其在停泊轨道上运动的速度,题设条件不足,无法计算出飞船在“过渡轨道”上的点运行速度,故C错误;
D、飞船在停泊轨道运动时,由牛顿第二定律:,在地球表面:,由开普勒第三定律:,联立知,飞船从点运动到点的时间为,故D正确。
6.【答案】
【解析】空间站绕地球稳定飞行时,万有引力提供向心力,处于完全失重状态,所以斑马鱼只受万有引力作用,不受浮力作用,A错误
地球第一宇宙速度是卫星绕地球做匀速圆周运动的最大线速度,可知空间站绕地飞行速度小于第一宇宙速度,B错误
根据万有引力与重力的关系有,根据万有引力提供向心力有,解得空间站的速度大小为,C错误
质量为的金鱼藻在空间站所受万有引力的大小为,根据万有引力与重力的关系得,解得,D正确。
7.【答案】
【解析】解析: 出舱活动期间,航天员做绕地球的匀速圆周运动,受到的合外力提供向心力,受到的合外力不为, 故A错误
地球对空间站的万有引力提供空间站做匀速圆周运动需要的向心力,可得: , 又因为在地球表面有: ,联立两式可得: ,第一宇宙速度 可知B错误 , ,故C正确
返回舱与天宫空间站分离后,返回地球时,根据变轨规律知,需要点火减速,故 D错误.
8.【答案】
【解析】A、两卫星的质量相等,到地心的距离相等,所以受到地球的万有引力相等.卫星在赤道上随地球自转而做圆周运动,万有引力的一部分提供自转的向心力,卫星在赤道上空贴着地表做匀速圆周运动,万有引力全部用来提供公转的向心力,因此、做匀速圆周运动所需的向心力大小不相等,项错误;
B、对卫星,重力近似等于万有引力,万有引力全部用来提供向心力,所以向心加速度等于重力加速度,项正确;
C、卫星在赤道上空贴着地表做匀速圆周运动,其速度就是最大的环绕速度,也是第一宇宙速度,卫星在赤道上随地球自转而做圆周运动,向心力小于卫星的向心力,根据牛顿第二定律,卫星的线速度小于的线速度,即的线速度小于第一宇宙速度,项错误;
D、在赤道上随地球自转而做圆周运动,自转周期等于地球的自转周期,同步卫星的周期也等于地球的自转周期,所以做匀速圆周运动的周期等于地球同步卫星的周期,项错误.
故选B。
9.【答案】
【解析】A.根据万有引力提供向心力有,解得,可知图像的斜率为,故该星球和地球的质量之比,故A错误;
B.“探测卫星”在该星球近表面和地球近表面运动时均满足,即,可得,根据万有引力提供向心力有,解得,故该星球和地球的第一宇宙速度之比,故B正确;
C.星球的体积为,密度为,故该星球和地球的密度之比为,故C错误;
D.在星球表面,万有引力与重力的关系有,解得,故该星球和地球表面的重力加速度大小之比为,故D错误。
10.【答案】
【解析】设小球的初速度为,在北极小球运动的时间为,重力加速度为在赤道小球运动的时间为,重力加速度为,由竖直上抛,可得,,则
设地球半径为,在北极,
在赤道,,为地球自转周期。
设地球第一宇宙速度大小为,同步卫星的线速度大小为,周期与地球自转周期相等也为,
由,
同步卫星,,
联立以上各式解得,A正确。
11.【答案】
【解析】A、地球半径为,质量为,根据可得,可见第一宇宙速度与地球自转周期无关,而且第一宇宙速度是,不是,故A错误;
、在赤道上有,在两极有,
地球自转在逐渐变慢,即自转周期变大,则未来赤道的重力加速度将逐渐变大,极地的重力加速度不变,故B正确,C错误;
D、根据,可得同步卫星轨道半径,变大,则轨道半径变大,故D错误。
故选B。
12.【答案】
【解析】A.细线的拉力 与的合力提供了小球做圆周运动的向心力,故A正确;
B.小球做圆周运动的半径为 ,所以小球所需的向心力为
故B错误;
C.小球所处的纬度重力为 大于赤道处的重力,所以地球赤道处的重力加速度小于 ,故C错误;
D.根据 可得地球的第一宇宙速度为
故D正确。
13.【答案】
【解析】探测器需要到达土星,因此最终会脱离地球的引力束缚,但还在太阳系中,故发射速度应大于,小于,A错误
由万有引力等于重力,有,解得,故土星表面的重力加速度大小,B正确
由开普勒第三定律,有,可知轨道的半长轴最大、轨道的轨道半径最小,所以探测器在轨道、、的运行周期关系为,C正确
探测器在轨道上经过点后做离心运动,有,探测器在轨道上经过点做匀速圆周运动,有,故,D错误.
14.【答案】
【解析】、研究飞船绕地球做匀速圆周运动,根据万有引力提供向心力,列出等式:
,其中为地球质量,为轨道半径,
飞船在离地球表面 高处的轨道上做周期为的匀速圆周运动,飞船的轨道半径,
第一宇宙速度是近地卫星的环绕速度,也是最大的圆周运动的环绕速度,所以飞船运行的线速度小于第一宇宙速度,故A错误.
B、根据圆周运动知识得:运行的线速度大小,故B正确.
C、根据圆周运动知识得:运行时的向心加速度大小,故C正确.
D、,得:
忽略地球自转的影响,在地球表面根据万有引力等于重力列出等式:
由得:地球表面的重力加速度大小故D错误。
15.【答案】
【解析】由题意可得,M=ρ 4/3 πr^3,故选:。
16.【答案】同一性质 相同
【解析】月地检验的目的就是检验地球绕太阳运动、月球绕地球运动的力与地球对树上苹果的引力是否是同一种性质的力。
已知,
已知,。
先计算的值:,。则保留两位有效数字。
已知,,
则。
通过月地检验,计算出的的值与理论推导相符,说明地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力遵从相同的规律。
17.【答案】;;
【解析】冰墩墩在空间站内受地球等的万有引力作用,故A错误;
冰墩墩随空间站绕地球做匀速圆周运动,万有引力提供向心力,处于完全失重状态,由于万有引力指向地心,则冰墩墩水平方向不受外力作用,故BCD正确;
故选:。
如果抛出的速度足够大,它有可能不落回地面,而是绕地球运转,由万有引力提供向心力,做匀速圆周运动,假设正确,不符合题意;
B.由于山的高度远小于地球的半径,则该卫星的轨道半径可视为等于地球半径,假设正确,不符合题意;
C.由于山的高度远小于地球的半径,则该卫星的轨道半径可视为等于地球半径,则该卫星为近地卫星,而只有地球同步卫星的周期才等于地球自转的周期,假设错误,符合题意。
故选:。
由于山的高度远小于地球的半径,则该卫星的轨道半径可视为等于地球半径,则该卫星为近地卫星,有,在地球表面有,整理有
。
18.【解析】设地球质量为,在地球表面且忽略地球自转,有
解得。
设卫星质量为,由牛顿第二定律得
联立解得卫星距地球表面的高度。
19. 【解析】 忽略地球自转,万有引力等于重力,即有,
,
得;
以外的球壳对处物体的万有引力为零,设地球总质量为,以内部分地球的总质量为 ,
均匀球体质量,
因此,
重力加速度,
得;
根据以上分析,当离地心的距离小于等于地球半径时,有,
当离地心的距离大于地球半径时,有。
20.【解析】从地球发射飞船到轨道Ⅲ的最小速度即为第一宇宙速度,根据重力提供万有引力,
解得;
当飞船在地球表面静止不动时,有,解得,
设飞船在轨道Ⅰ上的运行速率,轨道Ⅰ是圆轨道,根据万有引力提供向心力,
联立可得;
设飞船在轨道Ⅲ上的运行周期,轨道Ⅲ是圆轨道,根据万有引力提供向心力
又,解得
设飞船在轨道Ⅱ上的运行周期为,轨道半长轴为,根据开普勒第三定律可得,解得
所以飞船在轨道Ⅱ从点到点的时间。
21.【解析】由几何关系知:它们的轨道半径
任意两个星星之间的万有引力
每一颗星星受到的合力是另外两颗星星对它的万有引力的矢量合,由几何关系可知,这两个分力之间的夹角为,根据平行四边形定则可知,,
每一颗星星受到的合力提供其向心力,即:,则;
根据合力提供它们的向心力,则:
可得:;
根据合力提供它们的向心力,则:解得:
可知若等边三角形的边长与每颗星的质量都变成两倍,每颗星的线速度大小不变,即每颗星的线速度大小与之前线速度的比为:。
第16页,共18页
