第5单元三角形应用题专项训练(含答案)2024-2025学年数学四年级下册人教版
文档属性
| 名称 | 第5单元三角形应用题专项训练(含答案)2024-2025学年数学四年级下册人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 530.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 17:23:03 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第5单元三角形应用题专项训练-2024-2025学年数学四年级下册人教版
1.爷爷给菜地设计篱笆,他想了以下几种方案,哪种方案设计的篱笆最牢固?为什么?
2.用36厘米长的铁丝围成一个等腰三角形,如果这个三角形的底边长是14厘米,那么每条腰长是多少厘米?
3.如图,湖边有A,B,P,Q四个村庄。邮递员从A村送信到B村,总是走经过Q村的道路,不走经过P村的道路,这是为什么呢?
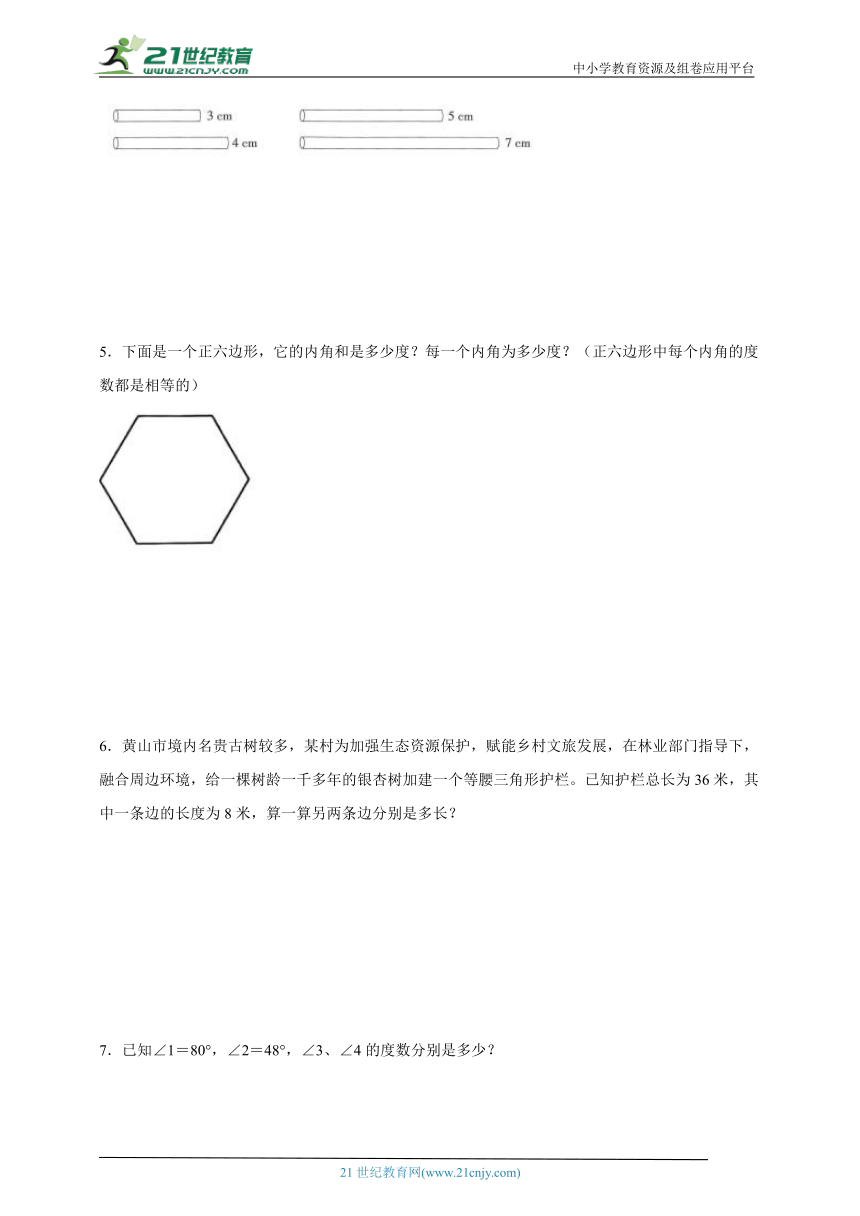
4.如图,有4根长度不等的小棒,任选其中3根小棒围成三角形,可以围成几种不同形状的三角形?
5.下面是一个正六边形,它的内角和是多少度?每一个内角为多少度?(正六边形中每个内角的度数都是相等的)
6.黄山市境内名贵古树较多,某村为加强生态资源保护,赋能乡村文旅发展,在林业部门指导下,融合周边环境,给一棵树龄一千多年的银杏树加建一个等腰三角形护栏。已知护栏总长为36米,其中一条边的长度为8米,算一算另两条边分别是多长?
7.已知∠1=80°,∠2=48°,∠3、∠4的度数分别是多少?
8.2024“珠海 ‘筝’有你的”香洲区第六届风筝会于5月1日~5月2日在香炉湾沙滩举行。各式风筝表演惊艳亮相。淘淘也参与了此次活动,他做了一个等腰三角形的风筝。
(1)如果风筝的周长是32分米,底边是8分米,那么这个风筝的一条腰长多少分米?
(2)如果这个风筝的一个内角是50°,那么它的另外两个内角分别是多少度?
9.阅读与尝试。我们已经知道了三角形的内角是180°,其实三角形除了内角还有外角。如图,延长三角形ABC的一条边BC到点D,∠4就是三角形的一个外角。我们发现:∠4的度数与三角形内角∠1、∠2的度数之和刚好相等,即∠4=∠1+∠2,请利用所学的数学知识来说明理由。
10.小明不小心把一块三角形的玻璃打成了三片(如下图),现在他要到玻璃店去配一块形状完全相同的玻璃,那么最好的办法是带哪一块去?为什么?
11.一个等腰三角形的一个内角是30°,其他两个内角可能各是多少度?这个三角形按角分类可能是什么三角形?
12.学校举行做风筝比赛,图图做了一个等腰三角形的风筝,它的一个底角是30°。这个风筝的顶角是多少度?
13.爷爷用篱笆围成了一个长是40分米,宽是20分米的长方形菜地,如果改围成一个腰长35分米的等腰三角形菜地(篱笆无剩余),这个等腰三角形菜地的底边长多少分米?
14.小军用一根铁丝围成了一个边长是16厘米的等边三角形。如果用这根铁丝围成一个正方形,这个正方形面积是多少?
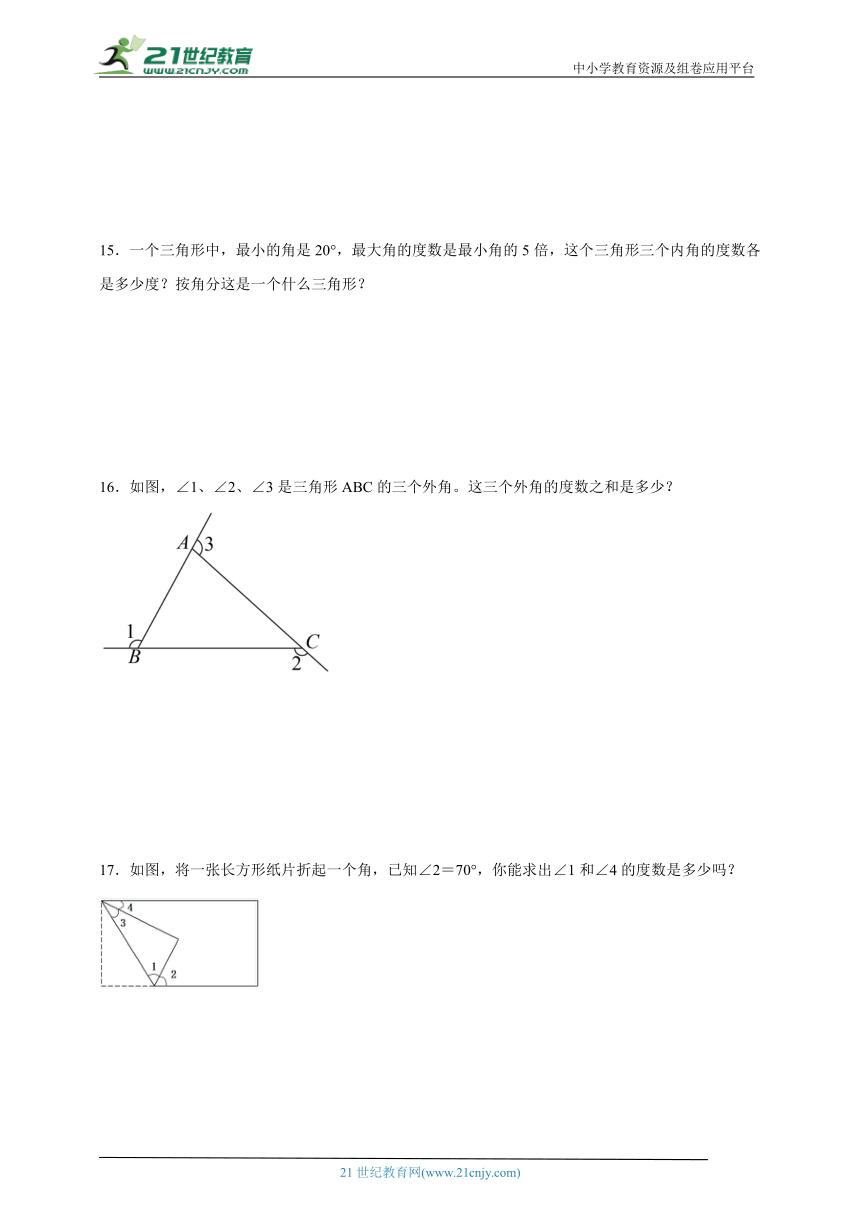
15.一个三角形中,最小的角是20°,最大角的度数是最小角的5倍,这个三角形三个内角的度数各是多少度?按角分这是一个什么三角形?
16.如图,∠1、∠2、∠3是三角形ABC的三个外角。这三个外角的度数之和是多少?
17.如图,将一张长方形纸片折起一个角,已知∠2=70°,你能求出∠1和∠4的度数是多少吗?
18.下图长方体的前后两个面都是正方形,其中A点是边的中点。三角形ABC是一个什么三角形?用你觉得合适的方法说明。(说明思考过程)
19.用一根铁丝可以围成一个边长是18cm的正方形。如果用这根铁丝围成一个腰长是23cm的等腰三角形,则这个等腰三角形的底边长多少厘米?
20.把一个用一根铁丝围成的边长为6分米的正方形拆开,围成一个底边长为10分米的等腰三角形,每条腰长多少分米?
21.如图,一块三角形玻璃被打碎了一个角,这个角是多少度?按边分,这个三角形是什么三角形?
22.如图,已知∠1=65°,∠2=25°,∠3=55°。求∠5的度数。
23.埃及金字塔的四个侧面的形状都是等腰三角形,每个等腰三角形的顶角约是52°。金字塔每个侧面的底角大约是多少度?
24.五角星“☆”具有“胜利”的含义,常出现在军衔标志上。
(1)观察如表,并将表格补充完整。
正多边形 多边形内角和 每个角的度数
正三角形 180° 60°
正方形 360° 90°
正五边形
(2)根据正五边形每个内角的度数,你能推导出图1中∠1的度数吗?
(3)图2是一个标准的五角星,那么∠1+∠2+∠3+∠4+∠5=( )°。
《第5单元三角形应用题专项训练-2024-2025学年数学四年级下册人教版》参考答案
1.②;理由见详解
【分析】三角形具有稳定性,有着稳固、坚定、耐压的特点,埃及金字塔、钢轨、三角形框架、起重机、三角形吊臂、屋顶、三角形钢架、钢架桥和埃菲尔铁塔都以三角形形状建造;四边形具有易变形的特性,即不稳定性,升降机、晾衣架等都利用了平行四边形的这种特性。据此解答。
【详解】答:方案②设计的篱笆最牢靠。方案①和方案③篱笆中间的形状是长方形或者平行四边形,它们都易变形。而方案②篱笆中间的形状是三角形,三角形具有稳定性,所以方案②设计的篱笆最牢靠。
2.11厘米
【分析】等腰三角形的两条腰相等,据此用周长减去底边长求出两条腰的和,再除以2即可求解。
【详解】(36-14)÷2
=22÷2
=11(厘米)
答:每条腰长时11厘米。
3.见详解
【分析】如下图,延长AQ交线段 PB于点E,根据三角形两边之和大于第三边,在三角形APE中,AP+PE>AE,在三角形BEQ中,QE+EB>BQ ,所以AP+PE+QE+EB>AQ+QE+BQ, 即AP+PB>AQ+BQ,据此解答。
【详解】AP+PE>AE
QE+EB>BQ
所以AP+PE+QE+EB>AE+BQ
AP+PB+QE>AQ+QE+BQ
AP+PB>AQ+BQ
走经过Q村的道路比走经过P村的道路距离更短,所以邮递员从A 村送信到B村,总是走经过Q村的道路,不走经过P村的道路。
4.3种
【分析】根据题意,三角形三条边的关系:任意两边的长度和大于第三边,任意两边的长度差小于第三边;据此判断即可。
【详解】根据分析可知:
第一种:3+4>5,5-3<4,3厘米、4厘米、5厘米围成三角形。
第二种:3+5>7,7-3<5,3厘米、5厘米、7厘米围成三角形。
第三种:4+5>7,7-4<5,4厘米、5厘米、7厘米围成三角形。
答:可以围成3种不同形状的三角形。
5.720°;120°
【分析】
三角形的内角和是180°,正六边形可以分成4个三角形,求正六边形的内角和就用180°×4,据此求出正六边形的内角和。正六边形中每个内角的度数都是相等的,所以每个内角的度数=内角和÷6,据此解题。
【详解】180°×4=720°
720°÷6=120°
答:它的内角和是720°,每一个内角为120°。
6.14米;14米
【分析】等腰三角形的两条边相等。由题意得,等腰三角形护栏的总长为36米,其中一条边的长度为8米,可以假设这条边为腰或底边,然后算出剩下的边的长度。最后再根据三角形三边的关系:任意两边之和大于第三边(较短两边之和大于第三边)来验证该假设是否成立即可。
【详解】假设8米的边为腰,那么另一条腰的长度也为8米。
36-8×2
=36-16
=20(米)
8+8=16(米),16米<20米,即这三边无法围成三角形。
假设8米的边为底
(36-8)÷2
=28÷2
=14(米),即两条腰的长度都是14米。
8+14=22(米),22米>14米,即这三边可以围成三角形。
答:剩下的两条边都是14米。
7.∠3=52°;∠4=128°
【分析】三角形的内角和是180°,利用180°减去∠1和∠2的度数即可求出∠3的度数,∠3和∠4合起来是一个180°的平角,利用180°减去∠3的度数就是∠4的度数。
【详解】∠3=180°-80°-48°
=100°-48°
=52°
∠4=180°-52°=128°
答:∠3的度数是52°,∠4的度数是128°。
8.(1)12分米
(2)50°和80°或两个65°
【分析】(1)三角形周长等于3条边之和,根据等腰三角形的特征,风筝的周长是32分米,底边是8分米,那么这个风筝的一条腰长是(32-8)÷2=12(分米),据此解答即可。
(2)根据等腰三角形的特征,可以假设这个内角分别为底角和顶角,再依据三角形的内角和是180度和等腰三角形的底角相等的特点,即可分别计算出两种情况下其他内角的度数。
【详解】(1)(32-8)÷2
=24÷2
=12(分米)
答:这个风筝的一条腰长是12分米。
(2)假设这个内角是底角,则另一个底角也是50°。
顶角为:
180°-50°×2
=180°-100°
=80°
假设这个内角是顶角,每个底角的度数为:
(180°-50°)÷2
=130°÷2
=65°
答:它的另外两个内角分别是50°和80°或两个65°。
9.因为,,所以
【分析】三角形的内角和等于180°,平角等于180°,据此解答。
【详解】根据题意可知,
所以,也就是三角形的一个外角∠4的度数等于与它不相邻的两个内角∠1、∠2的度数之和。
10.第③块;理由见详解
【分析】三角形的内角和为180°。知道三角形2个内角的度数,直接用180°减去两个内角的度数即可算出第三个角的度数;由题意得,第①块玻璃中,只有原来三角形玻璃的一个角,无法确定原来三角形的形状。第②块玻璃中,没有原来三角形玻璃的角,也无法确定原来三角形的形状。第③块玻璃中,有原来三角形玻璃的两个角,延长残缺的两条边即可得到三角形玻璃的第三个角。
【详解】答:最好的办法是带第③块玻璃去。因为直接延长第③块玻璃残缺的两条边即可得到原来三角形玻璃的形状,而其余两块玻璃无法得到原来三角形的形状。
11.角是顶角,其他两个内角是75°;锐角三角形
角是底角时,顶角为120°;钝角三角形
【分析】 等腰三角形是指至少有两边相等的三角形 ,两腰的夹角称为 顶角,腰和底边的夹角称为底角,等腰三角形的两个底角度数相等。三个角都是锐角的三角形是锐角三角形;有一个角是直角的三角形是直角三角形;有一个角是钝角的三角形是钝角三角形。根据三角形的内角和等于180°,当30°是顶角时,两个底角为(180°-30°)÷2=75°,这个三角形按角分是锐角三角形;当30°是底角时,另一个底角也是30°,顶角为180°-30°-30°=120°,这个三角形按角分是钝角三角形,据此解答即可。
【详解】当30°是顶角时:
(180°-30°)÷2
=150°÷2
=75°
其余两个内角分别是75°和75°。这个三角形按角分是锐角三角形。
当30°是底角时:
180°-30°-30°
=150°-30°
=120°
其余两个内角分别是30°和120°。这个三角形按角分是钝角三角形。
12.120°
【分析】等腰三角形的两个底角相等。三角形的内角和是180°。据此解答。
已知一个底角是30°,那么两个底角的度数和为。
所以顶角的度数列式为。
【详解】
答:这个风筝的顶角是120°。
13.50分米
【分析】根据题意可知:篱笆的长度就是长方形菜地和等腰三角形菜地的周长;先根据长方形的周长=(长+宽)×2,求出长方形菜地的周长,也就是等腰三角形菜地的周长,因为等腰三角形两腰相等,所以有两条边的长度是35分米 ,再用周长减去2个35分米,即得到等腰三角形菜地的底边长。据此解答。
【详解】长方形的周长:(40+20)×2
=60×2
=120(分米)
三角形的底:120-35×2
=120-70
=50(分米)
答:这个等腰三角形菜地的底边长50分米。
14.144平方厘米
【分析】由题可知,小军用一根铁丝围成了一个边长是16厘米的等边三角形,如果用这根铁丝围成一个正方形,则三角形的周长等于正方形的周长;根据等边三角形三边相等的特征,求出三角形的周长(即这根铁丝的长度),也就是正方形的周长,用正方形的周长÷4,求出正方形的边长;最后根据正方形的面积=边长×边长,即可求出这个正方形的面积;据此解答即可。
【详解】16×3=48(厘米)
48÷4=12(厘米)
12×12=144(平方厘米)
答:这个正方形的面积是144平方厘米。
15.20°、60°、100°;钝角三角形
【分析】最小角的度数乘5等于最大角的度数,180°减最小角和最大角的度数等于第三个角的度数,三个角都是锐角的三角形是锐角三角形,有一个角是直角的三角形是直角三角形,有一个角是钝角的三角形是钝角三角形,据此即可解答。
【详解】20°×5=100°
180°-20°-100°
=160°-100°
=60°
三角形中最大角等于100°,是钝角,所以三角形是钝角三角形。
答:三角形角三个内角分别是20°、60°、100°,按角分这是一个钝角三角形。
16.360°
【分析】根据三角形的内角和是180°,平角是180°,先求出∠1、∠2、∠3、∠4、∠5、∠6六个角的度数和;然后,用度数和减去∠4、∠5、∠6的和,即可求出三个外角的度数之和。
【详解】
因为平角是180°,
所以,,;
所以∠1、∠2、∠3、∠4、∠5、∠6六个角的度数和是:
因为三角形的内角和是180°,
所以∠1、∠2、∠3三个角的度数和是180°;
答:这三个外角的度数之和是360°。
17.∠1是55°;∠4是20°
【分析】平角是180°,∠1=(180°-∠2)÷2;∠3和∠1所在的三角形是直角三角形,直角90°,∠3=90°-∠1,∠4=90°-∠3-∠3。
【详解】(180°-70°)÷2
=110°÷2
=55°
90°-55°=35°
90°-35°-35°=20°
答:∠1是55°,∠4是20°。
18.
等腰直角三角形;理由见详解
【分析】长方体的前后两个面都是正方形,并且A点是边的中点,则AD=BD=AE=EC,那么三角形ADB与三角形ACE是完全一样的等腰直角三角形,所以∠DAB=∠EAC=45°,则∠BAC=平角-45°×2=90°,有一个角是直角两腰相等的三角形是等腰直角三角形。
【详解】
180°-45°×2
=80°-90°
=90°
答:三角形ABC是等腰直角三角形。
19.26厘米
【分析】根据正方形的周长=边长×4,求出这根铁丝的长度,再根据等腰三角形的特征,等腰三角形的两条腰的长度相等,用这根铁丝的长度减去两腰的长度,就是底边的长度,据此作答。
【详解】铁丝的长度:18×4=72(厘米)
72-23×2
=72-46
=26(厘米)
答:这个等腰三角形的底边长26厘米。
20.7分米
【分析】把一个用一根铁丝围成的边长为6分米的正方形,据此根据正方形的周长=边长×4,先算出这根铁丝的长度;当用这根铁丝围成一个等腰三角形时,等腰三角形的周长就是这根铁丝的长度;已知这个三角形的底边长是10分米,根据等腰三角形的两腰长度相等,可知等腰三角形的腰长=(等腰三角形的周长-底边的长)÷2,代入数据,即可求出等腰三角形的腰长。据此列式计算即可。
【详解】6×4=24(分米)
(24-10)÷2
=14÷2
=7(分米)
答:每条腰长7分米。
21.60°;等边三角形
【分析】三角形内角和等于180°,180°减去两个已知角的度数等于打碎角的度数,再根据三个角的度数判断三条边的关系,根据三条边的相互关系判断是什么三角形,据此即可解答。
【详解】180°-60°-60°
=120°-60°
=60°
三个角都是60°,所以三条边都相等,按边分,这个三角形是等边三角形。
答:打碎的这个角是60°,按边分,这个三角形是等边三角形。
22.35°
【分析】根据三角形内角和为180°,∠2和∠3还有一个角组成一个三角形,用180°-∠2-∠3先求出这个角的度数,根据题意可知,这个角与∠4组成平角,则用180°减去这个角的度数即可求出∠4的度数,再根据∠1和∠4还有∠5组成三角形,用180°-∠1-∠4,即可求出∠5的度数。
【详解】180°-∠2-∠3=180°-25°-55°=155°-55°=100°;
∠4=180°-100°=80°;
∠5=180°-∠1-∠4=180°-65°-80°=115°-80°=35°。
答:∠5=35°。
23.64度
【分析】等腰三角形的特征:两腰相等,两底角也相等;再根据三角形内角和是180°和一个顶角是52°,先求得两个底角的度数,进而求得它的一个底角的度数。
【详解】180°-52°=128°
128°÷2=64°
答:金字塔每个侧面的底角大约是64度。
【点睛】此题根据等腰三角形的特征和三角形的内角和解决。
24.(1)540°;108°;
(2)36°;
(3)180°
【分析】(1)多边形的内角和=(多边形的边数-2)×180°,正五边形有5条边,5条边的长度相等,且5个内角也相等,依此计算。
(2)标准的五角星中,每条边的长度都相等,因此∠1所在的小三角形是等腰三角形,等腰三角形的两个底角相等,1平角是180°,因此用180°减正五边形其中一个内角的度数,即可计算出∠6的度数,三角形的内角和是180°,因此用180°减2个∠6的度数即可,依此计算。
(3)由(2)可知,一个标准的五角星的每个角都是36°,所以∠1+∠2+∠3+∠4+∠5的和为5个36°,依此计算。
【详解】(1)(5-2)×180°
=3×180°
=540°
540°÷5=108°,即填表如下:
正多边形 多边形内角和 每个角的度数
正三角形 180° 60°
正方形 360° 90°
正五边形 540° 108°
(2)180°-108°=72°
180°-72°-72°=36°
答:图1中∠1的度数是36°。
(3)∠1+∠2+∠3+∠4+∠5
=36°+36°+36°+36°+36°
=180°
【点睛】解答此题的关键是要熟练掌握多边形的内角和的计算方法,以及应掌握平角的特点。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第5单元三角形应用题专项训练-2024-2025学年数学四年级下册人教版
1.爷爷给菜地设计篱笆,他想了以下几种方案,哪种方案设计的篱笆最牢固?为什么?
2.用36厘米长的铁丝围成一个等腰三角形,如果这个三角形的底边长是14厘米,那么每条腰长是多少厘米?
3.如图,湖边有A,B,P,Q四个村庄。邮递员从A村送信到B村,总是走经过Q村的道路,不走经过P村的道路,这是为什么呢?
4.如图,有4根长度不等的小棒,任选其中3根小棒围成三角形,可以围成几种不同形状的三角形?
5.下面是一个正六边形,它的内角和是多少度?每一个内角为多少度?(正六边形中每个内角的度数都是相等的)
6.黄山市境内名贵古树较多,某村为加强生态资源保护,赋能乡村文旅发展,在林业部门指导下,融合周边环境,给一棵树龄一千多年的银杏树加建一个等腰三角形护栏。已知护栏总长为36米,其中一条边的长度为8米,算一算另两条边分别是多长?
7.已知∠1=80°,∠2=48°,∠3、∠4的度数分别是多少?
8.2024“珠海 ‘筝’有你的”香洲区第六届风筝会于5月1日~5月2日在香炉湾沙滩举行。各式风筝表演惊艳亮相。淘淘也参与了此次活动,他做了一个等腰三角形的风筝。
(1)如果风筝的周长是32分米,底边是8分米,那么这个风筝的一条腰长多少分米?
(2)如果这个风筝的一个内角是50°,那么它的另外两个内角分别是多少度?
9.阅读与尝试。我们已经知道了三角形的内角是180°,其实三角形除了内角还有外角。如图,延长三角形ABC的一条边BC到点D,∠4就是三角形的一个外角。我们发现:∠4的度数与三角形内角∠1、∠2的度数之和刚好相等,即∠4=∠1+∠2,请利用所学的数学知识来说明理由。
10.小明不小心把一块三角形的玻璃打成了三片(如下图),现在他要到玻璃店去配一块形状完全相同的玻璃,那么最好的办法是带哪一块去?为什么?
11.一个等腰三角形的一个内角是30°,其他两个内角可能各是多少度?这个三角形按角分类可能是什么三角形?
12.学校举行做风筝比赛,图图做了一个等腰三角形的风筝,它的一个底角是30°。这个风筝的顶角是多少度?
13.爷爷用篱笆围成了一个长是40分米,宽是20分米的长方形菜地,如果改围成一个腰长35分米的等腰三角形菜地(篱笆无剩余),这个等腰三角形菜地的底边长多少分米?
14.小军用一根铁丝围成了一个边长是16厘米的等边三角形。如果用这根铁丝围成一个正方形,这个正方形面积是多少?
15.一个三角形中,最小的角是20°,最大角的度数是最小角的5倍,这个三角形三个内角的度数各是多少度?按角分这是一个什么三角形?
16.如图,∠1、∠2、∠3是三角形ABC的三个外角。这三个外角的度数之和是多少?
17.如图,将一张长方形纸片折起一个角,已知∠2=70°,你能求出∠1和∠4的度数是多少吗?
18.下图长方体的前后两个面都是正方形,其中A点是边的中点。三角形ABC是一个什么三角形?用你觉得合适的方法说明。(说明思考过程)
19.用一根铁丝可以围成一个边长是18cm的正方形。如果用这根铁丝围成一个腰长是23cm的等腰三角形,则这个等腰三角形的底边长多少厘米?
20.把一个用一根铁丝围成的边长为6分米的正方形拆开,围成一个底边长为10分米的等腰三角形,每条腰长多少分米?
21.如图,一块三角形玻璃被打碎了一个角,这个角是多少度?按边分,这个三角形是什么三角形?
22.如图,已知∠1=65°,∠2=25°,∠3=55°。求∠5的度数。
23.埃及金字塔的四个侧面的形状都是等腰三角形,每个等腰三角形的顶角约是52°。金字塔每个侧面的底角大约是多少度?
24.五角星“☆”具有“胜利”的含义,常出现在军衔标志上。
(1)观察如表,并将表格补充完整。
正多边形 多边形内角和 每个角的度数
正三角形 180° 60°
正方形 360° 90°
正五边形
(2)根据正五边形每个内角的度数,你能推导出图1中∠1的度数吗?
(3)图2是一个标准的五角星,那么∠1+∠2+∠3+∠4+∠5=( )°。
《第5单元三角形应用题专项训练-2024-2025学年数学四年级下册人教版》参考答案
1.②;理由见详解
【分析】三角形具有稳定性,有着稳固、坚定、耐压的特点,埃及金字塔、钢轨、三角形框架、起重机、三角形吊臂、屋顶、三角形钢架、钢架桥和埃菲尔铁塔都以三角形形状建造;四边形具有易变形的特性,即不稳定性,升降机、晾衣架等都利用了平行四边形的这种特性。据此解答。
【详解】答:方案②设计的篱笆最牢靠。方案①和方案③篱笆中间的形状是长方形或者平行四边形,它们都易变形。而方案②篱笆中间的形状是三角形,三角形具有稳定性,所以方案②设计的篱笆最牢靠。
2.11厘米
【分析】等腰三角形的两条腰相等,据此用周长减去底边长求出两条腰的和,再除以2即可求解。
【详解】(36-14)÷2
=22÷2
=11(厘米)
答:每条腰长时11厘米。
3.见详解
【分析】如下图,延长AQ交线段 PB于点E,根据三角形两边之和大于第三边,在三角形APE中,AP+PE>AE,在三角形BEQ中,QE+EB>BQ ,所以AP+PE+QE+EB>AQ+QE+BQ, 即AP+PB>AQ+BQ,据此解答。
【详解】AP+PE>AE
QE+EB>BQ
所以AP+PE+QE+EB>AE+BQ
AP+PB+QE>AQ+QE+BQ
AP+PB>AQ+BQ
走经过Q村的道路比走经过P村的道路距离更短,所以邮递员从A 村送信到B村,总是走经过Q村的道路,不走经过P村的道路。
4.3种
【分析】根据题意,三角形三条边的关系:任意两边的长度和大于第三边,任意两边的长度差小于第三边;据此判断即可。
【详解】根据分析可知:
第一种:3+4>5,5-3<4,3厘米、4厘米、5厘米围成三角形。
第二种:3+5>7,7-3<5,3厘米、5厘米、7厘米围成三角形。
第三种:4+5>7,7-4<5,4厘米、5厘米、7厘米围成三角形。
答:可以围成3种不同形状的三角形。
5.720°;120°
【分析】
三角形的内角和是180°,正六边形可以分成4个三角形,求正六边形的内角和就用180°×4,据此求出正六边形的内角和。正六边形中每个内角的度数都是相等的,所以每个内角的度数=内角和÷6,据此解题。
【详解】180°×4=720°
720°÷6=120°
答:它的内角和是720°,每一个内角为120°。
6.14米;14米
【分析】等腰三角形的两条边相等。由题意得,等腰三角形护栏的总长为36米,其中一条边的长度为8米,可以假设这条边为腰或底边,然后算出剩下的边的长度。最后再根据三角形三边的关系:任意两边之和大于第三边(较短两边之和大于第三边)来验证该假设是否成立即可。
【详解】假设8米的边为腰,那么另一条腰的长度也为8米。
36-8×2
=36-16
=20(米)
8+8=16(米),16米<20米,即这三边无法围成三角形。
假设8米的边为底
(36-8)÷2
=28÷2
=14(米),即两条腰的长度都是14米。
8+14=22(米),22米>14米,即这三边可以围成三角形。
答:剩下的两条边都是14米。
7.∠3=52°;∠4=128°
【分析】三角形的内角和是180°,利用180°减去∠1和∠2的度数即可求出∠3的度数,∠3和∠4合起来是一个180°的平角,利用180°减去∠3的度数就是∠4的度数。
【详解】∠3=180°-80°-48°
=100°-48°
=52°
∠4=180°-52°=128°
答:∠3的度数是52°,∠4的度数是128°。
8.(1)12分米
(2)50°和80°或两个65°
【分析】(1)三角形周长等于3条边之和,根据等腰三角形的特征,风筝的周长是32分米,底边是8分米,那么这个风筝的一条腰长是(32-8)÷2=12(分米),据此解答即可。
(2)根据等腰三角形的特征,可以假设这个内角分别为底角和顶角,再依据三角形的内角和是180度和等腰三角形的底角相等的特点,即可分别计算出两种情况下其他内角的度数。
【详解】(1)(32-8)÷2
=24÷2
=12(分米)
答:这个风筝的一条腰长是12分米。
(2)假设这个内角是底角,则另一个底角也是50°。
顶角为:
180°-50°×2
=180°-100°
=80°
假设这个内角是顶角,每个底角的度数为:
(180°-50°)÷2
=130°÷2
=65°
答:它的另外两个内角分别是50°和80°或两个65°。
9.因为,,所以
【分析】三角形的内角和等于180°,平角等于180°,据此解答。
【详解】根据题意可知,
所以,也就是三角形的一个外角∠4的度数等于与它不相邻的两个内角∠1、∠2的度数之和。
10.第③块;理由见详解
【分析】三角形的内角和为180°。知道三角形2个内角的度数,直接用180°减去两个内角的度数即可算出第三个角的度数;由题意得,第①块玻璃中,只有原来三角形玻璃的一个角,无法确定原来三角形的形状。第②块玻璃中,没有原来三角形玻璃的角,也无法确定原来三角形的形状。第③块玻璃中,有原来三角形玻璃的两个角,延长残缺的两条边即可得到三角形玻璃的第三个角。
【详解】答:最好的办法是带第③块玻璃去。因为直接延长第③块玻璃残缺的两条边即可得到原来三角形玻璃的形状,而其余两块玻璃无法得到原来三角形的形状。
11.角是顶角,其他两个内角是75°;锐角三角形
角是底角时,顶角为120°;钝角三角形
【分析】 等腰三角形是指至少有两边相等的三角形 ,两腰的夹角称为 顶角,腰和底边的夹角称为底角,等腰三角形的两个底角度数相等。三个角都是锐角的三角形是锐角三角形;有一个角是直角的三角形是直角三角形;有一个角是钝角的三角形是钝角三角形。根据三角形的内角和等于180°,当30°是顶角时,两个底角为(180°-30°)÷2=75°,这个三角形按角分是锐角三角形;当30°是底角时,另一个底角也是30°,顶角为180°-30°-30°=120°,这个三角形按角分是钝角三角形,据此解答即可。
【详解】当30°是顶角时:
(180°-30°)÷2
=150°÷2
=75°
其余两个内角分别是75°和75°。这个三角形按角分是锐角三角形。
当30°是底角时:
180°-30°-30°
=150°-30°
=120°
其余两个内角分别是30°和120°。这个三角形按角分是钝角三角形。
12.120°
【分析】等腰三角形的两个底角相等。三角形的内角和是180°。据此解答。
已知一个底角是30°,那么两个底角的度数和为。
所以顶角的度数列式为。
【详解】
答:这个风筝的顶角是120°。
13.50分米
【分析】根据题意可知:篱笆的长度就是长方形菜地和等腰三角形菜地的周长;先根据长方形的周长=(长+宽)×2,求出长方形菜地的周长,也就是等腰三角形菜地的周长,因为等腰三角形两腰相等,所以有两条边的长度是35分米 ,再用周长减去2个35分米,即得到等腰三角形菜地的底边长。据此解答。
【详解】长方形的周长:(40+20)×2
=60×2
=120(分米)
三角形的底:120-35×2
=120-70
=50(分米)
答:这个等腰三角形菜地的底边长50分米。
14.144平方厘米
【分析】由题可知,小军用一根铁丝围成了一个边长是16厘米的等边三角形,如果用这根铁丝围成一个正方形,则三角形的周长等于正方形的周长;根据等边三角形三边相等的特征,求出三角形的周长(即这根铁丝的长度),也就是正方形的周长,用正方形的周长÷4,求出正方形的边长;最后根据正方形的面积=边长×边长,即可求出这个正方形的面积;据此解答即可。
【详解】16×3=48(厘米)
48÷4=12(厘米)
12×12=144(平方厘米)
答:这个正方形的面积是144平方厘米。
15.20°、60°、100°;钝角三角形
【分析】最小角的度数乘5等于最大角的度数,180°减最小角和最大角的度数等于第三个角的度数,三个角都是锐角的三角形是锐角三角形,有一个角是直角的三角形是直角三角形,有一个角是钝角的三角形是钝角三角形,据此即可解答。
【详解】20°×5=100°
180°-20°-100°
=160°-100°
=60°
三角形中最大角等于100°,是钝角,所以三角形是钝角三角形。
答:三角形角三个内角分别是20°、60°、100°,按角分这是一个钝角三角形。
16.360°
【分析】根据三角形的内角和是180°,平角是180°,先求出∠1、∠2、∠3、∠4、∠5、∠6六个角的度数和;然后,用度数和减去∠4、∠5、∠6的和,即可求出三个外角的度数之和。
【详解】
因为平角是180°,
所以,,;
所以∠1、∠2、∠3、∠4、∠5、∠6六个角的度数和是:
因为三角形的内角和是180°,
所以∠1、∠2、∠3三个角的度数和是180°;
答:这三个外角的度数之和是360°。
17.∠1是55°;∠4是20°
【分析】平角是180°,∠1=(180°-∠2)÷2;∠3和∠1所在的三角形是直角三角形,直角90°,∠3=90°-∠1,∠4=90°-∠3-∠3。
【详解】(180°-70°)÷2
=110°÷2
=55°
90°-55°=35°
90°-35°-35°=20°
答:∠1是55°,∠4是20°。
18.
等腰直角三角形;理由见详解
【分析】长方体的前后两个面都是正方形,并且A点是边的中点,则AD=BD=AE=EC,那么三角形ADB与三角形ACE是完全一样的等腰直角三角形,所以∠DAB=∠EAC=45°,则∠BAC=平角-45°×2=90°,有一个角是直角两腰相等的三角形是等腰直角三角形。
【详解】
180°-45°×2
=80°-90°
=90°
答:三角形ABC是等腰直角三角形。
19.26厘米
【分析】根据正方形的周长=边长×4,求出这根铁丝的长度,再根据等腰三角形的特征,等腰三角形的两条腰的长度相等,用这根铁丝的长度减去两腰的长度,就是底边的长度,据此作答。
【详解】铁丝的长度:18×4=72(厘米)
72-23×2
=72-46
=26(厘米)
答:这个等腰三角形的底边长26厘米。
20.7分米
【分析】把一个用一根铁丝围成的边长为6分米的正方形,据此根据正方形的周长=边长×4,先算出这根铁丝的长度;当用这根铁丝围成一个等腰三角形时,等腰三角形的周长就是这根铁丝的长度;已知这个三角形的底边长是10分米,根据等腰三角形的两腰长度相等,可知等腰三角形的腰长=(等腰三角形的周长-底边的长)÷2,代入数据,即可求出等腰三角形的腰长。据此列式计算即可。
【详解】6×4=24(分米)
(24-10)÷2
=14÷2
=7(分米)
答:每条腰长7分米。
21.60°;等边三角形
【分析】三角形内角和等于180°,180°减去两个已知角的度数等于打碎角的度数,再根据三个角的度数判断三条边的关系,根据三条边的相互关系判断是什么三角形,据此即可解答。
【详解】180°-60°-60°
=120°-60°
=60°
三个角都是60°,所以三条边都相等,按边分,这个三角形是等边三角形。
答:打碎的这个角是60°,按边分,这个三角形是等边三角形。
22.35°
【分析】根据三角形内角和为180°,∠2和∠3还有一个角组成一个三角形,用180°-∠2-∠3先求出这个角的度数,根据题意可知,这个角与∠4组成平角,则用180°减去这个角的度数即可求出∠4的度数,再根据∠1和∠4还有∠5组成三角形,用180°-∠1-∠4,即可求出∠5的度数。
【详解】180°-∠2-∠3=180°-25°-55°=155°-55°=100°;
∠4=180°-100°=80°;
∠5=180°-∠1-∠4=180°-65°-80°=115°-80°=35°。
答:∠5=35°。
23.64度
【分析】等腰三角形的特征:两腰相等,两底角也相等;再根据三角形内角和是180°和一个顶角是52°,先求得两个底角的度数,进而求得它的一个底角的度数。
【详解】180°-52°=128°
128°÷2=64°
答:金字塔每个侧面的底角大约是64度。
【点睛】此题根据等腰三角形的特征和三角形的内角和解决。
24.(1)540°;108°;
(2)36°;
(3)180°
【分析】(1)多边形的内角和=(多边形的边数-2)×180°,正五边形有5条边,5条边的长度相等,且5个内角也相等,依此计算。
(2)标准的五角星中,每条边的长度都相等,因此∠1所在的小三角形是等腰三角形,等腰三角形的两个底角相等,1平角是180°,因此用180°减正五边形其中一个内角的度数,即可计算出∠6的度数,三角形的内角和是180°,因此用180°减2个∠6的度数即可,依此计算。
(3)由(2)可知,一个标准的五角星的每个角都是36°,所以∠1+∠2+∠3+∠4+∠5的和为5个36°,依此计算。
【详解】(1)(5-2)×180°
=3×180°
=540°
540°÷5=108°,即填表如下:
正多边形 多边形内角和 每个角的度数
正三角形 180° 60°
正方形 360° 90°
正五边形 540° 108°
(2)180°-108°=72°
180°-72°-72°=36°
答:图1中∠1的度数是36°。
(3)∠1+∠2+∠3+∠4+∠5
=36°+36°+36°+36°+36°
=180°
【点睛】解答此题的关键是要熟练掌握多边形的内角和的计算方法,以及应掌握平角的特点。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
