人教版必修二第六章 圆周运动(含解析)
文档属性
| 名称 | 人教版必修二第六章 圆周运动(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-04-21 17:26:46 | ||
图片预览




文档简介
第六章圆周运动
一、单选题
1.如图所示,摩天轮悬挂的座舱在竖直平面内做匀速圆周运动已知座舱的质量为,运动半径为,角速度大小为,重力加速度为,则座舱( )
A. 运动的周期为
B. 线速度大小为
C. 运动至圆心等高处时,所受摩天轮的作用力大于
D. 运动至最低点时,所受摩天轮的作用力大小与最高点的相等
2.如图所示是天工开物中牛力齿轮的图画及其原理简化图,牛拉动横杆驱动半径为的大齿轮匀速率转动,大齿轮与半径为的中齿轮垂直咬合,中齿轮通过横轴与半径为小齿轮相连,小齿轮驱动抽水桶抽水,已知牛拉横杆转一圈需要时间为,则抽水桶的运动速率约为( )
A. B. C. D.
3.如图所示,半径为的鼓形轮可绕固定的光滑水平轴转动。在轮上沿相互垂直的直径方向固定四根直杆,杆上分别固定有质量为的、、、个小球,球心与的距离均为。现让鼓形轮匀速转动,若某时刻,两球所在直杆恰好位于水平方向,小球的速度大小为,不计空气阻力,重力加速度为,下列说法正确的是( )
A. 鼓形轮的角速度为 B. 杆对小球的作用力一定竖直向上
C. 杆对小球的作用力为 D. 杆对小球的作用力一定大于
4.如图所示,摩天轮悬挂的座舱在竖直平面内做匀速圆周运动.座舱的质量为,运动的半径为,角速度大小为,重力加速度为,则座舱( )
A. 运动周期为
B. 线速度的大小为
C. 受摩天轮作用力的大小始终为
D. 运动至圆心等高处时,受摩天轮作用力大于
5.骑自行车是一种绿色环保的出行方式。如图所示是某款自行车传动结构的示意图,该自行车的大齿轮、小齿轮与后轮的半径之比为,它们的边缘分别有,,三个点,则下列说法正确的是
A. ,两点的周期之比为 B. ,两点的角速度之比为
C. ,两点的线速度大小之比为 D. ,两点的向心加速度大小之比为
6.两个质量不同的小球用长度不等的细线栓在同一点并在同一水平面内做匀速圆周运动,则它们的( )
A. 角速度相同 B. 线速度大小相同
C. 周期不同 D. 向心加速度大小相同
7.光滑直杆可绕竖直轴转动,质量为的小球套在杆上。现先让直杆绕轴以角速度匀速转动,,稳定后小球在图示位置,此时小球的加速度大小为,速度大小为;增大为,再让直杆以角速度匀速转动,稳定后小球的高度不变,此时小球的加速度大小为,速度大小为。则
A. ,, B. ,,
C. ,, D. ,,
8.如图所示,两个相同材料制成的靠摩擦转动的轮和轮水平放置两轮不打滑,两轮半径。当主动轮匀速转动时,在轮边缘上放置的小木块恰能相对静止。若将小木块放在轮上,欲使小木块相对轮静止,则木块距轮转轴的最大距离为 ( )
A. B. C. D.
9.如图所示,支架固定在底座上,它们的总质量为。质量分别为和的小球、可视为质点固定在一根长度为的轻杆两端,该轻杆通过光滑转轴安装在支架的横梁上,、间的距离为,两小球和轻杆一起绕轴在竖直平面内做圆周运动,运动过程中支架和底座一直保持静止。当转动到图示竖直位置时,小球的速度为,重力加速度为。对于该位置,下列说法正确的是( )
A. 小球、的向心加速度大小相等
B. 小球的向心力大于球的向心力
C. 若,则底座对水平地面的压力为
D. A、两球恰好做匀速圆周运动
10.如图所示,竖直平面内有一“”型光滑细杆,杆与水平面间夹角均为,杆上套有形状相同质量不同的小球、,现让杆绕底部点所在的竖直轴匀速转动,下列说法不正确的是( )
A. 两球的角速度大小相同
B. 两球的向心加速度大小不同
C. 两球始终处于同一高度
D. 若杆瞬间停止转动,则停转后两球的加速度大小相等
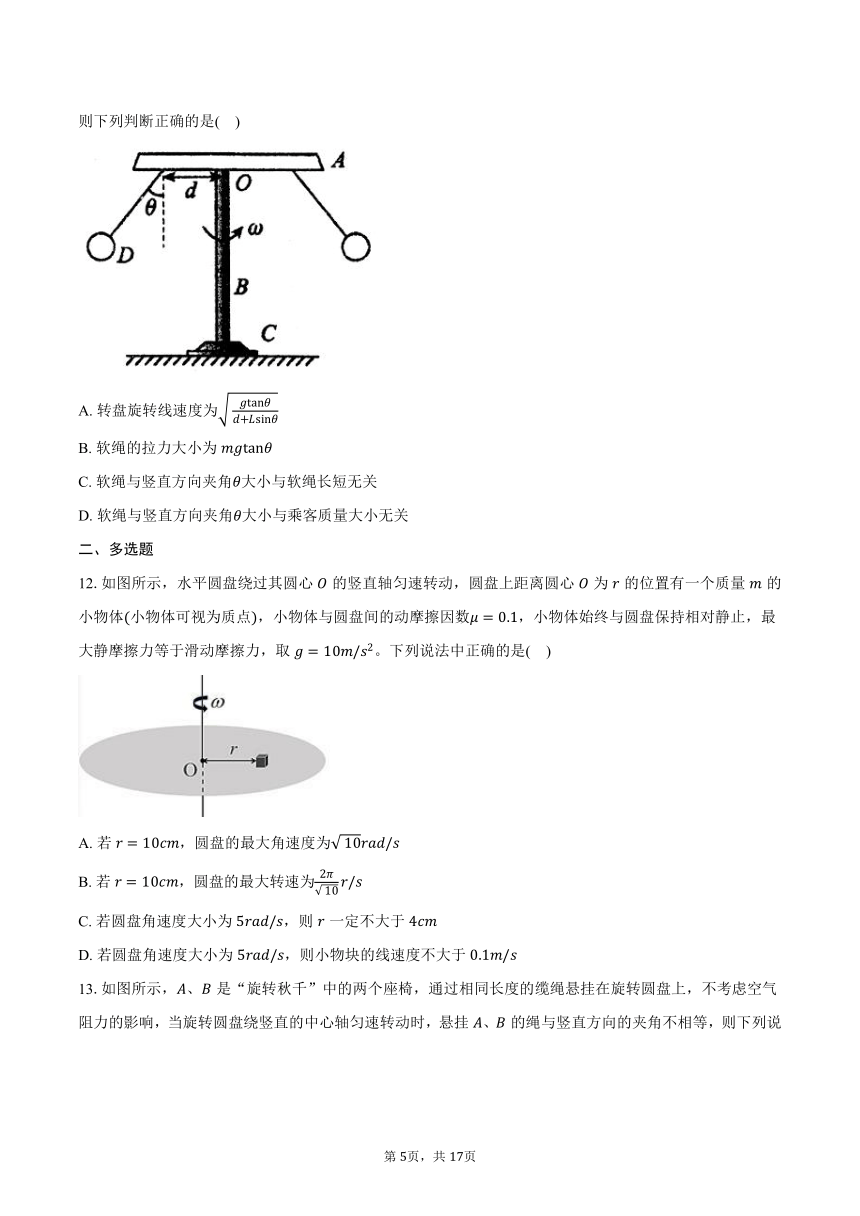
11.如图为某游乐园飓风飞椅结构简图其装置由伞型转盘、中间圆柱、底座和软绳悬挂飞椅可视为质点组成,在距转盘下表面轴心距离为的圆周上,用软绳分布均匀地悬挂座飞椅,飞椅与人的质量之和均为,悬挂飞椅的绳长均为,当水平转盘以角速度稳定旋转时,各软绳与竖直方向成角。则下列判断正确的是( )
A. 转盘旋转线速度为
B. 软绳的拉力大小为
C. 软绳与竖直方向夹角大小与软绳长短无关
D. 软绳与竖直方向夹角大小与乘客质量大小无关
二、多选题
12.如图所示,水平圆盘绕过其圆心的竖直轴匀速转动,圆盘上距离圆心为的位置有一个质量的小物体小物体可视为质点,小物体与圆盘间的动摩擦因数,小物体始终与圆盘保持相对静止,最大静摩擦力等于滑动摩擦力,取。下列说法中正确的是( )
A. 若,圆盘的最大角速度为
B. 若,圆盘的最大转速为
C. 若圆盘角速度大小为,则一定不大于
D. 若圆盘角速度大小为,则小物块的线速度不大于
13.如图所示,、是“旋转秋千”中的两个座椅,通过相同长度的缆绳悬挂在旋转圆盘上,不考虑空气阻力的影响,当旋转圆盘绕竖直的中心轴匀速转动时,悬挂、的绳与竖直方向的夹角不相等,则下列说法正确的是( )
A. 的速度比的速度大 B. 与的向心加速度大小相等
C. 的转动半径小于的转动半径 D. 与的转动周期相等
14.如图所示,长为的悬线固定在点,在点正下方有一钉子,长为,把悬线另一端的小球拉到跟悬点在同一水平面上无初速度地释放,小球运动到悬点正下方时悬线碰到钉子的瞬间 ( )
A. 小球的线速度突然增大为原来的倍
B. 小球的角速度突然增大为原来的倍
C. 小球的向心力突然增大为原来的倍
D. 小球的所受悬线的拉力突然增大为原来的倍
15.某学校的机动车出入口采用如图所示的曲杆道闸,道闸由转动杆与横杆链接而成,、为横杆的两个端点。某天中午快递员将快递袋子挂在了校门口道闸的横杆上,由于门卫没有及时将快递袋取下,在道闸抬起过程中,快递袋始终与横杆保持相对静止,且杆始终水平,此过程中杆绕点从水平方向匀速转动到接近竖直方向。若快递袋可视为质点,与横杆之间的动摩擦因数为,最大静摩擦力等于滑动摩擦力,转动杆长度为,重力加速度为。下列说法正确的是( )
A. 、两点的加速度不同
B. 点的加速度始终沿方向
C. 、两点都在做匀速圆周运动
D. 快递袋能够与横杆保持相对静止一起运动的最大速率
三、实验题
16.如图所示,某兴趣小组利用电动机驱动轻杆带动小球做竖直面内的匀速圆周运动,改变小球质量,通过力传感器获得轻杆拉力最大值随小球质量变化的关系,并求得当地的重力加速度。
为了测得当地的重力加速度,至少还应该知道________填选项序号。
A.小球做圆周运动的周期 小球做圆周运动的半径 力传感器的质量
采用图像法处理数据时,应该作出________填“”或者“”图像,若图像斜率为,当地的重力加速度________用和中已知量表示。
17.某兴趣小组的同学设计了图所示的装置,用来测量滑块质量滑块可视为质点和滑块与水平台面间的动摩擦因数。水平转台能绕竖直的轴匀速转动,装有遮光条的小滑块放置在转台上,不可伸长的细线一端连接小滑块,另一端连到固定在转轴上的力传感器上,连接到计算机上的传感器能显示细线的拉力,安装在铁架台上的光电门可以读出遮光条通过光电门的挡光时间,兴趣小组采取了下列步骤:
用游标卡尺测量遮光条的宽度;
将滑块放置在转台上,使细线刚好绷直,量出滑块到转轴的距离;
控制转台以某一角速度匀速转动,记录力传感器和光电门的示数,分别为和;依次增大转台的角速度,并保证其每次都做匀速转动,记录对应的力传感器示数、和光电门的示数、。回答下面的问题:
滑块匀速转动的线速度可表示为______用、中字母表示。
如图,当大于时,滑块做匀速圆周运动的向心力由哪些力提供( )
A.绳子的拉力 转盘的摩擦力 绳子的拉力和转盘的摩擦力
处理数据时,兴趣小组的同学以力传感器的示数为纵轴,为横轴,建立直角坐标系,描点后拟合为一条直线,如图所示图中、已知,设最大静摩擦力等于滑动摩擦力,重力加速度为,则物块的质量______,动摩擦因数______。用、、、中字母表示
四、计算题
18.如图所示,半径为的半球形陶罐,固定在可以绕竖直轴旋转的水平转台上,转台转轴与过陶罐球心的对称轴重合,转台以一定角速度匀速旋转.一质量为的小物块落入陶罐内,经过一段时间后,小物块随陶罐一起转动且相对罐壁静止,它和点的连线与之间的夹角为重力加速度大小为.
求出物块线速度大小;
若时,小物块受到的摩擦力恰好为零,求;
若为第问的值,且,求小物块受到的摩擦力大小;
19.一种离心测速器的简化工作原理如图所示。细杆的一端固定在竖直转轴上的点,并可随轴一起转动。杆上套有一轻质弹簧,弹簧一端固定于点,另一端与套在杆上的圆环相连。当测速器稳定工作时,圆环将相对细杆静止,通过圆环的位置可以确定细杆匀速转动的角速度。已知细杆长度,杆与竖直转轴的夹角始终为,弹簧原长,弹簧劲度系数,圆环质量;弹簧始终在弹性限度内,摩擦力可忽略不计
若细杆和圆环处于静止状态,求圆环到点的距离;
求弹簧处于原长时,细杆匀速转动的角速度大小;
求圆环处于细杆末端时,细杆匀速转动的角速度大小。
20.如图所示,半径为的水平圆盘距地面的高度,质量均的、两个物块,均可看成质点,用一根不可伸长的轻绳连在一起,轻绳经过圆盘圆心,、两物块的转动半径,在转盘边缘。和一起随圆盘绕竖直中心轴转动为转盘圆心在地面沿竖直方向的投影,转动角速度从零开始缓慢增大,直到有物块相对圆盘运动为止。它们与圆盘间的动摩擦因数均为。取最大静摩擦力等于滑动摩擦力,不计空气阻力,重力加速度为,求:
当绳上恰好出现拉力时,圆盘的角速度大小;
绳上出现拉力后,随着角速度的缓慢增加,是否有物体受到的摩擦力为零?如果有,求出此时圆盘角速度大小;
若水平圆盘距地面的高度为,随着角速度进一步缓慢增加,两物块相对圆盘滑动,假设滑动瞬间绳子断裂,求落地的位置与之间的距离。
答案和解析
1.
【解析】由,可知AB错误;
C.运动至圆心等高处时,所受摩天轮的作用力,故C正确;
D.由座舱做匀速圆周运动,可知座舱所受的合力提供向心力,,方向始终指向摩天轮中心,则座舱在最低点时,其所受摩天轮的作用力为,最高点时,其所受摩天轮的作用力为,故D错误。
2.
【解析】半径为的大齿轮匀速率转动,大齿轮与半径为的中齿轮垂直咬合,二者线速度相等,,中齿轮通过横轴与半径为小齿轮相连,二者角速度相等,抽水桶的运动速率,故A项正确。
3.
【解析】A. 鼓形轮的角速度为,故A错误;
B. 小球所需的向心力大小为
若,则杆对小球的作用力竖直向下,故B错误;
C. 对小球,竖直方向有
水平方向有
则杆对小球的作用力为,故C错误;
D. 对小球,根据牛顿第二定律可得
可知杆对小球的作用力一定大于,故D正确。
故选D。
4.
【解析】A、根据角速度和周期的关系可知,周期,故A错误;
B、根据线速度与角速度的关系可得,线速度大小,故B错误;
C、座舱做匀速圆周运动,其向心力由重力和摩天轮对座舱的作用力的合力提供,根据牛顿第二定律,这里是合力并非摩天轮对座舱的作用力,故 C错误;
D、当座舱运动至与圆心等高位置时,向心力由摩天轮对座舱的作用力的水平分力提供,竖直方向上摩天轮对座舱的作用力的竖直分力与重力平衡,即。根据力的合成,此时摩天轮对座舱的作用力,显然,所以选项正确。
5.
【解析】A.由 , ,可得,故A错误;
B.、两点为同轴转动,角速度相等,,由得周期相等,,可得,故B错误;
C.由,得,故C正确;
D.由,可得,故D错误。
6.
【解析】对其中一个小球受力分析,如图
受重力,绳子的拉力,由于小球做匀速圆周运动,故重力和拉力合力提供向心力,由几何关系和向心力公式得
设绳子与悬挂点间的高度差为,由几何关系,得
联立得
则角速度与绳子的长度和转动半径无关,根据 可得周期相同,A正确、C错误;
B.由 ,可知线速度与做圆周运动半径成正比,但两球做圆周运动半径不同,则线速度大小不相同,B错误;
D.两球的角速度相同,但两球做圆周运动半径不等,由 得,两球向心加速度不等,D错误。
故选A。
7.
【解析】设圆周运动所在平面与的高度为,圆周半径为,则,
,解上式得:,所以线速度与角度、半径无关,因此。
由于圆周半径为根据,,可知,,故B正确ACD错误。
8.
【解析】和用相同材料制成的靠摩擦传动,边缘线速度相同,则
而。
所以
对于在边缘的木块,最大静摩擦力恰为向心力,即
当在轮上恰要滑动时,设此时半径为
则
解得
故ABD错误,C正确。
故选C。
9.
【解析】A.两小球和轻杆一起绕轴在竖直平面内做圆周运动,所以两小球的角速度相同,根据可知小球、的加速度之比为::,故A错误;
B.根据可知、的向心力之比为::,故B错误;
C.若,对分析则有,解得轻杆对支持力为,根据可知,对分析则有,解得轻杆对拉力为,以底座和轻杆为对象,水平地面对底座的支持力为,所以底座对水平地面的压力为,故C错误;
D. 由分析知向心力之比为::,故两球恰好做匀速圆周运动,故D正确;
10.
【解析】A.让杆绕底部点所在的竖直轴匀速转动,两个小球同轴转动,角速度相等,故A正确,不合题意;
分析小球受力可知:,,则,所以两球圆周运动的半径相等,始终处于同一高度;
向心加速度:,相等,故B错误,符合题意,C正确,不合题意;
D.若杆瞬间停止转动,停转后,分析小球受力可知:,,则小球加速度,所以两球的加速度大小相等,故D正确,不合题意。
故选B。
11.
【解析】A.如图所示,对质点受力分析,由牛顿第二定律可得:,根据几何关系可得:,解得转盘旋转角速度为,故A错误;
B.绳中的拉力,故B错误;
根据:,软绳与竖直方向夹角大小只与转速和软绳长短有关,与乘客质量无关,故D正确,C错误。
故选D。
12.
【解析】小物体始终与圆盘保持相对静止,所以静摩擦力提供向心力,即。
当摩擦力等于最大静摩擦力时,角速度达到最大、转速达到最大。
即,若,,转速,故A正确、B错误;
由的分析可知,。若圆盘角速度大小为,则
由可知,,故C正确、D错误。
13.
【解析】解:设坐椅的悬挂点到转轴的距离为,绳长为。对座椅受力分析如图:
C、两个座椅具有相同的角速度,由牛顿第二定律可知,结合题意可得,的转动半径小于的转动半径,故C正确;
A、两个座椅具有相同的角速度,根据公式,的转动半径小于的半径,则的线速度小于的线速度,故A错误;
B、根据公式,的转动半径小于的半径,两个座椅具有相同的角速度,则的向心加速度小于的向心加速度,故B错误;
D、根据公式,两个座椅具有相同的角速度,故A与的转动周期相等,故D正确。
故选:。
14.
【解析】A.悬线与钉子碰撞前后,线的拉力始终与小球运动方向垂直,小球的线速度不变。故A错误;
B.当半径减小时,由变大为原来的倍,故B正确;
C.由知向心力突然增大为原来的倍,故C正确;
D.而在最低点,故碰到钉子后合力变为原来的倍,悬线拉力变大,但不是原来的倍,故D错误。
故选BC。
15.
【解析】、、两点相对静止,运动状态相同,加速度相同,均做匀速圆周运动,A错误,C正确;
B、由前分析知,点加速度始终和方向平行即和点加速度同向,B错误;
D、设快递袋质量为,做圆周运动时向心加速度和水平方向夹角为,如图:
由,,,
联立得,其中,由数学知识可知,最大值为,D正确。
16.;;。
【解析】最低点时拉力最大,满足,解得,
所以还需要知道小球做匀速圆周运动的周期和半径,
故选AB。
作图像,且图像的斜率,解得。
17.;;;
【解析】滑块匀速转动的线速度 ;
当 小于时,静摩擦力提供向心力,此时拉力为零,当 大于 时,静摩擦力不足以提供向心力,还需要有绳子的拉力,故选C。
对在转台上做匀速圆周运动的滑块,当 大于 时,
由牛顿第二定律有 ,
解得: ,
根据图乙可知
,解得: ,
,解得:.
18.解:转动的线速度:
小物块在水平面内做匀速圆周运动,当小物块受到的摩擦力恰好等于零时,小物块所受的重力和陶罐的支持力的合力提供圆周运动的向心力,
有:
解得:
当时,小物块受到的摩擦力沿陶罐壁切线向下,设摩擦力的大小为,陶罐壁对小物块的支持力为,沿水平和竖直方向建立坐标系,则:
水平方向:
竖直方向:
代入数据解得:
同理,当时,小物块受到的摩擦力沿陶罐壁切线向上,则:
水平方向:
竖直方向:
代入数据解得:。
19.解:静止时对圆环受力分析有:
解得: ;
对圆环有:水平方向:
竖直方向:
解得: ;
圆环处于细杆末端时,对圆环受力分析,受重力,弹簧伸长,弹力沿杆向下。
根据胡克定律得,
根据对圆环受力分析,并正交分解,竖直方向受力平衡,水平方向合力提供向心力,
则有,
由几何关系得,
联立解得。
20.解:绳上恰好出现拉力时,与转盘之间为最大静摩擦力,即最大静摩擦力提供其向心力,则有:
解得圆盘的角速度为: ,即当绳上恰好出现拉力时,圆盘的角速度大小为;
绳上出现拉力后,随着角速度的缓慢增加,此时对物体受力分析有: ,对物体受力分析有: ,联立两式可得:
,可知:随着角速度的缓慢增加,物体收到的摩擦力逐渐减小,当 时,即: ,可得: ;
当圆盘的角速度大于时,此时对物体受力分析有: ,对物体受力分析有:,联立两式可得: ,可知:随着角速度的缓慢增加,物体收到的摩擦力逐渐增大,当物体受到的静摩擦力最大时,两物块即将相对圆盘滑动,即: ,可得: ,此时物体是速度 ,此后物体将做平抛运动,有: , ,联立两式带入数据可得:,由几何关系可知: 落地的位置与之间的距离.
第11页,共17页
一、单选题
1.如图所示,摩天轮悬挂的座舱在竖直平面内做匀速圆周运动已知座舱的质量为,运动半径为,角速度大小为,重力加速度为,则座舱( )
A. 运动的周期为
B. 线速度大小为
C. 运动至圆心等高处时,所受摩天轮的作用力大于
D. 运动至最低点时,所受摩天轮的作用力大小与最高点的相等
2.如图所示是天工开物中牛力齿轮的图画及其原理简化图,牛拉动横杆驱动半径为的大齿轮匀速率转动,大齿轮与半径为的中齿轮垂直咬合,中齿轮通过横轴与半径为小齿轮相连,小齿轮驱动抽水桶抽水,已知牛拉横杆转一圈需要时间为,则抽水桶的运动速率约为( )
A. B. C. D.
3.如图所示,半径为的鼓形轮可绕固定的光滑水平轴转动。在轮上沿相互垂直的直径方向固定四根直杆,杆上分别固定有质量为的、、、个小球,球心与的距离均为。现让鼓形轮匀速转动,若某时刻,两球所在直杆恰好位于水平方向,小球的速度大小为,不计空气阻力,重力加速度为,下列说法正确的是( )
A. 鼓形轮的角速度为 B. 杆对小球的作用力一定竖直向上
C. 杆对小球的作用力为 D. 杆对小球的作用力一定大于
4.如图所示,摩天轮悬挂的座舱在竖直平面内做匀速圆周运动.座舱的质量为,运动的半径为,角速度大小为,重力加速度为,则座舱( )
A. 运动周期为
B. 线速度的大小为
C. 受摩天轮作用力的大小始终为
D. 运动至圆心等高处时,受摩天轮作用力大于
5.骑自行车是一种绿色环保的出行方式。如图所示是某款自行车传动结构的示意图,该自行车的大齿轮、小齿轮与后轮的半径之比为,它们的边缘分别有,,三个点,则下列说法正确的是
A. ,两点的周期之比为 B. ,两点的角速度之比为
C. ,两点的线速度大小之比为 D. ,两点的向心加速度大小之比为
6.两个质量不同的小球用长度不等的细线栓在同一点并在同一水平面内做匀速圆周运动,则它们的( )
A. 角速度相同 B. 线速度大小相同
C. 周期不同 D. 向心加速度大小相同
7.光滑直杆可绕竖直轴转动,质量为的小球套在杆上。现先让直杆绕轴以角速度匀速转动,,稳定后小球在图示位置,此时小球的加速度大小为,速度大小为;增大为,再让直杆以角速度匀速转动,稳定后小球的高度不变,此时小球的加速度大小为,速度大小为。则
A. ,, B. ,,
C. ,, D. ,,
8.如图所示,两个相同材料制成的靠摩擦转动的轮和轮水平放置两轮不打滑,两轮半径。当主动轮匀速转动时,在轮边缘上放置的小木块恰能相对静止。若将小木块放在轮上,欲使小木块相对轮静止,则木块距轮转轴的最大距离为 ( )
A. B. C. D.
9.如图所示,支架固定在底座上,它们的总质量为。质量分别为和的小球、可视为质点固定在一根长度为的轻杆两端,该轻杆通过光滑转轴安装在支架的横梁上,、间的距离为,两小球和轻杆一起绕轴在竖直平面内做圆周运动,运动过程中支架和底座一直保持静止。当转动到图示竖直位置时,小球的速度为,重力加速度为。对于该位置,下列说法正确的是( )
A. 小球、的向心加速度大小相等
B. 小球的向心力大于球的向心力
C. 若,则底座对水平地面的压力为
D. A、两球恰好做匀速圆周运动
10.如图所示,竖直平面内有一“”型光滑细杆,杆与水平面间夹角均为,杆上套有形状相同质量不同的小球、,现让杆绕底部点所在的竖直轴匀速转动,下列说法不正确的是( )
A. 两球的角速度大小相同
B. 两球的向心加速度大小不同
C. 两球始终处于同一高度
D. 若杆瞬间停止转动,则停转后两球的加速度大小相等
11.如图为某游乐园飓风飞椅结构简图其装置由伞型转盘、中间圆柱、底座和软绳悬挂飞椅可视为质点组成,在距转盘下表面轴心距离为的圆周上,用软绳分布均匀地悬挂座飞椅,飞椅与人的质量之和均为,悬挂飞椅的绳长均为,当水平转盘以角速度稳定旋转时,各软绳与竖直方向成角。则下列判断正确的是( )
A. 转盘旋转线速度为
B. 软绳的拉力大小为
C. 软绳与竖直方向夹角大小与软绳长短无关
D. 软绳与竖直方向夹角大小与乘客质量大小无关
二、多选题
12.如图所示,水平圆盘绕过其圆心的竖直轴匀速转动,圆盘上距离圆心为的位置有一个质量的小物体小物体可视为质点,小物体与圆盘间的动摩擦因数,小物体始终与圆盘保持相对静止,最大静摩擦力等于滑动摩擦力,取。下列说法中正确的是( )
A. 若,圆盘的最大角速度为
B. 若,圆盘的最大转速为
C. 若圆盘角速度大小为,则一定不大于
D. 若圆盘角速度大小为,则小物块的线速度不大于
13.如图所示,、是“旋转秋千”中的两个座椅,通过相同长度的缆绳悬挂在旋转圆盘上,不考虑空气阻力的影响,当旋转圆盘绕竖直的中心轴匀速转动时,悬挂、的绳与竖直方向的夹角不相等,则下列说法正确的是( )
A. 的速度比的速度大 B. 与的向心加速度大小相等
C. 的转动半径小于的转动半径 D. 与的转动周期相等
14.如图所示,长为的悬线固定在点,在点正下方有一钉子,长为,把悬线另一端的小球拉到跟悬点在同一水平面上无初速度地释放,小球运动到悬点正下方时悬线碰到钉子的瞬间 ( )
A. 小球的线速度突然增大为原来的倍
B. 小球的角速度突然增大为原来的倍
C. 小球的向心力突然增大为原来的倍
D. 小球的所受悬线的拉力突然增大为原来的倍
15.某学校的机动车出入口采用如图所示的曲杆道闸,道闸由转动杆与横杆链接而成,、为横杆的两个端点。某天中午快递员将快递袋子挂在了校门口道闸的横杆上,由于门卫没有及时将快递袋取下,在道闸抬起过程中,快递袋始终与横杆保持相对静止,且杆始终水平,此过程中杆绕点从水平方向匀速转动到接近竖直方向。若快递袋可视为质点,与横杆之间的动摩擦因数为,最大静摩擦力等于滑动摩擦力,转动杆长度为,重力加速度为。下列说法正确的是( )
A. 、两点的加速度不同
B. 点的加速度始终沿方向
C. 、两点都在做匀速圆周运动
D. 快递袋能够与横杆保持相对静止一起运动的最大速率
三、实验题
16.如图所示,某兴趣小组利用电动机驱动轻杆带动小球做竖直面内的匀速圆周运动,改变小球质量,通过力传感器获得轻杆拉力最大值随小球质量变化的关系,并求得当地的重力加速度。
为了测得当地的重力加速度,至少还应该知道________填选项序号。
A.小球做圆周运动的周期 小球做圆周运动的半径 力传感器的质量
采用图像法处理数据时,应该作出________填“”或者“”图像,若图像斜率为,当地的重力加速度________用和中已知量表示。
17.某兴趣小组的同学设计了图所示的装置,用来测量滑块质量滑块可视为质点和滑块与水平台面间的动摩擦因数。水平转台能绕竖直的轴匀速转动,装有遮光条的小滑块放置在转台上,不可伸长的细线一端连接小滑块,另一端连到固定在转轴上的力传感器上,连接到计算机上的传感器能显示细线的拉力,安装在铁架台上的光电门可以读出遮光条通过光电门的挡光时间,兴趣小组采取了下列步骤:
用游标卡尺测量遮光条的宽度;
将滑块放置在转台上,使细线刚好绷直,量出滑块到转轴的距离;
控制转台以某一角速度匀速转动,记录力传感器和光电门的示数,分别为和;依次增大转台的角速度,并保证其每次都做匀速转动,记录对应的力传感器示数、和光电门的示数、。回答下面的问题:
滑块匀速转动的线速度可表示为______用、中字母表示。
如图,当大于时,滑块做匀速圆周运动的向心力由哪些力提供( )
A.绳子的拉力 转盘的摩擦力 绳子的拉力和转盘的摩擦力
处理数据时,兴趣小组的同学以力传感器的示数为纵轴,为横轴,建立直角坐标系,描点后拟合为一条直线,如图所示图中、已知,设最大静摩擦力等于滑动摩擦力,重力加速度为,则物块的质量______,动摩擦因数______。用、、、中字母表示
四、计算题
18.如图所示,半径为的半球形陶罐,固定在可以绕竖直轴旋转的水平转台上,转台转轴与过陶罐球心的对称轴重合,转台以一定角速度匀速旋转.一质量为的小物块落入陶罐内,经过一段时间后,小物块随陶罐一起转动且相对罐壁静止,它和点的连线与之间的夹角为重力加速度大小为.
求出物块线速度大小;
若时,小物块受到的摩擦力恰好为零,求;
若为第问的值,且,求小物块受到的摩擦力大小;
19.一种离心测速器的简化工作原理如图所示。细杆的一端固定在竖直转轴上的点,并可随轴一起转动。杆上套有一轻质弹簧,弹簧一端固定于点,另一端与套在杆上的圆环相连。当测速器稳定工作时,圆环将相对细杆静止,通过圆环的位置可以确定细杆匀速转动的角速度。已知细杆长度,杆与竖直转轴的夹角始终为,弹簧原长,弹簧劲度系数,圆环质量;弹簧始终在弹性限度内,摩擦力可忽略不计
若细杆和圆环处于静止状态,求圆环到点的距离;
求弹簧处于原长时,细杆匀速转动的角速度大小;
求圆环处于细杆末端时,细杆匀速转动的角速度大小。
20.如图所示,半径为的水平圆盘距地面的高度,质量均的、两个物块,均可看成质点,用一根不可伸长的轻绳连在一起,轻绳经过圆盘圆心,、两物块的转动半径,在转盘边缘。和一起随圆盘绕竖直中心轴转动为转盘圆心在地面沿竖直方向的投影,转动角速度从零开始缓慢增大,直到有物块相对圆盘运动为止。它们与圆盘间的动摩擦因数均为。取最大静摩擦力等于滑动摩擦力,不计空气阻力,重力加速度为,求:
当绳上恰好出现拉力时,圆盘的角速度大小;
绳上出现拉力后,随着角速度的缓慢增加,是否有物体受到的摩擦力为零?如果有,求出此时圆盘角速度大小;
若水平圆盘距地面的高度为,随着角速度进一步缓慢增加,两物块相对圆盘滑动,假设滑动瞬间绳子断裂,求落地的位置与之间的距离。
答案和解析
1.
【解析】由,可知AB错误;
C.运动至圆心等高处时,所受摩天轮的作用力,故C正确;
D.由座舱做匀速圆周运动,可知座舱所受的合力提供向心力,,方向始终指向摩天轮中心,则座舱在最低点时,其所受摩天轮的作用力为,最高点时,其所受摩天轮的作用力为,故D错误。
2.
【解析】半径为的大齿轮匀速率转动,大齿轮与半径为的中齿轮垂直咬合,二者线速度相等,,中齿轮通过横轴与半径为小齿轮相连,二者角速度相等,抽水桶的运动速率,故A项正确。
3.
【解析】A. 鼓形轮的角速度为,故A错误;
B. 小球所需的向心力大小为
若,则杆对小球的作用力竖直向下,故B错误;
C. 对小球,竖直方向有
水平方向有
则杆对小球的作用力为,故C错误;
D. 对小球,根据牛顿第二定律可得
可知杆对小球的作用力一定大于,故D正确。
故选D。
4.
【解析】A、根据角速度和周期的关系可知,周期,故A错误;
B、根据线速度与角速度的关系可得,线速度大小,故B错误;
C、座舱做匀速圆周运动,其向心力由重力和摩天轮对座舱的作用力的合力提供,根据牛顿第二定律,这里是合力并非摩天轮对座舱的作用力,故 C错误;
D、当座舱运动至与圆心等高位置时,向心力由摩天轮对座舱的作用力的水平分力提供,竖直方向上摩天轮对座舱的作用力的竖直分力与重力平衡,即。根据力的合成,此时摩天轮对座舱的作用力,显然,所以选项正确。
5.
【解析】A.由 , ,可得,故A错误;
B.、两点为同轴转动,角速度相等,,由得周期相等,,可得,故B错误;
C.由,得,故C正确;
D.由,可得,故D错误。
6.
【解析】对其中一个小球受力分析,如图
受重力,绳子的拉力,由于小球做匀速圆周运动,故重力和拉力合力提供向心力,由几何关系和向心力公式得
设绳子与悬挂点间的高度差为,由几何关系,得
联立得
则角速度与绳子的长度和转动半径无关,根据 可得周期相同,A正确、C错误;
B.由 ,可知线速度与做圆周运动半径成正比,但两球做圆周运动半径不同,则线速度大小不相同,B错误;
D.两球的角速度相同,但两球做圆周运动半径不等,由 得,两球向心加速度不等,D错误。
故选A。
7.
【解析】设圆周运动所在平面与的高度为,圆周半径为,则,
,解上式得:,所以线速度与角度、半径无关,因此。
由于圆周半径为根据,,可知,,故B正确ACD错误。
8.
【解析】和用相同材料制成的靠摩擦传动,边缘线速度相同,则
而。
所以
对于在边缘的木块,最大静摩擦力恰为向心力,即
当在轮上恰要滑动时,设此时半径为
则
解得
故ABD错误,C正确。
故选C。
9.
【解析】A.两小球和轻杆一起绕轴在竖直平面内做圆周运动,所以两小球的角速度相同,根据可知小球、的加速度之比为::,故A错误;
B.根据可知、的向心力之比为::,故B错误;
C.若,对分析则有,解得轻杆对支持力为,根据可知,对分析则有,解得轻杆对拉力为,以底座和轻杆为对象,水平地面对底座的支持力为,所以底座对水平地面的压力为,故C错误;
D. 由分析知向心力之比为::,故两球恰好做匀速圆周运动,故D正确;
10.
【解析】A.让杆绕底部点所在的竖直轴匀速转动,两个小球同轴转动,角速度相等,故A正确,不合题意;
分析小球受力可知:,,则,所以两球圆周运动的半径相等,始终处于同一高度;
向心加速度:,相等,故B错误,符合题意,C正确,不合题意;
D.若杆瞬间停止转动,停转后,分析小球受力可知:,,则小球加速度,所以两球的加速度大小相等,故D正确,不合题意。
故选B。
11.
【解析】A.如图所示,对质点受力分析,由牛顿第二定律可得:,根据几何关系可得:,解得转盘旋转角速度为,故A错误;
B.绳中的拉力,故B错误;
根据:,软绳与竖直方向夹角大小只与转速和软绳长短有关,与乘客质量无关,故D正确,C错误。
故选D。
12.
【解析】小物体始终与圆盘保持相对静止,所以静摩擦力提供向心力,即。
当摩擦力等于最大静摩擦力时,角速度达到最大、转速达到最大。
即,若,,转速,故A正确、B错误;
由的分析可知,。若圆盘角速度大小为,则
由可知,,故C正确、D错误。
13.
【解析】解:设坐椅的悬挂点到转轴的距离为,绳长为。对座椅受力分析如图:
C、两个座椅具有相同的角速度,由牛顿第二定律可知,结合题意可得,的转动半径小于的转动半径,故C正确;
A、两个座椅具有相同的角速度,根据公式,的转动半径小于的半径,则的线速度小于的线速度,故A错误;
B、根据公式,的转动半径小于的半径,两个座椅具有相同的角速度,则的向心加速度小于的向心加速度,故B错误;
D、根据公式,两个座椅具有相同的角速度,故A与的转动周期相等,故D正确。
故选:。
14.
【解析】A.悬线与钉子碰撞前后,线的拉力始终与小球运动方向垂直,小球的线速度不变。故A错误;
B.当半径减小时,由变大为原来的倍,故B正确;
C.由知向心力突然增大为原来的倍,故C正确;
D.而在最低点,故碰到钉子后合力变为原来的倍,悬线拉力变大,但不是原来的倍,故D错误。
故选BC。
15.
【解析】、、两点相对静止,运动状态相同,加速度相同,均做匀速圆周运动,A错误,C正确;
B、由前分析知,点加速度始终和方向平行即和点加速度同向,B错误;
D、设快递袋质量为,做圆周运动时向心加速度和水平方向夹角为,如图:
由,,,
联立得,其中,由数学知识可知,最大值为,D正确。
16.;;。
【解析】最低点时拉力最大,满足,解得,
所以还需要知道小球做匀速圆周运动的周期和半径,
故选AB。
作图像,且图像的斜率,解得。
17.;;;
【解析】滑块匀速转动的线速度 ;
当 小于时,静摩擦力提供向心力,此时拉力为零,当 大于 时,静摩擦力不足以提供向心力,还需要有绳子的拉力,故选C。
对在转台上做匀速圆周运动的滑块,当 大于 时,
由牛顿第二定律有 ,
解得: ,
根据图乙可知
,解得: ,
,解得:.
18.解:转动的线速度:
小物块在水平面内做匀速圆周运动,当小物块受到的摩擦力恰好等于零时,小物块所受的重力和陶罐的支持力的合力提供圆周运动的向心力,
有:
解得:
当时,小物块受到的摩擦力沿陶罐壁切线向下,设摩擦力的大小为,陶罐壁对小物块的支持力为,沿水平和竖直方向建立坐标系,则:
水平方向:
竖直方向:
代入数据解得:
同理,当时,小物块受到的摩擦力沿陶罐壁切线向上,则:
水平方向:
竖直方向:
代入数据解得:。
19.解:静止时对圆环受力分析有:
解得: ;
对圆环有:水平方向:
竖直方向:
解得: ;
圆环处于细杆末端时,对圆环受力分析,受重力,弹簧伸长,弹力沿杆向下。
根据胡克定律得,
根据对圆环受力分析,并正交分解,竖直方向受力平衡,水平方向合力提供向心力,
则有,
由几何关系得,
联立解得。
20.解:绳上恰好出现拉力时,与转盘之间为最大静摩擦力,即最大静摩擦力提供其向心力,则有:
解得圆盘的角速度为: ,即当绳上恰好出现拉力时,圆盘的角速度大小为;
绳上出现拉力后,随着角速度的缓慢增加,此时对物体受力分析有: ,对物体受力分析有: ,联立两式可得:
,可知:随着角速度的缓慢增加,物体收到的摩擦力逐渐减小,当 时,即: ,可得: ;
当圆盘的角速度大于时,此时对物体受力分析有: ,对物体受力分析有:,联立两式可得: ,可知:随着角速度的缓慢增加,物体收到的摩擦力逐渐增大,当物体受到的静摩擦力最大时,两物块即将相对圆盘滑动,即: ,可得: ,此时物体是速度 ,此后物体将做平抛运动,有: , ,联立两式带入数据可得:,由几何关系可知: 落地的位置与之间的距离.
第11页,共17页
