2025年中考数学二轮复习-专题14二次函数与面积【课件】(共29张PPT)
文档属性
| 名称 | 2025年中考数学二轮复习-专题14二次函数与面积【课件】(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 999.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 19:38:45 | ||
图片预览



文档简介
(共29张PPT)
专题十四 二次函数与面积
第二篇 专题拓展·提能力
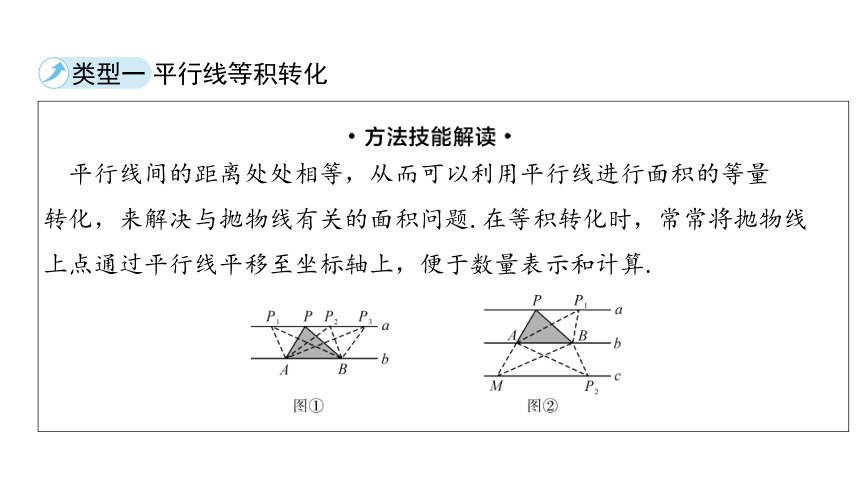
类型一 平行线等积转化
平行线间的距离处处相等,从而可以利用平行线进行面积的等量
转化,来解决与抛物线有关的面积问题.在等积转化时,常常将抛物线
上点通过平行线平移至坐标轴上,便于数量表示和计算.
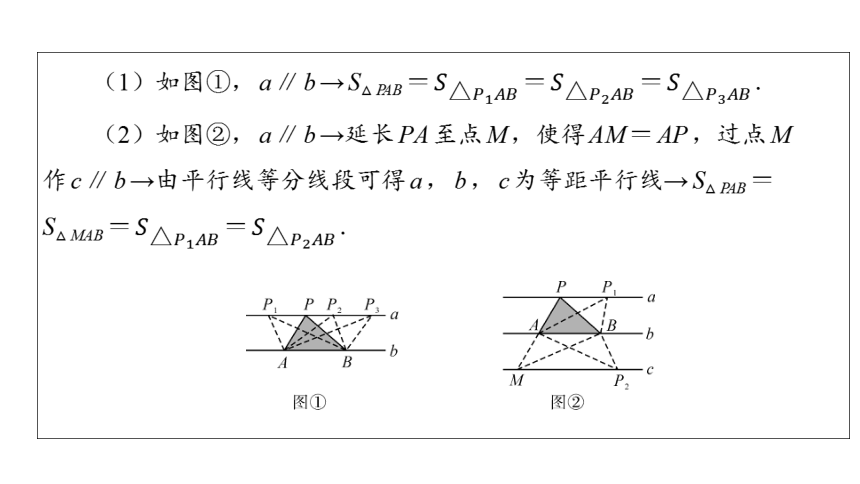
(1)如图①,a∥b→S△PAB= = = .
(2)如图②,a∥b→延长PA至点M,使得AM=AP,过点M
作c∥b→由平行线等分线段可得a,b,c为等距平行线→S△PAB=
S△MAB= = .
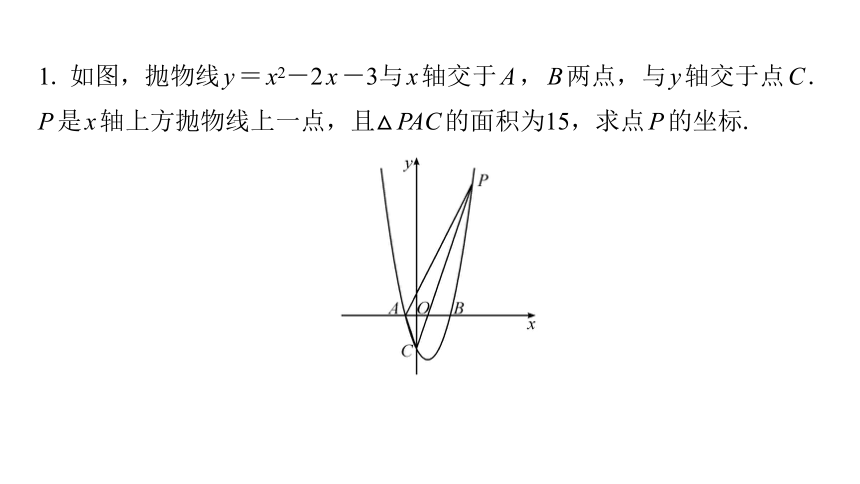
1. 如图,抛物线y=x2-2x-3与x轴交于A,B两点,与y轴交于点C.
P是x轴上方抛物线上一点,且△PAC的面积为15,求点P的坐标.
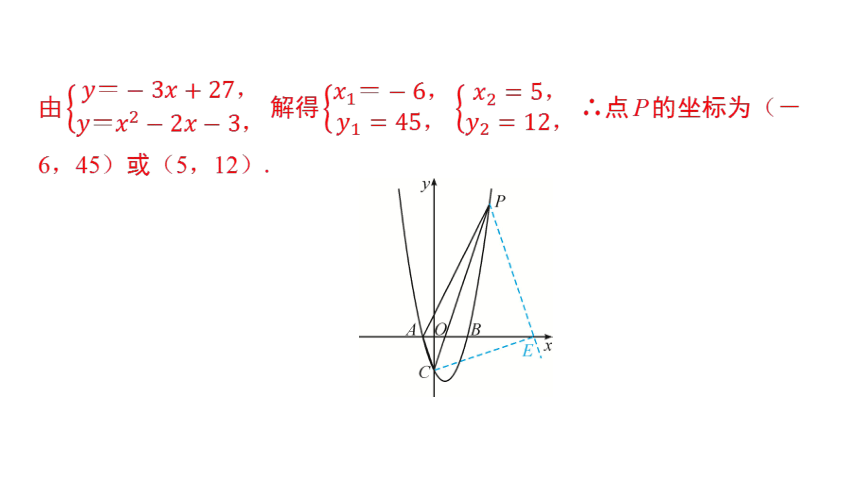
解:如图,过点P作PE∥AC,交x轴于点E,连接CE,则S△EAC=S△PAC=15.
易得A(-1,0),B(3,0),C(0,-3),
∴S△EAC= AE·OC= ×AE×3=15,∴AE=10,
∴OE=AE-OA=9,∴点E的坐标为(9,0),易得直线AC的解析式为y=-3x-3.
设直线PE的解析式为y=-3x+b.将E(9,0)代入可得b=27,∴y=-3x+27.
由 解得 ∴点P的坐标为(-
6,45)或(5,12).
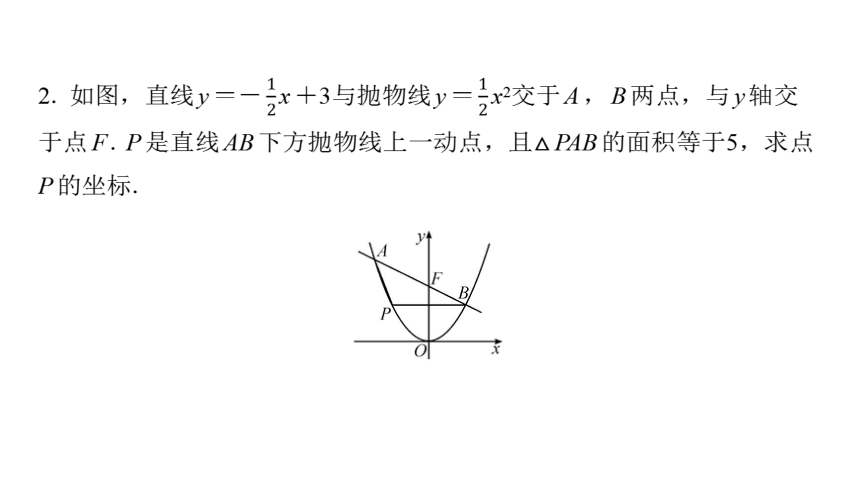
2. 如图,直线y=- x+3与抛物线y= x2交于A,B两点,与y轴交
于点F. P是直线AB下方抛物线上一动点,且△PAB的面积等于5,求点
P的坐标.
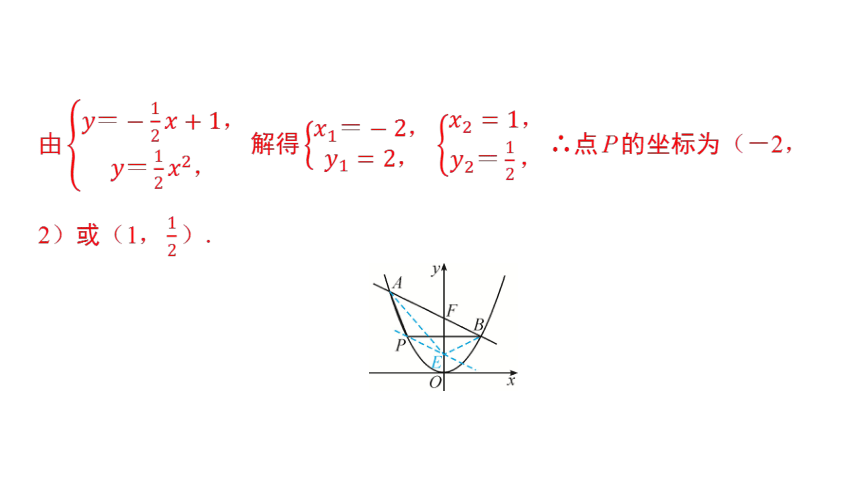
解:如图,过点P作PE∥AB,交y轴于点E,连接AE,BE,则S△EAB=S△PAB=5.
易得A(-3, ),B(2,2),F(0,3),
∴S△EAB= EF·|xB-xA|= ×EF×(2+3)=5,
∴EF=2,OE=OF-EF=1,∴点E的坐标为(0,1),∴直线PE的解析式为y=- x+1.
由 解得 ∴点P的坐标为(-2,
2)或(1, ).
类型二 二次函数中三角形的面积最值
在解决抛物线上动态三角形面积最值问题时,一般思路:设动点
坐标→建立动态三角形面积与动点坐标参量的函数解析式→利用函数
的增减性确定面积的最值.
建立动态三角形面积与动点坐标参量函数解析式常有如下方法:
1. 如图,抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点
C,点B的坐标为(1,0),对称轴是直线x=-1.
(1)求抛物线的解析式;
解:(1)抛物线的解析式为y=x2+2x-3.
(2)P是直线AC下方抛物线上一个动点,连接PA,PC,BC,求四
边形PABC面积的最大值,并求出此时点P的坐标.
解:(2)如图,过点P作PM⊥x轴于点M,交直线AC
于点N. 易得A(-3,0),B(1,0),C(0,-3),
∴S△ABC= ×4×3=6.易得直线AC的解析式为y=-x-3.
设P(m,m2+2m-3),-3<m<0,则N(m,-m-3),
∴PN=-m-3-(m2+2m-3)=-m2-3m,
∴S△PAC= PN· = ×(-m2-3m)×3=- m2- m,
∴S四边形PABC=S△PAC+S△ABC=- m2- m+6=- + ,
∴当m=- 时,四边形PABC的面积最大,最大值为 ,此时点P坐标为(- ,- ).
2. [2024·成都节选]如图,在平面直角坐标系中,抛物线
y=ax2-2ax-3a(a>0)与x轴交于A,B两点(点A在点B的左侧),其顶点为C,D是抛物线第四象限上一点.
(1)求线段AB的长;
解:(1)由ax2-2ax-3a=0,解得x1=3,x2=-1,
∴A(-1,0),B(3,0),∴AB=4.
(2)当a=1时,若△ACD的面积与△ABD的面积相等,求tan∠ABD
的值.
解:(2)当a=1时,y=x2-2x-3=(x-1)2-4,
∴顶点C(1,-4),
设D(m,m2-2m-3),其中0<m<3.
如图,连接AC,CD,DB,AD,过点D作DM⊥x轴于点M,作对称轴交AD于点N,
∴S△ABD= ×4×(-m2+2m+3)=-2m2+4m+6.设直线AD的解析式为y=kx+b,将A(-1,0),D(m,m2-2m-3)代入,
得 解得
∴y=(m-3)x+m-3.
当x=1时,y=2m-6,∴N(1,2m-6),∴CN=2m-6-
(-4)=2m-2,
∴S△ACD= CN·|xD-xA|= ×(2m-2)×(m+1)=m2-1.
∵S△ABD=S△ACD,∴-2m2+4m+6=m2-1,解得m1= ,m2=-1
(舍去),
∴D( ,- ),∴DM= ,BM=3- = ,
∴tan∠ABD=tan∠DBM= = = .
3. 如图,在平面直角坐标系中,已知抛物线y=ax2+bx经过A(4,
0),B(1,4)两点.P是抛物线上一点,且在直线AB的上方.
(1)求抛物线的解析式.
解:(1)抛物线的解析式为y=- x2+ x.
(2)如图①,若△OAB面积是△PAB面积的2倍,求点P的坐标.
解:(2)如图①,过点P作PM∥y轴,交AB于点M.
易得直线AB的解析式为y=- x+ .
设P(m,- m2+ m),1<m<4,则M(m,- m+ ),
∴PM=- m2+ m-(- m+ )=- m2+ m- ,
∴S△PAB= PM· = ×(- m2+ m- )×3=
-2m2+10m-8.
∵S△OAB= ×4×4=8,2S△PAB=S△OAB,∴2×(-2m2+10m-8)=8,解得m1=2,m2=3,
∴点P的坐标为(2, )或(3,4).
(3)如图②,OP交AB于点C,PD∥BO交AB于点D. 记△CDP,
△CPB,△CBO的面积分别为S1,S2,S3,判断 + 是否存在最大
值.若存在,求出最大值;若不存在,请说明理由.
(3)如图②,过点P作PH⊥x轴于点H,交AB于点
G,延长AB交y轴于点F,则F(0, ).
∵PD∥BO,∴ = = ,∴ + = + = .
∵PD∥BO,∴∠PDC=∠OBC,∴∠PDG=∠OBF. ∵PG∥OF,
∴∠PGD=∠OFB,
∴△PDG∽△OBF,∴ = ,∴ + = = = PG.
设P(n,- n2+ n),1<n<4,则G(n,- n+ ),∴PG
=- n2+ n- ,
∴ + = PG= ×(- n2+ n- )=- + .
又∵1<n<4,∴当n= 时, + 存在最大值,最大值为 .
谢谢观看
专题十四 二次函数与面积
第二篇 专题拓展·提能力
类型一 平行线等积转化
平行线间的距离处处相等,从而可以利用平行线进行面积的等量
转化,来解决与抛物线有关的面积问题.在等积转化时,常常将抛物线
上点通过平行线平移至坐标轴上,便于数量表示和计算.
(1)如图①,a∥b→S△PAB= = = .
(2)如图②,a∥b→延长PA至点M,使得AM=AP,过点M
作c∥b→由平行线等分线段可得a,b,c为等距平行线→S△PAB=
S△MAB= = .
1. 如图,抛物线y=x2-2x-3与x轴交于A,B两点,与y轴交于点C.
P是x轴上方抛物线上一点,且△PAC的面积为15,求点P的坐标.
解:如图,过点P作PE∥AC,交x轴于点E,连接CE,则S△EAC=S△PAC=15.
易得A(-1,0),B(3,0),C(0,-3),
∴S△EAC= AE·OC= ×AE×3=15,∴AE=10,
∴OE=AE-OA=9,∴点E的坐标为(9,0),易得直线AC的解析式为y=-3x-3.
设直线PE的解析式为y=-3x+b.将E(9,0)代入可得b=27,∴y=-3x+27.
由 解得 ∴点P的坐标为(-
6,45)或(5,12).
2. 如图,直线y=- x+3与抛物线y= x2交于A,B两点,与y轴交
于点F. P是直线AB下方抛物线上一动点,且△PAB的面积等于5,求点
P的坐标.
解:如图,过点P作PE∥AB,交y轴于点E,连接AE,BE,则S△EAB=S△PAB=5.
易得A(-3, ),B(2,2),F(0,3),
∴S△EAB= EF·|xB-xA|= ×EF×(2+3)=5,
∴EF=2,OE=OF-EF=1,∴点E的坐标为(0,1),∴直线PE的解析式为y=- x+1.
由 解得 ∴点P的坐标为(-2,
2)或(1, ).
类型二 二次函数中三角形的面积最值
在解决抛物线上动态三角形面积最值问题时,一般思路:设动点
坐标→建立动态三角形面积与动点坐标参量的函数解析式→利用函数
的增减性确定面积的最值.
建立动态三角形面积与动点坐标参量函数解析式常有如下方法:
1. 如图,抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点
C,点B的坐标为(1,0),对称轴是直线x=-1.
(1)求抛物线的解析式;
解:(1)抛物线的解析式为y=x2+2x-3.
(2)P是直线AC下方抛物线上一个动点,连接PA,PC,BC,求四
边形PABC面积的最大值,并求出此时点P的坐标.
解:(2)如图,过点P作PM⊥x轴于点M,交直线AC
于点N. 易得A(-3,0),B(1,0),C(0,-3),
∴S△ABC= ×4×3=6.易得直线AC的解析式为y=-x-3.
设P(m,m2+2m-3),-3<m<0,则N(m,-m-3),
∴PN=-m-3-(m2+2m-3)=-m2-3m,
∴S△PAC= PN· = ×(-m2-3m)×3=- m2- m,
∴S四边形PABC=S△PAC+S△ABC=- m2- m+6=- + ,
∴当m=- 时,四边形PABC的面积最大,最大值为 ,此时点P坐标为(- ,- ).
2. [2024·成都节选]如图,在平面直角坐标系中,抛物线
y=ax2-2ax-3a(a>0)与x轴交于A,B两点(点A在点B的左侧),其顶点为C,D是抛物线第四象限上一点.
(1)求线段AB的长;
解:(1)由ax2-2ax-3a=0,解得x1=3,x2=-1,
∴A(-1,0),B(3,0),∴AB=4.
(2)当a=1时,若△ACD的面积与△ABD的面积相等,求tan∠ABD
的值.
解:(2)当a=1时,y=x2-2x-3=(x-1)2-4,
∴顶点C(1,-4),
设D(m,m2-2m-3),其中0<m<3.
如图,连接AC,CD,DB,AD,过点D作DM⊥x轴于点M,作对称轴交AD于点N,
∴S△ABD= ×4×(-m2+2m+3)=-2m2+4m+6.设直线AD的解析式为y=kx+b,将A(-1,0),D(m,m2-2m-3)代入,
得 解得
∴y=(m-3)x+m-3.
当x=1时,y=2m-6,∴N(1,2m-6),∴CN=2m-6-
(-4)=2m-2,
∴S△ACD= CN·|xD-xA|= ×(2m-2)×(m+1)=m2-1.
∵S△ABD=S△ACD,∴-2m2+4m+6=m2-1,解得m1= ,m2=-1
(舍去),
∴D( ,- ),∴DM= ,BM=3- = ,
∴tan∠ABD=tan∠DBM= = = .
3. 如图,在平面直角坐标系中,已知抛物线y=ax2+bx经过A(4,
0),B(1,4)两点.P是抛物线上一点,且在直线AB的上方.
(1)求抛物线的解析式.
解:(1)抛物线的解析式为y=- x2+ x.
(2)如图①,若△OAB面积是△PAB面积的2倍,求点P的坐标.
解:(2)如图①,过点P作PM∥y轴,交AB于点M.
易得直线AB的解析式为y=- x+ .
设P(m,- m2+ m),1<m<4,则M(m,- m+ ),
∴PM=- m2+ m-(- m+ )=- m2+ m- ,
∴S△PAB= PM· = ×(- m2+ m- )×3=
-2m2+10m-8.
∵S△OAB= ×4×4=8,2S△PAB=S△OAB,∴2×(-2m2+10m-8)=8,解得m1=2,m2=3,
∴点P的坐标为(2, )或(3,4).
(3)如图②,OP交AB于点C,PD∥BO交AB于点D. 记△CDP,
△CPB,△CBO的面积分别为S1,S2,S3,判断 + 是否存在最大
值.若存在,求出最大值;若不存在,请说明理由.
(3)如图②,过点P作PH⊥x轴于点H,交AB于点
G,延长AB交y轴于点F,则F(0, ).
∵PD∥BO,∴ = = ,∴ + = + = .
∵PD∥BO,∴∠PDC=∠OBC,∴∠PDG=∠OBF. ∵PG∥OF,
∴∠PGD=∠OFB,
∴△PDG∽△OBF,∴ = ,∴ + = = = PG.
设P(n,- n2+ n),1<n<4,则G(n,- n+ ),∴PG
=- n2+ n- ,
∴ + = PG= ×(- n2+ n- )=- + .
又∵1<n<4,∴当n= 时, + 存在最大值,最大值为 .
谢谢观看
同课章节目录
