2.1.2求曲线方程
图片预览




文档简介
课件11张PPT。2.1.2 求曲线的方程 上一节,我们已经建立了曲线的方程.方程的曲线的概念.利用这两个重要概念,就可以借助于坐标系,用坐标表示点,把曲线看成满足某种条件的点的集合或轨迹,用曲线上点的坐标(x, y)所满足的方程f (x, y)=0表示曲线,通过研究方程的性质间接地来研究曲线的性质.这一节,我们就来学习这一方法.复习回顾:1.解析几何与坐标法:
我们把借助于坐标系研究几何图形的方法叫做坐标法. 在数学中,用坐标法研究几何图形的知识形成了一门叫解析几何的学科.因此,解析几何是用代数方法研究几何问题的一门数学学科.2.平面解析几何研究的主要问题:
(1)根据已知条件,求出表示平面曲线的方程;(2)通过方程,研究平面曲线的性质.
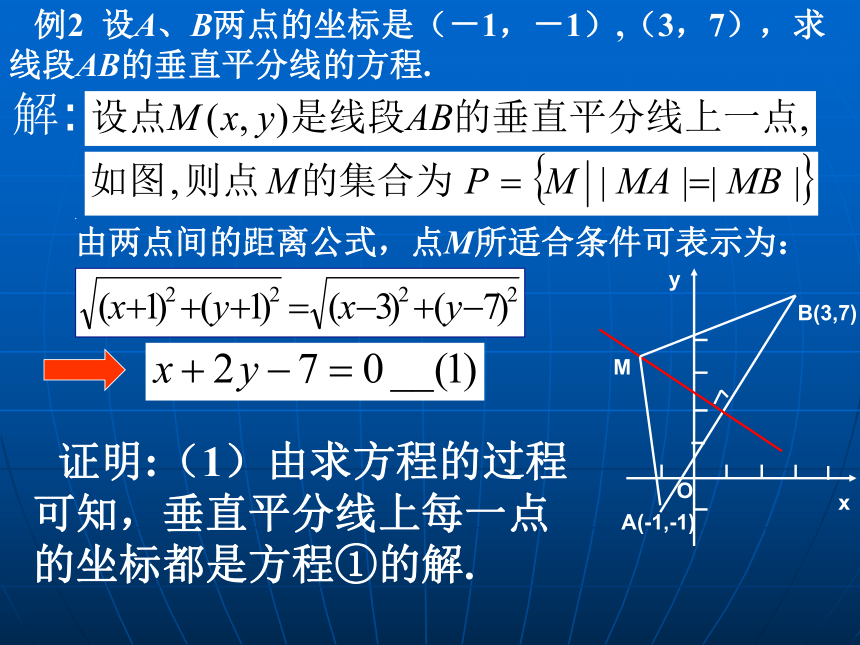
说明:本节主要讨论求解曲线方程的一般步骤.例2 设A、B两点的坐标是(-1,-1),(3,7),求线段AB的垂直平分线的方程..
由两点间的距离公式,点M所适合条件可表示为:证明:(1)由求方程的过程可知,垂直平分线上每一点的坐标都是方程①的解.
解:即点M1在线段AB的垂直
平分线上.
由(1)、(2)可知方程
①是线段AB的垂直平分线
的方程.由上面的例子可以看出,求曲线(图形)的方程,一般有下面几个步骤:
(1)建立适当的坐标系,用有序实数对(x, y)表示曲线上任意一点M的坐标;
(2)写出适合条件P的点M的集合P ={M | P(M)};
(3)用坐标表示条件P(M),列出方程f(x,y)=0;
(4)化方程f(x,y)=0为最简形式;
(5)证明以化简后的方程的解为坐标的点都是曲线上的点.说明:一般情况下,化简前后方程的解集是相同的,步骤(5)可以省略不写,如有特殊情况,可适当予以说明.另外,根据情况,也可以省略步骤(2),直接列出曲线方程.例3 已知一条曲线在x轴的上方,它上面的每一点到点(0,2)的距离减去它到x轴的距离的差都是2,求这条曲 线的方程.因为曲线在x轴的上方,所以y>0,虽然原点O的坐(0,0)是这个方程的解,但不属于已知曲线,所以曲线的方程是 它的图形是关于y轴对称的抛物线,但不包括抛物线的顶点.解: 通过上述两个例题了解坐标法的解题方法,明确建立适当的坐标系是求解曲线方程的基础;同时,根据曲线上的点所要适合的条件列出等式,是求曲线方程的重要环节,在这里常用到一些基本公式,如两点间距离公式,点到直线的距离公式,直线的斜率公式等,因此先要了解上述知识,必要时作适当复习.
●课堂小结
通过本节学习,要求大家初步认识坐标法研究几何问题的知识与观点,进而逐步掌握求曲线的方程的一般步骤.1、求到坐标原点的距离等于 2 的轨迹方程. x 2 + y 2 = 42、已知点 M 与 x 轴的距离和它与点 F ( 0 , 4 )
的距离相等,求点 M 的轨迹方程. x 2 -8y + 16 = 03、求证:到点 P ( 0 , 1 ) 和直线 :y = -1
距离相等的点的轨迹方程是 y = x 2 练习 小结 同学们,这节课我们有什么收获呢?课本:P37 习题A 2, 3
P37 习题B 1, 2课后作业
我们把借助于坐标系研究几何图形的方法叫做坐标法. 在数学中,用坐标法研究几何图形的知识形成了一门叫解析几何的学科.因此,解析几何是用代数方法研究几何问题的一门数学学科.2.平面解析几何研究的主要问题:
(1)根据已知条件,求出表示平面曲线的方程;(2)通过方程,研究平面曲线的性质.
说明:本节主要讨论求解曲线方程的一般步骤.例2 设A、B两点的坐标是(-1,-1),(3,7),求线段AB的垂直平分线的方程..
由两点间的距离公式,点M所适合条件可表示为:证明:(1)由求方程的过程可知,垂直平分线上每一点的坐标都是方程①的解.
解:即点M1在线段AB的垂直
平分线上.
由(1)、(2)可知方程
①是线段AB的垂直平分线
的方程.由上面的例子可以看出,求曲线(图形)的方程,一般有下面几个步骤:
(1)建立适当的坐标系,用有序实数对(x, y)表示曲线上任意一点M的坐标;
(2)写出适合条件P的点M的集合P ={M | P(M)};
(3)用坐标表示条件P(M),列出方程f(x,y)=0;
(4)化方程f(x,y)=0为最简形式;
(5)证明以化简后的方程的解为坐标的点都是曲线上的点.说明:一般情况下,化简前后方程的解集是相同的,步骤(5)可以省略不写,如有特殊情况,可适当予以说明.另外,根据情况,也可以省略步骤(2),直接列出曲线方程.例3 已知一条曲线在x轴的上方,它上面的每一点到点(0,2)的距离减去它到x轴的距离的差都是2,求这条曲 线的方程.因为曲线在x轴的上方,所以y>0,虽然原点O的坐(0,0)是这个方程的解,但不属于已知曲线,所以曲线的方程是 它的图形是关于y轴对称的抛物线,但不包括抛物线的顶点.解: 通过上述两个例题了解坐标法的解题方法,明确建立适当的坐标系是求解曲线方程的基础;同时,根据曲线上的点所要适合的条件列出等式,是求曲线方程的重要环节,在这里常用到一些基本公式,如两点间距离公式,点到直线的距离公式,直线的斜率公式等,因此先要了解上述知识,必要时作适当复习.
●课堂小结
通过本节学习,要求大家初步认识坐标法研究几何问题的知识与观点,进而逐步掌握求曲线的方程的一般步骤.1、求到坐标原点的距离等于 2 的轨迹方程. x 2 + y 2 = 42、已知点 M 与 x 轴的距离和它与点 F ( 0 , 4 )
的距离相等,求点 M 的轨迹方程. x 2 -8y + 16 = 03、求证:到点 P ( 0 , 1 ) 和直线 :y = -1
距离相等的点的轨迹方程是 y = x 2 练习 小结 同学们,这节课我们有什么收获呢?课本:P37 习题A 2, 3
P37 习题B 1, 2课后作业
