第二十二章二次函数培优练习卷(含答案) 人教版九年级数学上册
文档属性
| 名称 | 第二十二章二次函数培优练习卷(含答案) 人教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 550.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 19:13:19 | ||
图片预览




文档简介
第二十二章 二次函数 培优练习卷
选择题(每小题4分,共40分)
1、已知函数,其图象是抛物线, 则的取值是
A . B . C . D .
2、已知抛物线过,,,四点,则与的大小关系是
A. B. C. D.不能确定
3、如图,一次函数与二次函数图象相交于、两点,则函数的图象可能是
A. B. C. D.
4、若抛物线与轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A. B. C. D.
5、已知函数,则使y=k成立的x值恰好有三个,则k的值为( )
A. 0 B. 1 C. 2 D. 3
6、已知关于的方程,存在a,是方程的两个根,则实数,n,a,的大小关系可能是
A. B. C. D.
7、如图,抛物线的对称轴为直线,若关于的一元二次方程为实数)在的范围内有解,则的取值范围是
A.﹣5<t≤4 B.3<t≤4 C.﹣5<t<3 D.t>﹣5
8、当-2≤x≤l时,二次函数有最大值4,则实数m的值为( )
A. B. 或 C.2或 D.2或或
9、二次函数的部分图象如图所示,有以下结论:①;②;③;④,其中错误结论的个数是
A.1 B.2 C.3 D.4
如图1,在菱形ABCD中,∠B=60°,动点P以每秒1个单位长度的速度自点A出发沿线段AB运动到点B,同时动点Q以每秒2个单位长度的速度自点B出发沿折线B-C- D运动到点D.图2是点P,Q运动时,△BPQ的面积S随时间t变化关系图象,则a的值是( )
A.2 B.2.5 C.3 D.2
填空题(每小题5分,共30分)
11、抛物线y=ax2与直线x=1,x=2,y=1,y=2组成的正方形有公共点,则a的取值范围是 .
12、已知二次函数,(为常数),当取不同的值时,其图象构成一个“抛物线系”.下图分别是当,,,时二次函数的图象.它们的顶点在一条直线上,这条直线的解析式是 .
13、定义符号的含义为:当a≥b时,=a;当a14、如图,一抛物线与x轴相交于A,B两点,其顶点P在折线段CD-DE上移动,已知点C,D,E的坐标分别为(一2,8),(8,8),(8,2),若点B横坐标的最小值为0,则点A横坐标的最大值为____________.
15、在平面直角坐标系中,抛物线的图象如图所示.已知A点坐标为(1,1),过点A作AA1//X轴交抛物线于点A1,过点A1,作A1A2 //OA交抛物线于点A2,过点A2作A2A3//x轴交抛物线于点A3,过点A3作A3A4 //OA交抛物线于点A4...,
依次进行下去,则点A2019的坐标为_____________.
16、我们定义一种新函数:形如y=|ax2+bx+c | (a≠0,且b2-4ac>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y= |x2-2x- - 3|的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为(一1,0),(3,0)和(0,3);②图象
具有对称性,对称轴是直线x=1;③当一1≤x≤1或x≥3时,函数值y随x值的增大而增大;④当x=-1或x=3时,函数的最小值是0;⑤当x=1时,函数的最大值是4.其中正确结论的个数是_________________.
三、解答题(共80分)
17、(8分)⑴已知函数y=mx2-6x+1(m是常数).求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)如图,抛物线y=x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.
18、(8分)已知二次函数(a为常数,).
(1)当时,求该二次函数的图象与x轴的交点个数.
(2)设,是该函数图象上的两点,其中,当时,都有,求a的取值范围.
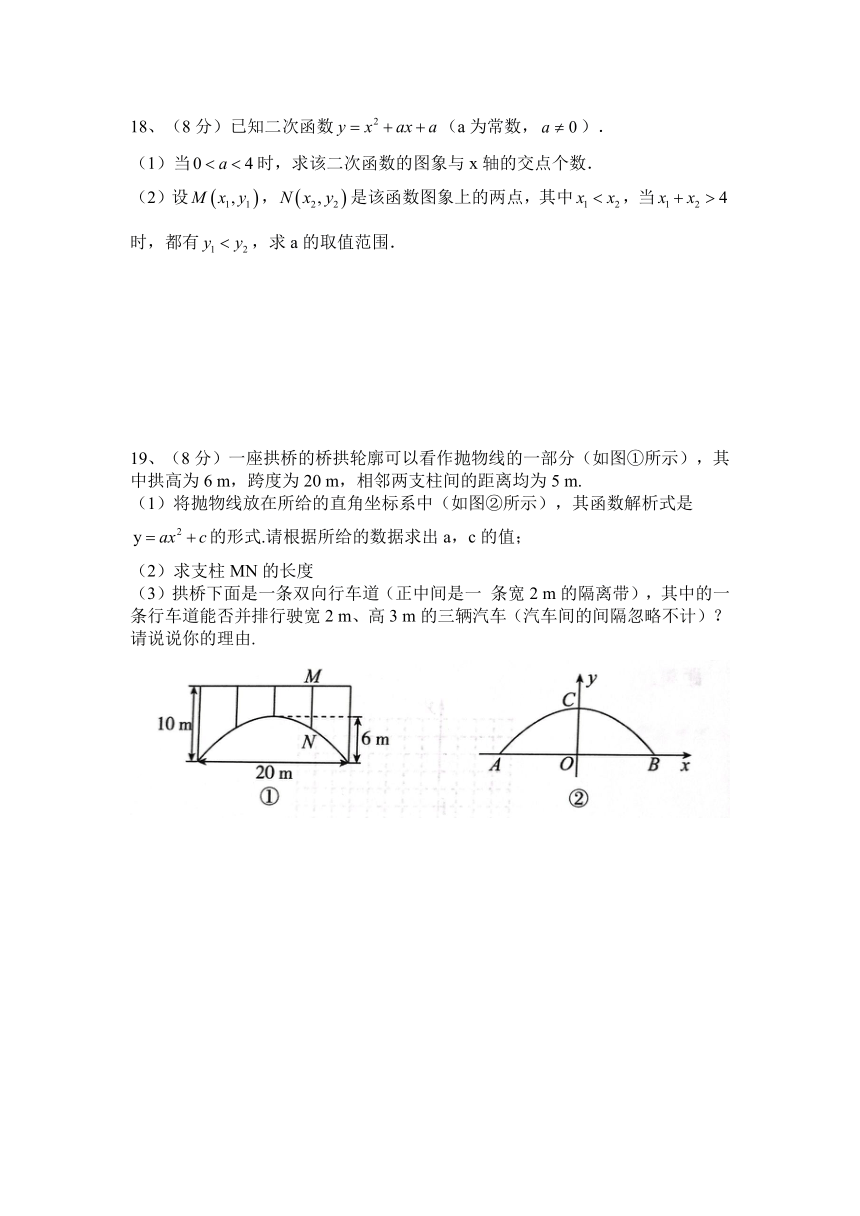
19、(8分)一座拱桥的桥拱轮廓可以看作抛物线的一部分(如图①所示),其中拱高为6 m,跨度为20 m,相邻两支柱间的距离均为5 m.
(1)将抛物线放在所给的直角坐标系中(如图②所示),其函数解析式是的形式.请根据所给的数据求出a,c的值;
(2)求支柱MN的长度
(3)拱桥下面是一条双向行车道(正中间是一 条宽2 m的隔离带),其中的一条行车道能否并排行驶宽2 m、高3 m的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由.
20、(10分)如图,在平面直角坐标系中,抛物线交x轴于A,B两点,交y轴于点C.
(1)求证:△ABC为直角三角形;
(2)直线y=m(0F.求当m为何值时,EF= DF?
(3)连结CE和BE后,对于问题“是否存在这样的点E,使△BCE的面积最大?”小红同学
认为:“当E为抛物线的顶点时,△BCE的面积最大.”她的观点是否正确?提出你的见解,若△BCE的面积存在最大值,请求出点E的坐标和△BCE的最大面积.
21、(10分)二次函数与二次函数的图象称为友好抛物线.
(1)求证:无论取何值,友好抛物线与的顶点都在某一确定的直线上.(2)若,,当时,请比较,的大小.(3)已知,,友好抛物线:,交于点,且,与轴分别交于点、点,求的值.
22、(12分)2022年北京冬奥会吉祥物“冰墩墩”万众瞩目,硅胶是生产“冰墩墩”外壳的主要原材料.某硅胶制品有限公司的两个车间负责生产“冰墩墩”硅胶外壳,已知每天生产的硅胶外壳数量甲车间是乙车间的两倍,甲车间生产8000个所用的时间比乙车间生产2000个所用的时间多一天.
(1)求出甲、乙两车间每天生产硅胶外壳个数.
(2)现有如下表所示的A,B两种型号硅胶外壳,该公司现有378千克的原材料用于生产外壳,并恰好全部用完.
型号 所需原材料 冰墩墩单价
A 99克 198元
B 90克 192元
①若生产的A,B两种型号的外壳共4000个,求出A,B两种型号的外壳个数.
②若生产的A,B两种型号的外壳若干个用于销售,且A型号的数量大于B型号的数量,则A型号外壳为多少个时,冰墩墩的销售金额最大.求出最大销售金额.
23、(12分)如图①,若抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B在抛物线L1上(点A与点B不重合),我们把这样的两抛物线L1、L2称为“伴随抛物线”,可见一条抛物线的“伴随抛物线”可以有多条.
(1)抛物线L1:y=-x2+4x-3与抛物线L2是“伴随抛物线”,且抛物线L2的顶点B的横坐标为4,求抛物线L2的表达式;
(2)若抛物线y=a1(x-m)2+n的任意一条“伴随抛物线”的表达式为y=a2(x-h)2+k,请写出a1与a2的关系式,并说明理由;
(3)在图②中,已知抛物线L1:y=mx2-2mx-3m(m>0)与y轴相交于点C,它的一条“伴随抛物线”为L2,抛物线L2与y轴相交于点D,若CD=4m,求抛物线L2的对称轴.
24、(12分)如图,已知抛物线的图象经过点,,与轴交于点,抛物线的顶点为,对称轴与轴相交于点,连接.
(1)求抛物线的解析式.
(2)在抛物线上点和点之间是否存在一点使得四边形的面积最大,若存在求出四边形的最大面积,若不存在,请说明理由.
(3)直线上有一点,使得时,过作轴于,点为轴上一动点,为直线上一动点,为抛物线上一动点,当以点,,,四点为顶点的四边形为正方形时,求点的坐标.
答案解析
B.
C.
B.
B
D
A.
B.
C.
A.
D.
12、
13、6
14、7
(-1010,10102)
4
17、(1)当x=0时,.所以不论为何值,函数的图象经过轴上的一个定点(0,1).
(2)作出点C关于x轴的对称点C′,则C′(0,2),OC′=2,连接C′D交x轴于点M,根据轴对称性及两点之间线段最短可知,MC + MD的值最小。
解法一:设抛物线的对称轴交x轴于点E.
∵ED∥y轴, ∴∠OC′M=∠EDM,∠C′OM=∠DEM
∴△C′OM∽△DEM.
∴
∴,∴m =.
解法二:设直线C′D的解析式为y = kx + n ,
则,解得n = 2, .
∴ .
∴当y = 0时, ,
. ∴.
18、(1)无交点;(2)且
19、(1)根据题意,得A,B,C的坐标分别为(-10,0),(10,0),(0,6).将点B,C的坐标代入,得解得
(2)可设点N的坐标为(5,yN),由(1)可得抛物线的函数解析式为,则.
∴支柱MN的长度为10-4.5=5.5(m).
能并排行驶宽2 m、高3 m的三辆汽车.理由如下:
如解图,设DE是隔离带的宽,EG是三辆车的宽度和,则点G的坐标为(7,0).过点G作GH⊥AB交抛物线于点H,则.
根据抛物线的特点,可知一条行车道能并排行驶三辆这样的汽车.
20、(1)证明:对于,当y=0时,,解得,;当x=0时,y=2.
∴A,B,C三点的坐标分别为A(-1,0),B(4,0),C(0,2),
∴OA=1,OB=4,OC=2,
∴AB=OA+OB=5,
∴AB2=25.在Rt△AOC中,AC2=OA2+OC2=5,在Rt△COB中,BC2=OC2+OB2=20,
∴AC2+BC2=AB2,
∴△ABC为直角三角形.
∵B(4,0),C(0,2),
∴直线BC:,∴F(m,),E(m,),
DF=,DE=,当EF=DF时,则2DF=DE,
∴4-m=,解得m1=1,m2=4.
∵0∴当m=1时,EF=DF.
小红同学的观点是错误的.
∵OD=m,DE⊥OB,E点在抛物线上,
∴E点的坐标可表示为(m,),∴DE=,
∵DF=,∴EF=DE-DF=.
∵
∴
∴当m=2时,有最大值,△BCE的面积最大为4,
∵当m=2时,=3,
∴E点的坐标为(2,3),而抛物线的顶点坐标为(),
∴小红同学的观点是错误的.
21、(1)证明:,的顶点为,
,的顶点为,设过,顶点的直线为,
把,代入得:,解得:,,
无论取何值,友好抛物线与的顶点都在直线上;
(2)解:,时,,,
令,则,解得:,,交点坐标为,
当时,,当时,,当时,;
(3),时,令,则,解得:,,
将代入,得,,,
,,.
22、(1)甲、乙车间每天生产的数量分别为4000个、2000个
(2)①生产A型号外壳2000个,B型号外壳2000个;②当A型号外壳2010个时,w有最大值,最大值为779868元
23、(1)由y=-x2+4x-3可得A的坐标为(2,1),
将x=4代入y=-x2+4x-3,得y=-3,∴B的坐标为(4,-3),
设抛物线L2的解析式为y=a(x-4)2-3; 将(2,1)代入y=a(x-4)2-3,
得1=a(2-4)2-3,解得a=1,
∴抛物线L2的表达式为y=(x-4)2-3;
(2)a1=-a2,理由如下:
∵抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B在抛物线L1上,
∴可列方程组: ,
整理,得(a1+a2)(m-h)2=0,
∵伴随抛物线的顶点不重合,∴m≠h,∴a1=-a2;
(3)抛物线L1:y=mx2-2mx-3m的顶点坐标为(1,-4m),
设抛物线L2的顶点的横坐标为h,则其纵坐标为mh2-2mh-3m,
∴抛物线L2的表达式为y=-m(x-h)2+mh2-2mh-3m,
化简得,y=-mx2+2mhx-2mh-3m,
所以点D的坐标为(0,-2mh-3m),
又点C的坐标为(0,-3m),
可得|(-2mh-3m)-(-3m)|=4m, 解得h=±2,
∴抛物线L2的对称轴为x=±2.
24、(1)∵抛物线y=x2+bx+c的图象经过点A(1,0),B(﹣3,0),
∴,
∴,
∴抛物线的解析式为y=x2+2x﹣3;
(2)当x=﹣1时,y=﹣4,所以点D(﹣1,﹣4)
当x=0时,y=﹣3,所以点C(0.﹣3)
设点H(a,a2+2a﹣3)(﹣3<a<﹣1)
所以S四边形OBHC=S△OBH+S△OCH
=OB×|a2+2a﹣3|+OC×|a|
=(3﹣2a﹣a2)﹣a
=﹣a2﹣+
当a=﹣=﹣时,S四边形OBHC=.
(3)由(1)知,抛物线的解析式为y=x2+2x﹣3;
∴C(0,﹣3),抛物线的顶点D(﹣1,﹣4),
∴E(﹣1,0),
设直线BD的解析式为y=mx+n,
∴,
∴,
∴直线BD的解析式为y=﹣2x﹣6,
设点P(m,﹣2m﹣6),
∵C(0,﹣3),E(﹣1,0),
根据勾股定理得,PE2=(m+1)2+(﹣2m﹣6)2,PC2=m2+(﹣2m﹣6+3)2,
∵PC=PE,
∴(m+1)2+(﹣2m﹣6)2=m2+(﹣2m﹣6+3)2,
∴m=﹣2,
∴y=﹣2×(﹣2)﹣6=﹣2,
∴P(﹣2,﹣2),
如图,作PF⊥x轴于F,
∴F(﹣2,0),
设M(d,0),
∴G(d,d2+2d﹣3),N(﹣2,d2+2d﹣3),
∵以点F,N,G,M四点为顶点的四边形为正方形,必有FM=MG,
∴|d+2|=|d2+2d﹣3|,
∴d=或d=,
∴点M的坐标为(,0),(,0),(,0),(,0).
选择题(每小题4分,共40分)
1、已知函数,其图象是抛物线, 则的取值是
A . B . C . D .
2、已知抛物线过,,,四点,则与的大小关系是
A. B. C. D.不能确定
3、如图,一次函数与二次函数图象相交于、两点,则函数的图象可能是
A. B. C. D.
4、若抛物线与轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A. B. C. D.
5、已知函数,则使y=k成立的x值恰好有三个,则k的值为( )
A. 0 B. 1 C. 2 D. 3
6、已知关于的方程,存在a,是方程的两个根,则实数,n,a,的大小关系可能是
A. B. C. D.
7、如图,抛物线的对称轴为直线,若关于的一元二次方程为实数)在的范围内有解,则的取值范围是
A.﹣5<t≤4 B.3<t≤4 C.﹣5<t<3 D.t>﹣5
8、当-2≤x≤l时,二次函数有最大值4,则实数m的值为( )
A. B. 或 C.2或 D.2或或
9、二次函数的部分图象如图所示,有以下结论:①;②;③;④,其中错误结论的个数是
A.1 B.2 C.3 D.4
如图1,在菱形ABCD中,∠B=60°,动点P以每秒1个单位长度的速度自点A出发沿线段AB运动到点B,同时动点Q以每秒2个单位长度的速度自点B出发沿折线B-C- D运动到点D.图2是点P,Q运动时,△BPQ的面积S随时间t变化关系图象,则a的值是( )
A.2 B.2.5 C.3 D.2
填空题(每小题5分,共30分)
11、抛物线y=ax2与直线x=1,x=2,y=1,y=2组成的正方形有公共点,则a的取值范围是 .
12、已知二次函数,(为常数),当取不同的值时,其图象构成一个“抛物线系”.下图分别是当,,,时二次函数的图象.它们的顶点在一条直线上,这条直线的解析式是 .
13、定义符号的含义为:当a≥b时,=a;当a
15、在平面直角坐标系中,抛物线的图象如图所示.已知A点坐标为(1,1),过点A作AA1//X轴交抛物线于点A1,过点A1,作A1A2 //OA交抛物线于点A2,过点A2作A2A3//x轴交抛物线于点A3,过点A3作A3A4 //OA交抛物线于点A4...,
依次进行下去,则点A2019的坐标为_____________.
16、我们定义一种新函数:形如y=|ax2+bx+c | (a≠0,且b2-4ac>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y= |x2-2x- - 3|的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为(一1,0),(3,0)和(0,3);②图象
具有对称性,对称轴是直线x=1;③当一1≤x≤1或x≥3时,函数值y随x值的增大而增大;④当x=-1或x=3时,函数的最小值是0;⑤当x=1时,函数的最大值是4.其中正确结论的个数是_________________.
三、解答题(共80分)
17、(8分)⑴已知函数y=mx2-6x+1(m是常数).求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)如图,抛物线y=x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.
18、(8分)已知二次函数(a为常数,).
(1)当时,求该二次函数的图象与x轴的交点个数.
(2)设,是该函数图象上的两点,其中,当时,都有,求a的取值范围.
19、(8分)一座拱桥的桥拱轮廓可以看作抛物线的一部分(如图①所示),其中拱高为6 m,跨度为20 m,相邻两支柱间的距离均为5 m.
(1)将抛物线放在所给的直角坐标系中(如图②所示),其函数解析式是的形式.请根据所给的数据求出a,c的值;
(2)求支柱MN的长度
(3)拱桥下面是一条双向行车道(正中间是一 条宽2 m的隔离带),其中的一条行车道能否并排行驶宽2 m、高3 m的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由.
20、(10分)如图,在平面直角坐标系中,抛物线交x轴于A,B两点,交y轴于点C.
(1)求证:△ABC为直角三角形;
(2)直线y=m(0
(3)连结CE和BE后,对于问题“是否存在这样的点E,使△BCE的面积最大?”小红同学
认为:“当E为抛物线的顶点时,△BCE的面积最大.”她的观点是否正确?提出你的见解,若△BCE的面积存在最大值,请求出点E的坐标和△BCE的最大面积.
21、(10分)二次函数与二次函数的图象称为友好抛物线.
(1)求证:无论取何值,友好抛物线与的顶点都在某一确定的直线上.(2)若,,当时,请比较,的大小.(3)已知,,友好抛物线:,交于点,且,与轴分别交于点、点,求的值.
22、(12分)2022年北京冬奥会吉祥物“冰墩墩”万众瞩目,硅胶是生产“冰墩墩”外壳的主要原材料.某硅胶制品有限公司的两个车间负责生产“冰墩墩”硅胶外壳,已知每天生产的硅胶外壳数量甲车间是乙车间的两倍,甲车间生产8000个所用的时间比乙车间生产2000个所用的时间多一天.
(1)求出甲、乙两车间每天生产硅胶外壳个数.
(2)现有如下表所示的A,B两种型号硅胶外壳,该公司现有378千克的原材料用于生产外壳,并恰好全部用完.
型号 所需原材料 冰墩墩单价
A 99克 198元
B 90克 192元
①若生产的A,B两种型号的外壳共4000个,求出A,B两种型号的外壳个数.
②若生产的A,B两种型号的外壳若干个用于销售,且A型号的数量大于B型号的数量,则A型号外壳为多少个时,冰墩墩的销售金额最大.求出最大销售金额.
23、(12分)如图①,若抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B在抛物线L1上(点A与点B不重合),我们把这样的两抛物线L1、L2称为“伴随抛物线”,可见一条抛物线的“伴随抛物线”可以有多条.
(1)抛物线L1:y=-x2+4x-3与抛物线L2是“伴随抛物线”,且抛物线L2的顶点B的横坐标为4,求抛物线L2的表达式;
(2)若抛物线y=a1(x-m)2+n的任意一条“伴随抛物线”的表达式为y=a2(x-h)2+k,请写出a1与a2的关系式,并说明理由;
(3)在图②中,已知抛物线L1:y=mx2-2mx-3m(m>0)与y轴相交于点C,它的一条“伴随抛物线”为L2,抛物线L2与y轴相交于点D,若CD=4m,求抛物线L2的对称轴.
24、(12分)如图,已知抛物线的图象经过点,,与轴交于点,抛物线的顶点为,对称轴与轴相交于点,连接.
(1)求抛物线的解析式.
(2)在抛物线上点和点之间是否存在一点使得四边形的面积最大,若存在求出四边形的最大面积,若不存在,请说明理由.
(3)直线上有一点,使得时,过作轴于,点为轴上一动点,为直线上一动点,为抛物线上一动点,当以点,,,四点为顶点的四边形为正方形时,求点的坐标.
答案解析
B.
C.
B.
B
D
A.
B.
C.
A.
D.
12、
13、6
14、7
(-1010,10102)
4
17、(1)当x=0时,.所以不论为何值,函数的图象经过轴上的一个定点(0,1).
(2)作出点C关于x轴的对称点C′,则C′(0,2),OC′=2,连接C′D交x轴于点M,根据轴对称性及两点之间线段最短可知,MC + MD的值最小。
解法一:设抛物线的对称轴交x轴于点E.
∵ED∥y轴, ∴∠OC′M=∠EDM,∠C′OM=∠DEM
∴△C′OM∽△DEM.
∴
∴,∴m =.
解法二:设直线C′D的解析式为y = kx + n ,
则,解得n = 2, .
∴ .
∴当y = 0时, ,
. ∴.
18、(1)无交点;(2)且
19、(1)根据题意,得A,B,C的坐标分别为(-10,0),(10,0),(0,6).将点B,C的坐标代入,得解得
(2)可设点N的坐标为(5,yN),由(1)可得抛物线的函数解析式为,则.
∴支柱MN的长度为10-4.5=5.5(m).
能并排行驶宽2 m、高3 m的三辆汽车.理由如下:
如解图,设DE是隔离带的宽,EG是三辆车的宽度和,则点G的坐标为(7,0).过点G作GH⊥AB交抛物线于点H,则.
根据抛物线的特点,可知一条行车道能并排行驶三辆这样的汽车.
20、(1)证明:对于,当y=0时,,解得,;当x=0时,y=2.
∴A,B,C三点的坐标分别为A(-1,0),B(4,0),C(0,2),
∴OA=1,OB=4,OC=2,
∴AB=OA+OB=5,
∴AB2=25.在Rt△AOC中,AC2=OA2+OC2=5,在Rt△COB中,BC2=OC2+OB2=20,
∴AC2+BC2=AB2,
∴△ABC为直角三角形.
∵B(4,0),C(0,2),
∴直线BC:,∴F(m,),E(m,),
DF=,DE=,当EF=DF时,则2DF=DE,
∴4-m=,解得m1=1,m2=4.
∵0
小红同学的观点是错误的.
∵OD=m,DE⊥OB,E点在抛物线上,
∴E点的坐标可表示为(m,),∴DE=,
∵DF=,∴EF=DE-DF=.
∵
∴
∴当m=2时,有最大值,△BCE的面积最大为4,
∵当m=2时,=3,
∴E点的坐标为(2,3),而抛物线的顶点坐标为(),
∴小红同学的观点是错误的.
21、(1)证明:,的顶点为,
,的顶点为,设过,顶点的直线为,
把,代入得:,解得:,,
无论取何值,友好抛物线与的顶点都在直线上;
(2)解:,时,,,
令,则,解得:,,交点坐标为,
当时,,当时,,当时,;
(3),时,令,则,解得:,,
将代入,得,,,
,,.
22、(1)甲、乙车间每天生产的数量分别为4000个、2000个
(2)①生产A型号外壳2000个,B型号外壳2000个;②当A型号外壳2010个时,w有最大值,最大值为779868元
23、(1)由y=-x2+4x-3可得A的坐标为(2,1),
将x=4代入y=-x2+4x-3,得y=-3,∴B的坐标为(4,-3),
设抛物线L2的解析式为y=a(x-4)2-3; 将(2,1)代入y=a(x-4)2-3,
得1=a(2-4)2-3,解得a=1,
∴抛物线L2的表达式为y=(x-4)2-3;
(2)a1=-a2,理由如下:
∵抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B在抛物线L1上,
∴可列方程组: ,
整理,得(a1+a2)(m-h)2=0,
∵伴随抛物线的顶点不重合,∴m≠h,∴a1=-a2;
(3)抛物线L1:y=mx2-2mx-3m的顶点坐标为(1,-4m),
设抛物线L2的顶点的横坐标为h,则其纵坐标为mh2-2mh-3m,
∴抛物线L2的表达式为y=-m(x-h)2+mh2-2mh-3m,
化简得,y=-mx2+2mhx-2mh-3m,
所以点D的坐标为(0,-2mh-3m),
又点C的坐标为(0,-3m),
可得|(-2mh-3m)-(-3m)|=4m, 解得h=±2,
∴抛物线L2的对称轴为x=±2.
24、(1)∵抛物线y=x2+bx+c的图象经过点A(1,0),B(﹣3,0),
∴,
∴,
∴抛物线的解析式为y=x2+2x﹣3;
(2)当x=﹣1时,y=﹣4,所以点D(﹣1,﹣4)
当x=0时,y=﹣3,所以点C(0.﹣3)
设点H(a,a2+2a﹣3)(﹣3<a<﹣1)
所以S四边形OBHC=S△OBH+S△OCH
=OB×|a2+2a﹣3|+OC×|a|
=(3﹣2a﹣a2)﹣a
=﹣a2﹣+
当a=﹣=﹣时,S四边形OBHC=.
(3)由(1)知,抛物线的解析式为y=x2+2x﹣3;
∴C(0,﹣3),抛物线的顶点D(﹣1,﹣4),
∴E(﹣1,0),
设直线BD的解析式为y=mx+n,
∴,
∴,
∴直线BD的解析式为y=﹣2x﹣6,
设点P(m,﹣2m﹣6),
∵C(0,﹣3),E(﹣1,0),
根据勾股定理得,PE2=(m+1)2+(﹣2m﹣6)2,PC2=m2+(﹣2m﹣6+3)2,
∵PC=PE,
∴(m+1)2+(﹣2m﹣6)2=m2+(﹣2m﹣6+3)2,
∴m=﹣2,
∴y=﹣2×(﹣2)﹣6=﹣2,
∴P(﹣2,﹣2),
如图,作PF⊥x轴于F,
∴F(﹣2,0),
设M(d,0),
∴G(d,d2+2d﹣3),N(﹣2,d2+2d﹣3),
∵以点F,N,G,M四点为顶点的四边形为正方形,必有FM=MG,
∴|d+2|=|d2+2d﹣3|,
∴d=或d=,
∴点M的坐标为(,0),(,0),(,0),(,0).
同课章节目录
