北京市陈经纶中学分校2025年中考数学零模试卷(pdf版,无答案)
文档属性
| 名称 | 北京市陈经纶中学分校2025年中考数学零模试卷(pdf版,无答案) |  | |
| 格式 | |||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 21:05:52 | ||
图片预览


文档简介
北京市陈经纶中学分校
2024-2025 学年第二学期零模检测
数学试卷 2025.4
一、选择题(本题共 16 分,每小题 2 分)
1. 下列图形都是轴对称图形,其中恰有 2条对称轴的图形是
A. B. C. D
2. 实数 a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是
A. a c B.bc 0 C.a d 0 D.b 2
3. 在一个不透明的盒子中装有 4个白球,其余为黄球,它们除颜色不同外,其余都相同,
1
若从中随机摸出一个球,颜色是白球的概率为 ,则黄球的个数是
4
A. 8 B. 10 C. 16 D. 12
4. 两个直角三角板如图放置,其中∠BAC =∠DAE = 90 ,∠B= 45 ,
∠D= 60 ,若 E点在 BC边上,DE的中点 F恰好落在 AC边上,则下
列三角形是等腰三角形的是
A.△ABE B.△AEF C.△AEC D.△CEF
5. 长江经济带覆盖上海、湖南、云南、贵州等 11省市,面积约 2 050 000 平方公里,约占
全国面积的 21% .将 2 050 000 用科学记数法表示应为
A. 205万 B. 205 104 C. 2.05 106 D. 2.05 107
6.如图,已知锐角∠AOB
(1)在射线 OA上取一点 C,以点 O为圆心,OC长为半径作 ,
交射线 OB于点 D,连接 CD;
(2)分别以点 C,D为圆心,CD长为半径作弧,交 于点 M,N;
(3)连接 OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是
A. MN∥CD B. ME=EF=EN C . ∠CMN=∠DNM D. ∠MCO=∠MFO
九年级模拟测试数学试卷第 1页(共 6页)
7.在一次男子马拉松比赛中,随机抽取了 10名选手,记录他们的成绩(所用的时间)如下:
选手 1 2 3 4 5 6 7 8 9 10
时间(min) 129 136 140 145 146 148 154 158 165 175
由此所得的以下推断不.正.确.的是
A.这组样本数据的平均数超过 130;
B.这组样本数据的中位数是 147;
C.在这次比赛中,估计成绩为 130 min的选手的成绩会比平均成绩差;
D.在这次比赛中,估计成绩为 142 min的选手,会比一半以上的选手成绩要好.
8.已知△ABC的两条中线 AD与 BE交于点 G,连接 CG。
若 BG⊥CG,BC=2, 下列四个结论正确的是:
○1 AG=2 ○2 AC的最小值是 2 2
○3 △ABC的面积最大值是 3. ○4 AC +AB =20
A. ○1 ○2 B. ○1 ○3 C. ○1 ○2 ○4 D. ○1 ○3 ○4
二、填空题(本题共 16分,每小题 2分)
9. 如图所示,a∥b,直线 a与直线 b之间的距离是线段_______的长度
x
10. 若分式 2 的值为正,则实数 x的取值范围是__________________.x 2
11. 在平面直角坐标系 xOy中,点 A a,b a 0,b 0 在双曲线 y k 1 上.
x
点 A关于 x轴的对称点B在双曲线 y k 2 上,则k k 的值为 ______ .
x 1 2
12. 为了说明命题“对于实数 m,若(m-2)2>0,则 m>2”是错误的,m的值可以是______
13. 2小天想要计算一组数据92,90,94,86,99,85的方差 s0 .在计算平均数的过程中,
将这组数据中的每一个数都减去90,得到一组新数据2,0,4, 4,9, 5.记这组新
s2 2数据的方差为 1 ,则 s1 ______ s
2
0 . (填“ ”,“ ”或“ ”)
14.在矩形 ABCD中,M,N,P,Q分别为边 AB,BC,CD,DA上的点(不与端点重合).
对于任意矩形 ABCD,下面四个结论中,
①存在无数个四边形 MNPQ是平行四边形;②存在无数个四边形 MNPQ是矩形;
③存在无数个四边形 MNPQ是菱形; ④至少存在一个四边形 MNPQ是正方形.
所有正确结论的序号是 ______.
九年级模拟测试数学试卷第 2页(共 6页)
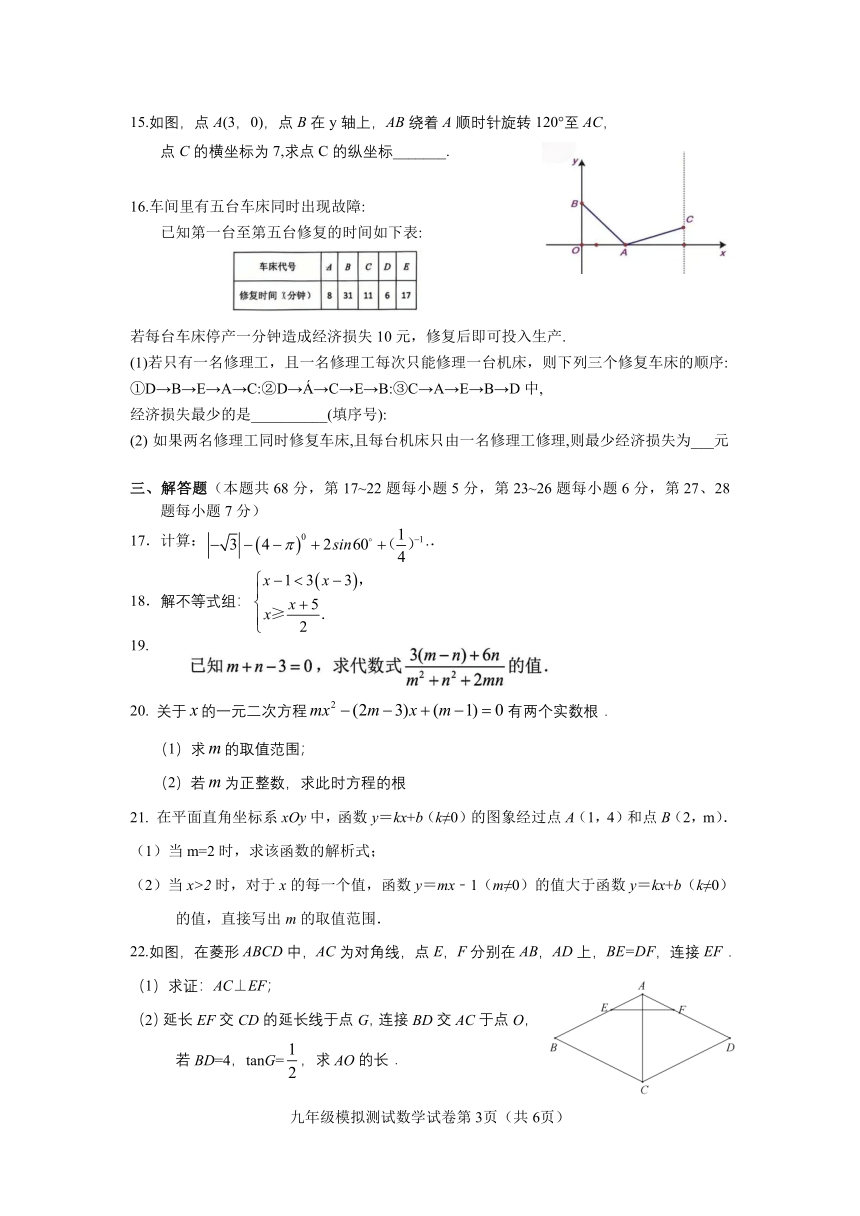
15.如图,点 A(3,0),点 B在 y 轴上,AB绕着 A顺时针旋转 120°至 AC,
点 C的横坐标为 7,求点 C 的纵坐标_______.
16.车间里有五台车床同时出现故障:
已知第一台至第五台修复的时间如下表:
若每台车床停产一分钟造成经济损失 10元,修复后即可投入生产.
(1)若只有一名修理工,且一名修理工每次只能修理一台机床,则下列三个修复车床的顺序:
①D→B→E→A→C:②D→ →C→E→B:③C→A→E→B→D中,
经济损失最少的是__________(填序号):
(2) 如果两名修理工同时修复车床,且每台机床只由一名修理工修理,则最少经济损失为___元
三、解答题(本题共 68 分,第 17~22 题每小题 5 分,第 23~26 题每小题 6 分,第 27、28
题每小题 7分)
17.计算: 3 4 0 2sin60 1 ( ) 1 ..
4
x 1 3 x 3 ,
18 .解不等式组:
x x 5 ≥ . 2
19.
20. 关于 x的一元二次方程mx2 (2m 3)x (m 1) 0有两个实数根.
(1)求m的取值范围;
(2)若m为正整数,求此时方程的根
21. 在平面直角坐标系 xOy中,函数 y=kx+b(k≠0)的图象经过点 A(1,4)和点 B(2,m).
(1)当 m=2时,求该函数的解析式;
(2)当 x>2时,对于 x的每一个值,函数 y=mx﹣1(m≠0)的值大于函数 y=kx+b(k≠0)
的值,直接写出 m的取值范围.
22.如图,在菱形 ABCD中,AC为对角线,点 E,F分别在 AB,AD上,BE=DF,连接 EF.
(1)求证:AC⊥EF;
(2)延长 EF交 CD的延长线于点 G,连接 BD交 AC于点 O,
1
若 BD=4,tanG= ,求 AO的长.
2
九年级模拟测试数学试卷第 3页(共 6页)
23.某机器工作至电量剩余 10%时开始充电.充电系统提供两种不同的充电模式,机器剩余电
量 Y(单位:%)与充电时间 t(单位:min)的关系如下表所示:
(1)①m=_________;
②通过数据分析,发现可以用函数来刻画 Y 与 t,Y 与 t之间的关系,在给定的平面直角坐标
系(图 1)中画出这两个函数图象;
(3) 充电系统通过调节充电电流 I(单位:安培 A)来控制电量,已知充电模式一的初始电流为
10安培,剩余电量每增加 10%,充电电流将减小 0.5安培,则 10分钟时充电模式一的充电电
流 I=___安培;充电模式二的充电电流与充电时间的函数关系如图 2所示.根据以上数据并结
合函数图象判断:当两种充电模式的电流相同时,剩余电量相差约_____%.
24. 2025年春节,《哪吒之魔童闹海》(以下简称《哪吒 2》)横空出世,现已登顶全球动画
电影票房榜,小果同学为了了解这部电影在同学中的受欢迎程度,在初三年级随机抽取了
10名男生和 10名女生展开问卷调查(问卷调查满分为 100分),并对数据进行整理,描述
和分析(评分分数用 x表示,共分为四组:A. x<70;B.70≤x<8;C.80≤x<90;D.90≤x≤100)
下面给出了部分信息:
10名女生对《哪吒2》的评分分数:
67, 77, 79, 83, 89, 91, 98, 98, 98, 100.
10名男生对《哪吒2》的评分分数在C组的数据是:82,83,86.
九年级模拟测试数学试卷第 4页(共 6页)
10名男生对《哪吒 2》评分扇形统计图
20名同学对《哪吒2》评分统计表
性别 平均数 众数 中位数 方差 满分占比
女生 88 a 90 112.2 10%
男生 88 100 b 200.2 50%
根据以上信息,解答下列问题:
(1)上述图表中的a=______,b=_____,m=_____;
( 2)根据以上数据分析,你认为是女生更喜欢《哪吒2》还是男生更喜欢?请说明理由;
(写出一条理由即可)
( 3)我校初三年级有400名女生和500名男生去看过《哪吒2》,估计这些学生中对《哪
吒2》的评分在D组共有多少人?
25. 如图,△ABC 内接于☉O ,作 AD⊥CB 于 D,与☉O 交于点 E,点 F在 DA的延长线
上,使得∠FCA =∠ABC=α.
(1)求证:CF是☉O 的切线;
(2) tanα= 3若 ,BE=8,求☉O的半径长.
4
26. 已知抛物线 y=a(x-h)2-12a+2.
(1)若 a= -1,求抛物线与 x 轴的两个交点之间的距离;
(2)已知点 C(h,5)和点 P(m.n)是抛物线上的两点.
○1 求出 a的值;
○2 若对于任意的-2≤k≤ 4,直线 y=kx 与抛物线有两个交点 A(x1, y1),B(x2, y2),3
且当 x1九年级模拟测试数学试卷第 5页(共 6页)
27. 在△ABC 中,已知∠ACB=α(0°<α<180°),以点 B为中心,将线段 AB 逆时针旋转α得
到线段 BD,连接 CD.
(1)如图 1,当α=90°时,若 AB=CD,求 sin∠BAC 的值:
(2)如图 2,当α=120°时,点 E 为 CD中点,连接 BE.
①依题意补全图形;
②用等式表示线段 AC,BC,BE 的数量关系,并证明.
图 1 图 2
28. 对于平面直角坐标系 xOy中的点 P与⊙C,若将点 P绕着点 C旋转α(0°<α<180°)得
到点 Q,直线 PQ刚好与⊙C相切,则称点 P为⊙C的“α旋切点”.
(1)若α=60° O 2 3 3,⊙ 半径为 1. 在点 P1(-2,0),P2(0, ),P3 3( 1, )中,3
点 ______ 是⊙O的“60°旋切点”;
(2)已知点 M(1, 3)在⊙O上.
若点 N为⊙O的“120°旋切点”,且MN=2 5,求点 N的坐标;
(3)已知点 A(﹣4,0),B(0,3),C(0,t),若线段 AB上每个点都是⊙C的“α旋切
点”,且 0<α≤120°,直接写出 t的取值范围.
九年级模拟测试数学试卷第 6页(共 6页)
2024-2025 学年第二学期零模检测
数学试卷 2025.4
一、选择题(本题共 16 分,每小题 2 分)
1. 下列图形都是轴对称图形,其中恰有 2条对称轴的图形是
A. B. C. D
2. 实数 a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是
A. a c B.bc 0 C.a d 0 D.b 2
3. 在一个不透明的盒子中装有 4个白球,其余为黄球,它们除颜色不同外,其余都相同,
1
若从中随机摸出一个球,颜色是白球的概率为 ,则黄球的个数是
4
A. 8 B. 10 C. 16 D. 12
4. 两个直角三角板如图放置,其中∠BAC =∠DAE = 90 ,∠B= 45 ,
∠D= 60 ,若 E点在 BC边上,DE的中点 F恰好落在 AC边上,则下
列三角形是等腰三角形的是
A.△ABE B.△AEF C.△AEC D.△CEF
5. 长江经济带覆盖上海、湖南、云南、贵州等 11省市,面积约 2 050 000 平方公里,约占
全国面积的 21% .将 2 050 000 用科学记数法表示应为
A. 205万 B. 205 104 C. 2.05 106 D. 2.05 107
6.如图,已知锐角∠AOB
(1)在射线 OA上取一点 C,以点 O为圆心,OC长为半径作 ,
交射线 OB于点 D,连接 CD;
(2)分别以点 C,D为圆心,CD长为半径作弧,交 于点 M,N;
(3)连接 OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是
A. MN∥CD B. ME=EF=EN C . ∠CMN=∠DNM D. ∠MCO=∠MFO
九年级模拟测试数学试卷第 1页(共 6页)
7.在一次男子马拉松比赛中,随机抽取了 10名选手,记录他们的成绩(所用的时间)如下:
选手 1 2 3 4 5 6 7 8 9 10
时间(min) 129 136 140 145 146 148 154 158 165 175
由此所得的以下推断不.正.确.的是
A.这组样本数据的平均数超过 130;
B.这组样本数据的中位数是 147;
C.在这次比赛中,估计成绩为 130 min的选手的成绩会比平均成绩差;
D.在这次比赛中,估计成绩为 142 min的选手,会比一半以上的选手成绩要好.
8.已知△ABC的两条中线 AD与 BE交于点 G,连接 CG。
若 BG⊥CG,BC=2, 下列四个结论正确的是:
○1 AG=2 ○2 AC的最小值是 2 2
○3 △ABC的面积最大值是 3. ○4 AC +AB =20
A. ○1 ○2 B. ○1 ○3 C. ○1 ○2 ○4 D. ○1 ○3 ○4
二、填空题(本题共 16分,每小题 2分)
9. 如图所示,a∥b,直线 a与直线 b之间的距离是线段_______的长度
x
10. 若分式 2 的值为正,则实数 x的取值范围是__________________.x 2
11. 在平面直角坐标系 xOy中,点 A a,b a 0,b 0 在双曲线 y k 1 上.
x
点 A关于 x轴的对称点B在双曲线 y k 2 上,则k k 的值为 ______ .
x 1 2
12. 为了说明命题“对于实数 m,若(m-2)2>0,则 m>2”是错误的,m的值可以是______
13. 2小天想要计算一组数据92,90,94,86,99,85的方差 s0 .在计算平均数的过程中,
将这组数据中的每一个数都减去90,得到一组新数据2,0,4, 4,9, 5.记这组新
s2 2数据的方差为 1 ,则 s1 ______ s
2
0 . (填“ ”,“ ”或“ ”)
14.在矩形 ABCD中,M,N,P,Q分别为边 AB,BC,CD,DA上的点(不与端点重合).
对于任意矩形 ABCD,下面四个结论中,
①存在无数个四边形 MNPQ是平行四边形;②存在无数个四边形 MNPQ是矩形;
③存在无数个四边形 MNPQ是菱形; ④至少存在一个四边形 MNPQ是正方形.
所有正确结论的序号是 ______.
九年级模拟测试数学试卷第 2页(共 6页)
15.如图,点 A(3,0),点 B在 y 轴上,AB绕着 A顺时针旋转 120°至 AC,
点 C的横坐标为 7,求点 C 的纵坐标_______.
16.车间里有五台车床同时出现故障:
已知第一台至第五台修复的时间如下表:
若每台车床停产一分钟造成经济损失 10元,修复后即可投入生产.
(1)若只有一名修理工,且一名修理工每次只能修理一台机床,则下列三个修复车床的顺序:
①D→B→E→A→C:②D→ →C→E→B:③C→A→E→B→D中,
经济损失最少的是__________(填序号):
(2) 如果两名修理工同时修复车床,且每台机床只由一名修理工修理,则最少经济损失为___元
三、解答题(本题共 68 分,第 17~22 题每小题 5 分,第 23~26 题每小题 6 分,第 27、28
题每小题 7分)
17.计算: 3 4 0 2sin60 1 ( ) 1 ..
4
x 1 3 x 3 ,
18 .解不等式组:
x x 5 ≥ . 2
19.
20. 关于 x的一元二次方程mx2 (2m 3)x (m 1) 0有两个实数根.
(1)求m的取值范围;
(2)若m为正整数,求此时方程的根
21. 在平面直角坐标系 xOy中,函数 y=kx+b(k≠0)的图象经过点 A(1,4)和点 B(2,m).
(1)当 m=2时,求该函数的解析式;
(2)当 x>2时,对于 x的每一个值,函数 y=mx﹣1(m≠0)的值大于函数 y=kx+b(k≠0)
的值,直接写出 m的取值范围.
22.如图,在菱形 ABCD中,AC为对角线,点 E,F分别在 AB,AD上,BE=DF,连接 EF.
(1)求证:AC⊥EF;
(2)延长 EF交 CD的延长线于点 G,连接 BD交 AC于点 O,
1
若 BD=4,tanG= ,求 AO的长.
2
九年级模拟测试数学试卷第 3页(共 6页)
23.某机器工作至电量剩余 10%时开始充电.充电系统提供两种不同的充电模式,机器剩余电
量 Y(单位:%)与充电时间 t(单位:min)的关系如下表所示:
(1)①m=_________;
②通过数据分析,发现可以用函数来刻画 Y 与 t,Y 与 t之间的关系,在给定的平面直角坐标
系(图 1)中画出这两个函数图象;
(3) 充电系统通过调节充电电流 I(单位:安培 A)来控制电量,已知充电模式一的初始电流为
10安培,剩余电量每增加 10%,充电电流将减小 0.5安培,则 10分钟时充电模式一的充电电
流 I=___安培;充电模式二的充电电流与充电时间的函数关系如图 2所示.根据以上数据并结
合函数图象判断:当两种充电模式的电流相同时,剩余电量相差约_____%.
24. 2025年春节,《哪吒之魔童闹海》(以下简称《哪吒 2》)横空出世,现已登顶全球动画
电影票房榜,小果同学为了了解这部电影在同学中的受欢迎程度,在初三年级随机抽取了
10名男生和 10名女生展开问卷调查(问卷调查满分为 100分),并对数据进行整理,描述
和分析(评分分数用 x表示,共分为四组:A. x<70;B.70≤x<8;C.80≤x<90;D.90≤x≤100)
下面给出了部分信息:
10名女生对《哪吒2》的评分分数:
67, 77, 79, 83, 89, 91, 98, 98, 98, 100.
10名男生对《哪吒2》的评分分数在C组的数据是:82,83,86.
九年级模拟测试数学试卷第 4页(共 6页)
10名男生对《哪吒 2》评分扇形统计图
20名同学对《哪吒2》评分统计表
性别 平均数 众数 中位数 方差 满分占比
女生 88 a 90 112.2 10%
男生 88 100 b 200.2 50%
根据以上信息,解答下列问题:
(1)上述图表中的a=______,b=_____,m=_____;
( 2)根据以上数据分析,你认为是女生更喜欢《哪吒2》还是男生更喜欢?请说明理由;
(写出一条理由即可)
( 3)我校初三年级有400名女生和500名男生去看过《哪吒2》,估计这些学生中对《哪
吒2》的评分在D组共有多少人?
25. 如图,△ABC 内接于☉O ,作 AD⊥CB 于 D,与☉O 交于点 E,点 F在 DA的延长线
上,使得∠FCA =∠ABC=α.
(1)求证:CF是☉O 的切线;
(2) tanα= 3若 ,BE=8,求☉O的半径长.
4
26. 已知抛物线 y=a(x-h)2-12a+2.
(1)若 a= -1,求抛物线与 x 轴的两个交点之间的距离;
(2)已知点 C(h,5)和点 P(m.n)是抛物线上的两点.
○1 求出 a的值;
○2 若对于任意的-2≤k≤ 4,直线 y=kx 与抛物线有两个交点 A(x1, y1),B(x2, y2),3
且当 x1
27. 在△ABC 中,已知∠ACB=α(0°<α<180°),以点 B为中心,将线段 AB 逆时针旋转α得
到线段 BD,连接 CD.
(1)如图 1,当α=90°时,若 AB=CD,求 sin∠BAC 的值:
(2)如图 2,当α=120°时,点 E 为 CD中点,连接 BE.
①依题意补全图形;
②用等式表示线段 AC,BC,BE 的数量关系,并证明.
图 1 图 2
28. 对于平面直角坐标系 xOy中的点 P与⊙C,若将点 P绕着点 C旋转α(0°<α<180°)得
到点 Q,直线 PQ刚好与⊙C相切,则称点 P为⊙C的“α旋切点”.
(1)若α=60° O 2 3 3,⊙ 半径为 1. 在点 P1(-2,0),P2(0, ),P3 3( 1, )中,3
点 ______ 是⊙O的“60°旋切点”;
(2)已知点 M(1, 3)在⊙O上.
若点 N为⊙O的“120°旋切点”,且MN=2 5,求点 N的坐标;
(3)已知点 A(﹣4,0),B(0,3),C(0,t),若线段 AB上每个点都是⊙C的“α旋切
点”,且 0<α≤120°,直接写出 t的取值范围.
九年级模拟测试数学试卷第 6页(共 6页)
同课章节目录
