8.6.1 直线与直线垂直 课件(共22张PPT)-2024-2025学年高一数学(人教A版2019必修第二册)
文档属性
| 名称 | 8.6.1 直线与直线垂直 课件(共22张PPT)-2024-2025学年高一数学(人教A版2019必修第二册) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-22 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
第八章立体几何初步
人教A版2019必修第二册
8.6.1 直线与直线垂直
理解异面直线所成角的定义,并能做出异面直线的角
理解两条直线垂直的定义
通过实例,解决直线与直线平行的相关问题
学习目标
1
在同一平面内,有且只有一个公共点 .
共面直线
在同一平面内,没有公共点 .
异面直线 不同在任何一个平面内,没 有公共点 .
b β \b
b
a
α
在初中我们已经研究了平行直线和相交直线.本节我们主要研究异面 直线,首先研究如何刻画两条异面直线的位置关系.
空间两条直线的位置关系
相交直线
平行直线
y 复习回顾
a
图中的角θ即为直线a与直线b的夹角.
范围:[0,
规定:如果两条直线平行或重合,它们的夹角为0.
追问空间中两条直线所成角又该如何定义 它的范围又是多少
问题1平面中,两条相交直线形成几个角 两直线夹角的取值范围是多少
平面内两条直线相交形成4个角,其中不大于90°的角称为这两条直线
所成的角(或夹角) ,它刻画了一条直线相对于另一条直线倾斜的程度.
y 新知探究
问题2 如图示,在正方体ABCD-A'B'C'D '中,直线A'C 与直线AB, 直线A'D'
与直线AB都是异面直线,直线A'C 与A'D'相对于直线AB的位置相同吗 如果不同,如何表示这种差异呢
一条直线相对于另一条直线的倾斜程度不同
用角度来表示这种差异
y
新知探究
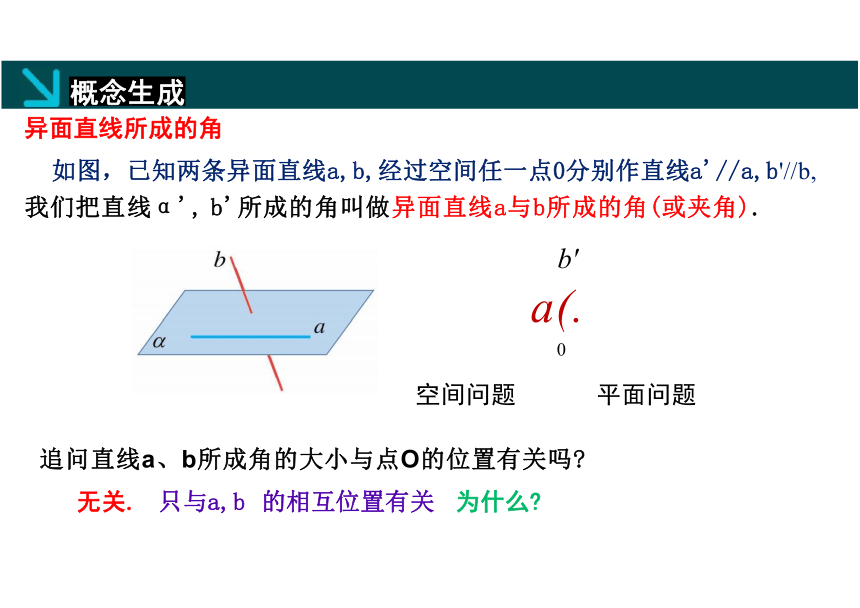
异面直线所成的角
如图,已知两条异面直线a,b,经过空间任一点0分别作直线a'//a,b'//b,
我们把直线α', b'所成的角叫做异面直线a与b所成的角(或夹角).
b'
a(.
0
空间问题 平面问题
追问直线a、b所成角的大小与点O的位置有关吗
无关. 只与a,b 的相互位置有关 为什么
概念生成
b
a
a
a
规 定 如果两条直线平行或重合,它们的夹角为0.
两条异面直线所成的角θ的取值范围:
空间两条直线所成的角θ的取值范围:
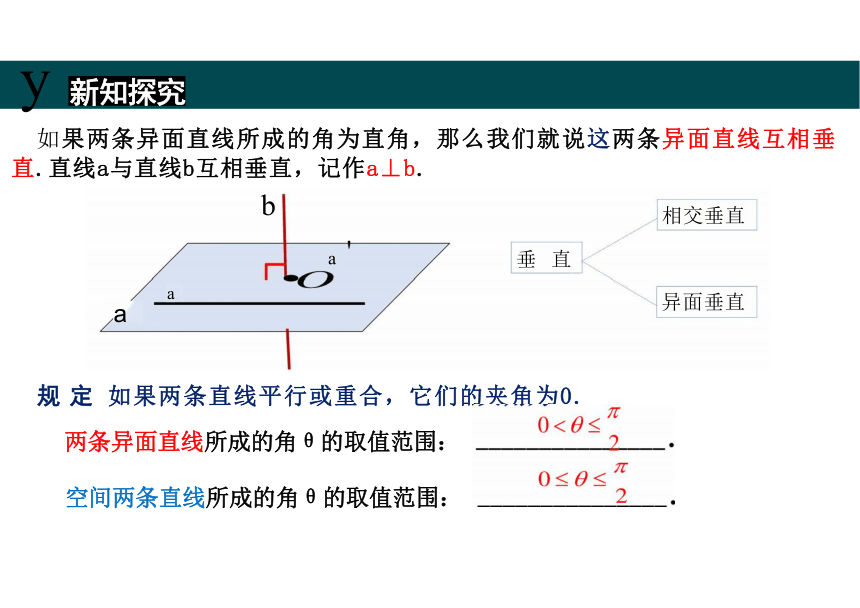
如果两条异面直线所成的角为直角,那么我们就说这两条异面直线互相垂 直.直线a与直线b互相垂直,记作a⊥b.
y
新知探究
异面垂直
相交垂直
垂 直
C'
2.如图,在长方体ABCD-A'B'C'D '的各条棱所在直线中, (1)与直线AB垂直的直线有_ 8 _ 条; (2)与直线AB异面且垂直的直线有 4 条; (3)与直线AB和A'D'都垂直的直线有 4 条;
1.判断下列命题是否正确,正确的在括号内画“ √ ”,错误的画“×”.
(1)如果两条平行直线中的一条与已知直线垂直,那么另一条也与已知直 线垂直. ( √ )
(2)垂直于同一条直线的两条直线平行. ( ×)
y 学以致用 教材P148
(4)与直线AB 和A'D'都垂直且相交的直线是直线_AA' 。
y典例分析
例 1 如右图,已知正方体ABCD-A'B'C'D'.
(1)哪些棱所在的直线与直线AA '垂直
(2)求直线BA'与CC'所成角的大小。
(3)求直线BA '与AC 所成角的大小。
解 :(1)上底面有:A'B',A'D',B'C',C'D',
下底面有:AB,AD,BC,CD,
(2)在正方体ABCD-A'B'C'D'中,∵CC'//BB',
∴∠B'BA 为直线BA '与CC '所成的角.而∠B'BA=45°.
∴直线BA '与CC '所成角的大小为45°.
(3)连接A'C',BC'.∴∠BA'C '为直线BA'与AC所成的角.
在正方体ABCD-A'B'C'D'中,△A'BC'是等边三角形,
∴∠BA'C'=60°, ∴直线BA '与AC 所成的角等于60°.
变式长方体ABCD-A B C D 中,AB=AA =2cm,
AD=1cm, 求异面直线A C 与BD 所成的角的余弦值 .
解法一 (平移法):
∠AOM (或补角)是直线A C 与 BD 所成的角
解法二(补形法): 5
∠A C E (或补角)是直线A C 与BD 所成的角
∴直线A C 与BD 所成的角的余弦值为
∴直线A C 与BD 所成的角的余弦值为
y 新知探究
√5
5
√5
求两条异面直线所成的角的一般步骤:
1. 作:恰当地选择一个点 (经常在其中一条线上取一点) , 作 出 ( 常 用 平移法)异面直线所成的角(或其补角);
2. 证:证明(1)中所作出的角(或其补角)就是所求异面直线所成的角; (注:证明线线平行)
3. 求: 通过解三角形或其他方法,求出(1)中所构造的角的大小;
(注:假如所构造的角的大小为a, 若0°V 方法归纳
(1)直线BC 和A'C'所成的角的大小;
(2)直线AA'和BC'所成的角的大小。
解 :(1)在长方体ABCD-A'B'C'D '中,∵BC//B'C',
∴∠B'C'A '为直线BC 与A'C'所成的角.
在Rt△A'B'C '中,A'B'=B'C',∴∠B'C'A'=45° .
∴直线BC与A'C'所成的角的大小为45°.
(2)∵AA'//BB',∴∠B'BC '为直线AA '与BC '所成的角.
在Rt△B'BC 中, BB'=2,B'C'=2√3,
∴tan ∠B'BC'=√3, ∴∠B'BC'=60°,
∴直线AA '与BC '所成的角的大小为60°.
C'
A
3. 如图,在长方体ABCD-A'B'C'D ' 中 ,AB=AD=2√3,AA'=2, 求:
学以致用 教材P148
例2 如右图,在正方体ABCD-A B C D 中 ,O 为底面A B C D 的中心,求 证 :AO ⊥BD.
证明:如图示,连接B D .
∵ABCD-A B C D 是正方体,∴BB //DD .
∴四边形BB D D 是平行四边形. ∴ B D I/BD.
∴直线AO 与B D 所成的角即为AO 与BD所成的角.
连接AB ,AD , 易 证AB =AD .
又 0 为 底 面 A B C D 的 中 心 ,
∴O 是 B D 的 中 点 ,
∴AO ⊥B D ,
∴AO ⊥BD.
典例分析
DE"BFo BDEF
BD//EF。又AB■BB2
AF■√5。AE■√2.EF●BD■√3.
AEF粤AE +EF ■AF ,&LAEF■90 °.
EFLACSZEF//BD BDLAC.
求证:BD⊥AC.
证明:如图示,取AC'的中点E, 连接DE, 取 B'B的中点F, 连接AF,EF.
A
学以致用 教材P148
4. 如图,在正三棱柱ABC-A'B'C'中,D 为棱AC的中点,AB=BB'=2.
追问你还能想出 其他解法吗
题型一 异面直线所成的角
例题 1. 在正方体ABCD-A B C D 中 ,E 为CC 的中点,求异面直B E与C D所
成角的余弦值.
则 ∠AB E(或其补角)为异面直线B E与C D所成的角, 设正方体的棱长为2,则 AB =2 √2 ,AE=3,B E =√5,
即异面直线B E与C D所成角的余弦值为
y 能力提升
[解析] 连接AE,B A, 在正方体ABCD-A B C D
所以四边形 AB C D 为平行四边形,
所以 B A//C D,
由余弦定理的推论得 cos∠
中 ,
①直接平移法(利用图中已有的平行线);
②中位线平移法(或线段成比例平移);
③补形平移法(在已知图形中,补成熟悉的几何体,以便找到平行线);
④平行四边形平移法(由一组对边平行且相等,从而得另一组对边平行).
注意:
若求出的角是锐角或直角,则它是所要求的异面直线所成的角;若求出 的角是钝角,则它的补角才是所要求的异面直线所成的角.
y 能力提升
作异面直线所成的角(或其补角)的四种方法.
方法总结
A. 30° B. 45° C. 60° D. 90°
[解析] 如图,取B C 的中点E, 连接BE,DE, 则DE//A C .
因为AC//A C ,
所以AC//DE,
所以∠BDE(或其补角)即为异面直线BD与AC所成的角.
由已知可得
BD=DE=BE= √2, 所以∠BDE=60°,
所以异面直线BD与AC所成的角为60° .
故选C
y
练习 1. 如图,在直三棱柱ABC-A B C 中 ,D为A B 的中点,AB=BC=2,B
B =1,AC=2√2, 则异面直线BD与AC所成的角为( 0
异面直线所成的角
能力提升
题型一
∵E,G 分别是 BD ,CD 的中点,
∴EG//BC,
∵F 是 AD 的中点,且
DF/BC,
∴ 四边形 EFDG 是平行四边形,∴ EF//DG,
直线与直线垂直
2. 如图,在长方体ABCD-A B C D 中 ,A A=AB,E,F 的中点.求证:CD ⊥EF.
∴∠DGD (或其补角)是异面直线 CD 与 EF 所成的角.
又 A A=AB, ∴ 四边形 ABB A 和四边形CDD C 都是正方形, ∴DG⊥CD ,∴CD ⊥EF.
y
证明 如图,取 CD 的中点 G, 连接 EG ,DG.
题型二
例题
能力提升
分别是BD ,AD
(1)定义:夹角为90° ;
(2)等腰三角形三线合一;
(3)菱形的对角线,直角梯形(直角腰与上下底都垂直),矩形的邻边;
(4)勾股定理的逆定理(最大边所对的角是直角);
(5)直径所对的圆周角是直角.
y 能力提升
证明线线垂直的常用方法
方法总结
题型二 直线与直线垂直
练习 2. 如图,在正方体ABCD-A B C D
求 证 :A0⊥A B.
证明 ∵ ABCD-A B C D 是正方体,
∴A D 兰BC,
∴四边形 A D CB 是平行四边形, ∴A B//D C,
∴直线 A0 与 A B 所成的角即为直线 AO 与 D C 所成的角, 连接AC,AD ( 图 略 ) ,
∵AC=AD ,0 为CD 的中点,
∴AO⊥D C,
∴AO⊥A B.
y 能力提升
中 ,CD 与DC 相交于点0,
异面直线
互相垂直
数学直观
数学运算 逻辑推理
将空间问题转化为平面问题的转化思想
y 课堂小结
异面直线 所成的角
相交直线 所成的角
类比
转化
范 围
步 骤
定 义
特殊
人教A 版2019必修第二册
感谢聆听
主 讲 :
第八章立体几何初步
人教A版2019必修第二册
8.6.1 直线与直线垂直
理解异面直线所成角的定义,并能做出异面直线的角
理解两条直线垂直的定义
通过实例,解决直线与直线平行的相关问题
学习目标
1
在同一平面内,有且只有一个公共点 .
共面直线
在同一平面内,没有公共点 .
异面直线 不同在任何一个平面内,没 有公共点 .
b β \b
b
a
α
在初中我们已经研究了平行直线和相交直线.本节我们主要研究异面 直线,首先研究如何刻画两条异面直线的位置关系.
空间两条直线的位置关系
相交直线
平行直线
y 复习回顾
a
图中的角θ即为直线a与直线b的夹角.
范围:[0,
规定:如果两条直线平行或重合,它们的夹角为0.
追问空间中两条直线所成角又该如何定义 它的范围又是多少
问题1平面中,两条相交直线形成几个角 两直线夹角的取值范围是多少
平面内两条直线相交形成4个角,其中不大于90°的角称为这两条直线
所成的角(或夹角) ,它刻画了一条直线相对于另一条直线倾斜的程度.
y 新知探究
问题2 如图示,在正方体ABCD-A'B'C'D '中,直线A'C 与直线AB, 直线A'D'
与直线AB都是异面直线,直线A'C 与A'D'相对于直线AB的位置相同吗 如果不同,如何表示这种差异呢
一条直线相对于另一条直线的倾斜程度不同
用角度来表示这种差异
y
新知探究
异面直线所成的角
如图,已知两条异面直线a,b,经过空间任一点0分别作直线a'//a,b'//b,
我们把直线α', b'所成的角叫做异面直线a与b所成的角(或夹角).
b'
a(.
0
空间问题 平面问题
追问直线a、b所成角的大小与点O的位置有关吗
无关. 只与a,b 的相互位置有关 为什么
概念生成
b
a
a
a
规 定 如果两条直线平行或重合,它们的夹角为0.
两条异面直线所成的角θ的取值范围:
空间两条直线所成的角θ的取值范围:
如果两条异面直线所成的角为直角,那么我们就说这两条异面直线互相垂 直.直线a与直线b互相垂直,记作a⊥b.
y
新知探究
异面垂直
相交垂直
垂 直
C'
2.如图,在长方体ABCD-A'B'C'D '的各条棱所在直线中, (1)与直线AB垂直的直线有_ 8 _ 条; (2)与直线AB异面且垂直的直线有 4 条; (3)与直线AB和A'D'都垂直的直线有 4 条;
1.判断下列命题是否正确,正确的在括号内画“ √ ”,错误的画“×”.
(1)如果两条平行直线中的一条与已知直线垂直,那么另一条也与已知直 线垂直. ( √ )
(2)垂直于同一条直线的两条直线平行. ( ×)
y 学以致用 教材P148
(4)与直线AB 和A'D'都垂直且相交的直线是直线_AA' 。
y典例分析
例 1 如右图,已知正方体ABCD-A'B'C'D'.
(1)哪些棱所在的直线与直线AA '垂直
(2)求直线BA'与CC'所成角的大小。
(3)求直线BA '与AC 所成角的大小。
解 :(1)上底面有:A'B',A'D',B'C',C'D',
下底面有:AB,AD,BC,CD,
(2)在正方体ABCD-A'B'C'D'中,∵CC'//BB',
∴∠B'BA 为直线BA '与CC '所成的角.而∠B'BA=45°.
∴直线BA '与CC '所成角的大小为45°.
(3)连接A'C',BC'.∴∠BA'C '为直线BA'与AC所成的角.
在正方体ABCD-A'B'C'D'中,△A'BC'是等边三角形,
∴∠BA'C'=60°, ∴直线BA '与AC 所成的角等于60°.
变式长方体ABCD-A B C D 中,AB=AA =2cm,
AD=1cm, 求异面直线A C 与BD 所成的角的余弦值 .
解法一 (平移法):
∠AOM (或补角)是直线A C 与 BD 所成的角
解法二(补形法): 5
∠A C E (或补角)是直线A C 与BD 所成的角
∴直线A C 与BD 所成的角的余弦值为
∴直线A C 与BD 所成的角的余弦值为
y 新知探究
√5
5
√5
求两条异面直线所成的角的一般步骤:
1. 作:恰当地选择一个点 (经常在其中一条线上取一点) , 作 出 ( 常 用 平移法)异面直线所成的角(或其补角);
2. 证:证明(1)中所作出的角(或其补角)就是所求异面直线所成的角; (注:证明线线平行)
3. 求: 通过解三角形或其他方法,求出(1)中所构造的角的大小;
(注:假如所构造的角的大小为a, 若0°
(1)直线BC 和A'C'所成的角的大小;
(2)直线AA'和BC'所成的角的大小。
解 :(1)在长方体ABCD-A'B'C'D '中,∵BC//B'C',
∴∠B'C'A '为直线BC 与A'C'所成的角.
在Rt△A'B'C '中,A'B'=B'C',∴∠B'C'A'=45° .
∴直线BC与A'C'所成的角的大小为45°.
(2)∵AA'//BB',∴∠B'BC '为直线AA '与BC '所成的角.
在Rt△B'BC 中, BB'=2,B'C'=2√3,
∴tan ∠B'BC'=√3, ∴∠B'BC'=60°,
∴直线AA '与BC '所成的角的大小为60°.
C'
A
3. 如图,在长方体ABCD-A'B'C'D ' 中 ,AB=AD=2√3,AA'=2, 求:
学以致用 教材P148
例2 如右图,在正方体ABCD-A B C D 中 ,O 为底面A B C D 的中心,求 证 :AO ⊥BD.
证明:如图示,连接B D .
∵ABCD-A B C D 是正方体,∴BB //DD .
∴四边形BB D D 是平行四边形. ∴ B D I/BD.
∴直线AO 与B D 所成的角即为AO 与BD所成的角.
连接AB ,AD , 易 证AB =AD .
又 0 为 底 面 A B C D 的 中 心 ,
∴O 是 B D 的 中 点 ,
∴AO ⊥B D ,
∴AO ⊥BD.
典例分析
DE"BFo BDEF
BD//EF。又AB■BB2
AF■√5。AE■√2.EF●BD■√3.
AEF粤AE +EF ■AF ,&LAEF■90 °.
EFLACSZEF//BD BDLAC.
求证:BD⊥AC.
证明:如图示,取AC'的中点E, 连接DE, 取 B'B的中点F, 连接AF,EF.
A
学以致用 教材P148
4. 如图,在正三棱柱ABC-A'B'C'中,D 为棱AC的中点,AB=BB'=2.
追问你还能想出 其他解法吗
题型一 异面直线所成的角
例题 1. 在正方体ABCD-A B C D 中 ,E 为CC 的中点,求异面直B E与C D所
成角的余弦值.
则 ∠AB E(或其补角)为异面直线B E与C D所成的角, 设正方体的棱长为2,则 AB =2 √2 ,AE=3,B E =√5,
即异面直线B E与C D所成角的余弦值为
y 能力提升
[解析] 连接AE,B A, 在正方体ABCD-A B C D
所以四边形 AB C D 为平行四边形,
所以 B A//C D,
由余弦定理的推论得 cos∠
中 ,
①直接平移法(利用图中已有的平行线);
②中位线平移法(或线段成比例平移);
③补形平移法(在已知图形中,补成熟悉的几何体,以便找到平行线);
④平行四边形平移法(由一组对边平行且相等,从而得另一组对边平行).
注意:
若求出的角是锐角或直角,则它是所要求的异面直线所成的角;若求出 的角是钝角,则它的补角才是所要求的异面直线所成的角.
y 能力提升
作异面直线所成的角(或其补角)的四种方法.
方法总结
A. 30° B. 45° C. 60° D. 90°
[解析] 如图,取B C 的中点E, 连接BE,DE, 则DE//A C .
因为AC//A C ,
所以AC//DE,
所以∠BDE(或其补角)即为异面直线BD与AC所成的角.
由已知可得
BD=DE=BE= √2, 所以∠BDE=60°,
所以异面直线BD与AC所成的角为60° .
故选C
y
练习 1. 如图,在直三棱柱ABC-A B C 中 ,D为A B 的中点,AB=BC=2,B
B =1,AC=2√2, 则异面直线BD与AC所成的角为( 0
异面直线所成的角
能力提升
题型一
∵E,G 分别是 BD ,CD 的中点,
∴EG//BC,
∵F 是 AD 的中点,且
DF/BC,
∴ 四边形 EFDG 是平行四边形,∴ EF//DG,
直线与直线垂直
2. 如图,在长方体ABCD-A B C D 中 ,A A=AB,E,F 的中点.求证:CD ⊥EF.
∴∠DGD (或其补角)是异面直线 CD 与 EF 所成的角.
又 A A=AB, ∴ 四边形 ABB A 和四边形CDD C 都是正方形, ∴DG⊥CD ,∴CD ⊥EF.
y
证明 如图,取 CD 的中点 G, 连接 EG ,DG.
题型二
例题
能力提升
分别是BD ,AD
(1)定义:夹角为90° ;
(2)等腰三角形三线合一;
(3)菱形的对角线,直角梯形(直角腰与上下底都垂直),矩形的邻边;
(4)勾股定理的逆定理(最大边所对的角是直角);
(5)直径所对的圆周角是直角.
y 能力提升
证明线线垂直的常用方法
方法总结
题型二 直线与直线垂直
练习 2. 如图,在正方体ABCD-A B C D
求 证 :A0⊥A B.
证明 ∵ ABCD-A B C D 是正方体,
∴A D 兰BC,
∴四边形 A D CB 是平行四边形, ∴A B//D C,
∴直线 A0 与 A B 所成的角即为直线 AO 与 D C 所成的角, 连接AC,AD ( 图 略 ) ,
∵AC=AD ,0 为CD 的中点,
∴AO⊥D C,
∴AO⊥A B.
y 能力提升
中 ,CD 与DC 相交于点0,
异面直线
互相垂直
数学直观
数学运算 逻辑推理
将空间问题转化为平面问题的转化思想
y 课堂小结
异面直线 所成的角
相交直线 所成的角
类比
转化
范 围
步 骤
定 义
特殊
人教A 版2019必修第二册
感谢聆听
主 讲 :
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
