--人教版八年级数学下册18.2.3 正方形小节复习题(含详解)
文档属性
| 名称 | --人教版八年级数学下册18.2.3 正方形小节复习题(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-22 14:21:49 | ||
图片预览




文档简介
18.2.3 正方形小节复习题
【题型1 正方形与矩形、菱形的性质的区别与练习】
1.学习了四边形之后,小颖同学用如下图所示的方式表示了四边形与特殊四边形的关系,则图中的“M”和“N”分别表示( )
平行四边形,正方形 B.正方形,菱形
C.正方形,矩形 D.矩形,菱形
2.下列性质中,矩形、正方形都具有,但是菱形却不具有的性质是( )
A.对角线长度相等 B.对角线互相垂直
C.对角线互相平分 D.一组对角线平分一组对角
3.用两块完全重合的等腰直角三角形纸片拼下列图形:(1)平行四边形(不包含菱形、矩形、正方形);(2)矩形;(3)正方形;(4)等边三角形;(5)等腰直角三角形,一定能拼成的图形是( )
A.(1)(2)(3) B.(1)(3)(5)
C.(2)(3)(5) D.(1)(3)(4)(5)
4.如图,在平行四边形中,E、F是对角线上的两点(不与点A、C重合),且,分别连接,则下列结论错误的是( )
A.四边形是平行四边形
B.若四边形是菱形,那么四边形也是菱形
C.若四边形是正方形,那么四边形是菱形
D.若四边形是矩形,那么四边形也是矩形
【题型2 由正方形的性质求角度】
1.如图,在正方形中,点、分别为边、上的点,连接、,平分,若.当时,则的度数为( )
A. B.
C. D.
2.如图,正方形中,点分别在上,,经过对角线的中点O,若,则一定等于( )
A. B. C. D.
3.如图,在正方形中,点在对角线上,且;延长交于点,连接,则的度数为 .
4.如图,正方形的对角线与交于点,点为边上一点,连接,过点作于点,连接,若,则的度数为( )
A. B. C. D.
【题型3 由正方形的性质求线段长】
1.如图,在边长为4的正方形中,点是上一点,点是延长线上一点,连接,,平分.交于点.若,则的长度为( )
A.2 B. C. D.
2.如图,将正方形放在平面直角坐标系中,是原点,的坐标为则点的坐标为 ( )
A. B.
C. D.
3.如图,正方形和正方形中,点在上,,,于点,那么的长是( )
A. B. C. D.
4.如图,在边长为6的正方形中,点E,F分别是边上的动点,且满足,与交于点O,点M是的中点,G是边上的点,,则的最小值是( )
A.4 B.5 C.8 D.10
【题型4 由正方形的性质求面积】
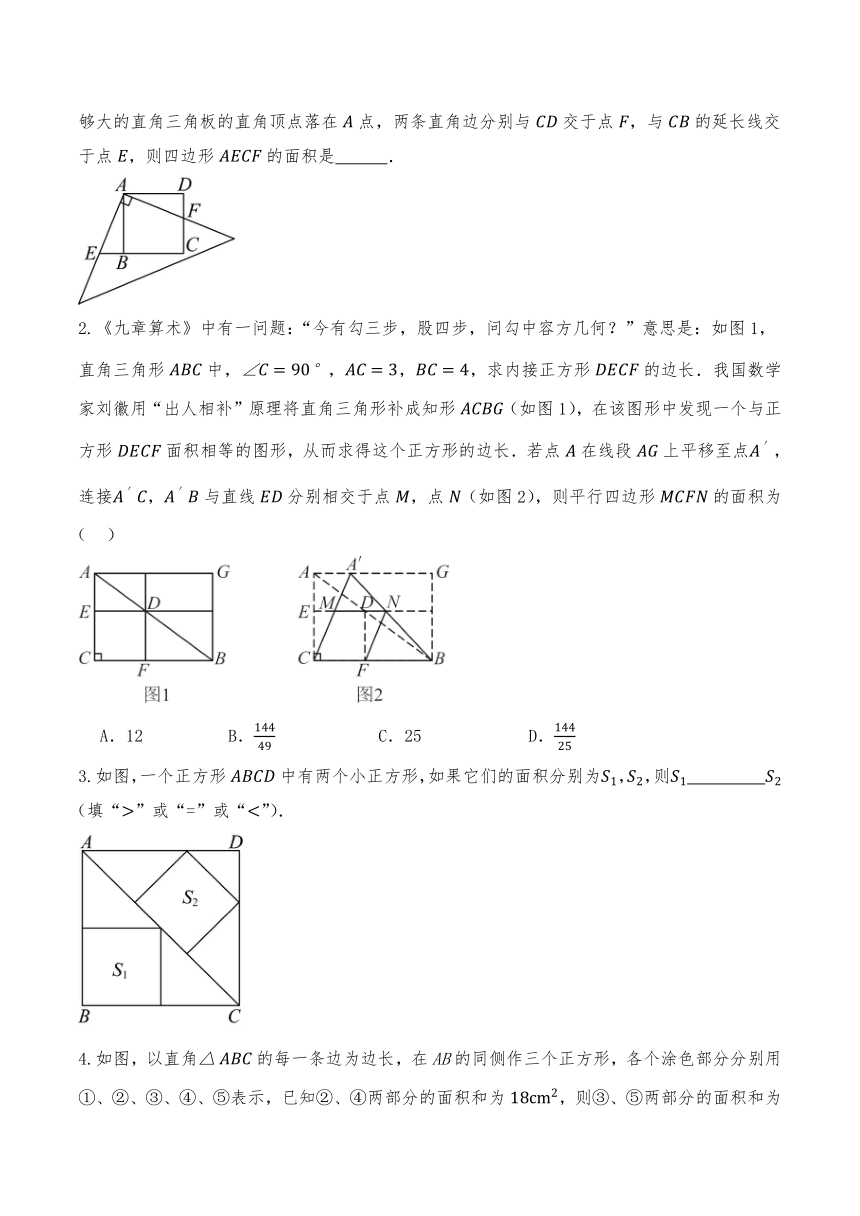
1.如图,有一块边长为4的正方形(四条边相等,四个角是直角)塑料模板,将一块足够大的直角三角板的直角顶点落在点,两条直角边分别与交于点,与的延长线交于点,则四边形的面积是 .
2.《九章算术》中有一问题:“今有勾三步,股四步,问勾中容方几何?”意思是:如图1,直角三角形中,,,,求内接正方形的边长.我国数学家刘徽用“出人相补”原理将直角三角形补成知形(如图1),在该图形中发现一个与正方形面积相等的图形,从而求得这个正方形的边长.若点在线段上平移至点,连接,与直线分别相交于点,点(如图2),则平行四边形的面积为( )
A.12 B. C.25 D.
3.如图,一个正方形中有两个小正方形,如果它们的面积分别为,,则 (填“”或“=”或“”).
4.如图,以直角的每一条边为边长,在AB的同侧作三个正方形,各个涂色部分分别用①、②、③、④、⑤表示,已知②、④两部分的面积和为,则③、⑤两部分的面积和为( ).
A.8 B.9 C.10 D.11
【题型5 正方形中的折叠问题】
1.如图,正方形纸片的边长为12,是边上一点,连接,点在上,沿折叠,使点落在上的点,若,则的长为 .
2.如图,将边长为8的正方形纸片沿对折再展平,沿折痕剪开,得到矩形和矩形,再将矩形绕点顺时针方向旋转.使点与点重合,点的对应点为,则图②中阴影部分的周长为( )
A.9 B.10 C.16 D.20
3.如图,在正方形中,,点E,F分别在边上,.若将四边形沿折叠,点B恰好落在边上,则的长度为( )
A.1 B. C. D.2
4.如图,取一张矩形的纸片进行折叠,具体操作过程如下:
(1)【课本再现】
第一步:如图1,对折矩形纸片,使与重合,折痕为,把纸片展平;
第二步:在上选一点P,沿折叠纸片,使点A落在矩形内部的点M处,连接,根据以上操作,当点M在上时,___________;
(2)【类比应用】
如图2,现将矩形纸片换成正方形纸片,继续探究,过程如下:将正方形纸片按照(1)中的方式操作,并延长交于点Q,连接,当点M在上时,求的度数;
(3)【拓展延伸】
在(2)的探究中,正方形纸片的边长为,改变点P在上的位置(点P不与点A,D重合),沿折叠纸片,使点A落在矩形内部的点M处,连接,并延长交于点Q,连接.当时,请求出的长.
【题型6 正方形中的证明】
1.如图,在正方形纸片中,P为正方形边上的一点(不与点A,D重合),将正方形纸片折叠,使点B落在点P处,点C落在点G处,交于点H,折痕为,连接,,交于点M,连接.
(1)求证:平分;
(2)求证:;
(3)探究,与的数量关系,并说明理由.
2.已知;正方形的边长是4,F是边的中点,E是上的点,且,如图,求证:.
3.正方形的边长为6,正方形的顶点E、F分别在正方形的对角线和边上,,连接.
(1)求证:;
(2)求的值.
4.【阅读材料】
在学习正方形时,我们遇到过这样的问题:如图1,在正方形中,点E、F、G、H分别在、、、上,且,垂足为M,那么与相等吗?
分别过点G、H作、,垂足分别为P、Q,通过证明,得到.
根据阅读材料,完成下面探究1、探究2中的问题.
【探究1】
如图2,在正方形中,点E在上,使用无刻度的直尺和圆规作,交于点F(要求直尺、圆规各使用一次),保留作图痕迹,并标出点F,不要求写作法;
【探究2】
如图3,在正方形中,点E、F分别在、上,将正方形沿着翻折,点B、C分别落在、处,且经过点D,将纸片展开,延长交于点G,连接交于点M.
(1)求证:;
(2)求证:.
【题型7 正方形与矩形、菱形的判定定理的区别】
1.甲,乙两位同学采用折叠的方法,判断两张四边形纸片是否为正方形.
甲:如图①进行两次折叠,每次折叠后折痕两侧部分能完全重合,故判断原四边形是正方形;
乙:如图②进行两次折叠,每次折叠后折痕两侧部分能完全重合,故判断原四边形是正方形.
下列判断正确的是( )
A.仅甲正确 B.仅乙正确 C.甲、乙均正确 D.甲、乙均错误
2.下列命题:
①对角线相等的菱形是正方形;
②对角线互相垂直平分且相等的四边形是正方形;
③对角线互相垂直且相等的平行四边形是正方形;
④对角线互相垂直的矩形是正方形;
其中是真命题的个数是( )
A.个 B.个 C.个 D.个
3.如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边上的中点,连结AC、BD,回答问题
(1)对角线AC、BD满足条件 时,四边形EFGH是矩形.
(2)对角线AC、BD满足条件 时,四边形EFGH是菱形.
(3)对角线AC、BD满足条件 时,四边形EFGH是正方形.
4.如图,已知四边形是平行四边形,下列结论中不正确的是( )
A.当时,它是菱形 B.当时,它是菱形
C.当时,它是矩形 D.当时,它是正方形
【题型8 证明四边形是正方形】
1.如图1,四边形为正方形,为对角线上一点,连接,.
(1)求证:;
(2)如图2,过点作,交边于点,以,为邻边作矩形,连接.
求证:矩形是正方形;
若正方形的边长为,,求正方形的边长.
2.如图,在矩形中,是边上一点,是的延长线上一点,连接,,已知,.
(1)求证:四边形是正方形.
(2)若,,求四边形的面积.
3.问题情境:数学活动课上,同学们开展了以“矩形纸片折叠”为主题的探究活动(每个小组的矩形纸片规格相同),已知矩形纸片宽.
(1)如图1,小组将矩形纸片折叠,点落在边上的点处,折痕为,连接,然后将纸片展平,得到四边形.求证:四边形是正方形;
(2)如图2,小组将矩形纸片对折使与重合,展平后得到折痕,再次过点折叠使点落在折痕上的点处,得到折痕,连结,展平后得到四边形,求四边形的面积;
4.综合与实践
问题解决:
(1)如图1,在中,是边上的中线,是的中点,过点作,交的延长线于点,连接.求证:四边形是平行四边形.
类比迁移:
(2)如图2,在(1)的条件下,当时,试判断四边形的形状,并说明理由.
拓展应用:
(3)当满足什么条件时,四边形是正方形?请直接写出结论,不必证明.
【题型9 由正方形性质与判定求线段长度】
1.正方形工整、匀称、美观,设计方便,在人们的生活和生产实际中有着广泛的应用.如图1为某园林石窗,其外框为边长为6的正方形(如图2),点E,F,G,H分别为边上的中点,以四边形各边的三等分点的连线为边,分别向内作等边三角形(如),四个等边三角形的顶点恰好是正方形MNPQ各边的中点,则点H,M之间的距离是 .
2.如图,在四边形中,,,,,则对角线的长为 .
3.综合与实践
问题情境:“综合与实践”课上,老师提出如下问题:如图1,在中,,点O是边的中点,连接.保持不动,将从图1的位置开始,绕点O顺时针旋转得到,点A,D,C的对应点分别为点E,F,G.当线段与线段相交于点M(点M不与点A,B,F,G重合)时,连接.老师要求各个小组结合所学的图形变换的知识展开数学探究.
(1)初步思考:如图2,连接,“勤学”小组在旋转的过程中发现,请你证明这一结论;
(2)操作探究:如图3,连接,“善思”小组在旋转的过程中发现垂直平分,请你证明这一结论;
(3)拓展延伸:已知,,在旋转的过程中,当以点F,C,D为顶点的三角形是等腰三角形时,请直接写出此时线段的长度.
4.如图,已知四边形是正方形,,点E为对角线上一动点,连接,过点E作,交射线于点F,以,为邻边作矩形,连,的最小值为 .
【题型10 由正方形性质与判定求角度】
1.四边形 ABCD 为正方形,点 E 为线段 AC 上一点,连接 DE,过点 E 作 EF ⊥DE,交射线 BC 于点 F,以 DE、EF 为邻边作矩形 DEFG,连接 CG.
(1)如图,求证:矩形 DEFG 是正方形;
(2)若 AB=,CE=2,求 CG 的长;
(3)当线段 DE 与正方形 ABCD 的某条边的夹角是 40°时,直接写出∠EFC 的度数.
2.已知:是的角平分线,点在边上,,过点作,交于点,连接.
(1)如图1,求证:四边形是菱形;
(2)如图2,当时,在不添加任何辅助线的情况下,请直接写出图2中度数为的度数2倍的角.
3.如图,用四个完全相同的矩形拼成了一个大正方形,AB是其中一个小矩形的对角线,请在大正方形中完成下列画图,要求:①仅用无刻度的直尺;②保留必要的画图痕迹.
(1)在图中画出一个以AB为边的正方形;
(2)在图中画出一个以点A或点B为顶点,AB为一边的45°角,并说明理由.
4.如图,在中,,将绕点C顺时针旋转得到,点B的对应点为E,点A的对应点D落在线段上,与相交于点F,连接.
(1)求证:平分;
(2)试判断与的位置关系,并说明理由;
(3)若,求的大小.(直接写出结果即可)
【题型11 由正方形性质与判定求面积】
1.【问题一】如图①,正方形的对角线相交于点O,点O又是正方形的一个顶点, 交于点E, 交于点F,则与的数量关系为______;
【问题二】受图①启发,兴趣小组画出了图②:直线m、n经过正方形的对称中心O,直线m分别与交于点E、F,直线n分别与交于点G、H,且 ,若正方形边长为8,求四边形的面积;
【问题三】在图②中,连接E、G、F、H四点,请证明四边形是正方形.
2.如图,阴影部分是一个正方形广场,规划将正方形的四边各延长一倍,即、、、,将M、N、P、Q四点连接,建成新的广场,试问建成的新广场是什么形状,并且它的面积是原广场的多少倍?
3.已知,如图,在四边形中,,,,垂足为点E.
(1)求证:;
(2)若,,求四边形的面积.
4.我们知道:有一个角是直角的三角形叫做直角三角形.类似地,我们定义:至少有一组对角是直角的四边形叫做对角直角四边形.
(1)下列图形:①有一个内角为的平行四边形;②矩形;③菱形;
④直角梯形,其中对角直角四边形是 (只填序号);
(2)如图,菱形的对角线,相交于点,在菱形的外部以为斜边作等腰直角,连接.
①求证:四边形是对角直角四边形;
②若点到的距离是2,求四边形的面积.
【题型12 由正方形性质与判定证明】
1.如图①,在正方形中,点分别在上且.
(1)试探索线段的大小关系,写出你的结论并说明理由;
(2)连接,分别取的中点,顺次连接,得到四边形:
①请在图②中补全图形;
②四边形是什么特殊平行四边形?请说明理由.
2.如图,若点是正方形外一点,且,,,则 °.
3.如图,E,F,M,N分别是正方形四条边上的点,且.试判断四边形是什么图形,并证明你的结论.
4.问题情境:通过对《平行四边形》一章内容的学习,我们认识到矩形、菱形、正方形都是特殊的平行四边形,它们除了具有平行四边形的性质外,还有各自的特殊性质.根据它们的特殊性,得到了这些特殊的平行四边形的判定定理.数学课上,老师给出了一道题:如图①,矩形的对角线,交于点O,过点D作,且,连接.
初步探究:
(1)判断四边形的形状,并说明理由.
深入探究:
(2)如图②,若四边形是菱形,(1)中的结论还成立吗?请说明理由.
拓展延伸:
(3)如图③,若四边形是正方形,四边形又是什么特殊的四边形?请说明理由.
参考答案
【题型1 正方形与矩形、菱形的性质的区别与练习】
1.B
【分析】本题考查了特殊的平行四边形,正确理解矩形,菱形,正方形之间的关系是解题的关键.
根据特殊的平行四边形的概念判断即可.
【详解】解:∵矩形和菱形是特殊的平行四边形,正方形即是菱形也是矩形,
∴是正方形,是菱形,
故选:B
2.A
【分析】利用正方形的性质,矩形的性质,菱形的性质依次判断可求解.
【详解】解:菱形具有的性质是:两组对边分别平行,对角线互相平分,对角线互相垂直;
矩形具有的性质是:两组对边分别平行,对角线互相平分,对角线相等;
正方形具有菱形和矩形的性质,
故选项B,C,D不符合题意;
菱形不具有的性质为:对角线长度相等,
故选项A符合题意.
故选:A.
3.B
【分析】通过不同的组合方法,得出不同的图形.
【详解】解:用两块完全重合的等腰直角三角形纸片可以拼成下列图形:
(1)平行四边形
(3)正方形
(5)等腰直角三角
故选B.
4.D
【分析】本题考查了平行四边形的判定和性质,菱形的判定和性质,矩形的判定和性质, 正方形的性质,熟练掌握这些知识是解题的关键.连接交于点O,根据平行四边形的性质可得, 再根据E、F是对角线上的两点(不与点A、C重合),,可得,进一步即可判断A选项; 根据菱形的性质可得,进一步即可判断选项; 根据正方形的性质可得,进一步即可判断选项;根据矩形的性质可得, 再根据E、F是对角线上的两点 (不与点A、C重合),可得,进一步可判断选项.
【详解】解:连接交于点O,如图所示:
∵四边形是平行四边形,
∴,
∵E、F是对角线上的两点(不与点A、C重合), ,
∴,
∵,
∴四边形是平行四边形,故A不符合题意;
当四边形是菱形时, ,
∴,
又∵四边形是平行四边形,
∴四边形是菱形,
故不符合题意;
当四边形是正方形时, ,
∴,
又∵四边形是平行四边形,
∴四边形是菱形,
故不符合题意;
当四边形是矩形时, ,
∵E、F是对角线上的两点(不与点A、C重合),
∴,
∴四边形不是矩形,
故符合题意,
故选:.
【题型2 由正方形的性质求角度】
1.C
【分析】本题考查了正方形的性质,角平分线的定义,全等三角形的判定和性质,由正方形的性质可得,,,进而由可得,,再由角平分线的定义得,又证明可得,最后利用角的和差关系即可求解,掌握正方形的性质是解题的关键.
【详解】解:∵四边形是正方形,
∴,,
∵,
∴,
∴,
∵平分,
∴,
在和中,
,
∴,
∴,
∴,
故选:.
2.B
【分析】证明,可得,利用直角三角形斜边上的中线等于斜边的一半,可得,则可得,利用三角形外角和定理,即可得到的值.
【详解】解:四边形是正方形,
,
经过对角线的中点O,
,
在与中,
,
,
,
,
,
,
,
故选:B.
3.
【分析】根据正方形的性质可得,,再根据又证得,得,,根据三角形内角和定理求得,最后根据平角定义求得答案.
【详解】解:正方形,
,,
又,
,
,,
,
,
,
故答案为:.
4.C
【分析】本题主要考查了正方形的性质,直角三角形斜边上的中线等于斜边的一半,等边对等角以及三角形外角性质等知识,取中点G,连接,,设与交于点,证明,得,证明,求出,根据可得,整理后可得结论
【详解】解:取中点G,连接,,设与交于点,如图,
∵四边形是正方形,
∴,,
∴,,
又,
∴
∴
∴
∵,
∴,
∵
∴
在和中,
∴,
∵,且,
∴
∴
而
又
∴
∴.
故选:C.
【题型3 由正方形的性质求线段长】
1.D
【分析】本题主要考查了正方形的性质,全等三角形的性质与判定,勾股定理,先由正方形的性质得到,再证明得到,进一步证明得到,设,则,
在中,由勾股定理得,解方程即可得到答案.
【详解】解:∵四边形是正方形,
∴,
又∵,
∴,
∴,
∵平分,
∴,
又∵,
∴,
∴,
设,则,
在中,由勾股定理得,
∴,
解得,
∴,
故选:D.
2.D
【分析】过点作轴于,过点作的延长线于,交y轴于点,由可证,可得,,据此即可求解.
【详解】解:如图,过点作轴于,过点作的延长线于,交y轴于点,
点的坐标为,
,,
∵轴轴,
∴四边形是矩形,
∴
四边形是正方形,
,,
,,
,
,
,
在和中,
,
,
,,
,
点的坐标为,
故选:D.
3.D
【分析】本题考查了正方形的性质,勾股定理,直角三角形的面积,连接,由正方形的性质得到,,利用勾股定理可求得,,,再根据三角形的面积得到,代入已求计算即可求解,由正方形的性质得到是解题的关键.
【详解】解:连接,
∵正方形和正方形,
∴,,
∵,,
∴,,,
∴,
∵,
∴,
即,
解得,
故选:.
4.B
【分析】本题主要考查了正方形的性质,全等三角形的性质与判定,直角三角形的性质,勾股定理等等,先证明得到,进而得到,则由直角三角形的性质可得,如图所示,在延长线上截取,连接,易证明,则,可得当H、D、F三点共线时,有最小值,即此时有最小值,最小值即为的长的一半,求出,在中,由勾股定理得,责任的最小值为5.
【详解】解:∵四边形是正方形,
∴,
又∵,
∴,
∴,
∴,
∵点M是的中点,
∴;
如图所示,在延长线上截取,连接,
∵,
∴,
∴,
∴,
∴当H、D、F三点共线时,有最小值,即此时有最小值,最小值即为的长的一半,
∵,,
∴,
∴,
在中,由勾股定理得,
∴的最小值为5,
故选:B.
【题型4 由正方形的性质求面积】
1.16
【分析】证明,得到,计算即可.
【详解】∵正方形,
∴,,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
故答案为:16.
2.B
【分析】本题考查了正方形和矩形的性质,正确列出方程是解答本题的关键.设正方形的边长为x,证明,则,得到 解得,即可求出正方形的边长为,即可得到答案.
【详解】如图1,设正方形的边长为x,
根据题意得,四边形都是矩形,
∴
∴
∴
∵,,
∴
∴
解得,
∴正方形的边长为,
∴正方形的边长为,
∵平行四边形的面积
故选:B.
3.
【分析】本题考查了正方形的性质,勾股定理等等知识,设正方形的边长为6,然后求出与的值,问题得解.
【详解】解:如图,设正方形的边长为6,
∵是正方形的对角线,
,,
∴,
又∵四边形与四边形是正方形,
,,
,,
,,
∴.
故答案为:.
4.B
【分析】设序号为①,②,③,④,⑤图形的面积分别为,,,,,利用正方形性质,三角形全等证明即可,本题考查了正方形的性质,勾股定理,三角形全等的判定和性质,熟练掌握正方形的性质,勾股定理是解题的关键.
【详解】如图所示,
设序号为①,②,③,④,⑤图形的面积分别为,,,,,,
根据题意,得,
四边形是正方形,,
,
,,
,
,
.
∴
∵②、④两部分的面积和为,
∴,
四边形是正方形,四边形是正方形,
,
,
.
∴,
根据题意,得
,
故选B.
【题型5 正方形中的折叠问题】
1.
【分析】本题考查了正方形的性质,轴对称的性质 ,全等三角形的判定与性质,勾股定理,面积法求线段的长度等,解题关键是能够灵活运用正方形的性质和轴对称的性质.
由折叠及轴对称的性质可知, 垂直平分, 先证推出的长,再利用勾股定理求出的长, 最后在中利用面积法可求出的长,可进一步求出的长,的长.
【详解】解:设与交于点M,
在正方形中,
,
在中,,
∵由折叠的性质可得
,
∴垂直平分,
,
∵,
所以,
又∵,,
∴,
∴,
又∵,
故答案为:
2.D
【分析】本题主要考查全等三角形的判定与性质,勾股定理以及菱形的判定与性质等,解答本题的关键是勾股定理以及菱形的判定.首先根据已知条件判断出,得到,,然后可设的长度为x,则,根据勾股定理列方程可解出x,最后证明阴影部分是菱形后,即可求出其周长.
【详解】解:如图,设交于G,旋转后交于点H,
由题意知,,,
又∵,
∴,
∴,,
设,则,
在中,,
解得:,
∴,
∵,,
∴四边形为平行四边形,
又∵,
∴为菱形,
∴阴影部分的周长为:,
故选:D.
3.D
【分析】本题考查正方形的性质,折叠的性质,含30度角的直角三角形的性质,解题的关键是熟练运用以上性质;根据可得根据折叠后对应角相等、对应边相等,可得,进而可得,根据含30度角的直角三角形的性质可得,设,则,列方程求解即可.
【详解】解:四边形是正方形,
将四边形沿折叠,点B恰好落在边上,
,
,
设,则,
,
,
,
故选:D.
4.(1)解:如图,连接,
∵对折矩形纸片,使与重合,折痕为,
∴垂直平分,
∴,,
∵沿折叠纸片,使点落在矩形内部的点处,
∴,,
∴,
∴是等边三角形,
∴,
∴,
故答案为:;
(2)解:如图,
同(1)可证,
∴,
在正方形中,,,
由折叠知,,
∴,,
在和中,
,
∴,
∴,
∴
(3)解:当点Q在点F的下方时,如图,
∵正方形中,,
∴,
∴,
由(2)知,
∴,
设,由折叠知,
∴,,
在中,,
∴,
解得,即;
当点Q在点F的上方时,如图,
则,
∴,
∴,
设,
则,,
在中,,
∴,
解得,即;
综上可知,的长为或.
【题型6 正方形中的证明】
1.(1)证明:由题意,得,
∴.
∵四边形是正方形,
∴,
∴,即.
又∵,
∴,
∴,即平分.
(2)证明:如图1,过点F作于点K,设交于点O.
∵,
∴四边形是矩形,
∴.
∵点B与点P关于对称,
∴,
∴,
∴.
∵,
∴.
∵,
∴,
∴.
(3)解:.
理由:如图,过点B作,垂足为Q.
由(1)知,.
∵,
∴.
∵,
∴,
∴.
又∵,
∴.
∵,
∴,
∴,
∴,
即.
2.证明:连接,延长交延长线于点G,如图:
∵正方形,
,
,
,
∴设,则,
在中,,
∵点F是中点,
∴,
∵,
,
,
,
,
又∵
.
3.(1)证明:∵正方形和,
∴,,,
∴,
∴,
∴;
(2)解:连接和,
∵正方形的边长为6,且,
∴,,,
∴,
由(1)得,,
∴,
∴,
∴.
4.解∶[探究1]
如图,即为所求,
∵四边形是正方形,
∴,,,
由作图知:,
∴,
∴,
∵,
∴,
∴;
[探究2]
(1)证明:∵翻折,
∴,,
又,
∴,
∴;
(2)连接,过F作于N,
则四边形是矩形,
∴,,
又,
∴,
∵翻折,
∴,
∵,,
∴,,
又,
∴,
∴,
又,
∴,
∴,
∵,
∴,
∴,
又,,
∴,
∴,
又,,
∴
【题型7 正方形与矩形、菱形的判定定理的区别与练习】
1.D
【分析】利用折叠的性质和菱形、矩形、正方形的判定即可得出答案.
【详解】解∶①按照图①折叠,可得四边形的四边相等,原四边形是菱形或正方形;
②按照图②折叠,可得四边形的四个角相等,不能得四条边相等,原四边形是矩形;
故选∶ D.
2.A
【分析】利用正方形的判定方法分别判断后即可确定正确的选项.
【详解】解:对角线相等的菱形是正方形,正确,是真命题,符合题意;
对角线互相垂直平分且相等的四边形是正方形,正确,是真命题,符合题意;
对角线互相垂直且相等的平行四边形是正方形,正确,是真命题,符合题意;
对角线互相垂直的矩形是正方形,正确,是真命题,符合题意.
真命题有个,
故选A.
3. AC⊥BD AC=BD AC⊥BD且AC=BD
【分析】先证明四边形EFGH是平行四边形,
(1)在已证平行四边形的基础上,要使所得四边形是矩形,则需要一个角是直角,故对角线应满足互相垂直
(2)在已证平行四边形的基础上,要使所得四边形是菱形,则需要一组邻边相等,故对角线应满足相等
(3)联立(1)(2),要使所得四边形是正方形,则需要对角线垂直且相等
【详解】解:连接AC、BD.
∵E、F、G、H分别是AB、BC、CD、DA边上的中点,
∴EF∥AC,EF=AC,FG∥BD,FG=BD,GH∥AC,GH=AC,EH∥BD,EH=BD.
∴EF∥HG,EF=GH,FG∥EH,FG=EH.
∴四边形EFGH是平行四边形;
(1)要使四边形EFGH是矩形,则需EF⊥FG,
由(1)得,只需AC⊥BD;
(2)要使四边形EFGH是菱形,则需EF=FG,
由(1)得,只需AC=BD;
(3)要使四边形EFGH是正方形,综合(1)和(2),
则需AC⊥BD且AC=BD.
故答案是:AC⊥BD;AC=BD;AC⊥BD且AC=BD
4.D
【分析】此题主要考查学生对正方形的判定、平行四边形的性质、菱形的判定和矩形的判定的理解和掌握,此题涉及到的知识点较多,学生答题时容易出错.
根据邻边相等的平行四边形是菱形;根据所给条件可以证出邻边相等;根据有一个角是直角的平行四边形是矩形;根据对角线相等的平行四边形是矩形.
【详解】解:A、根据邻边相等的平行四边形是菱形可知:四边形是平行四边形,当时,它是菱形,故A选项正确,不符合题意;
B、四边形是平行四边形,,
四边形是菱形,故B选项正确,不符合题意;
C、有一个角是直角的平行四边形是矩形,故C选项正确,不符合题意;
D、根据对角线相等的平行四边形是矩形可知当时,它是矩形,不是正方形,故D选项错误,符合题意.
故选:D.
【题型8 证明四边形是正方形】
1.(1)证明:∵四边形为正方形,
∴,,
在和中,
,
∴,
∴;
(2)①证明:如图,作于,于,则四边形为矩形,
∴,
∵点是正方形对角线上的点,
∴,
∵,
∴,
∵,
在和中
∴,
∴,
∵四边形是矩形,
∴矩形是正方形;
②解:正方形和正方形中,,,
,
∴,
∴,
∴,,
∵,
∴,
∴,
∴,
∵,
∴,
连接,
∴,
∴,
即正方形的边长为.
2.(1)证明:四边形是矩形,
,
,.
,
,
,
,
,
.
矩形是正方形.
(2)解:,,
,
.
.
3.(1)四边形是正方形,理由如下:
∵四边形是矩形,
∴,,
∴,
由第一步折叠可知:,
∴,
∴,
∴,
∴四边形是菱形,
又∵,
∴四边形是正方形;
(2)连接,
由折叠得,
∴
∴
∴是等边三角形,
∴
∴
设则,
由勾股定理得,
∴
解得,(负值舍去)
∴
由折叠得,,
∴.
4.证明:(1),
,
是的中点,
,
在和中,
,
,
,
是边上的中线,
,
,
又,
四边形是平行四边形;
(2)四边形是矩形,理由如下:
,是边上的中线,
,即,
又四边形是平行四边形,
四边形是矩形;
(3)当满足,时,四边形是正方形,
由(2)可知,当时,四边形是矩形,
在中,是边上的中线,
,
四边形是正方形,.
【题型9 由正方形性质与判定求线段长度】
1.
【分析】先利用勾股定理得到,进而证明四边形是正方形,则可得到,过点K作,延长分别交于L、S,则,利用勾股定理得到;证明四边形是矩形,得到,由对称性可知,则;证明四边形是矩形,得到,;如图所示,过点M作于W,则四边形是矩形,可得,再证明,得到,则,即点H,M之间的距离是.
【详解】解:∵点E,F是正方形边,
∴,
∴,,
同理可得,
∴,
∴四边形是正方形,
∵四边形各边的三等分点的连线为边,分别向内作等边三角形,
∴,
如图所示,过点K作,延长分别交于L、S,
∴,
∴;
∵,
∴四边形是矩形,
∴,
由对称性可知,
∴;
∵K、L分别为正方形边的中点,
∴,
∴四边形是矩形,
∴,;
如图所示,过点M作于W,则四边形是矩形,
∴,
∵,
∴,
∴,
∴,
∴点H,M之间的距离是,
故答案为:.
2.
【分析】本题考查了正方形的判定与性质,全等三角形的判定与性质,勾股定理等知识.熟练掌握正方形的判定与性质,全等三角形的判定与性质,勾股定理是解题的关键.
如图,作于,于,则四边形是矩形,证明,则,,可得四边形是正方形,则,设,则,,由,可求,则,由勾股定理得,,计算求解即可.
【详解】解:如图,作于,于,则四边形是矩形,
∴,即,
∴,
又∵,,
∴,
∴,,
∴四边形是正方形,
∴,
设,则,,
∴,
解得,,
∴,
由勾股定理得,,
故答案为:.
3.(1)证明:连接交于点,
由题意得,,
∵,
∴,
∴,
∵,
∴是线段的垂直平分线,
∴点是线段的中点,
∵点O是边的中点,
∴是的中位线,
∴;
(2)证明:延长交于点,
由(1),是线段的垂直平分线,
∴,
由题意得,
∴,
∵,,
∴,
∴垂直平分;
(3)解;当时,则点在线段的垂直平分线上,作于点,如图,
由题意得,,
∴,,
∴是等腰直角三角形,
∴,
∵,
∴,
∴是等腰直角三角形,
∴,
∴;
当时,如图,
由题意得,
∵,,
∴,
∴是等腰直角三角形,
∴,
∵,
∴四边形是正方形,
∴;
当时,如图,
∵,,,
∴,
∴,
∵,
∴在同一直线上,
设,
∴,,
在中,,即,
解得,
∴;
综上,线段的长度为1或或.
4.
【分析】过点作于点,作于点,利用定理证出,再根据全等三角形的性质可得;连接,根据正方形的性质、利用定理证出,推出,,再利用勾股定理可得,然后根据垂线段最短求出的最小值,由此即可得.
【详解】解:如图,过点作于点,作于点,
四边形为正方形,
,,
,且,
四边形为正方形,
,,
,
四边形是矩形,
,
,
,
在和中,,
,
,
矩形为正方形.
如图,连接,
四边形为正方形,,
,
,
矩形为正方形,
,
,
,
在和中,,
,
,
,
,
由垂线段最短可知,当时,取得最小值,最小值为,
的最小值为.
故答案为:
【题型10 由正方形性质与判定求角度】
1.(1)证明:如下图所示:
作EP⊥CD于P,EQ⊥BC于Q,
∵∠DCA=∠BCA,
∴EQ=EP,
∵∠QEF+∠FEC=90°,∠PED+∠FEC=90°,
∴∠QEF=∠PED,
在Rt△EQF和Rt△EPD中,
,
∴Rt△EQF≌Rt△EPD(ASA),
∴EF=ED,
∴矩形DEFG是正方形;
(2)如图2:
在Rt△ABC中AC=AB=,
∵EC=2,
∴AE=CE,
∴点F与C重合,此时△DCG是等腰直角三角形,
∴;
(3)①如图3:
当DE与AD的夹角为40°时,
∠DEC=45°+40°=85°,
∵∠DEF=90°,
∴∠CEF=5°,
∵∠ECF=45°,
∴∠EFC=130°,
②如图4:
当DE与DC的夹角为40°时,
∵∠DEF=∠DCF=90°,
∴∠EFC=∠EDC=40°,
综上所述,∠EFC=130°或40°.
2.(1)证明:在和中,
,
∴;
∴,
同理,
∴,
∵,
∴,
∴,
∴,
∴,
∴四边形是菱形;
(2)解:由(1)知四边形是菱形,
又∵,
∴四边形是正方形.
∴,
∴,
∵,
∴,
∴,
∴;
∴,
∵四边形是正方形,
∴,
由三角形的外角性质得:,
∴度数为的度数2倍的角有:,,,.
3.(1)解:如图,四边形ABCD为所求;
连接AD、DC、BC,所得四边形即为所作正方形;
(2)解:如图,∠BAC即为所求.
理由如下:
∵四个全等的矩形被对角线分成的直角三角形全等,
∴.
∴四边形ABCD是菱形.
又∵(SAS),
∴.
∵,
∴.
∴四边形ABCD是正方形,连接AC.
∴△ABC是等腰直角三角形.
∴.
4.(1)证明:∵是由旋转得到,
∴,,
∴,
∴,
∴平分.
(2)解:结论:.
由旋转的性质可知,,
∵,,
∴,
∵,
∴,
∴,
∵,
∴,
∴.
(3)解:如图,连接,过点B作交的延长线于H,作于T,
∵,
∴四边形为矩形,
∴,
∴,
∵,
∴,
∴,
∴四边形为正方形,
∴,
∵,
∴,
,,
,
∴,
∴,
∵,,
∴,
∴,
∴,
根据解析(2)可知,,
∴.
【题型11 由正方形性质与判定求面积】
1.问题一: ,
证明如下:在 和 中,
因为 ,
且 ,
所以 ,又因为 , ,
所以 ,所以 ;
问题二:
如图,连接,
因为点O是正方形的中心,所以,
又由问题一可知,,所以,
所以;
问题三:四边形是正方形,
证明如下:由问题一知,,所以,
所以由勾股定理知,所以四边形是菱形,
又因为在和中,对应边均相等,所以两个三角形全等,所以,
所以,所以,所以四边形是正方形.
2.解:新建的四边形为正方形.新广场的面积是原广场面积的5倍.
理由:四边形为正方形,
,,
.
,,,,
,
,
.
在和中
,
,
,,.
,
,
即,
同理可得,,
,
,
四边形为菱形.
,
菱形为正方形.
设原来正方形边长为,则新建的正方形边长为:.
新建的面积是原广场面积的5倍.
3.(1)证明:过点D作,交的延长线于点M,
∵,
∴,
∴四边形是矩形,
∴,,
∴,
∴,
又∵,,
∴,
∴,
∴;
(2)解:由(1)得:,
∴矩形是正方形
∵,
∴,
∴
∴
,
∴四边形的面积为.
4.(1)解:①有一个内角为45°的平行四边形,没有的内角,不是对角直角四边形;②矩形的对角为,是对角直角四边形;③菱形的对角不一定为,不是对角直角四边形;④直角梯形,的邻角为,但对角不一定为,不是对角直角四边形.
故答案为:②.
(2)①证明:∵.四边形是菱形,
∴,即,
∵是等腰直角三角形,
∴,
∴,
∴四边形是对角直角四边形;
②如图:过N作于H,于G,
∴,
∴四边形是矩形,
∴,
∵,
∴,
∵,,
∴,
∴,
∴四边形是正方形,
∴四边形的面积=正方形的面积.
【题型12 由正方形性质与判定证明】
1.(1)解:.
∵是正方形,
∴,
∵,
∴,
∴;
(2)解:①补全图形如图,
②四边形是正方形.
∵H、I、J、K分别是的中点,
∴,
∵,
∴,
∴四边形是菱形,
∵,
∴,
∵,
∴,
∴,
∴,
∴四边形是正方形.
2.
【分析】将绕点顺时针旋转,得到,连接,利用旋转的性质得到,,,由等腰直角三角形性质可得,利用勾股定理得到,进而得到,由勾股定理逆定理可知,,最后根据,即可求得.
【详解】解:将绕点顺时针旋转,得到,连接,
,
,,
,,,
,
,
,
,,
,
是直角三角形,且,
,
故答案为:.
3.证明:∵四边形ABCD为正方形,
∴,,
∵,
∴,
在与中,
,
∴,
同理可证:,
∴,
∴四边形EFMN为菱形,
∵,
∴,
∵,
∴,
∴,
∴,
∴四边形EFMN为正方形.
4.解:(1)四边形是菱形
理由如下:
∵,,
∴四边形是平行四边形,
∵四边形是矩形,
∴,,,
∴,
所以四边形是菱形 ;
(2)(1)中的结论不成立;
理由如下:
同(1),得四边形是平行四边形,
∵四边形是菱形,
∴,
∴,
∴四边形是矩形
(3)四边形是正方形;
理由如下:
同(1),得四边形是平行四边形,
∵四边形是正方形,
∴,,,,
∴,,
∴四边形是正方形.
【题型1 正方形与矩形、菱形的性质的区别与练习】
1.学习了四边形之后,小颖同学用如下图所示的方式表示了四边形与特殊四边形的关系,则图中的“M”和“N”分别表示( )
平行四边形,正方形 B.正方形,菱形
C.正方形,矩形 D.矩形,菱形
2.下列性质中,矩形、正方形都具有,但是菱形却不具有的性质是( )
A.对角线长度相等 B.对角线互相垂直
C.对角线互相平分 D.一组对角线平分一组对角
3.用两块完全重合的等腰直角三角形纸片拼下列图形:(1)平行四边形(不包含菱形、矩形、正方形);(2)矩形;(3)正方形;(4)等边三角形;(5)等腰直角三角形,一定能拼成的图形是( )
A.(1)(2)(3) B.(1)(3)(5)
C.(2)(3)(5) D.(1)(3)(4)(5)
4.如图,在平行四边形中,E、F是对角线上的两点(不与点A、C重合),且,分别连接,则下列结论错误的是( )
A.四边形是平行四边形
B.若四边形是菱形,那么四边形也是菱形
C.若四边形是正方形,那么四边形是菱形
D.若四边形是矩形,那么四边形也是矩形
【题型2 由正方形的性质求角度】
1.如图,在正方形中,点、分别为边、上的点,连接、,平分,若.当时,则的度数为( )
A. B.
C. D.
2.如图,正方形中,点分别在上,,经过对角线的中点O,若,则一定等于( )
A. B. C. D.
3.如图,在正方形中,点在对角线上,且;延长交于点,连接,则的度数为 .
4.如图,正方形的对角线与交于点,点为边上一点,连接,过点作于点,连接,若,则的度数为( )
A. B. C. D.
【题型3 由正方形的性质求线段长】
1.如图,在边长为4的正方形中,点是上一点,点是延长线上一点,连接,,平分.交于点.若,则的长度为( )
A.2 B. C. D.
2.如图,将正方形放在平面直角坐标系中,是原点,的坐标为则点的坐标为 ( )
A. B.
C. D.
3.如图,正方形和正方形中,点在上,,,于点,那么的长是( )
A. B. C. D.
4.如图,在边长为6的正方形中,点E,F分别是边上的动点,且满足,与交于点O,点M是的中点,G是边上的点,,则的最小值是( )
A.4 B.5 C.8 D.10
【题型4 由正方形的性质求面积】
1.如图,有一块边长为4的正方形(四条边相等,四个角是直角)塑料模板,将一块足够大的直角三角板的直角顶点落在点,两条直角边分别与交于点,与的延长线交于点,则四边形的面积是 .
2.《九章算术》中有一问题:“今有勾三步,股四步,问勾中容方几何?”意思是:如图1,直角三角形中,,,,求内接正方形的边长.我国数学家刘徽用“出人相补”原理将直角三角形补成知形(如图1),在该图形中发现一个与正方形面积相等的图形,从而求得这个正方形的边长.若点在线段上平移至点,连接,与直线分别相交于点,点(如图2),则平行四边形的面积为( )
A.12 B. C.25 D.
3.如图,一个正方形中有两个小正方形,如果它们的面积分别为,,则 (填“”或“=”或“”).
4.如图,以直角的每一条边为边长,在AB的同侧作三个正方形,各个涂色部分分别用①、②、③、④、⑤表示,已知②、④两部分的面积和为,则③、⑤两部分的面积和为( ).
A.8 B.9 C.10 D.11
【题型5 正方形中的折叠问题】
1.如图,正方形纸片的边长为12,是边上一点,连接,点在上,沿折叠,使点落在上的点,若,则的长为 .
2.如图,将边长为8的正方形纸片沿对折再展平,沿折痕剪开,得到矩形和矩形,再将矩形绕点顺时针方向旋转.使点与点重合,点的对应点为,则图②中阴影部分的周长为( )
A.9 B.10 C.16 D.20
3.如图,在正方形中,,点E,F分别在边上,.若将四边形沿折叠,点B恰好落在边上,则的长度为( )
A.1 B. C. D.2
4.如图,取一张矩形的纸片进行折叠,具体操作过程如下:
(1)【课本再现】
第一步:如图1,对折矩形纸片,使与重合,折痕为,把纸片展平;
第二步:在上选一点P,沿折叠纸片,使点A落在矩形内部的点M处,连接,根据以上操作,当点M在上时,___________;
(2)【类比应用】
如图2,现将矩形纸片换成正方形纸片,继续探究,过程如下:将正方形纸片按照(1)中的方式操作,并延长交于点Q,连接,当点M在上时,求的度数;
(3)【拓展延伸】
在(2)的探究中,正方形纸片的边长为,改变点P在上的位置(点P不与点A,D重合),沿折叠纸片,使点A落在矩形内部的点M处,连接,并延长交于点Q,连接.当时,请求出的长.
【题型6 正方形中的证明】
1.如图,在正方形纸片中,P为正方形边上的一点(不与点A,D重合),将正方形纸片折叠,使点B落在点P处,点C落在点G处,交于点H,折痕为,连接,,交于点M,连接.
(1)求证:平分;
(2)求证:;
(3)探究,与的数量关系,并说明理由.
2.已知;正方形的边长是4,F是边的中点,E是上的点,且,如图,求证:.
3.正方形的边长为6,正方形的顶点E、F分别在正方形的对角线和边上,,连接.
(1)求证:;
(2)求的值.
4.【阅读材料】
在学习正方形时,我们遇到过这样的问题:如图1,在正方形中,点E、F、G、H分别在、、、上,且,垂足为M,那么与相等吗?
分别过点G、H作、,垂足分别为P、Q,通过证明,得到.
根据阅读材料,完成下面探究1、探究2中的问题.
【探究1】
如图2,在正方形中,点E在上,使用无刻度的直尺和圆规作,交于点F(要求直尺、圆规各使用一次),保留作图痕迹,并标出点F,不要求写作法;
【探究2】
如图3,在正方形中,点E、F分别在、上,将正方形沿着翻折,点B、C分别落在、处,且经过点D,将纸片展开,延长交于点G,连接交于点M.
(1)求证:;
(2)求证:.
【题型7 正方形与矩形、菱形的判定定理的区别】
1.甲,乙两位同学采用折叠的方法,判断两张四边形纸片是否为正方形.
甲:如图①进行两次折叠,每次折叠后折痕两侧部分能完全重合,故判断原四边形是正方形;
乙:如图②进行两次折叠,每次折叠后折痕两侧部分能完全重合,故判断原四边形是正方形.
下列判断正确的是( )
A.仅甲正确 B.仅乙正确 C.甲、乙均正确 D.甲、乙均错误
2.下列命题:
①对角线相等的菱形是正方形;
②对角线互相垂直平分且相等的四边形是正方形;
③对角线互相垂直且相等的平行四边形是正方形;
④对角线互相垂直的矩形是正方形;
其中是真命题的个数是( )
A.个 B.个 C.个 D.个
3.如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边上的中点,连结AC、BD,回答问题
(1)对角线AC、BD满足条件 时,四边形EFGH是矩形.
(2)对角线AC、BD满足条件 时,四边形EFGH是菱形.
(3)对角线AC、BD满足条件 时,四边形EFGH是正方形.
4.如图,已知四边形是平行四边形,下列结论中不正确的是( )
A.当时,它是菱形 B.当时,它是菱形
C.当时,它是矩形 D.当时,它是正方形
【题型8 证明四边形是正方形】
1.如图1,四边形为正方形,为对角线上一点,连接,.
(1)求证:;
(2)如图2,过点作,交边于点,以,为邻边作矩形,连接.
求证:矩形是正方形;
若正方形的边长为,,求正方形的边长.
2.如图,在矩形中,是边上一点,是的延长线上一点,连接,,已知,.
(1)求证:四边形是正方形.
(2)若,,求四边形的面积.
3.问题情境:数学活动课上,同学们开展了以“矩形纸片折叠”为主题的探究活动(每个小组的矩形纸片规格相同),已知矩形纸片宽.
(1)如图1,小组将矩形纸片折叠,点落在边上的点处,折痕为,连接,然后将纸片展平,得到四边形.求证:四边形是正方形;
(2)如图2,小组将矩形纸片对折使与重合,展平后得到折痕,再次过点折叠使点落在折痕上的点处,得到折痕,连结,展平后得到四边形,求四边形的面积;
4.综合与实践
问题解决:
(1)如图1,在中,是边上的中线,是的中点,过点作,交的延长线于点,连接.求证:四边形是平行四边形.
类比迁移:
(2)如图2,在(1)的条件下,当时,试判断四边形的形状,并说明理由.
拓展应用:
(3)当满足什么条件时,四边形是正方形?请直接写出结论,不必证明.
【题型9 由正方形性质与判定求线段长度】
1.正方形工整、匀称、美观,设计方便,在人们的生活和生产实际中有着广泛的应用.如图1为某园林石窗,其外框为边长为6的正方形(如图2),点E,F,G,H分别为边上的中点,以四边形各边的三等分点的连线为边,分别向内作等边三角形(如),四个等边三角形的顶点恰好是正方形MNPQ各边的中点,则点H,M之间的距离是 .
2.如图,在四边形中,,,,,则对角线的长为 .
3.综合与实践
问题情境:“综合与实践”课上,老师提出如下问题:如图1,在中,,点O是边的中点,连接.保持不动,将从图1的位置开始,绕点O顺时针旋转得到,点A,D,C的对应点分别为点E,F,G.当线段与线段相交于点M(点M不与点A,B,F,G重合)时,连接.老师要求各个小组结合所学的图形变换的知识展开数学探究.
(1)初步思考:如图2,连接,“勤学”小组在旋转的过程中发现,请你证明这一结论;
(2)操作探究:如图3,连接,“善思”小组在旋转的过程中发现垂直平分,请你证明这一结论;
(3)拓展延伸:已知,,在旋转的过程中,当以点F,C,D为顶点的三角形是等腰三角形时,请直接写出此时线段的长度.
4.如图,已知四边形是正方形,,点E为对角线上一动点,连接,过点E作,交射线于点F,以,为邻边作矩形,连,的最小值为 .
【题型10 由正方形性质与判定求角度】
1.四边形 ABCD 为正方形,点 E 为线段 AC 上一点,连接 DE,过点 E 作 EF ⊥DE,交射线 BC 于点 F,以 DE、EF 为邻边作矩形 DEFG,连接 CG.
(1)如图,求证:矩形 DEFG 是正方形;
(2)若 AB=,CE=2,求 CG 的长;
(3)当线段 DE 与正方形 ABCD 的某条边的夹角是 40°时,直接写出∠EFC 的度数.
2.已知:是的角平分线,点在边上,,过点作,交于点,连接.
(1)如图1,求证:四边形是菱形;
(2)如图2,当时,在不添加任何辅助线的情况下,请直接写出图2中度数为的度数2倍的角.
3.如图,用四个完全相同的矩形拼成了一个大正方形,AB是其中一个小矩形的对角线,请在大正方形中完成下列画图,要求:①仅用无刻度的直尺;②保留必要的画图痕迹.
(1)在图中画出一个以AB为边的正方形;
(2)在图中画出一个以点A或点B为顶点,AB为一边的45°角,并说明理由.
4.如图,在中,,将绕点C顺时针旋转得到,点B的对应点为E,点A的对应点D落在线段上,与相交于点F,连接.
(1)求证:平分;
(2)试判断与的位置关系,并说明理由;
(3)若,求的大小.(直接写出结果即可)
【题型11 由正方形性质与判定求面积】
1.【问题一】如图①,正方形的对角线相交于点O,点O又是正方形的一个顶点, 交于点E, 交于点F,则与的数量关系为______;
【问题二】受图①启发,兴趣小组画出了图②:直线m、n经过正方形的对称中心O,直线m分别与交于点E、F,直线n分别与交于点G、H,且 ,若正方形边长为8,求四边形的面积;
【问题三】在图②中,连接E、G、F、H四点,请证明四边形是正方形.
2.如图,阴影部分是一个正方形广场,规划将正方形的四边各延长一倍,即、、、,将M、N、P、Q四点连接,建成新的广场,试问建成的新广场是什么形状,并且它的面积是原广场的多少倍?
3.已知,如图,在四边形中,,,,垂足为点E.
(1)求证:;
(2)若,,求四边形的面积.
4.我们知道:有一个角是直角的三角形叫做直角三角形.类似地,我们定义:至少有一组对角是直角的四边形叫做对角直角四边形.
(1)下列图形:①有一个内角为的平行四边形;②矩形;③菱形;
④直角梯形,其中对角直角四边形是 (只填序号);
(2)如图,菱形的对角线,相交于点,在菱形的外部以为斜边作等腰直角,连接.
①求证:四边形是对角直角四边形;
②若点到的距离是2,求四边形的面积.
【题型12 由正方形性质与判定证明】
1.如图①,在正方形中,点分别在上且.
(1)试探索线段的大小关系,写出你的结论并说明理由;
(2)连接,分别取的中点,顺次连接,得到四边形:
①请在图②中补全图形;
②四边形是什么特殊平行四边形?请说明理由.
2.如图,若点是正方形外一点,且,,,则 °.
3.如图,E,F,M,N分别是正方形四条边上的点,且.试判断四边形是什么图形,并证明你的结论.
4.问题情境:通过对《平行四边形》一章内容的学习,我们认识到矩形、菱形、正方形都是特殊的平行四边形,它们除了具有平行四边形的性质外,还有各自的特殊性质.根据它们的特殊性,得到了这些特殊的平行四边形的判定定理.数学课上,老师给出了一道题:如图①,矩形的对角线,交于点O,过点D作,且,连接.
初步探究:
(1)判断四边形的形状,并说明理由.
深入探究:
(2)如图②,若四边形是菱形,(1)中的结论还成立吗?请说明理由.
拓展延伸:
(3)如图③,若四边形是正方形,四边形又是什么特殊的四边形?请说明理由.
参考答案
【题型1 正方形与矩形、菱形的性质的区别与练习】
1.B
【分析】本题考查了特殊的平行四边形,正确理解矩形,菱形,正方形之间的关系是解题的关键.
根据特殊的平行四边形的概念判断即可.
【详解】解:∵矩形和菱形是特殊的平行四边形,正方形即是菱形也是矩形,
∴是正方形,是菱形,
故选:B
2.A
【分析】利用正方形的性质,矩形的性质,菱形的性质依次判断可求解.
【详解】解:菱形具有的性质是:两组对边分别平行,对角线互相平分,对角线互相垂直;
矩形具有的性质是:两组对边分别平行,对角线互相平分,对角线相等;
正方形具有菱形和矩形的性质,
故选项B,C,D不符合题意;
菱形不具有的性质为:对角线长度相等,
故选项A符合题意.
故选:A.
3.B
【分析】通过不同的组合方法,得出不同的图形.
【详解】解:用两块完全重合的等腰直角三角形纸片可以拼成下列图形:
(1)平行四边形
(3)正方形
(5)等腰直角三角
故选B.
4.D
【分析】本题考查了平行四边形的判定和性质,菱形的判定和性质,矩形的判定和性质, 正方形的性质,熟练掌握这些知识是解题的关键.连接交于点O,根据平行四边形的性质可得, 再根据E、F是对角线上的两点(不与点A、C重合),,可得,进一步即可判断A选项; 根据菱形的性质可得,进一步即可判断选项; 根据正方形的性质可得,进一步即可判断选项;根据矩形的性质可得, 再根据E、F是对角线上的两点 (不与点A、C重合),可得,进一步可判断选项.
【详解】解:连接交于点O,如图所示:
∵四边形是平行四边形,
∴,
∵E、F是对角线上的两点(不与点A、C重合), ,
∴,
∵,
∴四边形是平行四边形,故A不符合题意;
当四边形是菱形时, ,
∴,
又∵四边形是平行四边形,
∴四边形是菱形,
故不符合题意;
当四边形是正方形时, ,
∴,
又∵四边形是平行四边形,
∴四边形是菱形,
故不符合题意;
当四边形是矩形时, ,
∵E、F是对角线上的两点(不与点A、C重合),
∴,
∴四边形不是矩形,
故符合题意,
故选:.
【题型2 由正方形的性质求角度】
1.C
【分析】本题考查了正方形的性质,角平分线的定义,全等三角形的判定和性质,由正方形的性质可得,,,进而由可得,,再由角平分线的定义得,又证明可得,最后利用角的和差关系即可求解,掌握正方形的性质是解题的关键.
【详解】解:∵四边形是正方形,
∴,,
∵,
∴,
∴,
∵平分,
∴,
在和中,
,
∴,
∴,
∴,
故选:.
2.B
【分析】证明,可得,利用直角三角形斜边上的中线等于斜边的一半,可得,则可得,利用三角形外角和定理,即可得到的值.
【详解】解:四边形是正方形,
,
经过对角线的中点O,
,
在与中,
,
,
,
,
,
,
,
故选:B.
3.
【分析】根据正方形的性质可得,,再根据又证得,得,,根据三角形内角和定理求得,最后根据平角定义求得答案.
【详解】解:正方形,
,,
又,
,
,,
,
,
,
故答案为:.
4.C
【分析】本题主要考查了正方形的性质,直角三角形斜边上的中线等于斜边的一半,等边对等角以及三角形外角性质等知识,取中点G,连接,,设与交于点,证明,得,证明,求出,根据可得,整理后可得结论
【详解】解:取中点G,连接,,设与交于点,如图,
∵四边形是正方形,
∴,,
∴,,
又,
∴
∴
∴
∵,
∴,
∵
∴
在和中,
∴,
∵,且,
∴
∴
而
又
∴
∴.
故选:C.
【题型3 由正方形的性质求线段长】
1.D
【分析】本题主要考查了正方形的性质,全等三角形的性质与判定,勾股定理,先由正方形的性质得到,再证明得到,进一步证明得到,设,则,
在中,由勾股定理得,解方程即可得到答案.
【详解】解:∵四边形是正方形,
∴,
又∵,
∴,
∴,
∵平分,
∴,
又∵,
∴,
∴,
设,则,
在中,由勾股定理得,
∴,
解得,
∴,
故选:D.
2.D
【分析】过点作轴于,过点作的延长线于,交y轴于点,由可证,可得,,据此即可求解.
【详解】解:如图,过点作轴于,过点作的延长线于,交y轴于点,
点的坐标为,
,,
∵轴轴,
∴四边形是矩形,
∴
四边形是正方形,
,,
,,
,
,
,
在和中,
,
,
,,
,
点的坐标为,
故选:D.
3.D
【分析】本题考查了正方形的性质,勾股定理,直角三角形的面积,连接,由正方形的性质得到,,利用勾股定理可求得,,,再根据三角形的面积得到,代入已求计算即可求解,由正方形的性质得到是解题的关键.
【详解】解:连接,
∵正方形和正方形,
∴,,
∵,,
∴,,,
∴,
∵,
∴,
即,
解得,
故选:.
4.B
【分析】本题主要考查了正方形的性质,全等三角形的性质与判定,直角三角形的性质,勾股定理等等,先证明得到,进而得到,则由直角三角形的性质可得,如图所示,在延长线上截取,连接,易证明,则,可得当H、D、F三点共线时,有最小值,即此时有最小值,最小值即为的长的一半,求出,在中,由勾股定理得,责任的最小值为5.
【详解】解:∵四边形是正方形,
∴,
又∵,
∴,
∴,
∴,
∵点M是的中点,
∴;
如图所示,在延长线上截取,连接,
∵,
∴,
∴,
∴,
∴当H、D、F三点共线时,有最小值,即此时有最小值,最小值即为的长的一半,
∵,,
∴,
∴,
在中,由勾股定理得,
∴的最小值为5,
故选:B.
【题型4 由正方形的性质求面积】
1.16
【分析】证明,得到,计算即可.
【详解】∵正方形,
∴,,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
故答案为:16.
2.B
【分析】本题考查了正方形和矩形的性质,正确列出方程是解答本题的关键.设正方形的边长为x,证明,则,得到 解得,即可求出正方形的边长为,即可得到答案.
【详解】如图1,设正方形的边长为x,
根据题意得,四边形都是矩形,
∴
∴
∴
∵,,
∴
∴
解得,
∴正方形的边长为,
∴正方形的边长为,
∵平行四边形的面积
故选:B.
3.
【分析】本题考查了正方形的性质,勾股定理等等知识,设正方形的边长为6,然后求出与的值,问题得解.
【详解】解:如图,设正方形的边长为6,
∵是正方形的对角线,
,,
∴,
又∵四边形与四边形是正方形,
,,
,,
,,
∴.
故答案为:.
4.B
【分析】设序号为①,②,③,④,⑤图形的面积分别为,,,,,利用正方形性质,三角形全等证明即可,本题考查了正方形的性质,勾股定理,三角形全等的判定和性质,熟练掌握正方形的性质,勾股定理是解题的关键.
【详解】如图所示,
设序号为①,②,③,④,⑤图形的面积分别为,,,,,,
根据题意,得,
四边形是正方形,,
,
,,
,
,
.
∴
∵②、④两部分的面积和为,
∴,
四边形是正方形,四边形是正方形,
,
,
.
∴,
根据题意,得
,
故选B.
【题型5 正方形中的折叠问题】
1.
【分析】本题考查了正方形的性质,轴对称的性质 ,全等三角形的判定与性质,勾股定理,面积法求线段的长度等,解题关键是能够灵活运用正方形的性质和轴对称的性质.
由折叠及轴对称的性质可知, 垂直平分, 先证推出的长,再利用勾股定理求出的长, 最后在中利用面积法可求出的长,可进一步求出的长,的长.
【详解】解:设与交于点M,
在正方形中,
,
在中,,
∵由折叠的性质可得
,
∴垂直平分,
,
∵,
所以,
又∵,,
∴,
∴,
又∵,
故答案为:
2.D
【分析】本题主要考查全等三角形的判定与性质,勾股定理以及菱形的判定与性质等,解答本题的关键是勾股定理以及菱形的判定.首先根据已知条件判断出,得到,,然后可设的长度为x,则,根据勾股定理列方程可解出x,最后证明阴影部分是菱形后,即可求出其周长.
【详解】解:如图,设交于G,旋转后交于点H,
由题意知,,,
又∵,
∴,
∴,,
设,则,
在中,,
解得:,
∴,
∵,,
∴四边形为平行四边形,
又∵,
∴为菱形,
∴阴影部分的周长为:,
故选:D.
3.D
【分析】本题考查正方形的性质,折叠的性质,含30度角的直角三角形的性质,解题的关键是熟练运用以上性质;根据可得根据折叠后对应角相等、对应边相等,可得,进而可得,根据含30度角的直角三角形的性质可得,设,则,列方程求解即可.
【详解】解:四边形是正方形,
将四边形沿折叠,点B恰好落在边上,
,
,
设,则,
,
,
,
故选:D.
4.(1)解:如图,连接,
∵对折矩形纸片,使与重合,折痕为,
∴垂直平分,
∴,,
∵沿折叠纸片,使点落在矩形内部的点处,
∴,,
∴,
∴是等边三角形,
∴,
∴,
故答案为:;
(2)解:如图,
同(1)可证,
∴,
在正方形中,,,
由折叠知,,
∴,,
在和中,
,
∴,
∴,
∴
(3)解:当点Q在点F的下方时,如图,
∵正方形中,,
∴,
∴,
由(2)知,
∴,
设,由折叠知,
∴,,
在中,,
∴,
解得,即;
当点Q在点F的上方时,如图,
则,
∴,
∴,
设,
则,,
在中,,
∴,
解得,即;
综上可知,的长为或.
【题型6 正方形中的证明】
1.(1)证明:由题意,得,
∴.
∵四边形是正方形,
∴,
∴,即.
又∵,
∴,
∴,即平分.
(2)证明:如图1,过点F作于点K,设交于点O.
∵,
∴四边形是矩形,
∴.
∵点B与点P关于对称,
∴,
∴,
∴.
∵,
∴.
∵,
∴,
∴.
(3)解:.
理由:如图,过点B作,垂足为Q.
由(1)知,.
∵,
∴.
∵,
∴,
∴.
又∵,
∴.
∵,
∴,
∴,
∴,
即.
2.证明:连接,延长交延长线于点G,如图:
∵正方形,
,
,
,
∴设,则,
在中,,
∵点F是中点,
∴,
∵,
,
,
,
,
又∵
.
3.(1)证明:∵正方形和,
∴,,,
∴,
∴,
∴;
(2)解:连接和,
∵正方形的边长为6,且,
∴,,,
∴,
由(1)得,,
∴,
∴,
∴.
4.解∶[探究1]
如图,即为所求,
∵四边形是正方形,
∴,,,
由作图知:,
∴,
∴,
∵,
∴,
∴;
[探究2]
(1)证明:∵翻折,
∴,,
又,
∴,
∴;
(2)连接,过F作于N,
则四边形是矩形,
∴,,
又,
∴,
∵翻折,
∴,
∵,,
∴,,
又,
∴,
∴,
又,
∴,
∴,
∵,
∴,
∴,
又,,
∴,
∴,
又,,
∴
【题型7 正方形与矩形、菱形的判定定理的区别与练习】
1.D
【分析】利用折叠的性质和菱形、矩形、正方形的判定即可得出答案.
【详解】解∶①按照图①折叠,可得四边形的四边相等,原四边形是菱形或正方形;
②按照图②折叠,可得四边形的四个角相等,不能得四条边相等,原四边形是矩形;
故选∶ D.
2.A
【分析】利用正方形的判定方法分别判断后即可确定正确的选项.
【详解】解:对角线相等的菱形是正方形,正确,是真命题,符合题意;
对角线互相垂直平分且相等的四边形是正方形,正确,是真命题,符合题意;
对角线互相垂直且相等的平行四边形是正方形,正确,是真命题,符合题意;
对角线互相垂直的矩形是正方形,正确,是真命题,符合题意.
真命题有个,
故选A.
3. AC⊥BD AC=BD AC⊥BD且AC=BD
【分析】先证明四边形EFGH是平行四边形,
(1)在已证平行四边形的基础上,要使所得四边形是矩形,则需要一个角是直角,故对角线应满足互相垂直
(2)在已证平行四边形的基础上,要使所得四边形是菱形,则需要一组邻边相等,故对角线应满足相等
(3)联立(1)(2),要使所得四边形是正方形,则需要对角线垂直且相等
【详解】解:连接AC、BD.
∵E、F、G、H分别是AB、BC、CD、DA边上的中点,
∴EF∥AC,EF=AC,FG∥BD,FG=BD,GH∥AC,GH=AC,EH∥BD,EH=BD.
∴EF∥HG,EF=GH,FG∥EH,FG=EH.
∴四边形EFGH是平行四边形;
(1)要使四边形EFGH是矩形,则需EF⊥FG,
由(1)得,只需AC⊥BD;
(2)要使四边形EFGH是菱形,则需EF=FG,
由(1)得,只需AC=BD;
(3)要使四边形EFGH是正方形,综合(1)和(2),
则需AC⊥BD且AC=BD.
故答案是:AC⊥BD;AC=BD;AC⊥BD且AC=BD
4.D
【分析】此题主要考查学生对正方形的判定、平行四边形的性质、菱形的判定和矩形的判定的理解和掌握,此题涉及到的知识点较多,学生答题时容易出错.
根据邻边相等的平行四边形是菱形;根据所给条件可以证出邻边相等;根据有一个角是直角的平行四边形是矩形;根据对角线相等的平行四边形是矩形.
【详解】解:A、根据邻边相等的平行四边形是菱形可知:四边形是平行四边形,当时,它是菱形,故A选项正确,不符合题意;
B、四边形是平行四边形,,
四边形是菱形,故B选项正确,不符合题意;
C、有一个角是直角的平行四边形是矩形,故C选项正确,不符合题意;
D、根据对角线相等的平行四边形是矩形可知当时,它是矩形,不是正方形,故D选项错误,符合题意.
故选:D.
【题型8 证明四边形是正方形】
1.(1)证明:∵四边形为正方形,
∴,,
在和中,
,
∴,
∴;
(2)①证明:如图,作于,于,则四边形为矩形,
∴,
∵点是正方形对角线上的点,
∴,
∵,
∴,
∵,
在和中
∴,
∴,
∵四边形是矩形,
∴矩形是正方形;
②解:正方形和正方形中,,,
,
∴,
∴,
∴,,
∵,
∴,
∴,
∴,
∵,
∴,
连接,
∴,
∴,
即正方形的边长为.
2.(1)证明:四边形是矩形,
,
,.
,
,
,
,
,
.
矩形是正方形.
(2)解:,,
,
.
.
3.(1)四边形是正方形,理由如下:
∵四边形是矩形,
∴,,
∴,
由第一步折叠可知:,
∴,
∴,
∴,
∴四边形是菱形,
又∵,
∴四边形是正方形;
(2)连接,
由折叠得,
∴
∴
∴是等边三角形,
∴
∴
设则,
由勾股定理得,
∴
解得,(负值舍去)
∴
由折叠得,,
∴.
4.证明:(1),
,
是的中点,
,
在和中,
,
,
,
是边上的中线,
,
,
又,
四边形是平行四边形;
(2)四边形是矩形,理由如下:
,是边上的中线,
,即,
又四边形是平行四边形,
四边形是矩形;
(3)当满足,时,四边形是正方形,
由(2)可知,当时,四边形是矩形,
在中,是边上的中线,
,
四边形是正方形,.
【题型9 由正方形性质与判定求线段长度】
1.
【分析】先利用勾股定理得到,进而证明四边形是正方形,则可得到,过点K作,延长分别交于L、S,则,利用勾股定理得到;证明四边形是矩形,得到,由对称性可知,则;证明四边形是矩形,得到,;如图所示,过点M作于W,则四边形是矩形,可得,再证明,得到,则,即点H,M之间的距离是.
【详解】解:∵点E,F是正方形边,
∴,
∴,,
同理可得,
∴,
∴四边形是正方形,
∵四边形各边的三等分点的连线为边,分别向内作等边三角形,
∴,
如图所示,过点K作,延长分别交于L、S,
∴,
∴;
∵,
∴四边形是矩形,
∴,
由对称性可知,
∴;
∵K、L分别为正方形边的中点,
∴,
∴四边形是矩形,
∴,;
如图所示,过点M作于W,则四边形是矩形,
∴,
∵,
∴,
∴,
∴,
∴点H,M之间的距离是,
故答案为:.
2.
【分析】本题考查了正方形的判定与性质,全等三角形的判定与性质,勾股定理等知识.熟练掌握正方形的判定与性质,全等三角形的判定与性质,勾股定理是解题的关键.
如图,作于,于,则四边形是矩形,证明,则,,可得四边形是正方形,则,设,则,,由,可求,则,由勾股定理得,,计算求解即可.
【详解】解:如图,作于,于,则四边形是矩形,
∴,即,
∴,
又∵,,
∴,
∴,,
∴四边形是正方形,
∴,
设,则,,
∴,
解得,,
∴,
由勾股定理得,,
故答案为:.
3.(1)证明:连接交于点,
由题意得,,
∵,
∴,
∴,
∵,
∴是线段的垂直平分线,
∴点是线段的中点,
∵点O是边的中点,
∴是的中位线,
∴;
(2)证明:延长交于点,
由(1),是线段的垂直平分线,
∴,
由题意得,
∴,
∵,,
∴,
∴垂直平分;
(3)解;当时,则点在线段的垂直平分线上,作于点,如图,
由题意得,,
∴,,
∴是等腰直角三角形,
∴,
∵,
∴,
∴是等腰直角三角形,
∴,
∴;
当时,如图,
由题意得,
∵,,
∴,
∴是等腰直角三角形,
∴,
∵,
∴四边形是正方形,
∴;
当时,如图,
∵,,,
∴,
∴,
∵,
∴在同一直线上,
设,
∴,,
在中,,即,
解得,
∴;
综上,线段的长度为1或或.
4.
【分析】过点作于点,作于点,利用定理证出,再根据全等三角形的性质可得;连接,根据正方形的性质、利用定理证出,推出,,再利用勾股定理可得,然后根据垂线段最短求出的最小值,由此即可得.
【详解】解:如图,过点作于点,作于点,
四边形为正方形,
,,
,且,
四边形为正方形,
,,
,
四边形是矩形,
,
,
,
在和中,,
,
,
矩形为正方形.
如图,连接,
四边形为正方形,,
,
,
矩形为正方形,
,
,
,
在和中,,
,
,
,
,
由垂线段最短可知,当时,取得最小值,最小值为,
的最小值为.
故答案为:
【题型10 由正方形性质与判定求角度】
1.(1)证明:如下图所示:
作EP⊥CD于P,EQ⊥BC于Q,
∵∠DCA=∠BCA,
∴EQ=EP,
∵∠QEF+∠FEC=90°,∠PED+∠FEC=90°,
∴∠QEF=∠PED,
在Rt△EQF和Rt△EPD中,
,
∴Rt△EQF≌Rt△EPD(ASA),
∴EF=ED,
∴矩形DEFG是正方形;
(2)如图2:
在Rt△ABC中AC=AB=,
∵EC=2,
∴AE=CE,
∴点F与C重合,此时△DCG是等腰直角三角形,
∴;
(3)①如图3:
当DE与AD的夹角为40°时,
∠DEC=45°+40°=85°,
∵∠DEF=90°,
∴∠CEF=5°,
∵∠ECF=45°,
∴∠EFC=130°,
②如图4:
当DE与DC的夹角为40°时,
∵∠DEF=∠DCF=90°,
∴∠EFC=∠EDC=40°,
综上所述,∠EFC=130°或40°.
2.(1)证明:在和中,
,
∴;
∴,
同理,
∴,
∵,
∴,
∴,
∴,
∴,
∴四边形是菱形;
(2)解:由(1)知四边形是菱形,
又∵,
∴四边形是正方形.
∴,
∴,
∵,
∴,
∴,
∴;
∴,
∵四边形是正方形,
∴,
由三角形的外角性质得:,
∴度数为的度数2倍的角有:,,,.
3.(1)解:如图,四边形ABCD为所求;
连接AD、DC、BC,所得四边形即为所作正方形;
(2)解:如图,∠BAC即为所求.
理由如下:
∵四个全等的矩形被对角线分成的直角三角形全等,
∴.
∴四边形ABCD是菱形.
又∵(SAS),
∴.
∵,
∴.
∴四边形ABCD是正方形,连接AC.
∴△ABC是等腰直角三角形.
∴.
4.(1)证明:∵是由旋转得到,
∴,,
∴,
∴,
∴平分.
(2)解:结论:.
由旋转的性质可知,,
∵,,
∴,
∵,
∴,
∴,
∵,
∴,
∴.
(3)解:如图,连接,过点B作交的延长线于H,作于T,
∵,
∴四边形为矩形,
∴,
∴,
∵,
∴,
∴,
∴四边形为正方形,
∴,
∵,
∴,
,,
,
∴,
∴,
∵,,
∴,
∴,
∴,
根据解析(2)可知,,
∴.
【题型11 由正方形性质与判定求面积】
1.问题一: ,
证明如下:在 和 中,
因为 ,
且 ,
所以 ,又因为 , ,
所以 ,所以 ;
问题二:
如图,连接,
因为点O是正方形的中心,所以,
又由问题一可知,,所以,
所以;
问题三:四边形是正方形,
证明如下:由问题一知,,所以,
所以由勾股定理知,所以四边形是菱形,
又因为在和中,对应边均相等,所以两个三角形全等,所以,
所以,所以,所以四边形是正方形.
2.解:新建的四边形为正方形.新广场的面积是原广场面积的5倍.
理由:四边形为正方形,
,,
.
,,,,
,
,
.
在和中
,
,
,,.
,
,
即,
同理可得,,
,
,
四边形为菱形.
,
菱形为正方形.
设原来正方形边长为,则新建的正方形边长为:.
新建的面积是原广场面积的5倍.
3.(1)证明:过点D作,交的延长线于点M,
∵,
∴,
∴四边形是矩形,
∴,,
∴,
∴,
又∵,,
∴,
∴,
∴;
(2)解:由(1)得:,
∴矩形是正方形
∵,
∴,
∴
∴
,
∴四边形的面积为.
4.(1)解:①有一个内角为45°的平行四边形,没有的内角,不是对角直角四边形;②矩形的对角为,是对角直角四边形;③菱形的对角不一定为,不是对角直角四边形;④直角梯形,的邻角为,但对角不一定为,不是对角直角四边形.
故答案为:②.
(2)①证明:∵.四边形是菱形,
∴,即,
∵是等腰直角三角形,
∴,
∴,
∴四边形是对角直角四边形;
②如图:过N作于H,于G,
∴,
∴四边形是矩形,
∴,
∵,
∴,
∵,,
∴,
∴,
∴四边形是正方形,
∴四边形的面积=正方形的面积.
【题型12 由正方形性质与判定证明】
1.(1)解:.
∵是正方形,
∴,
∵,
∴,
∴;
(2)解:①补全图形如图,
②四边形是正方形.
∵H、I、J、K分别是的中点,
∴,
∵,
∴,
∴四边形是菱形,
∵,
∴,
∵,
∴,
∴,
∴,
∴四边形是正方形.
2.
【分析】将绕点顺时针旋转,得到,连接,利用旋转的性质得到,,,由等腰直角三角形性质可得,利用勾股定理得到,进而得到,由勾股定理逆定理可知,,最后根据,即可求得.
【详解】解:将绕点顺时针旋转,得到,连接,
,
,,
,,,
,
,
,
,,
,
是直角三角形,且,
,
故答案为:.
3.证明:∵四边形ABCD为正方形,
∴,,
∵,
∴,
在与中,
,
∴,
同理可证:,
∴,
∴四边形EFMN为菱形,
∵,
∴,
∵,
∴,
∴,
∴,
∴四边形EFMN为正方形.
4.解:(1)四边形是菱形
理由如下:
∵,,
∴四边形是平行四边形,
∵四边形是矩形,
∴,,,
∴,
所以四边形是菱形 ;
(2)(1)中的结论不成立;
理由如下:
同(1),得四边形是平行四边形,
∵四边形是菱形,
∴,
∴,
∴四边形是矩形
(3)四边形是正方形;
理由如下:
同(1),得四边形是平行四边形,
∵四边形是正方形,
∴,,,,
∴,,
∴四边形是正方形.
