8.6.2 直线与平面垂直(第1课时) 课件(共26张PPT)-2024-2025学年高一数学(人教A版2019必修第二册)
文档属性
| 名称 | 8.6.2 直线与平面垂直(第1课时) 课件(共26张PPT)-2024-2025学年高一数学(人教A版2019必修第二册) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-22 22:23:18 | ||
图片预览




文档简介
(共26张PPT)
第八章立体几何初步
人教A版2019必修第二册
8.6.2 直线与平面垂直(第1课时)
理解直线与平面垂直的判定定理,并会对其进行简单的应 用,培养直观想象、逻辑推理的核心素养
理解直线与平面所成的角的概念,并能解决简单的线面角 问题,培养数学运算的核心素养
会求点到平面的距离,培养数学运算的核心素养.
学习目标
1
a//a
直线与平面平行
aNa=A
直线与平面相交
垂直 斜交
aCa
a a 直线在平面内
a
空间中直线与平面有几种位置关系
直线在平面外
afα
y 复习回顾
线面位 置关系
a
b
a
a
观察1 在日常生活中,我们对直线与平面垂直有很多感性认识.比如,旗 杆与底面的位置关系,教室里相邻墙面的交线与地面的位置关系,都给我 们以直线与平面垂直的形象.
y 新课导入
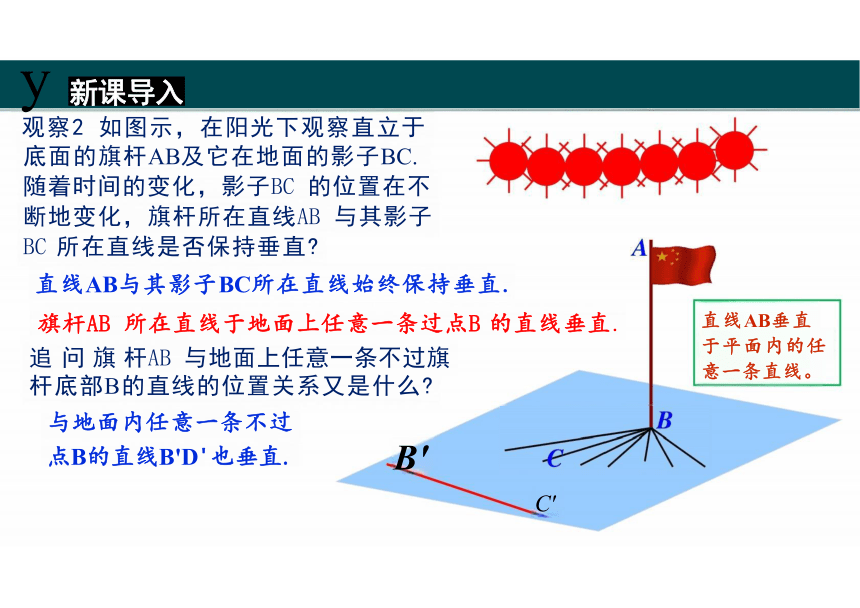
观察2 如图示,在阳光下观察直立于
底面的旗杆AB及它在地面的影子BC.
随着时间的变化,影子BC 的位置在不
断地变化,旗杆所在直线AB 与其影子
BC 所在直线是否保持垂直
直线AB与其影子BC所在直线始终保持垂直.
旗杆AB 所在直线于地面上任意一条过点B 的直线垂直.
追 问 旗 杆AB 与地面上任意一条不过旗
杆底部B的直线的位置关系又是什么
与地面内任意一条不过
点B的直线B'D'也垂直. B'
y
直线AB垂直 于平面内的任 意一条直线。
新课导入
C'
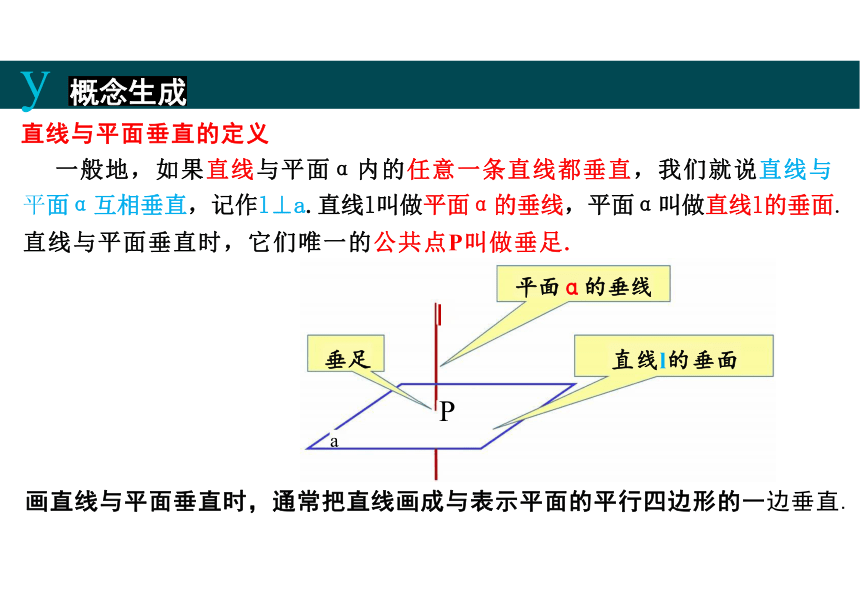
直线与平面垂直的定义
一般地,如果直线与平面α内的任意一条直线都垂直,我们就说直线与
平面α互相垂直,记作l⊥a.直线l叫做平面α的垂线,平面α叫做直线l的垂面. 直线与平面垂直时,它们唯一的公共点P叫做垂足.
平面α的垂线
l
垂足 直线l的垂面
P
a
y
画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.
概念生成
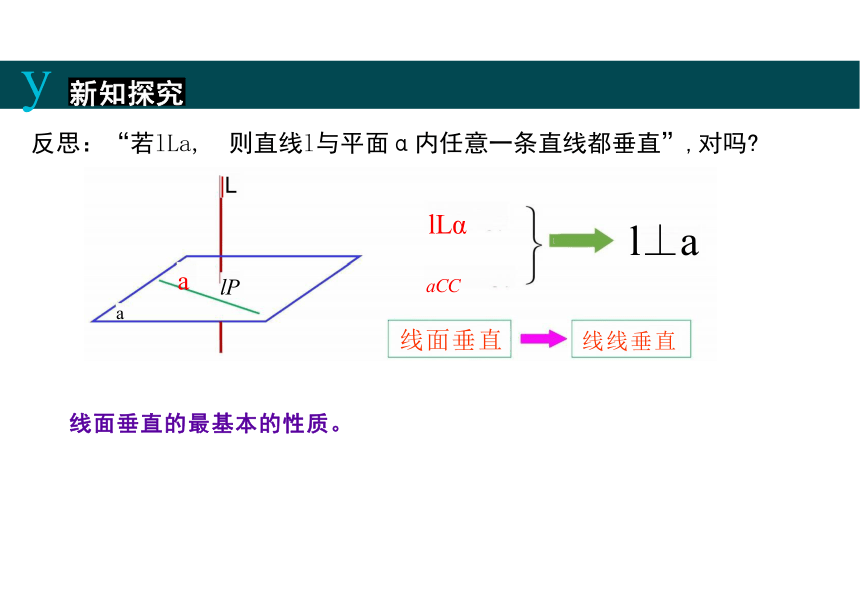
反思:“若lLa, 则直线l与平面α内任意一条直线都垂直”,对吗
|L
lLα l⊥a
a lP aCC
a
线面垂直 线线垂直
线面垂直的最基本的性质。
y
新知探究
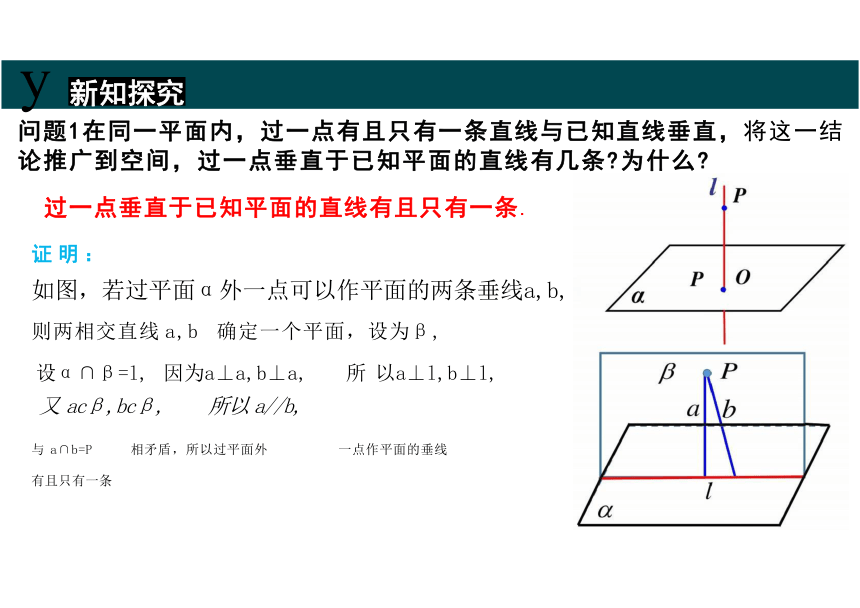
问题1在同一平面内,过一点有且只有一条直线与已知直线垂直,将这一结 论推广到空间,过一点垂直于已知平面的直线有几条 为什么
过一点垂直于已知平面的直线有且只有一条.
证 明 :
如图,若过平面α外一点可以作平面的两条垂线a,b,
则两相交直线 a,b 确定一个平面,设为β,
设α∩β=l, 因为a⊥a,b⊥a, 所 以a⊥l,b⊥l,
又 acβ,bcβ, 所以 a//b,
与 a∩b=P 相矛盾,所以过平面外 一点作平面的垂线
有且只有一条
y
新知探究
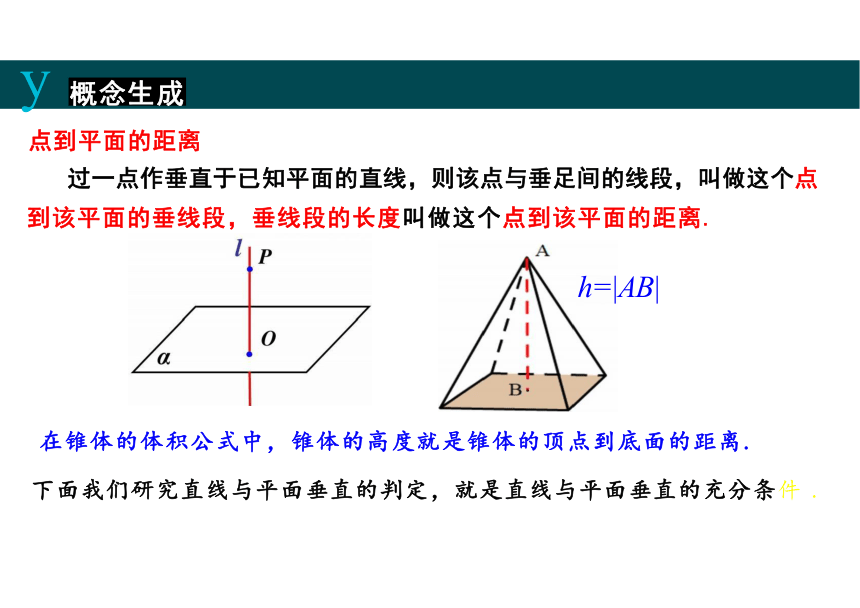
点到平面的距离
过一点作垂直于已知平面的直线,则该点与垂足间的线段,叫做这个点 到该平面的垂线段,垂线段的长度叫做这个点到该平面的距离.
h=|AB|
在锥体的体积公式中,锥体的高度就是锥体的顶点到底面的距离.
下面我们研究直线与平面垂直的判定,就是直线与平面垂直的充分条件 .
y
概念生成
问题2 怎么来判定直线与平面垂直 由定义判定直线与平面垂直,简便吗
能否只需验证直线与平面内部分直线垂直就能判定直线与平面垂直呢
探究准备一块三角形的纸片ABC, 过△ABC 的顶点A翻折纸片,得到折痕
AD, 将翻折后的纸片竖起放置在桌面上(BD,DC 与桌面接触).观察:
(1)折痕AD 与桌面垂直吗 不一定 当AD⊥BC时
(2)如何翻折才能使折痕AD 与桌面垂直 为什么 折痕AD 与桌面垂直.
y
新知探究
直线与平面垂直的判定定理:
如果一条直线与一个平面内的两条相交直线垂直,那么该直线与此平面
反思 定理中的两条相交直线能否改成平行直线,
如果改成“无数条直线”呢
不能
垂 直.
符号语言:垂直
内
相交
图形语言:
→ l⊥α
线线垂直→线面垂直
lLa
l⊥b
a C α
bcα
a∩b=A
概念生成
例 3 求 证:如果两条平行直线中的一条直线垂直于一个平面,那么另一条直 线也垂直于这个平面.
已知:如 图 ,allb,a⊥a, 求 证 :b⊥a. 可作定理使用
证明:如图,在平面α内取两条相交直线m,n.
∵a⊥a,∴aLm,aLn.
又∵allb, ∴b⊥m,b⊥n.
又mca,nca, 且m,n是两条相交直线.
∴b⊥a.
结论:如果两条平行直线中的一条直线垂直于一个平 面,那么另一条直
线也垂直于这个平面. (证明线面垂直的另一方法)
典例分析
2. 如图,四棱锥 S-ABCD 的底面ABCD 是正方形, SD⊥平 面ABCD.
求证:AC⊥平 面SDB.
证 明 :∵SD⊥平面ABCD,ACc 平面ABCD.
∴SD⊥AC.
又∵底面ABCD是正方形,BD⊥AC,
而SDNBD=D
∴AC⊥平面SDB.
学以致用 教材P152
件时, A'C⊥B'D'
解:连接AC,BD, 当AC⊥BD时,A'C⊥B'D'.理由如下:
∵在直四棱柱A'B'C'D'-ABCD 中 ,AA'⊥底 面ABCD. BDC 底面ABCD,∴AA'⊥BD .
若AC⊥BD, 而AA'NAC=A.
则BD⊥平 面AA'C, 而A'C 平面AA'C,
∴则BD⊥A'C.
又∵ BB'//DD', 且BB'=DD',∴ 四边形BB'D'D 是平行四边形, ∴BD//B'D', 因此B'D'⊥A'C.
学以致用 教材P152
3. 如图,在直四棱柱A'B'C'D'-ABCD中,当底面四边形ABCD满足什么条
y 新知讲解
直线和平面所成角
1)斜线:和平面相交,但不垂直的直线叫做平面的斜线
2)斜足: 斜线和平面相交的交点
3)斜线在平面内的射影:
过斜线上斜足以外的一点向平面引垂线,
过垂足和斜足的直线称为斜线在平面内
的射影.
☆平面的斜线和它在平面内的射影所成的角,叫做直线和平面所成的角.
规定:①若直线垂直平面,则直线和平面所成的角为90°
( 2 ) 若 直 线 与 平 面平 行或 在 平 面 内. 则 直 线 和 平 面 所 成 的 角 为 0
☆直线和平面所成角的取值范围为
直线与平面所成的角是 直线与平面内任意一条 直线所成角的最小角.
P
学以致用 教材P152
1.如果两条直线和一个平面所成的角相等,那么这两条直线一定平行吗
不一定
典例分析
例6如图,正方体ABCD-A B C D 中,求:
(1A C 与 面ABCD 所成的角
(2)A B 与 面AB C D 所成的角
例 6 如图,正方体ABCD-A B C D 中,求:
(3)A C 与 面BB C C 所成的角
(4)A B 与 面A DCB 所成的角
(3)45° (4)30°
典例分析
例 6 ( 4 )A B 与面A DCB 所成的角
解 :连接BC 交B C 于点0,连接A O. 1.构造( 作 )
设正方体的棱长为a.
正方体ABCD-A B C D 中 ,A B ⊥ 平 面BCC B ,
∴A B ⊥BC , 又 B C⊥BC ,∴BC ⊥ 平 面A DCB . ∴A O 是A B 在平面A DCB 内的射影 .
∴∠BA O 为A B 和平面A DCB 所成的角。
: ·
在Rt△A BO 中 ,A B=√2a,
, ∠BA O=30°.
∴A B 和平面A DCB 所成的角为30° .
3.计算( 求 )
4.结论
典例分析
求直线和平面所成角的步骤
1.构造:作垂线 →作射影 →作平面角
2.证明: 证明某平面角就是斜线与平面所成角 (关键证垂直)
3.计算:求所成角,通常在垂线段、斜线和射影所构成的直角 三角形中计算.
4.下结论
方法归纳
4.过△ABC 所在平面α外一点P, 作PO⊥a, 垂足为0,连接PA,PB,PC.
(1)若PA=PB=PC, 则点0是△ABC的_外_ 心 .
(2)若PA=PB= PC,∠C=90°, 则点O是AB边的_中 _ 点 .
(3) 若PA⊥PB,PB⊥PC,PC⊥PA, 垂足都为P, 则点是△ABC的_垂_心。
学以致用 教材P152
(1)BC1 平 面PAB;(2)AE1 平面PBC;(3)PC1 平面AEF.
证明(1)∵ PA⊥ 平面ABC,BC c平面ABC,∴PA⊥BC. ∵∠ABC=90°,∴AB⊥BC.
又AB,PA c平面PAB,AB∩PA=A,
∴BC⊥ 平 面PAB.
(2):BC⊥ 平面PAB,AE c平面PAB, ∴BC⊥AE. ∵PB⊥AE,BC∩PB=B,BC,PB c平面PBC,
∴AE⊥平面PBC.
(3):AE1 平面PBC,PCc 平面PBC,∴AE⊥PC. ∵AF⊥PC,AE∩AF=A,AE,AF c平面AEF, ∴PC1平面AEF.
y 能力提升
1 . 如图,P 为△ABC 所在平面外一点,PA1 平面ABC,∠ABC=90°,AE⊥PB 于点E,AF⊥PC 于点F, 求证:
直线与平面垂直
题型一
例题
例 题 2.如图,在棱长为2的正方体ABCD-A B C D 中 , 点E是 D C 的 中 点 ,F 是 侧
面 ADD A 的中心,则点F到 平 面EB C 的距离为( A
B. C. D.√3
[解析]连接A D,DE,DB , 因为F是侧面ADD A 的中心,所以F∈A D,
因为 ,所以四边形A B CD 是平行四边形,所以A D//CB ,
因为A D 女平面EB C,CB c 平面EB C, 所 以A D// 平面EB C, 所以点F到平面EB C 的距离与点D到平面EB C 的距离相等,
设点D到平面EB C的距离为h, 在△EB C中 ,EB =CE=√5,B C=2√2,
所以S
y 能力提升
.所以点F到平面EB C 的距离为
题 型 二
点到平面的距离
例题 3.如果P是等边△ABC 所在平面外一点,且 △ABC的 边
长为1,那么PA与底面ABC所成的角是( A )
A. 30° B. 45° C.60° D. 90°
y
[解析] 如图,作PO1 平面ABC 于点0,连接AO,
易知P-ABC 为正三棱锥,PA 与底面ABC 所成的角即为∠PAO,
直线与平面所成的角
能力提升
,故∠PAO=30° .
题型三
故选A.
(1)利用定义; 垂直于平面内任意一条直线
(2)利用判定定理.线线垂直 > 线面垂直
4. 数学思想方法:转化的思想
空间问题 > 平面问题
1. 直线与平面垂直的定义
定义的运用:线面垂直 > 线线垂直
l⊥α,acα=l⊥a
2.直线与平面所成角的概念及范围
3. 直线与平面垂直的判定
y 课堂小结
范 围 :
人教A 版2019必修第二册
感谢聆听
主 讲 :
第八章立体几何初步
人教A版2019必修第二册
8.6.2 直线与平面垂直(第1课时)
理解直线与平面垂直的判定定理,并会对其进行简单的应 用,培养直观想象、逻辑推理的核心素养
理解直线与平面所成的角的概念,并能解决简单的线面角 问题,培养数学运算的核心素养
会求点到平面的距离,培养数学运算的核心素养.
学习目标
1
a//a
直线与平面平行
aNa=A
直线与平面相交
垂直 斜交
aCa
a a 直线在平面内
a
空间中直线与平面有几种位置关系
直线在平面外
afα
y 复习回顾
线面位 置关系
a
b
a
a
观察1 在日常生活中,我们对直线与平面垂直有很多感性认识.比如,旗 杆与底面的位置关系,教室里相邻墙面的交线与地面的位置关系,都给我 们以直线与平面垂直的形象.
y 新课导入
观察2 如图示,在阳光下观察直立于
底面的旗杆AB及它在地面的影子BC.
随着时间的变化,影子BC 的位置在不
断地变化,旗杆所在直线AB 与其影子
BC 所在直线是否保持垂直
直线AB与其影子BC所在直线始终保持垂直.
旗杆AB 所在直线于地面上任意一条过点B 的直线垂直.
追 问 旗 杆AB 与地面上任意一条不过旗
杆底部B的直线的位置关系又是什么
与地面内任意一条不过
点B的直线B'D'也垂直. B'
y
直线AB垂直 于平面内的任 意一条直线。
新课导入
C'
直线与平面垂直的定义
一般地,如果直线与平面α内的任意一条直线都垂直,我们就说直线与
平面α互相垂直,记作l⊥a.直线l叫做平面α的垂线,平面α叫做直线l的垂面. 直线与平面垂直时,它们唯一的公共点P叫做垂足.
平面α的垂线
l
垂足 直线l的垂面
P
a
y
画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.
概念生成
反思:“若lLa, 则直线l与平面α内任意一条直线都垂直”,对吗
|L
lLα l⊥a
a lP aCC
a
线面垂直 线线垂直
线面垂直的最基本的性质。
y
新知探究
问题1在同一平面内,过一点有且只有一条直线与已知直线垂直,将这一结 论推广到空间,过一点垂直于已知平面的直线有几条 为什么
过一点垂直于已知平面的直线有且只有一条.
证 明 :
如图,若过平面α外一点可以作平面的两条垂线a,b,
则两相交直线 a,b 确定一个平面,设为β,
设α∩β=l, 因为a⊥a,b⊥a, 所 以a⊥l,b⊥l,
又 acβ,bcβ, 所以 a//b,
与 a∩b=P 相矛盾,所以过平面外 一点作平面的垂线
有且只有一条
y
新知探究
点到平面的距离
过一点作垂直于已知平面的直线,则该点与垂足间的线段,叫做这个点 到该平面的垂线段,垂线段的长度叫做这个点到该平面的距离.
h=|AB|
在锥体的体积公式中,锥体的高度就是锥体的顶点到底面的距离.
下面我们研究直线与平面垂直的判定,就是直线与平面垂直的充分条件 .
y
概念生成
问题2 怎么来判定直线与平面垂直 由定义判定直线与平面垂直,简便吗
能否只需验证直线与平面内部分直线垂直就能判定直线与平面垂直呢
探究准备一块三角形的纸片ABC, 过△ABC 的顶点A翻折纸片,得到折痕
AD, 将翻折后的纸片竖起放置在桌面上(BD,DC 与桌面接触).观察:
(1)折痕AD 与桌面垂直吗 不一定 当AD⊥BC时
(2)如何翻折才能使折痕AD 与桌面垂直 为什么 折痕AD 与桌面垂直.
y
新知探究
直线与平面垂直的判定定理:
如果一条直线与一个平面内的两条相交直线垂直,那么该直线与此平面
反思 定理中的两条相交直线能否改成平行直线,
如果改成“无数条直线”呢
不能
垂 直.
符号语言:垂直
内
相交
图形语言:
→ l⊥α
线线垂直→线面垂直
lLa
l⊥b
a C α
bcα
a∩b=A
概念生成
例 3 求 证:如果两条平行直线中的一条直线垂直于一个平面,那么另一条直 线也垂直于这个平面.
已知:如 图 ,allb,a⊥a, 求 证 :b⊥a. 可作定理使用
证明:如图,在平面α内取两条相交直线m,n.
∵a⊥a,∴aLm,aLn.
又∵allb, ∴b⊥m,b⊥n.
又mca,nca, 且m,n是两条相交直线.
∴b⊥a.
结论:如果两条平行直线中的一条直线垂直于一个平 面,那么另一条直
线也垂直于这个平面. (证明线面垂直的另一方法)
典例分析
2. 如图,四棱锥 S-ABCD 的底面ABCD 是正方形, SD⊥平 面ABCD.
求证:AC⊥平 面SDB.
证 明 :∵SD⊥平面ABCD,ACc 平面ABCD.
∴SD⊥AC.
又∵底面ABCD是正方形,BD⊥AC,
而SDNBD=D
∴AC⊥平面SDB.
学以致用 教材P152
件时, A'C⊥B'D'
解:连接AC,BD, 当AC⊥BD时,A'C⊥B'D'.理由如下:
∵在直四棱柱A'B'C'D'-ABCD 中 ,AA'⊥底 面ABCD. BDC 底面ABCD,∴AA'⊥BD .
若AC⊥BD, 而AA'NAC=A.
则BD⊥平 面AA'C, 而A'C 平面AA'C,
∴则BD⊥A'C.
又∵ BB'//DD', 且BB'=DD',∴ 四边形BB'D'D 是平行四边形, ∴BD//B'D', 因此B'D'⊥A'C.
学以致用 教材P152
3. 如图,在直四棱柱A'B'C'D'-ABCD中,当底面四边形ABCD满足什么条
y 新知讲解
直线和平面所成角
1)斜线:和平面相交,但不垂直的直线叫做平面的斜线
2)斜足: 斜线和平面相交的交点
3)斜线在平面内的射影:
过斜线上斜足以外的一点向平面引垂线,
过垂足和斜足的直线称为斜线在平面内
的射影.
☆平面的斜线和它在平面内的射影所成的角,叫做直线和平面所成的角.
规定:①若直线垂直平面,则直线和平面所成的角为90°
( 2 ) 若 直 线 与 平 面平 行或 在 平 面 内. 则 直 线 和 平 面 所 成 的 角 为 0
☆直线和平面所成角的取值范围为
直线与平面所成的角是 直线与平面内任意一条 直线所成角的最小角.
P
学以致用 教材P152
1.如果两条直线和一个平面所成的角相等,那么这两条直线一定平行吗
不一定
典例分析
例6如图,正方体ABCD-A B C D 中,求:
(1A C 与 面ABCD 所成的角
(2)A B 与 面AB C D 所成的角
例 6 如图,正方体ABCD-A B C D 中,求:
(3)A C 与 面BB C C 所成的角
(4)A B 与 面A DCB 所成的角
(3)45° (4)30°
典例分析
例 6 ( 4 )A B 与面A DCB 所成的角
解 :连接BC 交B C 于点0,连接A O. 1.构造( 作 )
设正方体的棱长为a.
正方体ABCD-A B C D 中 ,A B ⊥ 平 面BCC B ,
∴A B ⊥BC , 又 B C⊥BC ,∴BC ⊥ 平 面A DCB . ∴A O 是A B 在平面A DCB 内的射影 .
∴∠BA O 为A B 和平面A DCB 所成的角。
: ·
在Rt△A BO 中 ,A B=√2a,
, ∠BA O=30°.
∴A B 和平面A DCB 所成的角为30° .
3.计算( 求 )
4.结论
典例分析
求直线和平面所成角的步骤
1.构造:作垂线 →作射影 →作平面角
2.证明: 证明某平面角就是斜线与平面所成角 (关键证垂直)
3.计算:求所成角,通常在垂线段、斜线和射影所构成的直角 三角形中计算.
4.下结论
方法归纳
4.过△ABC 所在平面α外一点P, 作PO⊥a, 垂足为0,连接PA,PB,PC.
(1)若PA=PB=PC, 则点0是△ABC的_外_ 心 .
(2)若PA=PB= PC,∠C=90°, 则点O是AB边的_中 _ 点 .
(3) 若PA⊥PB,PB⊥PC,PC⊥PA, 垂足都为P, 则点是△ABC的_垂_心。
学以致用 教材P152
(1)BC1 平 面PAB;(2)AE1 平面PBC;(3)PC1 平面AEF.
证明(1)∵ PA⊥ 平面ABC,BC c平面ABC,∴PA⊥BC. ∵∠ABC=90°,∴AB⊥BC.
又AB,PA c平面PAB,AB∩PA=A,
∴BC⊥ 平 面PAB.
(2):BC⊥ 平面PAB,AE c平面PAB, ∴BC⊥AE. ∵PB⊥AE,BC∩PB=B,BC,PB c平面PBC,
∴AE⊥平面PBC.
(3):AE1 平面PBC,PCc 平面PBC,∴AE⊥PC. ∵AF⊥PC,AE∩AF=A,AE,AF c平面AEF, ∴PC1平面AEF.
y 能力提升
1 . 如图,P 为△ABC 所在平面外一点,PA1 平面ABC,∠ABC=90°,AE⊥PB 于点E,AF⊥PC 于点F, 求证:
直线与平面垂直
题型一
例题
例 题 2.如图,在棱长为2的正方体ABCD-A B C D 中 , 点E是 D C 的 中 点 ,F 是 侧
面 ADD A 的中心,则点F到 平 面EB C 的距离为( A
B. C. D.√3
[解析]连接A D,DE,DB , 因为F是侧面ADD A 的中心,所以F∈A D,
因为 ,所以四边形A B CD 是平行四边形,所以A D//CB ,
因为A D 女平面EB C,CB c 平面EB C, 所 以A D// 平面EB C, 所以点F到平面EB C 的距离与点D到平面EB C 的距离相等,
设点D到平面EB C的距离为h, 在△EB C中 ,EB =CE=√5,B C=2√2,
所以S
y 能力提升
.所以点F到平面EB C 的距离为
题 型 二
点到平面的距离
例题 3.如果P是等边△ABC 所在平面外一点,且 △ABC的 边
长为1,那么PA与底面ABC所成的角是( A )
A. 30° B. 45° C.60° D. 90°
y
[解析] 如图,作PO1 平面ABC 于点0,连接AO,
易知P-ABC 为正三棱锥,PA 与底面ABC 所成的角即为∠PAO,
直线与平面所成的角
能力提升
,故∠PAO=30° .
题型三
故选A.
(1)利用定义; 垂直于平面内任意一条直线
(2)利用判定定理.线线垂直 > 线面垂直
4. 数学思想方法:转化的思想
空间问题 > 平面问题
1. 直线与平面垂直的定义
定义的运用:线面垂直 > 线线垂直
l⊥α,acα=l⊥a
2.直线与平面所成角的概念及范围
3. 直线与平面垂直的判定
y 课堂小结
范 围 :
人教A 版2019必修第二册
感谢聆听
主 讲 :
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
