2024-2025学年北师大版数学七年级下册 5.2 课时2 线段的垂直平分线 学案(含答案)
文档属性
| 名称 | 2024-2025学年北师大版数学七年级下册 5.2 课时2 线段的垂直平分线 学案(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 184.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-22 00:00:00 | ||
图片预览

文档简介
5.2 课时2 线段的垂直平分线 学案
一、学习目标
1.知道线段垂直平分线的定义.
2.知道并掌握线段垂直平分线性质,能利用线段垂直平分线的性质解决实际问题.
3.能利用尺规作图画出线段的垂直平分线.
二、自主预习
1.什么是轴对称图形 它的对称轴是什么
2.下面哪些图形是轴对称图形
三、课堂练习
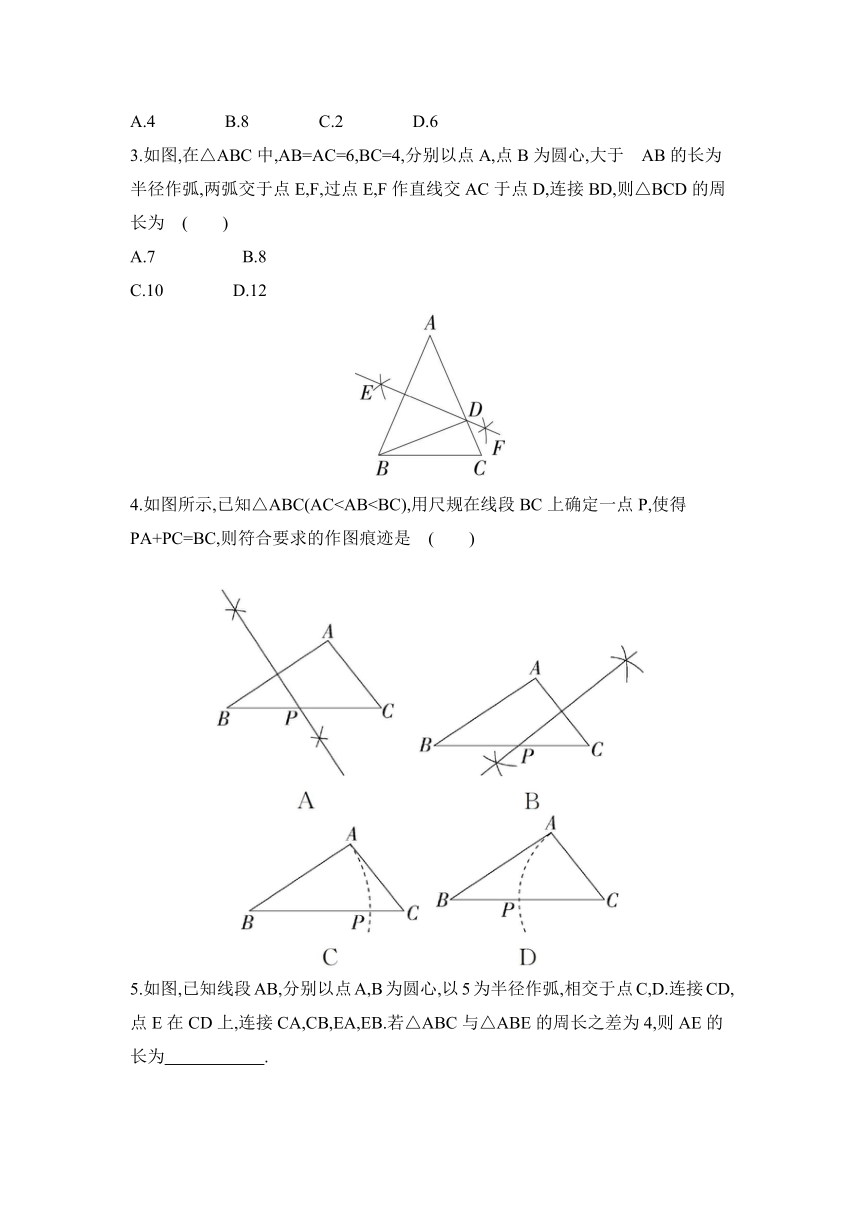
1.如图,在Rt△ABC中,∠ACB=90°,DE垂直平分AB交BC于点D,若△ACD的周长为50 cm,则AC+BC= ( )
A.25 cm B.45 cm
C.50 cm D.55 cm
2.如图,在△ABC中,点O是△ABC内一点,连接OB、OC,OD垂直平分AB,若OB=OC,OC=4,则点A,O之间的距离为 ( )
A.4 B.8 C.2 D.6
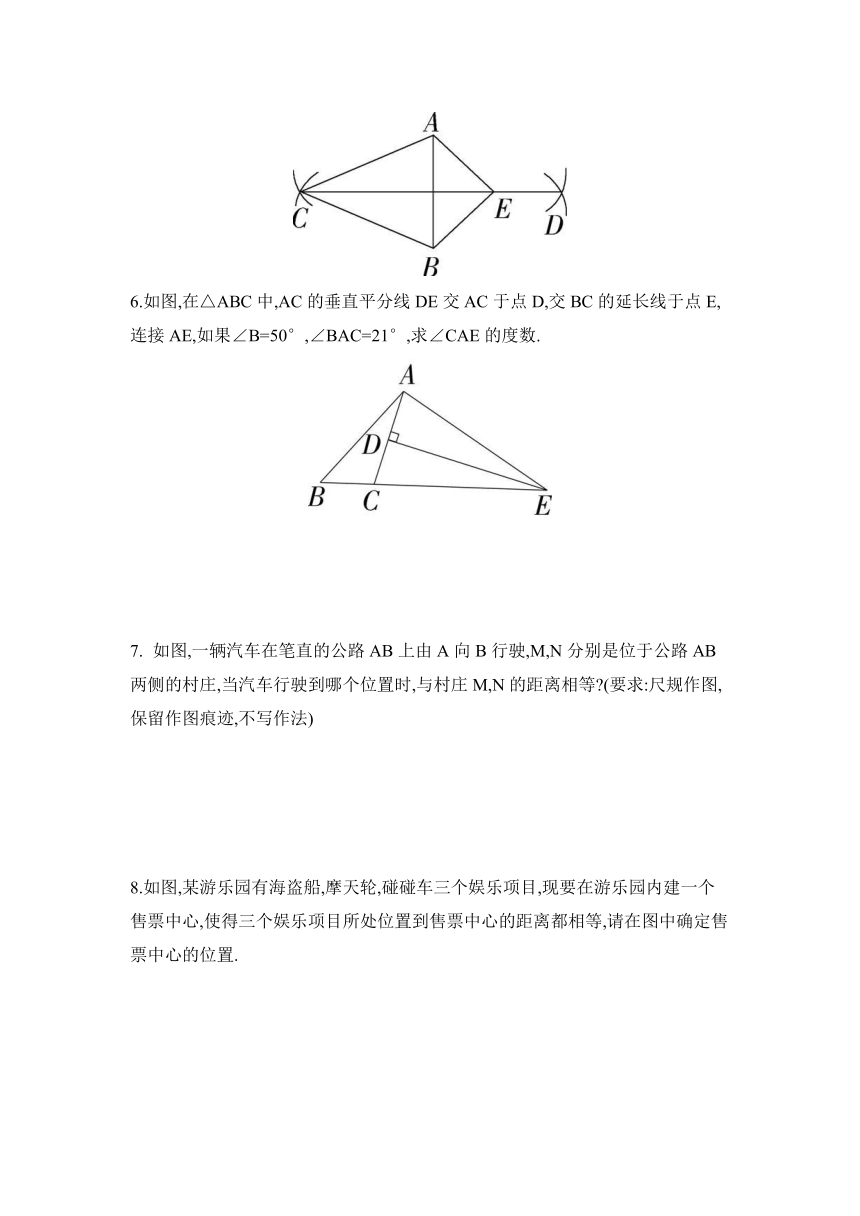
3.如图,在△ABC中,AB=AC=6,BC=4,分别以点A,点B为圆心,大于 AB的长为半径作弧,两弧交于点E,F,过点E,F作直线交AC于点D,连接BD,则△BCD的周长为 ( )
A.7 B.8
C.10 D.12
4.如图所示,已知△ABC(AC5.如图,已知线段AB,分别以点A,B为圆心,以5为半径作弧,相交于点C,D.连接CD,点E在CD上,连接CA,CB,EA,EB.若△ABC与△ABE的周长之差为4,则AE的长为 .
6.如图,在△ABC中,AC的垂直平分线DE交AC于点D,交BC的延长线于点E,连接AE,如果∠B=50°,∠BAC=21°,求∠CAE的度数.
如图,一辆汽车在笔直的公路AB上由A向B行驶,M,N分别是位于公路AB两侧的村庄,当汽车行驶到哪个位置时,与村庄M,N的距离相等 (要求:尺规作图,保留作图痕迹,不写作法)
8.如图,某游乐园有海盗船,摩天轮,碰碰车三个娱乐项目,现要在游乐园内建一个售票中心,使得三个娱乐项目所处位置到售票中心的距离都相等,请在图中确定售票中心的位置.
参考答案
二、自主预习
1.如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫作轴对称图形,这条直线叫作对称轴.
2.第一个和第三个图形是轴对称图形.
三、课堂练习
1.【解析】 因为DE垂直平分AB交BC于点D,所以AD=DB.
因为△ACD的周长为50 cm,
所以AC+CD+AD=AC+CD+DB=AC+BC=50 cm,故选C.
2.【解析】 如图,连接OA.
因为OD垂直平分AB,所以OA=OB.
因为OB=OC=4,所以OA=OB=OC=4,故选A.
3.【解析】由题图知,EF垂直平分AB,所以AD=BD.
所以△BCD的周长=BD+CD+BC=AD+CD+BC=AC+BC.因为
AB=AC=6,BC=4,所以△BCD的周长=6+4=10.故选C.
4.【解析】因为PA+PC=BC,点P在线段BC上,
所以PA=BC-PC=PB,
所以点P在线段AB的垂直平分线上,
结合选项可知,选A.
5.【解析】由作图可知,直线CD是线段AB的垂直平分线,所以CA
=CB=5,EA=EB,
因为△ABC与△ABE的周长之差为4,
所以(CA+CB+AB)-(EA+EB+AB)=4,
所以2CA-2AE=4,
所以AC-AE=2,
因为AC=5,所以AE=3.
6.【解析】因为DE垂直平分AC,所以EA=EC.
所以∠EAC=∠ECA.因为∠B=50°,∠BAC=21°,所以∠BCA=
180°-∠B-∠BAC=109°,所以∠CAE=∠ECA=180°-∠BCA=
180°-109°=71°.
7.【解析】如图,C点即为所求.
8.【解析】 如图,连接AB,AC,分别作线段AB,AC的垂直平分线,两
条垂直平分线相交于点P,则点P就是售票中心的位置.
一、学习目标
1.知道线段垂直平分线的定义.
2.知道并掌握线段垂直平分线性质,能利用线段垂直平分线的性质解决实际问题.
3.能利用尺规作图画出线段的垂直平分线.
二、自主预习
1.什么是轴对称图形 它的对称轴是什么
2.下面哪些图形是轴对称图形
三、课堂练习
1.如图,在Rt△ABC中,∠ACB=90°,DE垂直平分AB交BC于点D,若△ACD的周长为50 cm,则AC+BC= ( )
A.25 cm B.45 cm
C.50 cm D.55 cm
2.如图,在△ABC中,点O是△ABC内一点,连接OB、OC,OD垂直平分AB,若OB=OC,OC=4,则点A,O之间的距离为 ( )
A.4 B.8 C.2 D.6
3.如图,在△ABC中,AB=AC=6,BC=4,分别以点A,点B为圆心,大于 AB的长为半径作弧,两弧交于点E,F,过点E,F作直线交AC于点D,连接BD,则△BCD的周长为 ( )
A.7 B.8
C.10 D.12
4.如图所示,已知△ABC(AC
6.如图,在△ABC中,AC的垂直平分线DE交AC于点D,交BC的延长线于点E,连接AE,如果∠B=50°,∠BAC=21°,求∠CAE的度数.
如图,一辆汽车在笔直的公路AB上由A向B行驶,M,N分别是位于公路AB两侧的村庄,当汽车行驶到哪个位置时,与村庄M,N的距离相等 (要求:尺规作图,保留作图痕迹,不写作法)
8.如图,某游乐园有海盗船,摩天轮,碰碰车三个娱乐项目,现要在游乐园内建一个售票中心,使得三个娱乐项目所处位置到售票中心的距离都相等,请在图中确定售票中心的位置.
参考答案
二、自主预习
1.如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫作轴对称图形,这条直线叫作对称轴.
2.第一个和第三个图形是轴对称图形.
三、课堂练习
1.【解析】 因为DE垂直平分AB交BC于点D,所以AD=DB.
因为△ACD的周长为50 cm,
所以AC+CD+AD=AC+CD+DB=AC+BC=50 cm,故选C.
2.【解析】 如图,连接OA.
因为OD垂直平分AB,所以OA=OB.
因为OB=OC=4,所以OA=OB=OC=4,故选A.
3.【解析】由题图知,EF垂直平分AB,所以AD=BD.
所以△BCD的周长=BD+CD+BC=AD+CD+BC=AC+BC.因为
AB=AC=6,BC=4,所以△BCD的周长=6+4=10.故选C.
4.【解析】因为PA+PC=BC,点P在线段BC上,
所以PA=BC-PC=PB,
所以点P在线段AB的垂直平分线上,
结合选项可知,选A.
5.【解析】由作图可知,直线CD是线段AB的垂直平分线,所以CA
=CB=5,EA=EB,
因为△ABC与△ABE的周长之差为4,
所以(CA+CB+AB)-(EA+EB+AB)=4,
所以2CA-2AE=4,
所以AC-AE=2,
因为AC=5,所以AE=3.
6.【解析】因为DE垂直平分AC,所以EA=EC.
所以∠EAC=∠ECA.因为∠B=50°,∠BAC=21°,所以∠BCA=
180°-∠B-∠BAC=109°,所以∠CAE=∠ECA=180°-∠BCA=
180°-109°=71°.
7.【解析】如图,C点即为所求.
8.【解析】 如图,连接AB,AC,分别作线段AB,AC的垂直平分线,两
条垂直平分线相交于点P,则点P就是售票中心的位置.
同课章节目录
