2025年甘肃省武威第二十中学中考数学 锐角三角函数 专项练习题(含答案)
文档属性
| 名称 | 2025年甘肃省武威第二十中学中考数学 锐角三角函数 专项练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-22 17:15:39 | ||
图片预览


文档简介
2025年甘肃省武威第二十中学中考数学人教版《锐角三角函数》专项练习题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
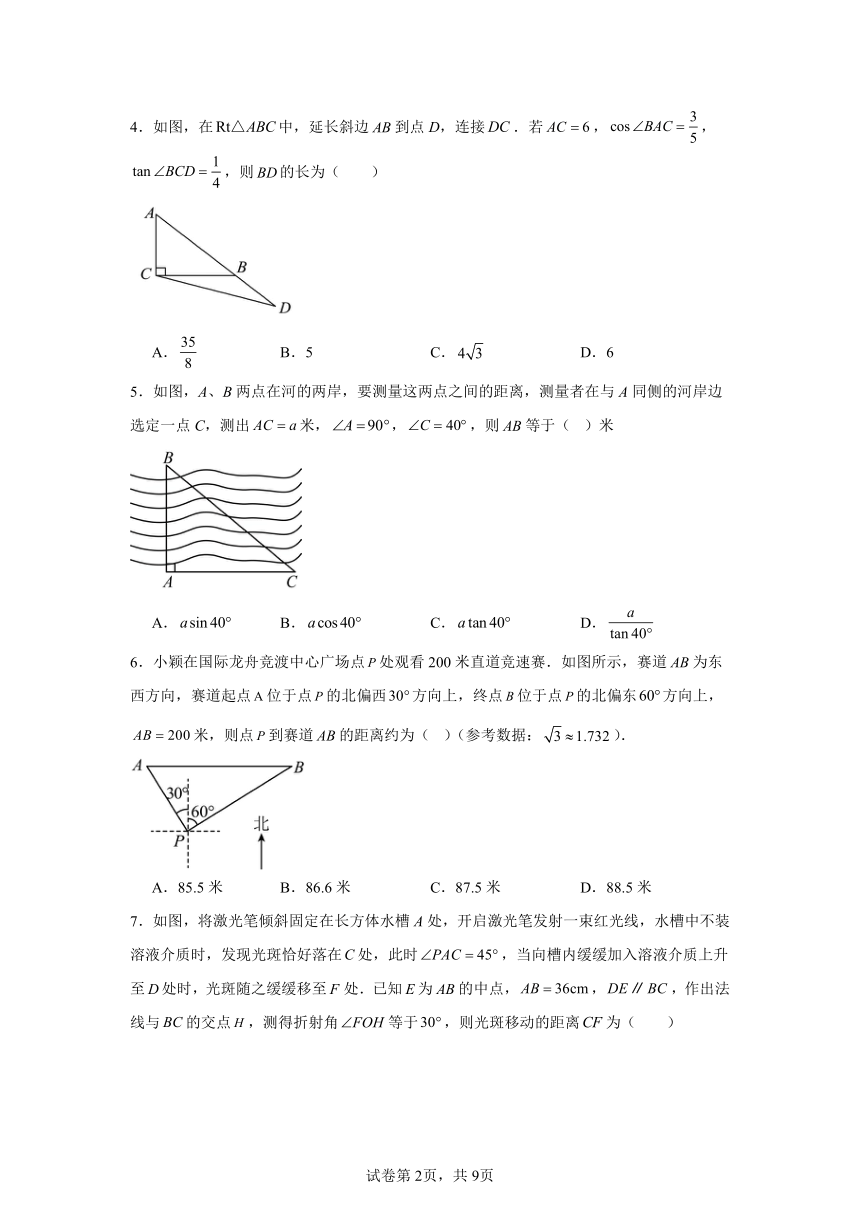
1.如图,在中,于点D,,则的度数为( )
A. B. C. D.
2.如图,正方形中,将边绕点逆时针旋转至,连接,,若,则的值是( )
A. B. C. D.
3.如图,是等腰直角三角形,,为延长线上一点,为上一点,连接交于点,作交直线于点,若,,,则( )
A. B.3 C. D.
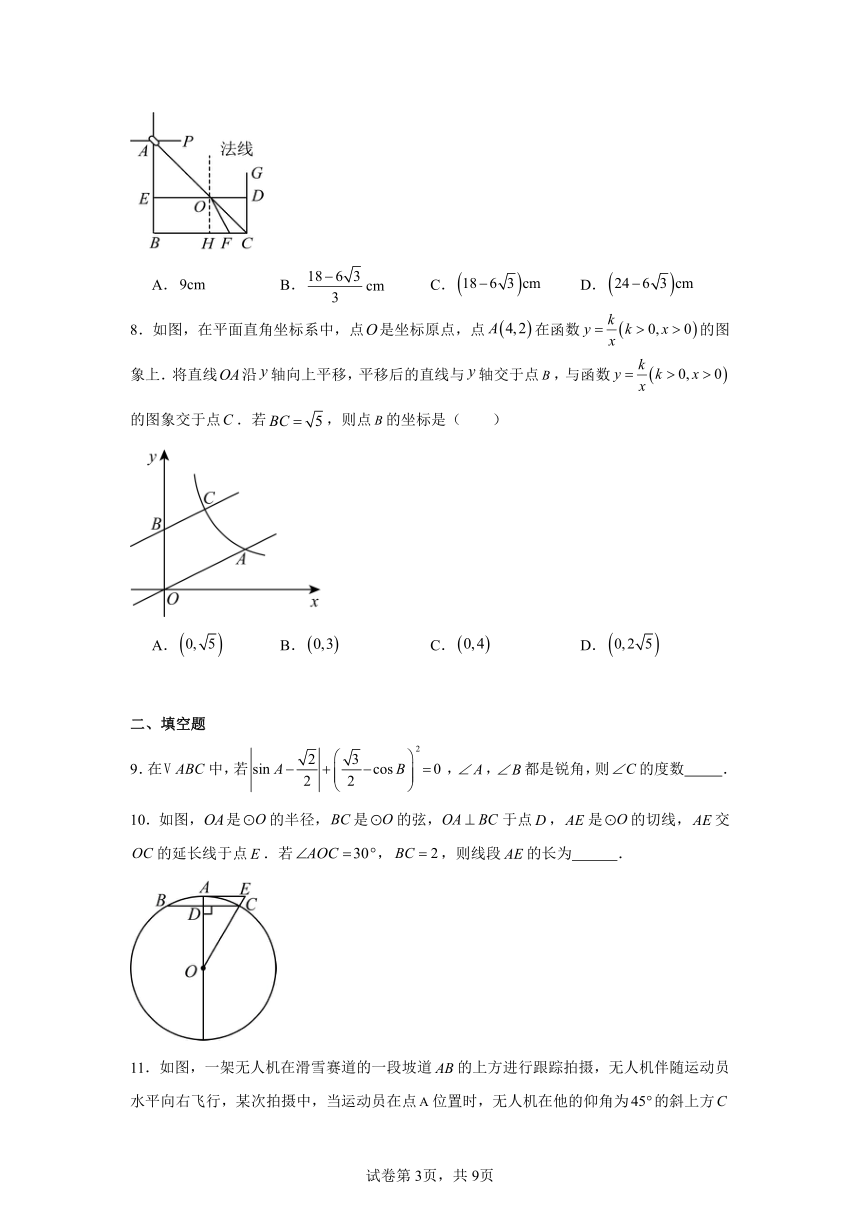
4.如图,在中,延长斜边到点D,连接.若,,,则的长为( )
A. B.5 C. D.6
5.如图,A、B两点在河的两岸,要测量这两点之间的距离,测量者在与A同侧的河岸边选定一点C,测出米,,,则等于( )米
A. B. C. D.
6.小颖在国际龙舟竞渡中心广场点处观看200米直道竞速赛.如图所示,赛道为东西方向,赛道起点位于点的北偏西方向上,终点位于点的北偏东方向上,米,则点到赛道的距离约为( )(参考数据:).
A.85.5米 B.86.6米 C.87.5米 D.88.5米
7.如图,将激光笔倾斜固定在长方体水槽A处,开启激光笔发射一束红光线,水槽中不装溶液介质时,发现光斑恰好落在处,此时,当向槽内缓缓加入溶液介质上升至处时,光斑随之缓缓移至处.已知为的中点,,,作出法线与的交点,测得折射角等于,则光斑移动的距离为( )
A. B. C. D.
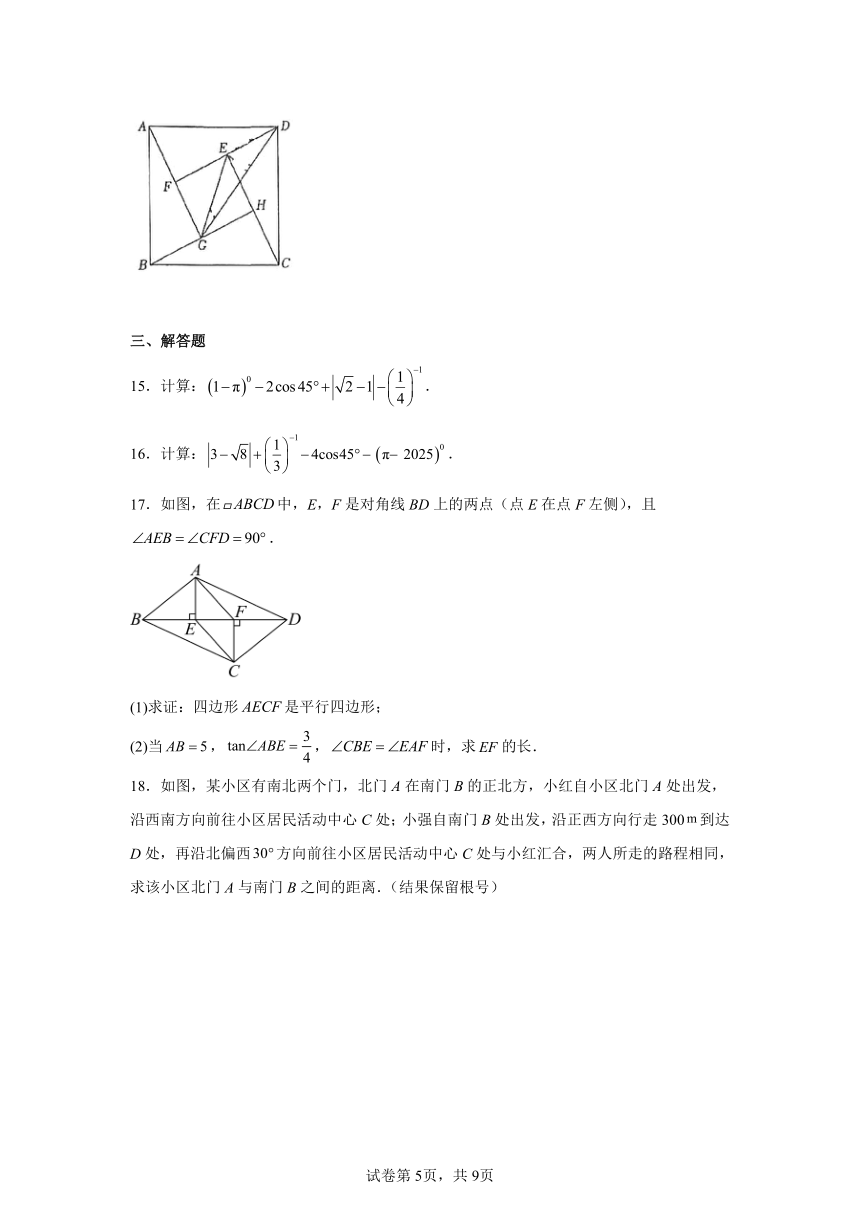
8.如图,在平面直角坐标系中,点是坐标原点,点在函数的图象上.将直线沿轴向上平移,平移后的直线与轴交于点,与函数的图象交于点.若,则点的坐标是( )
A. B. C. D.
二、填空题
9.在中,若,,都是锐角,则的度数 .
10.如图,是的半径,是的弦,于点,是的切线,交的延长线于点.若,,则线段的长为 .
11.如图,一架无人机在滑雪赛道的一段坡道的上方进行跟踪拍摄,无人机伴随运动员水平向右飞行,某次拍摄中,当运动员在点位置时,无人机在他的仰角为的斜上方处,当运动员到达地面点时,无人机恰好到达运动员正上方的处,已知的坡度为且长为300米,无人机飞行距离为60米,则无人机离地面高度的长是 米.(参考数据:)
12.如图是水槽水龙头的侧面图,矩形为水槽侧面,宽,深,排水口位于的中点.在水槽边正上方安装水管,水龙头.按水龙头安装要求,水流需直接对准排水口确保水快速排入管道.测得,,则安装的水管的长为 .(精确到,参考数据:,,,)
13.如图,是的弦,半径于点D,连结.若的半径长为,的长为,则扇形的面积是 (结果保留).
14.勾股定理的证明方法丰富多样,其中我国古代数学家赵爽利用“弦图”的证明简明、直观,是世界公认最巧妙的方法.“赵爽弦图”已成为我国古代数学成就的一个重要标志,千百年来倍受人们的喜爱,小亮在如图所示的“赵爽弦图”中,连接,.若正方形与的边长之比为,则等于 .
三、解答题
15.计算:.
16.计算:.
17.如图,在中,E,F是对角线BD上的两点(点E在点F左侧),且.
(1)求证:四边形是平行四边形;
(2)当,,时,求的长.
18.如图,某小区有南北两个门,北门A在南门B的正北方,小红自小区北门A处出发,沿西南方向前往小区居民活动中心C处;小强自南门B处出发,沿正西方向行走300到达D处,再沿北偏西方向前往小区居民活动中心C处与小红汇合,两人所走的路程相同,求该小区北门A与南门B之间的距离.(结果保留根号)
19.如图,已知是的直径,为的内接三角形,为延长线上一点,连接于点,交于点.
(1)求证:是的切线.
(2)若,求的长.
20.如图所示,在中,,弦与弦交于点,弦与交于点,连接.
(1)求证:;
(2)若的直径长为,,求图中阴影部分面积.
21.如图,内接于,为的直径,延长至点D,使得.
(1)求证:是的切线;
(2)若,,求的长.
22.广州地铁经过多年的发展,地铁出入口更加人性化和便民化.如图1是某地铁出入口,有步梯和电梯两种由地下层通往地面层的出入方式.其截面如图2所示,是由地下直通地面的电梯,,,,,是步梯,,,的倾角相同,,与地面平行.已知电梯全长30米,倾角为,米.
(1)求地面层与地下层的垂直高度;
(2)求步梯的倾角的正切值和步梯通道的全长.参考数据:,,.
23.如图,⊙是的外接圆,是直径,,延长到点,使得,半径与交于点,连接与交于点.
(1)求证:是⊙的切线;
(2)若,求的长度;
(3)若是的中点,如图,求.
24.在平面直角坐标系中,抛物线经过点抛物线上点,的坐标分别为,.
(1)求抛物线的表达式;
(2)当时,求的取值范围;
(3)过点作轴的垂线,过点作轴的垂线,直线,交点为,以,为边作矩形.
①求;
②线段与轴相交于点,以为边作矩形,使矩形在轴同侧,且.当矩形与矩形重合部分图形的面积是矩形面积的时,求的值.
25.综合与实践:
主题:光的折射规律.
【实验操作】
第一步:将长方体空水槽放置在水平桌面上,束光线从林槽边沿A处投射到底部B处,入射光线与水槽内壁AC的夹角为;
第二步:向水槽注水,水面上升到的中点处时,停止注水.(直线为法线,为入射光线,为折射光线.)
【测量数据】
如图,点,,,,,,,,在同一平面内,测得,,折射角.
【问题解决】
根据以上实验操作和测量的数据,解答下列问题:
(1)求的长;
(2)求,之间的距离(结果精确到0.1cm):
(参考数据:,,)
26.如图,在平面直角坐标系中,正方形的边在轴的正半轴上,顶点,在第一象限内,正比例函数的图象经过点,反比例函数的图象经过点,且与边交于点,连接,已知.
(1)求的值;
(2)观察图象,请直接写出满足的的取值范围;
(3)连接,在线段上取一点,使,过点P作垂直轴,交双曲线于点,请求出线段的长.
试卷第1页,共3页
试卷第1页,共3页
《2025年甘肃省武威第二十中学中考数学人教版《锐角三角函数》专项练习题》参考答案
题号 1 2 3 4 5 6 7 8
答案 B C D B C B C B
9./度
10./
11.345
12.
13.
14.
15.解:
16.解:
.
17.(1)证明:,
,,
,
四边形是平行四边形,
,,
,
在和中,
,
,
,
四边形是平行四边形;
(2)解:在中,,
设,则,
由勾股定理得:,
解得:或(舍去),
,,
由(1)得:四边形是平行四边形,
,,
,
,
,
,
,
设,则,
,
解得:或,(舍去),
即.
18.解:过点C作于M,过D作于N,
又∵,
∴四边形是矩形,
∴,;
设,则;
∵,
∴,,
∴;
∵,
∴,,
∵两人所走的路程相同,
∴,即,
解得:;
∵,
∴
即小区北门A与南门B之间的距离为.
19.(1)证明:如图,连接,
,
,
,
,
∴
是的半径,
是的切线;.
(2)解:在中,,
,
是等边三角形,
,
是直径,
,
在中,.
20.(1)证明: ,
,又,
,
,即;
(2)解:连接,,过作,垂足为点,如图所示:
,
,
又,
,
在中,,
,
,
,
则.
21.(1)证明:连接,则:,
∴,
∵,
∴,
∵为的直径,
∴,
∴,
∴,即:,
∴,
又∵是的半径,
∴是的切线;
(2)∵,
∴,
在中,,
∴,
∵,,
∴△DCA∽△DBC
∴,
∴,
∴,即:,
解得:或(舍去);
∴.
22.(1)解:根据题意,得(米),
答:地面层与地下层的垂直高度约为18米.
(2)解:延长交于点M,延长交于点N,
∵,,的倾角相同,,与地面平行.
∴,
∴,
∵,
∴四边形,四边形都是平行四边形,
∴,
∵电梯全长30米,倾角为,米.
∴(米),
(米),
(米),
∴(米),
∴,
∴,
∴,
∴(米),
∴步梯通道的全长为(米).
23.(1)证明:是的直径,
,
,
,
,
即,
是的直径,
是的切线;
(2)解:,
,,
又,
,
,
,
,
;
(3)解:为直径,,
,
,
,
、,
,
、,
又,
是的中位线,
设,则,
,
,
解得:,
则、,
,
,
,
则.
24.(1)解:∵抛物线经过点,
∴,
∴,
∴抛物线的表达式为;
(2)解:当时,,
解得,,
∴抛物线与轴的交点坐标为和,
∴当时,;
当或时,;
①∵,,,
∴当时,,此时,
∴,
∵,
∴点在第四象限,即,
∴,
∴;
②当时,,
当点在第三象限,,
∴,
∴此时点在第四象限,即,
∴,不符合题意,舍去;
当点在第四象限,,
∴,
∵,
∴点在第一象限,即,
解得,
∴;
综上,或;
(3)解:①∵点,在抛物线上,
∴,,
如图,当点在第一象限,点在第四象限时,
,,
∴;
如图,当点在第四象限,点在第一象限时,
,,
∴;
②中,,
设,,
∴,
∴,
如图,当点在第一象限,点在第四象限时,
,
∵轴,
∴,
∴,
∴,
∵四边形为矩形,
∴,
∴,
∴,
∵,
∴,
∴,
∵,,
∴,
∴,
∴,
∴,
解得,(舍去);
如图,当点在第四象限,点在第一象限时,
同理可知,
此时,
∴,
解得(舍去),.
综上,m的值为或.
25.(1)解:在中,,
,
;
(2)解:由题可知,,
,
,
,
又,
,
.
26.(1)解:∵四边形是正方形,
∴,
在函数中,当时,,
∴点D的坐标为,
∵点D的坐标为且在反比例函数图象上,
∴,
∴,
∵正方形的边长为3,
∴,
把代入函数中,得,
∴,
∴,
∴;
(2)解:∵在函数中,当时,,
∴由图象可知的x的取值范围为;
(3)解:设直线的解析式为,代入点和得:
,
解得,
∴直线的解析式为,
过点作,交于点,
则,
∴,
∴,
∴,
∵,
∴设直线的解析式为:,把代入得:,
∴直线的解析式为,
∴当时,,
∴,
在反比例函数中,当时,,
∴,
∴.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在中,于点D,,则的度数为( )
A. B. C. D.
2.如图,正方形中,将边绕点逆时针旋转至,连接,,若,则的值是( )
A. B. C. D.
3.如图,是等腰直角三角形,,为延长线上一点,为上一点,连接交于点,作交直线于点,若,,,则( )
A. B.3 C. D.
4.如图,在中,延长斜边到点D,连接.若,,,则的长为( )
A. B.5 C. D.6
5.如图,A、B两点在河的两岸,要测量这两点之间的距离,测量者在与A同侧的河岸边选定一点C,测出米,,,则等于( )米
A. B. C. D.
6.小颖在国际龙舟竞渡中心广场点处观看200米直道竞速赛.如图所示,赛道为东西方向,赛道起点位于点的北偏西方向上,终点位于点的北偏东方向上,米,则点到赛道的距离约为( )(参考数据:).
A.85.5米 B.86.6米 C.87.5米 D.88.5米
7.如图,将激光笔倾斜固定在长方体水槽A处,开启激光笔发射一束红光线,水槽中不装溶液介质时,发现光斑恰好落在处,此时,当向槽内缓缓加入溶液介质上升至处时,光斑随之缓缓移至处.已知为的中点,,,作出法线与的交点,测得折射角等于,则光斑移动的距离为( )
A. B. C. D.
8.如图,在平面直角坐标系中,点是坐标原点,点在函数的图象上.将直线沿轴向上平移,平移后的直线与轴交于点,与函数的图象交于点.若,则点的坐标是( )
A. B. C. D.
二、填空题
9.在中,若,,都是锐角,则的度数 .
10.如图,是的半径,是的弦,于点,是的切线,交的延长线于点.若,,则线段的长为 .
11.如图,一架无人机在滑雪赛道的一段坡道的上方进行跟踪拍摄,无人机伴随运动员水平向右飞行,某次拍摄中,当运动员在点位置时,无人机在他的仰角为的斜上方处,当运动员到达地面点时,无人机恰好到达运动员正上方的处,已知的坡度为且长为300米,无人机飞行距离为60米,则无人机离地面高度的长是 米.(参考数据:)
12.如图是水槽水龙头的侧面图,矩形为水槽侧面,宽,深,排水口位于的中点.在水槽边正上方安装水管,水龙头.按水龙头安装要求,水流需直接对准排水口确保水快速排入管道.测得,,则安装的水管的长为 .(精确到,参考数据:,,,)
13.如图,是的弦,半径于点D,连结.若的半径长为,的长为,则扇形的面积是 (结果保留).
14.勾股定理的证明方法丰富多样,其中我国古代数学家赵爽利用“弦图”的证明简明、直观,是世界公认最巧妙的方法.“赵爽弦图”已成为我国古代数学成就的一个重要标志,千百年来倍受人们的喜爱,小亮在如图所示的“赵爽弦图”中,连接,.若正方形与的边长之比为,则等于 .
三、解答题
15.计算:.
16.计算:.
17.如图,在中,E,F是对角线BD上的两点(点E在点F左侧),且.
(1)求证:四边形是平行四边形;
(2)当,,时,求的长.
18.如图,某小区有南北两个门,北门A在南门B的正北方,小红自小区北门A处出发,沿西南方向前往小区居民活动中心C处;小强自南门B处出发,沿正西方向行走300到达D处,再沿北偏西方向前往小区居民活动中心C处与小红汇合,两人所走的路程相同,求该小区北门A与南门B之间的距离.(结果保留根号)
19.如图,已知是的直径,为的内接三角形,为延长线上一点,连接于点,交于点.
(1)求证:是的切线.
(2)若,求的长.
20.如图所示,在中,,弦与弦交于点,弦与交于点,连接.
(1)求证:;
(2)若的直径长为,,求图中阴影部分面积.
21.如图,内接于,为的直径,延长至点D,使得.
(1)求证:是的切线;
(2)若,,求的长.
22.广州地铁经过多年的发展,地铁出入口更加人性化和便民化.如图1是某地铁出入口,有步梯和电梯两种由地下层通往地面层的出入方式.其截面如图2所示,是由地下直通地面的电梯,,,,,是步梯,,,的倾角相同,,与地面平行.已知电梯全长30米,倾角为,米.
(1)求地面层与地下层的垂直高度;
(2)求步梯的倾角的正切值和步梯通道的全长.参考数据:,,.
23.如图,⊙是的外接圆,是直径,,延长到点,使得,半径与交于点,连接与交于点.
(1)求证:是⊙的切线;
(2)若,求的长度;
(3)若是的中点,如图,求.
24.在平面直角坐标系中,抛物线经过点抛物线上点,的坐标分别为,.
(1)求抛物线的表达式;
(2)当时,求的取值范围;
(3)过点作轴的垂线,过点作轴的垂线,直线,交点为,以,为边作矩形.
①求;
②线段与轴相交于点,以为边作矩形,使矩形在轴同侧,且.当矩形与矩形重合部分图形的面积是矩形面积的时,求的值.
25.综合与实践:
主题:光的折射规律.
【实验操作】
第一步:将长方体空水槽放置在水平桌面上,束光线从林槽边沿A处投射到底部B处,入射光线与水槽内壁AC的夹角为;
第二步:向水槽注水,水面上升到的中点处时,停止注水.(直线为法线,为入射光线,为折射光线.)
【测量数据】
如图,点,,,,,,,,在同一平面内,测得,,折射角.
【问题解决】
根据以上实验操作和测量的数据,解答下列问题:
(1)求的长;
(2)求,之间的距离(结果精确到0.1cm):
(参考数据:,,)
26.如图,在平面直角坐标系中,正方形的边在轴的正半轴上,顶点,在第一象限内,正比例函数的图象经过点,反比例函数的图象经过点,且与边交于点,连接,已知.
(1)求的值;
(2)观察图象,请直接写出满足的的取值范围;
(3)连接,在线段上取一点,使,过点P作垂直轴,交双曲线于点,请求出线段的长.
试卷第1页,共3页
试卷第1页,共3页
《2025年甘肃省武威第二十中学中考数学人教版《锐角三角函数》专项练习题》参考答案
题号 1 2 3 4 5 6 7 8
答案 B C D B C B C B
9./度
10./
11.345
12.
13.
14.
15.解:
16.解:
.
17.(1)证明:,
,,
,
四边形是平行四边形,
,,
,
在和中,
,
,
,
四边形是平行四边形;
(2)解:在中,,
设,则,
由勾股定理得:,
解得:或(舍去),
,,
由(1)得:四边形是平行四边形,
,,
,
,
,
,
,
设,则,
,
解得:或,(舍去),
即.
18.解:过点C作于M,过D作于N,
又∵,
∴四边形是矩形,
∴,;
设,则;
∵,
∴,,
∴;
∵,
∴,,
∵两人所走的路程相同,
∴,即,
解得:;
∵,
∴
即小区北门A与南门B之间的距离为.
19.(1)证明:如图,连接,
,
,
,
,
∴
是的半径,
是的切线;.
(2)解:在中,,
,
是等边三角形,
,
是直径,
,
在中,.
20.(1)证明: ,
,又,
,
,即;
(2)解:连接,,过作,垂足为点,如图所示:
,
,
又,
,
在中,,
,
,
,
则.
21.(1)证明:连接,则:,
∴,
∵,
∴,
∵为的直径,
∴,
∴,
∴,即:,
∴,
又∵是的半径,
∴是的切线;
(2)∵,
∴,
在中,,
∴,
∵,,
∴△DCA∽△DBC
∴,
∴,
∴,即:,
解得:或(舍去);
∴.
22.(1)解:根据题意,得(米),
答:地面层与地下层的垂直高度约为18米.
(2)解:延长交于点M,延长交于点N,
∵,,的倾角相同,,与地面平行.
∴,
∴,
∵,
∴四边形,四边形都是平行四边形,
∴,
∵电梯全长30米,倾角为,米.
∴(米),
(米),
(米),
∴(米),
∴,
∴,
∴,
∴(米),
∴步梯通道的全长为(米).
23.(1)证明:是的直径,
,
,
,
,
即,
是的直径,
是的切线;
(2)解:,
,,
又,
,
,
,
,
;
(3)解:为直径,,
,
,
,
、,
,
、,
又,
是的中位线,
设,则,
,
,
解得:,
则、,
,
,
,
则.
24.(1)解:∵抛物线经过点,
∴,
∴,
∴抛物线的表达式为;
(2)解:当时,,
解得,,
∴抛物线与轴的交点坐标为和,
∴当时,;
当或时,;
①∵,,,
∴当时,,此时,
∴,
∵,
∴点在第四象限,即,
∴,
∴;
②当时,,
当点在第三象限,,
∴,
∴此时点在第四象限,即,
∴,不符合题意,舍去;
当点在第四象限,,
∴,
∵,
∴点在第一象限,即,
解得,
∴;
综上,或;
(3)解:①∵点,在抛物线上,
∴,,
如图,当点在第一象限,点在第四象限时,
,,
∴;
如图,当点在第四象限,点在第一象限时,
,,
∴;
②中,,
设,,
∴,
∴,
如图,当点在第一象限,点在第四象限时,
,
∵轴,
∴,
∴,
∴,
∵四边形为矩形,
∴,
∴,
∴,
∵,
∴,
∴,
∵,,
∴,
∴,
∴,
∴,
解得,(舍去);
如图,当点在第四象限,点在第一象限时,
同理可知,
此时,
∴,
解得(舍去),.
综上,m的值为或.
25.(1)解:在中,,
,
;
(2)解:由题可知,,
,
,
,
又,
,
.
26.(1)解:∵四边形是正方形,
∴,
在函数中,当时,,
∴点D的坐标为,
∵点D的坐标为且在反比例函数图象上,
∴,
∴,
∵正方形的边长为3,
∴,
把代入函数中,得,
∴,
∴,
∴;
(2)解:∵在函数中,当时,,
∴由图象可知的x的取值范围为;
(3)解:设直线的解析式为,代入点和得:
,
解得,
∴直线的解析式为,
过点作,交于点,
则,
∴,
∴,
∴,
∵,
∴设直线的解析式为:,把代入得:,
∴直线的解析式为,
∴当时,,
∴,
在反比例函数中,当时,,
∴,
∴.
答案第1页,共2页
答案第1页,共2页
同课章节目录
