2025年中考数学二轮复习-专题16二次函数与特殊几何图形【课件】(共53张PPT)
文档属性
| 名称 | 2025年中考数学二轮复习-专题16二次函数与特殊几何图形【课件】(共53张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-22 18:12:21 | ||
图片预览






文档简介
(共53张PPT)
专题十六 二次函数与特殊几何图形
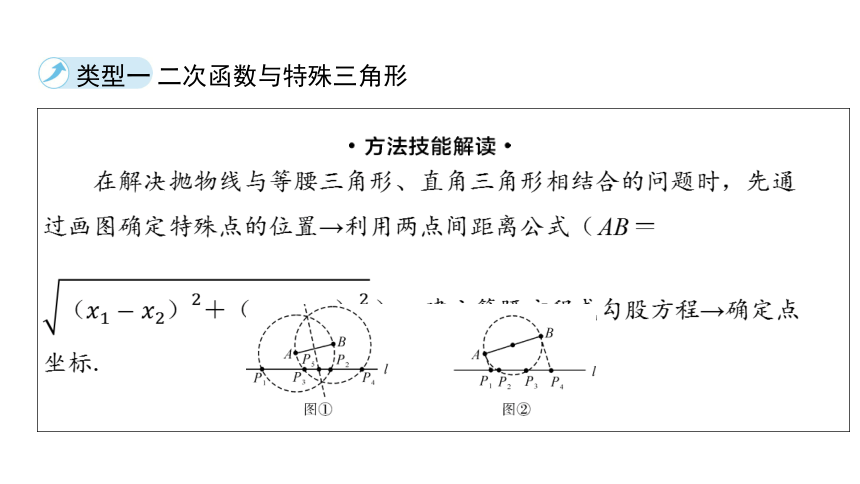
类型一 二次函数与特殊三角形
在解决抛物线与等腰三角形、直角三角形相结合的问题时,先通
过画图确定特殊点的位置→利用两点间距离公式(AB=
)→建立等腰方程或勾股方程→确定点
坐标.
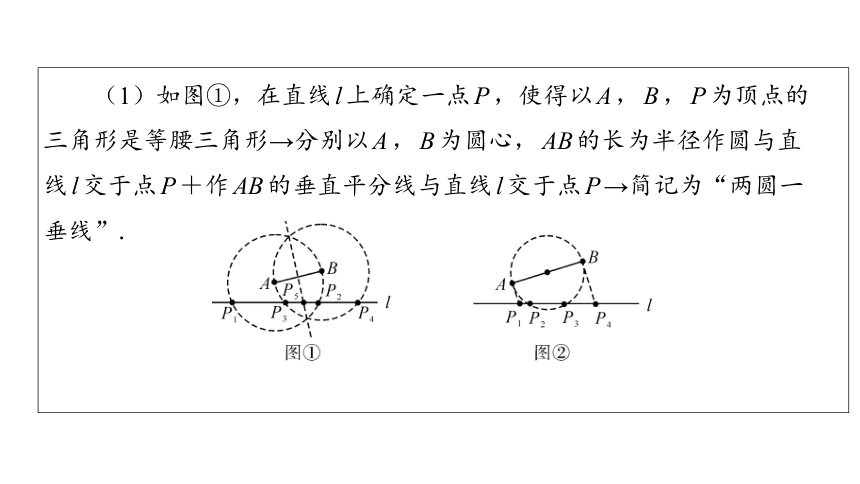
(1)如图①,在直线l上确定一点P,使得以A,B,P为顶点的
三角形是等腰三角形→分别以A,B为圆心,AB的长为半径作圆与直
线l交于点P+作AB的垂直平分线与直线l交于点P→简记为“两圆一
垂线”.
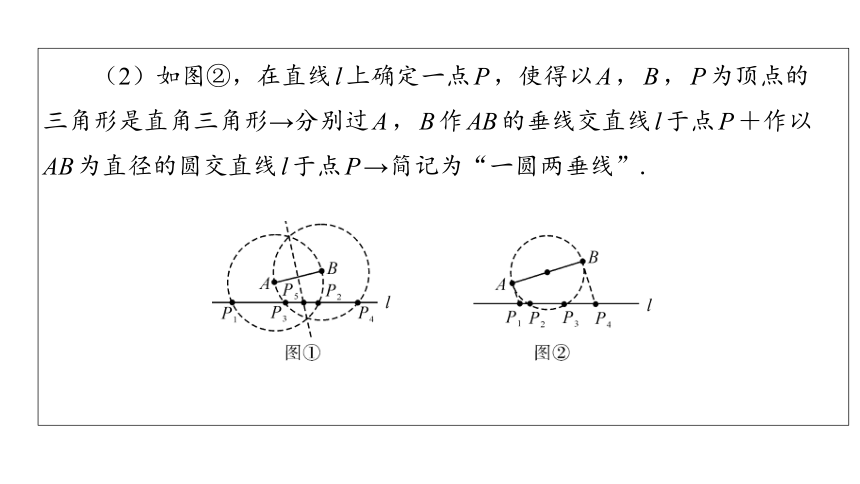
(2)如图②,在直线l上确定一点P,使得以A,B,P为顶点的
三角形是直角三角形→分别过A,B作AB的垂线交直线l于点P+作以
AB为直径的圆交直线l于点P→简记为“一圆两垂线”.
1. [2024·遂宁改编]如图,二次函数y=ax2+bx+c(a≠0)的图象与
x轴分别交于点A(-1,0),B(3,0),与y轴交于点C(0,-3),P,C两点关于抛物线的对称轴对称,Q为抛物线上一点.
(1)求二次函数的解析式;
解:(1)二次函数的解析式为y=x2-2x-3.
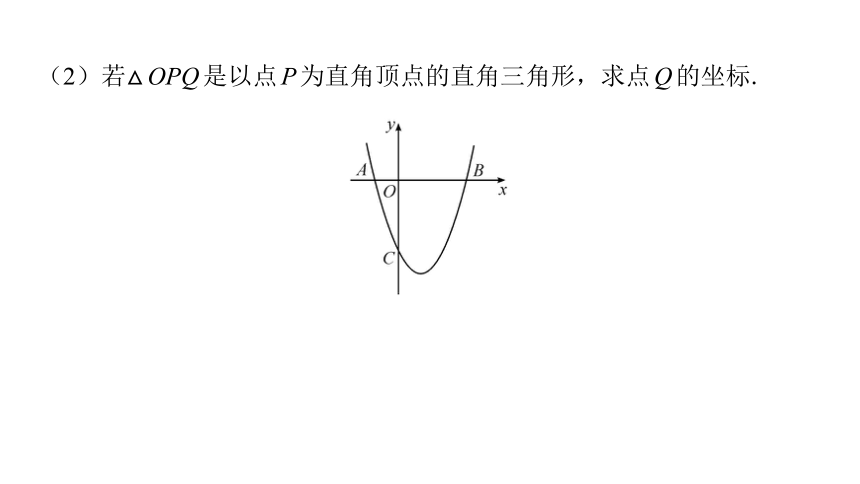
(2)若△OPQ是以点P为直角顶点的直角三角形,求点Q的坐标.
解:(2)如图,由(1)易得对称轴为直线x=1,
∴P(2,-3).设Q(m,m2-2m-3).
∵∠OPQ=90°,∴OP2+PQ2=OQ2,
∴[(0-2)2+(0+3)2]+[(2-m)2+ ]=
(0-m)2+ ,
整理可得3m2-8m+4=0,解得m1= ,m2=2(舍去),
∴点Q的坐标为( ,- ).
2. 如图,抛物线y=ax2+bx+4交x轴于A(-3,0),B(4,0)两
点,与y轴交于点C,连接AC,BC. M为线段OB上的一个动点,过点
M作PM⊥x轴,交抛物线于点P,交BC于点Q.
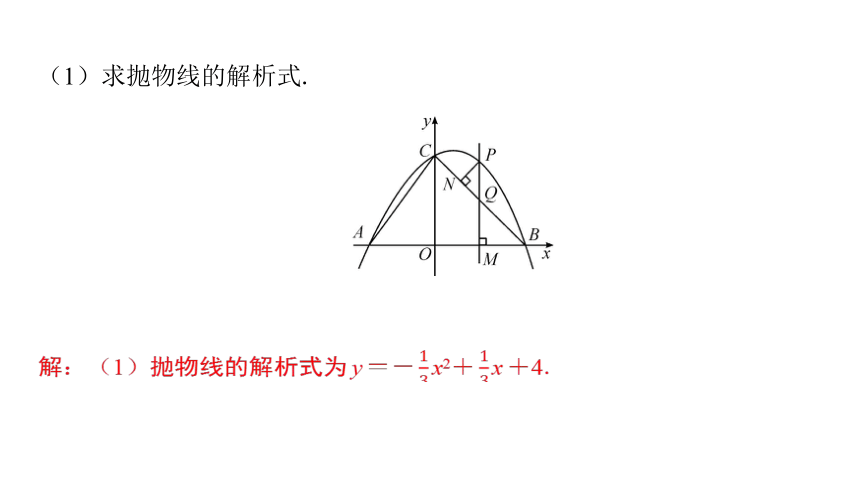
(1)求抛物线的解析式.
解:(1)抛物线的解析式为y=- x2+ x+4.
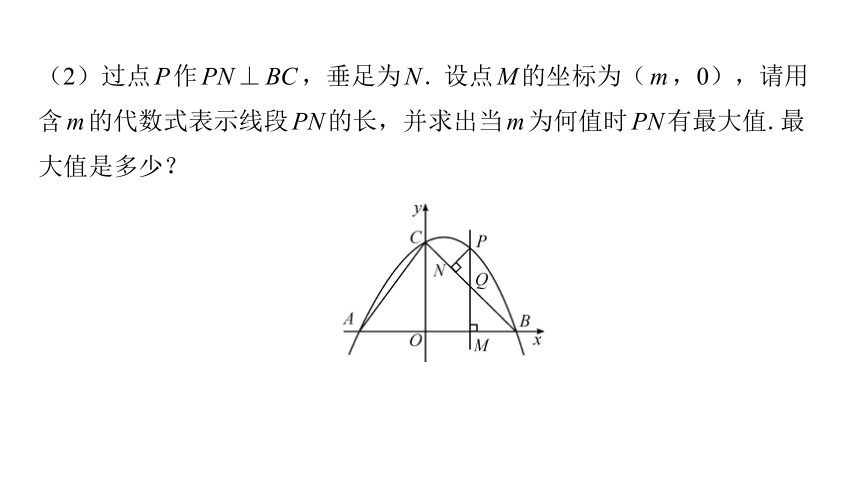
(2)过点P作PN⊥BC,垂足为N. 设点M的坐标为(m,0),请用
含m的代数式表示线段PN的长,并求出当m为何值时PN有最大值.最
大值是多少?
解:(2)易得点C的坐标为(0,4),由点B,C的坐标可得直线BC
的解析式为y=-x+4.
∵M(m,0),则P(m,- m2+ m+4),Q(m,-m+4),
∴PQ=- m2+ m+4+m-4=- m2+ m.
∵OB=OC,∴∠ABC=∠OCB=45°,PM∥y轴,∴∠PQN=
∠BQM=45°,
∴PN=PQ· sin 45°= (- m2+ m)=- (m-2)2+ ,
∴当m=2时,PN有最大值,最大值为 .
(3)点M在运动过程中,是否存在这样的点Q,使得以A,C,Q为
顶点的三角形是等腰三角形?若存在,请求出此时点Q的坐标;若不存
在,请说明理由.
(3)∵点A(-3,0),C(0,4),∴AC=5.设
点Q(m,-m+4).
①当AC=CQ时,如图,过点Q作QE⊥y轴于点E,则CQ2=EQ2+
CE2,即m2+[4-(-m+4)]2=52,
解得m= 或- (舍去),∴Q( , ).
②当AC=AQ时,AQ=AC=5.在Rt△AMQ中,[m-(-3)]2+(-
m+4)2=52,解得m=1或0(舍去),∴Q(1,3).
③当CQ=AQ时,2m2=[m-(-3)]2+(-m+4)2,解得m=
(舍去).
综上所述,点Q的坐标为( , )或(1,3).
3. 如图,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴
交于点C,其中B(1,0),C(0,3).
(1)求二次函数的解析式;
解:(1)二次函数的解析式为y=x2-4x+3.
(2)Q是对称轴l上一点,且点Q纵坐标为m,当△QAC是锐角三角形
时,求m的取值范围.
解:(2)如图,过点C作CE⊥AC交对称轴于点E,过点A作AF⊥AC交对称轴于点F,
作以AC为直径的圆交对称轴于M,N两点,则△AEC,
△AMC,△ANC,△AFC是直角三角形.
∵△QAC是锐角三角形,∴点Q应在线段EM,NF上(端点除外).
设直线x=2上的动点坐标为(2,m).∵A(3,0),C(0,3),∴AC2=18.
①当∠ACE=90°时,AC2+CE2=AE2,
∴18+(m-3)2+(2-0)2=m2+(2-3)2,解得m=5,∴E
(2,5).
②当∠CAF=90°时,AC2+AF2=CF2,
∴18+m2+(2-3)2=(m-3)2+(2-0)2,解得m=-1,∴F
(2,-1).
③当动点(2,m)在圆上时,(m-3)2+(2-0)2+m2+(2-3)2
=18,即m2-3m-2=0,
解得m= ,∴M(2, ),N(2, ).
综上所述,当△QAC是锐角三角形时,m的取值范围为 <m<5或
-1<m< .
类型二 二次函数与特殊四边形
在解决抛物线与平行四边形、矩形、菱形、正方形相结合的问题
时,关键要结合点的平移规律描述点的坐标+线段中点坐标公式+特
殊平行四边形的几何特征→建立特殊点的坐标参量方程组→确定特殊
点坐标,同时,要注意分类讨论.
(1)如图①,“三定点(A,B,C)+一动点(D)”→利用
点的平移规律描述动点D坐标.
(2)如图②,“两定点(A,B)+两动点(M,N)”→利用
对角线的交点平分对角线→建立动点坐标参量方程组
(3)若遇到矩形、菱形、正方形时,在(2)的坐标参量方程组
中,再附加一个矩形(对角线相等)、菱形(一组邻边相等)、正方
形(一组邻边相等+对角线相等)的特性建立坐标参量方程.
1. 如图,抛物线y=-x2+bx+c经过A(-1,0),C(0,3)两
点,并交x轴于另一点B,M是抛物线的顶点,直线AM与y轴交于点
D.
(1)求抛物线的解析式.
解:(1)抛物线的解析式为y=-x2+2x+3.
(2)若P是抛物线上一动点,则在对称轴上是否存在点Q,使得以
D,M,P,Q为顶点的四边形是平行四边形?若存在,请直接写出所
有满足条件的点Q的坐标;若不存在,请说明理由.
解:(2)易得对称轴为直线x=1,M(1,4),D(0,2).设Q
(1,n),P(m,-m2+2m+3).
如图①,当DM为对角线时, 解得
∴Q(1,3).
如图②,当MQ为对角线时, 解得
∴Q(1,1).
如图③,当MP为对角线时, 解得
∴Q(1,5).
综上所述,存在满足题意的点Q,点Q的坐标为
(1,3)或(1,1)或(1,5).
2. 如图,抛物线y=ax2+2x+c的对称轴是直线x=1,与x轴交于点
A,B(3,0),与y轴交于点C,连接AC.
(1)求抛物线的解析式.
解:(1)抛物线的解析式为y=-x2+2x+3.
(2)已知E是抛物线对称轴上的点,在坐标平面内是否存在点F,使
以点B,C,E,F为顶点四边形为矩形?若存在,求出点F的坐标;
若不存在,请说明理由.
解:(2)由(1)易得A(-1,0),B(3,0),C(0,3).设E
(1,n),F(s,t).分以下两种情况讨论:
如图①,当BC为矩形的边时,由矩形的对角线交点为对角线的中点及
矩形的对角线相等,
得
解得
∴点F的坐标为(4,1)或(-2,1).
如图②,当BC为矩形的对角线时,以BC为直径作圆可确定点E的位
置,由矩形的对角线交点为对角线的中点及矩形的对角线相等,
得 解得
∴点F的坐标为(2, )或(2, ).
综上所述,点F的坐标为(4,1)或(-2,1)或(2, )或(2,
).
3. 如图,抛物线y=ax2-2x+c与x轴交于A,B两点,与y轴交于点
C,△AOC是等腰直角三角形,且面积为 .
(1)求抛物线和直线AC的解析式;
解:(1)抛物线的解析式为y=-x2-2x+3,直线AC的解析式为
y=x+3.
(2)若P是直线AC上的动点,Q是平面内一点,当以B,C,P,Q
为顶点的四边形是菱形时,求点Q的坐标.
解:(2)易得B(1,0),C(0,3).设P(r,r+3),
Q(m,n),
则BC2=10,BP2=(1-r)2+ =2r2+4r+10,
CP2=(0-r)2+ =2r2.
如图①,当BC为边,且BC=BP时,
解得 ∵当r=0时,P
(0,3)与点C重合,舍去,∴Q(-3,4).
如图②,当BC为边,且CB=CP时,
解得 ∴Q(
+1, )或Q(- +1,- ).
如图③,当BC为对角线,且PC=PB时,
解得 ∴Q( , ).
综上所述,当以B,C,P,Q为顶点的四边形是菱形时,点Q的坐标
为(-3,4)或( +1, )或(- +1,- )或( , ).
类型三 二次函数与圆
在解决抛物线与圆相结合的问题时,关键要利用抛物线上的动点
坐标描述与圆相关的线段→结合圆的相关性质建立动点坐标参量方程
→确定特殊点坐标.
1. 如图,抛物线y=x2-2x-3的对称轴与x轴交于点M,☉M与y轴相
切,P是抛物线上一动点,作PQ与☉M相切于点Q,求PQ的最小值.
解:如图,连接PM,MQ.
由y=x2-2x-3易得抛物线的对称轴为直线x=1,∴M(1,0).
∵☉M与y轴相切,∴☉M的半径为1.
设P(x,x2-2x-3),则PM2=(x-1)2+ =
(x-1)2+ ,
令n=(x-1)2,则PM2=n+(n-4)2= + ,
∴当n= 时,PM2的最小值为 .
∵PQ与☉M相切于点Q,∴PQ2=PM2-MQ2=PM2-1,
∴PQ2的最小值为 -1= ,∴PQ的最小值为 = .
2. 如图,抛物线y=ax2+ x+c经过点A(-1,0)和点C(0,3),
与x轴的另一交点为点B. M是直线BC上一动点,过点M作MP∥y
轴,交抛物线于点P.
(1)求抛物线的解析式.
解:(1)抛物线的解析式为y=- x2+ x+3.
(2)在抛物线上是否存在一点Q,使得△QCO是等边三角形?若存
在,求出点Q的坐标;若不存在,请说明理由.
解:(2)不存在.理由如下:
∵OC=3,∴以OC为边的等边三角形QCO的顶点Q在OC的垂直平分
线y= 上,
∴点Q的横坐标为 或 ,
∴点Q的坐标为(± , ),当x=± 时,y=- x2+ x+
3≠ ,
∴等边三角形QCO的顶点Q不在抛物线上,∴抛物线上不存在点Q,
使得△QCO是等边三角形.
(3)以M为圆心,MP为半径作☉M,当☉M与坐标轴相切时,求出
☉M的半径.
解:(3)令y=0,即- x2+ x+3=0,解得x=-1或x=4,∴B
(4,0),易得直线BC的解析式为y=- x+3.
设M(m,- m+3),0<m<4,则P(m,- m2+ m+3),
∴PM= .
①当☉M与y轴相切时,有 = ,即 m2-3m=m或 m2
-3m=-m,
解得m=0(舍去)或m= 或m= ,∴☉M的半径为 或 .
②当☉M与x轴相切时,有 = ,即 m2-3m=
- m+3或 m2-3m= m-3,
解得m=4(舍去)或m=-1或m=1,∴☉M的半径为 或 .
综上所述,当☉M与坐标轴相切时,☉M的半径为 或 或 或 .
谢谢观看
专题十六 二次函数与特殊几何图形
类型一 二次函数与特殊三角形
在解决抛物线与等腰三角形、直角三角形相结合的问题时,先通
过画图确定特殊点的位置→利用两点间距离公式(AB=
)→建立等腰方程或勾股方程→确定点
坐标.
(1)如图①,在直线l上确定一点P,使得以A,B,P为顶点的
三角形是等腰三角形→分别以A,B为圆心,AB的长为半径作圆与直
线l交于点P+作AB的垂直平分线与直线l交于点P→简记为“两圆一
垂线”.
(2)如图②,在直线l上确定一点P,使得以A,B,P为顶点的
三角形是直角三角形→分别过A,B作AB的垂线交直线l于点P+作以
AB为直径的圆交直线l于点P→简记为“一圆两垂线”.
1. [2024·遂宁改编]如图,二次函数y=ax2+bx+c(a≠0)的图象与
x轴分别交于点A(-1,0),B(3,0),与y轴交于点C(0,-3),P,C两点关于抛物线的对称轴对称,Q为抛物线上一点.
(1)求二次函数的解析式;
解:(1)二次函数的解析式为y=x2-2x-3.
(2)若△OPQ是以点P为直角顶点的直角三角形,求点Q的坐标.
解:(2)如图,由(1)易得对称轴为直线x=1,
∴P(2,-3).设Q(m,m2-2m-3).
∵∠OPQ=90°,∴OP2+PQ2=OQ2,
∴[(0-2)2+(0+3)2]+[(2-m)2+ ]=
(0-m)2+ ,
整理可得3m2-8m+4=0,解得m1= ,m2=2(舍去),
∴点Q的坐标为( ,- ).
2. 如图,抛物线y=ax2+bx+4交x轴于A(-3,0),B(4,0)两
点,与y轴交于点C,连接AC,BC. M为线段OB上的一个动点,过点
M作PM⊥x轴,交抛物线于点P,交BC于点Q.
(1)求抛物线的解析式.
解:(1)抛物线的解析式为y=- x2+ x+4.
(2)过点P作PN⊥BC,垂足为N. 设点M的坐标为(m,0),请用
含m的代数式表示线段PN的长,并求出当m为何值时PN有最大值.最
大值是多少?
解:(2)易得点C的坐标为(0,4),由点B,C的坐标可得直线BC
的解析式为y=-x+4.
∵M(m,0),则P(m,- m2+ m+4),Q(m,-m+4),
∴PQ=- m2+ m+4+m-4=- m2+ m.
∵OB=OC,∴∠ABC=∠OCB=45°,PM∥y轴,∴∠PQN=
∠BQM=45°,
∴PN=PQ· sin 45°= (- m2+ m)=- (m-2)2+ ,
∴当m=2时,PN有最大值,最大值为 .
(3)点M在运动过程中,是否存在这样的点Q,使得以A,C,Q为
顶点的三角形是等腰三角形?若存在,请求出此时点Q的坐标;若不存
在,请说明理由.
(3)∵点A(-3,0),C(0,4),∴AC=5.设
点Q(m,-m+4).
①当AC=CQ时,如图,过点Q作QE⊥y轴于点E,则CQ2=EQ2+
CE2,即m2+[4-(-m+4)]2=52,
解得m= 或- (舍去),∴Q( , ).
②当AC=AQ时,AQ=AC=5.在Rt△AMQ中,[m-(-3)]2+(-
m+4)2=52,解得m=1或0(舍去),∴Q(1,3).
③当CQ=AQ时,2m2=[m-(-3)]2+(-m+4)2,解得m=
(舍去).
综上所述,点Q的坐标为( , )或(1,3).
3. 如图,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴
交于点C,其中B(1,0),C(0,3).
(1)求二次函数的解析式;
解:(1)二次函数的解析式为y=x2-4x+3.
(2)Q是对称轴l上一点,且点Q纵坐标为m,当△QAC是锐角三角形
时,求m的取值范围.
解:(2)如图,过点C作CE⊥AC交对称轴于点E,过点A作AF⊥AC交对称轴于点F,
作以AC为直径的圆交对称轴于M,N两点,则△AEC,
△AMC,△ANC,△AFC是直角三角形.
∵△QAC是锐角三角形,∴点Q应在线段EM,NF上(端点除外).
设直线x=2上的动点坐标为(2,m).∵A(3,0),C(0,3),∴AC2=18.
①当∠ACE=90°时,AC2+CE2=AE2,
∴18+(m-3)2+(2-0)2=m2+(2-3)2,解得m=5,∴E
(2,5).
②当∠CAF=90°时,AC2+AF2=CF2,
∴18+m2+(2-3)2=(m-3)2+(2-0)2,解得m=-1,∴F
(2,-1).
③当动点(2,m)在圆上时,(m-3)2+(2-0)2+m2+(2-3)2
=18,即m2-3m-2=0,
解得m= ,∴M(2, ),N(2, ).
综上所述,当△QAC是锐角三角形时,m的取值范围为 <m<5或
-1<m< .
类型二 二次函数与特殊四边形
在解决抛物线与平行四边形、矩形、菱形、正方形相结合的问题
时,关键要结合点的平移规律描述点的坐标+线段中点坐标公式+特
殊平行四边形的几何特征→建立特殊点的坐标参量方程组→确定特殊
点坐标,同时,要注意分类讨论.
(1)如图①,“三定点(A,B,C)+一动点(D)”→利用
点的平移规律描述动点D坐标.
(2)如图②,“两定点(A,B)+两动点(M,N)”→利用
对角线的交点平分对角线→建立动点坐标参量方程组
(3)若遇到矩形、菱形、正方形时,在(2)的坐标参量方程组
中,再附加一个矩形(对角线相等)、菱形(一组邻边相等)、正方
形(一组邻边相等+对角线相等)的特性建立坐标参量方程.
1. 如图,抛物线y=-x2+bx+c经过A(-1,0),C(0,3)两
点,并交x轴于另一点B,M是抛物线的顶点,直线AM与y轴交于点
D.
(1)求抛物线的解析式.
解:(1)抛物线的解析式为y=-x2+2x+3.
(2)若P是抛物线上一动点,则在对称轴上是否存在点Q,使得以
D,M,P,Q为顶点的四边形是平行四边形?若存在,请直接写出所
有满足条件的点Q的坐标;若不存在,请说明理由.
解:(2)易得对称轴为直线x=1,M(1,4),D(0,2).设Q
(1,n),P(m,-m2+2m+3).
如图①,当DM为对角线时, 解得
∴Q(1,3).
如图②,当MQ为对角线时, 解得
∴Q(1,1).
如图③,当MP为对角线时, 解得
∴Q(1,5).
综上所述,存在满足题意的点Q,点Q的坐标为
(1,3)或(1,1)或(1,5).
2. 如图,抛物线y=ax2+2x+c的对称轴是直线x=1,与x轴交于点
A,B(3,0),与y轴交于点C,连接AC.
(1)求抛物线的解析式.
解:(1)抛物线的解析式为y=-x2+2x+3.
(2)已知E是抛物线对称轴上的点,在坐标平面内是否存在点F,使
以点B,C,E,F为顶点四边形为矩形?若存在,求出点F的坐标;
若不存在,请说明理由.
解:(2)由(1)易得A(-1,0),B(3,0),C(0,3).设E
(1,n),F(s,t).分以下两种情况讨论:
如图①,当BC为矩形的边时,由矩形的对角线交点为对角线的中点及
矩形的对角线相等,
得
解得
∴点F的坐标为(4,1)或(-2,1).
如图②,当BC为矩形的对角线时,以BC为直径作圆可确定点E的位
置,由矩形的对角线交点为对角线的中点及矩形的对角线相等,
得 解得
∴点F的坐标为(2, )或(2, ).
综上所述,点F的坐标为(4,1)或(-2,1)或(2, )或(2,
).
3. 如图,抛物线y=ax2-2x+c与x轴交于A,B两点,与y轴交于点
C,△AOC是等腰直角三角形,且面积为 .
(1)求抛物线和直线AC的解析式;
解:(1)抛物线的解析式为y=-x2-2x+3,直线AC的解析式为
y=x+3.
(2)若P是直线AC上的动点,Q是平面内一点,当以B,C,P,Q
为顶点的四边形是菱形时,求点Q的坐标.
解:(2)易得B(1,0),C(0,3).设P(r,r+3),
Q(m,n),
则BC2=10,BP2=(1-r)2+ =2r2+4r+10,
CP2=(0-r)2+ =2r2.
如图①,当BC为边,且BC=BP时,
解得 ∵当r=0时,P
(0,3)与点C重合,舍去,∴Q(-3,4).
如图②,当BC为边,且CB=CP时,
解得 ∴Q(
+1, )或Q(- +1,- ).
如图③,当BC为对角线,且PC=PB时,
解得 ∴Q( , ).
综上所述,当以B,C,P,Q为顶点的四边形是菱形时,点Q的坐标
为(-3,4)或( +1, )或(- +1,- )或( , ).
类型三 二次函数与圆
在解决抛物线与圆相结合的问题时,关键要利用抛物线上的动点
坐标描述与圆相关的线段→结合圆的相关性质建立动点坐标参量方程
→确定特殊点坐标.
1. 如图,抛物线y=x2-2x-3的对称轴与x轴交于点M,☉M与y轴相
切,P是抛物线上一动点,作PQ与☉M相切于点Q,求PQ的最小值.
解:如图,连接PM,MQ.
由y=x2-2x-3易得抛物线的对称轴为直线x=1,∴M(1,0).
∵☉M与y轴相切,∴☉M的半径为1.
设P(x,x2-2x-3),则PM2=(x-1)2+ =
(x-1)2+ ,
令n=(x-1)2,则PM2=n+(n-4)2= + ,
∴当n= 时,PM2的最小值为 .
∵PQ与☉M相切于点Q,∴PQ2=PM2-MQ2=PM2-1,
∴PQ2的最小值为 -1= ,∴PQ的最小值为 = .
2. 如图,抛物线y=ax2+ x+c经过点A(-1,0)和点C(0,3),
与x轴的另一交点为点B. M是直线BC上一动点,过点M作MP∥y
轴,交抛物线于点P.
(1)求抛物线的解析式.
解:(1)抛物线的解析式为y=- x2+ x+3.
(2)在抛物线上是否存在一点Q,使得△QCO是等边三角形?若存
在,求出点Q的坐标;若不存在,请说明理由.
解:(2)不存在.理由如下:
∵OC=3,∴以OC为边的等边三角形QCO的顶点Q在OC的垂直平分
线y= 上,
∴点Q的横坐标为 或 ,
∴点Q的坐标为(± , ),当x=± 时,y=- x2+ x+
3≠ ,
∴等边三角形QCO的顶点Q不在抛物线上,∴抛物线上不存在点Q,
使得△QCO是等边三角形.
(3)以M为圆心,MP为半径作☉M,当☉M与坐标轴相切时,求出
☉M的半径.
解:(3)令y=0,即- x2+ x+3=0,解得x=-1或x=4,∴B
(4,0),易得直线BC的解析式为y=- x+3.
设M(m,- m+3),0<m<4,则P(m,- m2+ m+3),
∴PM= .
①当☉M与y轴相切时,有 = ,即 m2-3m=m或 m2
-3m=-m,
解得m=0(舍去)或m= 或m= ,∴☉M的半径为 或 .
②当☉M与x轴相切时,有 = ,即 m2-3m=
- m+3或 m2-3m= m-3,
解得m=4(舍去)或m=-1或m=1,∴☉M的半径为 或 .
综上所述,当☉M与坐标轴相切时,☉M的半径为 或 或 或 .
谢谢观看
同课章节目录
