北京市第二中学2024-2025学年高一下学期段考四数学试题(含答案)
文档属性
| 名称 | 北京市第二中学2024-2025学年高一下学期段考四数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 605.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-22 21:43:15 | ||
图片预览



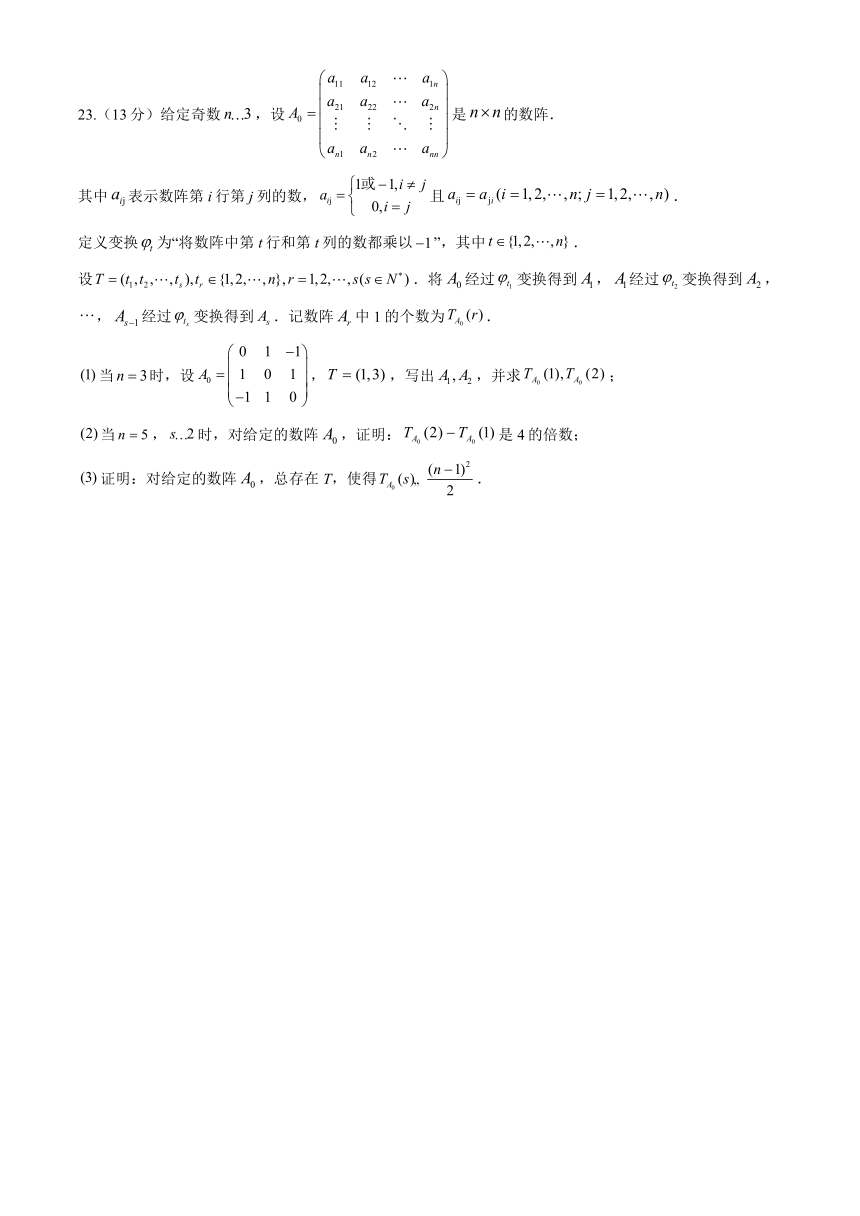
文档简介
2025北京二中高一(下)段考四
数 学
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的选项中,只有一项是符合题目要求的,请将答案填在答题纸上)
1.已知集合,,则等于
A. B. C. D.
2.已知向量,,则的坐标为
A. B. C. D.
3.已知向量,,若,则实数的值为
A. B. C. 2 D.
4.已知向量,,若,则的值为
A. B. C. D. 10
5.将函数y=sin的图象上各点的纵坐标不变,横坐标伸长到原来的2倍,再向右平移个单位长度,所得到的图象的解析式是
A.y=sin x B.y=cos x C.y=sin 4x D.y=cos 4x
6.在中,A,B,C所对的边为a,b,c,已知,,,则的值为
A. B. C. D.
7.若实数a,b满足,,则“”是“”成立的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
8.若非零向量与满足,,则为
A. 三边均不相等的三角形 B. 直角三角形
C. 等边三角形 D. 底边和腰不相等的等腰三角形
9.在ABC中,角A、B、C所对的边分别为,S表示ABC的面积,
若,,则角B等于
A.90 B.60 C.45 D.30
10.已知是边长为2的等边三角形,P为平面ABC内一点,则的最小值是
A. B. C. D.
11.若 均为单位向量,且,,则的最大值为
A. B. C. D.
12.在坐标平面内,横、纵坐标均为整数的点称为整点.点从原点出发,在坐标平面内跳跃行进,每次跳跃的长度都是且落在整点处.则点到达点所跳跃次数的最小值是
A.9 B.10 C.11 D.12
二、填空题(本大题共6小题,每小题5分,共30分. 请将答案填在答题纸上)
13.已知,且,则实数的值为 .
14.在中,,,且的面积为,则AC长为 .
15.已知函数,方程在[,]内解的个数为________.
16.已知均为锐角,,,则= ,= .
17.如图,在同一平面内,,,的长分别为,,,与的夹角为,且,与的夹角为.若,
则的值为____________.
18.主动降噪耳机让我们在嘈杂的环境中享受一丝宁静,它的工作原理是:先通过微型麦克风采集周围的噪声,然后降噪芯片生成与振幅相同的反相位声波来抵消噪声,已知某噪声的声波曲线为
,且经过点,给出以下四个命题:
①函数是奇函数;
②函数在区间上单调递减;
③,使得;
④存在常数m,对于,都有.
其中正确的命题为_________________(请写出所有正确命题的序号).
三、解答题(本题共5小题,共60分,请将答案填在答题纸上)
19. (10分)已知,,,求:
;
与的夹角的余弦值.
20. (12分)已知函数的周期为
求的值及函数的单调递增区间;
若,求的最大值和最小值以及取得最值时相应的值.
21. (12分)在中,a,b,c分别为角A,B,C所对的边且,
求角B的值;
若为锐角三角形,且,求的面积的取值范围.
22. (13分)已知函数,关于x的不等式的解集为.
求实数a,b的值;
求关于x的不等式的解集;
若不等式在R上恒成立,求实数k的取值范围.
23.(13分)给定奇数,设是的数阵.
其中表示数阵第i行第j列的数,且.
定义变换为“将数阵中第t行和第t列的数都乘以”,其中.
设.将经过变换得到,经过变换得到,,经过变换得到.记数阵中1的个数为.
当时,设,,写出,并求;
当,时,对给定的数阵,证明:是4的倍数;
证明:对给定的数阵,总存在T,使得.
参考答案
选择题
1 2 3 4 5 6 7 8 9 10 11 12
A B A B A A C C C B B B
二、填空题
13.
14.
15. 4
16. ,
17.
18.①②④
三、解答题
19.【答案】解:,
又,,
解得
由可得,
与的夹角的余弦值为
20.【答案】解:
由于函数的最小正周期为,
所以,
故,
令,
解得,
故函数的单调递增区间为
由于,
所以,
所以,
所以当,即时, ;
所以当,即时, .
21.【答案】解:由正弦定理得:,
即,
又,可得,
,
由正弦定理得:, ,
,
锐角三角形ABC,,
,
22.【答案】解:,则,
又的解集为,方程的两根为1和
,;
由可得,
因为,所以,,
所以,可得,
又在中,,
故当时,原不等式的解集为;当时,原不等式的解集为;
当时,原不等式的解集为;当时,原不等式的解集为;
由可得,
因为 ,即,
可得,
令,即在区间上恒成立,
方法一:设函数,,
①若在上单调递减,在上单调递增,
,解得,故此时
②若在上单调递增,此时,即 ,
综上:k的取值范围是
方法二:由在上恒成立,即在上恒成立,
令,则,
即在上恒成立,即在上恒成立,
当且仅当时取等号,
,当且仅当时取等号,
23.【答案】解:由题设,
所以,
设数阵中第行和第列中1的个数均为,的个数均为
经过变换,的第行和第列均有个1变为,有个变为
所以
即是4的倍数.
数阵经过变换得到数阵,设的第行和第列中1的个数均为
由可知,
设当时,取得最小值,其中
记每行中1的个数为,,,则必有,
否则,若存在j使得,则令,有
,与为最小值矛盾.
在,,,中,
①若等于的个数不超过,
则
②若等于的个数大于,则必存在i,j满足,且
否则,不妨设,则共有个j满足,且,
所以,,,中至多有个等于,矛盾.
故存在i,j满足,且
取,因为,所以
由变换为时,数阵第i行中1的个数为
故,
这与为最小值矛盾.
综上,对给定的数阵,总存在T,使得
数 学
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的选项中,只有一项是符合题目要求的,请将答案填在答题纸上)
1.已知集合,,则等于
A. B. C. D.
2.已知向量,,则的坐标为
A. B. C. D.
3.已知向量,,若,则实数的值为
A. B. C. 2 D.
4.已知向量,,若,则的值为
A. B. C. D. 10
5.将函数y=sin的图象上各点的纵坐标不变,横坐标伸长到原来的2倍,再向右平移个单位长度,所得到的图象的解析式是
A.y=sin x B.y=cos x C.y=sin 4x D.y=cos 4x
6.在中,A,B,C所对的边为a,b,c,已知,,,则的值为
A. B. C. D.
7.若实数a,b满足,,则“”是“”成立的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
8.若非零向量与满足,,则为
A. 三边均不相等的三角形 B. 直角三角形
C. 等边三角形 D. 底边和腰不相等的等腰三角形
9.在ABC中,角A、B、C所对的边分别为,S表示ABC的面积,
若,,则角B等于
A.90 B.60 C.45 D.30
10.已知是边长为2的等边三角形,P为平面ABC内一点,则的最小值是
A. B. C. D.
11.若 均为单位向量,且,,则的最大值为
A. B. C. D.
12.在坐标平面内,横、纵坐标均为整数的点称为整点.点从原点出发,在坐标平面内跳跃行进,每次跳跃的长度都是且落在整点处.则点到达点所跳跃次数的最小值是
A.9 B.10 C.11 D.12
二、填空题(本大题共6小题,每小题5分,共30分. 请将答案填在答题纸上)
13.已知,且,则实数的值为 .
14.在中,,,且的面积为,则AC长为 .
15.已知函数,方程在[,]内解的个数为________.
16.已知均为锐角,,,则= ,= .
17.如图,在同一平面内,,,的长分别为,,,与的夹角为,且,与的夹角为.若,
则的值为____________.
18.主动降噪耳机让我们在嘈杂的环境中享受一丝宁静,它的工作原理是:先通过微型麦克风采集周围的噪声,然后降噪芯片生成与振幅相同的反相位声波来抵消噪声,已知某噪声的声波曲线为
,且经过点,给出以下四个命题:
①函数是奇函数;
②函数在区间上单调递减;
③,使得;
④存在常数m,对于,都有.
其中正确的命题为_________________(请写出所有正确命题的序号).
三、解答题(本题共5小题,共60分,请将答案填在答题纸上)
19. (10分)已知,,,求:
;
与的夹角的余弦值.
20. (12分)已知函数的周期为
求的值及函数的单调递增区间;
若,求的最大值和最小值以及取得最值时相应的值.
21. (12分)在中,a,b,c分别为角A,B,C所对的边且,
求角B的值;
若为锐角三角形,且,求的面积的取值范围.
22. (13分)已知函数,关于x的不等式的解集为.
求实数a,b的值;
求关于x的不等式的解集;
若不等式在R上恒成立,求实数k的取值范围.
23.(13分)给定奇数,设是的数阵.
其中表示数阵第i行第j列的数,且.
定义变换为“将数阵中第t行和第t列的数都乘以”,其中.
设.将经过变换得到,经过变换得到,,经过变换得到.记数阵中1的个数为.
当时,设,,写出,并求;
当,时,对给定的数阵,证明:是4的倍数;
证明:对给定的数阵,总存在T,使得.
参考答案
选择题
1 2 3 4 5 6 7 8 9 10 11 12
A B A B A A C C C B B B
二、填空题
13.
14.
15. 4
16. ,
17.
18.①②④
三、解答题
19.【答案】解:,
又,,
解得
由可得,
与的夹角的余弦值为
20.【答案】解:
由于函数的最小正周期为,
所以,
故,
令,
解得,
故函数的单调递增区间为
由于,
所以,
所以,
所以当,即时, ;
所以当,即时, .
21.【答案】解:由正弦定理得:,
即,
又,可得,
,
由正弦定理得:, ,
,
锐角三角形ABC,,
,
22.【答案】解:,则,
又的解集为,方程的两根为1和
,;
由可得,
因为,所以,,
所以,可得,
又在中,,
故当时,原不等式的解集为;当时,原不等式的解集为;
当时,原不等式的解集为;当时,原不等式的解集为;
由可得,
因为 ,即,
可得,
令,即在区间上恒成立,
方法一:设函数,,
①若在上单调递减,在上单调递增,
,解得,故此时
②若在上单调递增,此时,即 ,
综上:k的取值范围是
方法二:由在上恒成立,即在上恒成立,
令,则,
即在上恒成立,即在上恒成立,
当且仅当时取等号,
,当且仅当时取等号,
23.【答案】解:由题设,
所以,
设数阵中第行和第列中1的个数均为,的个数均为
经过变换,的第行和第列均有个1变为,有个变为
所以
即是4的倍数.
数阵经过变换得到数阵,设的第行和第列中1的个数均为
由可知,
设当时,取得最小值,其中
记每行中1的个数为,,,则必有,
否则,若存在j使得,则令,有
,与为最小值矛盾.
在,,,中,
①若等于的个数不超过,
则
②若等于的个数大于,则必存在i,j满足,且
否则,不妨设,则共有个j满足,且,
所以,,,中至多有个等于,矛盾.
故存在i,j满足,且
取,因为,所以
由变换为时,数阵第i行中1的个数为
故,
这与为最小值矛盾.
综上,对给定的数阵,总存在T,使得
同课章节目录
