8.3用正多边形铺设地面 课件(共23张PPT)
文档属性
| 名称 | 8.3用正多边形铺设地面 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 06:55:38 | ||
图片预览






文档简介
(共23张PPT)
(华师大版)七年级
下
8.3用正多边形铺设地面
三角形
第8章
“八”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.通过用相同的正多边形铺地面的活动,巩固多边形的内角和与外角和公式;
2.通过“铺地面”和相关计算,使学生从中发现能拼成一个不留空隙,又不重叠的平面图形的关键是几个多边形的内角和相加要等于360°.
新知导入
问题1:多边形的内角和、外角和.
n 边形的内角和为(n2)×180°,外角和为360°.
问题2:正多边形的一个内角和一个外角怎样计算?
正 n 边形的一个内角为,一个外角为.
新知导入
思考:这些地砖都是什么形状?为什么能铺满地面而不留一点空隙呢?换一些其他形状的行不行?
新知讲解
围绕某一顶点铺满地面
生活中常常用瓷砖严丝合缝、不留空隙地铺满墙面或地面. 从数学的角度看,就是用几何图形不留空隙、不重叠地铺满平面的一部分,这就是平面图形的镶嵌.
新知讲解
使用给定的某种正多边形,它能否铺满地面,既不留下一丝空白,又不互相重叠呢?
与正多边形的内角大小有关
新知讲解
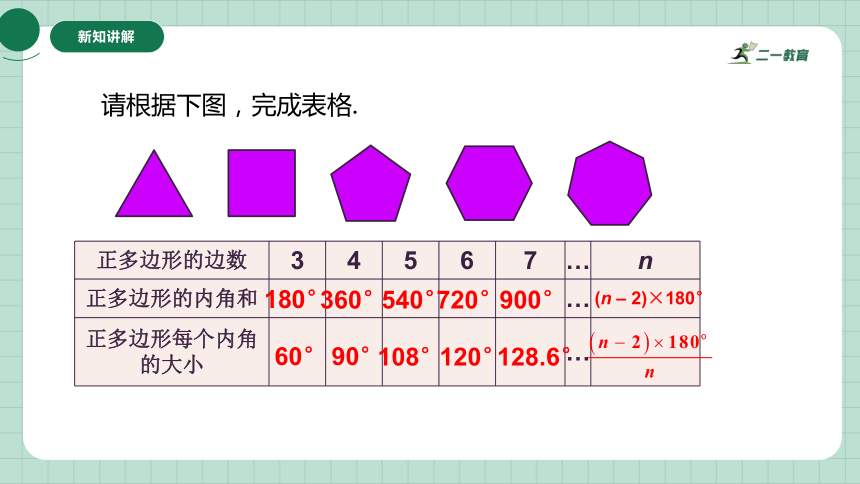
请根据下图,完成表格.
正多边形的边数 3 4 5 6 7 … n
正多边形的内角和 …
正多边形每个内角的大小 …
180°
60°
360°
90°
540°
108°
720°
120°
900°
128.6°
(n – 2)×180°
新知讲解
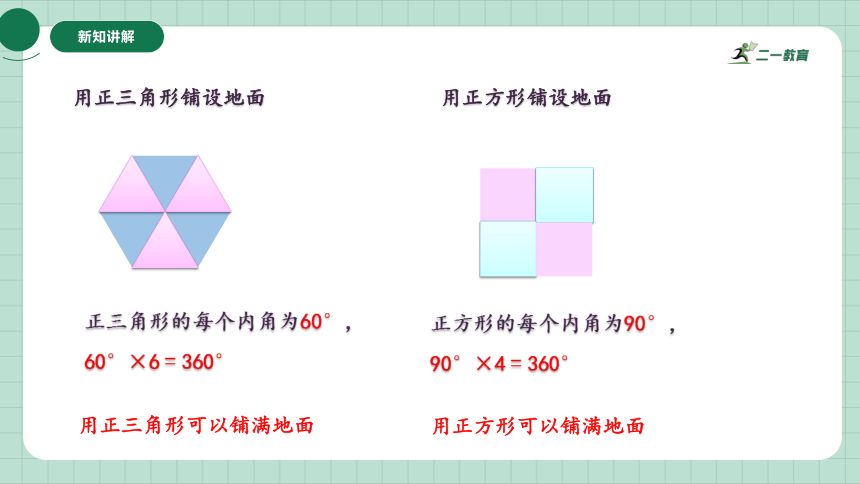
用正三角形铺设地面
正三角形的每个内角为60,
60×6 = 360
用正三角形可以铺满地面
用正方形铺设地面
正方形的每个内角为90,
90×4 = 360
用正方形可以铺满地面
新知讲解
用正五边形铺设地面
正五边形的每个内角为108,
108×3 = 324
用正五边形不能铺满地面
用正六边形铺设地面
正六边形的每个内角为120,
120×3 = 360
用正六边形可以铺满地面
新知讲解
概括:
使用给定的某种正多边形,当围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面.
如果用 x 表示正多边形的一个内角的度数,a 表示正多边形的个数,那么上面的结论可表示为:
ax = 360°
新知讲解
正三角形、正方形、正六边形两两结合是否能够铺满地面呢?把正三角形、正方形、正六边形三者结合在一起呢?
120°+120°+60°+60°=360°
用正三角形和正六边形能铺满地面
新知讲解
120°+90°+90°+60°=360°
用正三角形、正方形和正六边形能铺满地面
使用给定的某种正多边形,当围绕一点拼在一起的几个内角加在一起恰好组成一个周角(360°)时,就可以铺满地面.
设每一个公共顶点不同的正多边形分别有 m 个、n 个、···,正多边形的一个内角度数分别为 α、β、···,若几种正多边形组合起来能铺板地面,则:
mα + nβ + ··· = 360°
【知识技能类作业】必做题:
课堂练习
1.学校科技馆的地面准备铺设一些边长相同的正六边形地砖,那么在每一个顶点处,应铺设( )
A.2块 B.3块 C.4块 D.5块
B
【知识技能类作业】必做题:
课堂练习
2.在下列正多边形组合中,不能铺满地面的是( )
A.正八边形和正方形 B.正五边形和正八边形
C.正六边形和正三角形 D.正三角形和正方形
B
【知识技能类作业】必做题:
课堂练习
3.如果在正三角形、正方形、正六边形、正十二边形这四种形状的地砖中,任意选择其中三种密铺,有几种可行的方案?
解:正三角形、正方形,正十二边形可以密铺;
正方形,正六边形,正十二边形可以密铺;
正三角形,正方形,正六边形可以密铺.
故有3种可行的方案.
【知识技能类作业】选做题:
课堂练习
4.有一种正多边形地砖的每个内角都是150°,则下列能与其组合铺满地面的地砖的形状是( )
A. 正三角形 B. 正四边形 C. 正五边形 D. 正六边形
A
5. 某休闲广场的地面中间是1块正六边形地砖,周围是用正方形地砖和正三角形地砖按如图所示的方式依次向外铺设10圈而成的,其中第1圈有6块正方形地砖和6块正三角形地砖,则铺设该广场共用 块地砖.
【知识技能类作业】选做题:
课堂练习
661
【综合拓展类作业】
课堂练习
6. 现有边长相等的正三角形、正方形和正六边形三种瓷砖若干块,要求:① 三种瓷砖都必须用到;② 铺成长方形或近似长方形.请你设计一种密铺方案并画出来(瓷砖可切割).
解:答案不唯一,如图所示,
∵ 正三角形、正方形、正六边形的每个内角分别为60°、90°、120°,且60°×1+90°×2+120°×1=360°,∴ 每一个顶点处铺1块正三角形瓷砖,2块正方形瓷砖,1块正六边形瓷砖即可.
课堂总结
1.用相同的正多边形铺设地面:
围绕一点拼在一起的几个内角加在一起恰好组成一个周角.
2.用多种正多边形铺设地面:
围绕一点拼在一起的多种正多边形的内角之和为360 .
板书设计
1.用相同的正多边形铺设地面:
围绕一点拼在一起的几个内角加在一起恰好组成一个周角.
2.用多种正多边形铺设地面:
围绕一点拼在一起的多种正多边形的内角之和为360 .
课题:8.3用正多边形铺设地面
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
(华师大版)七年级
下
8.3用正多边形铺设地面
三角形
第8章
“八”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.通过用相同的正多边形铺地面的活动,巩固多边形的内角和与外角和公式;
2.通过“铺地面”和相关计算,使学生从中发现能拼成一个不留空隙,又不重叠的平面图形的关键是几个多边形的内角和相加要等于360°.
新知导入
问题1:多边形的内角和、外角和.
n 边形的内角和为(n2)×180°,外角和为360°.
问题2:正多边形的一个内角和一个外角怎样计算?
正 n 边形的一个内角为,一个外角为.
新知导入
思考:这些地砖都是什么形状?为什么能铺满地面而不留一点空隙呢?换一些其他形状的行不行?
新知讲解
围绕某一顶点铺满地面
生活中常常用瓷砖严丝合缝、不留空隙地铺满墙面或地面. 从数学的角度看,就是用几何图形不留空隙、不重叠地铺满平面的一部分,这就是平面图形的镶嵌.
新知讲解
使用给定的某种正多边形,它能否铺满地面,既不留下一丝空白,又不互相重叠呢?
与正多边形的内角大小有关
新知讲解
请根据下图,完成表格.
正多边形的边数 3 4 5 6 7 … n
正多边形的内角和 …
正多边形每个内角的大小 …
180°
60°
360°
90°
540°
108°
720°
120°
900°
128.6°
(n – 2)×180°
新知讲解
用正三角形铺设地面
正三角形的每个内角为60,
60×6 = 360
用正三角形可以铺满地面
用正方形铺设地面
正方形的每个内角为90,
90×4 = 360
用正方形可以铺满地面
新知讲解
用正五边形铺设地面
正五边形的每个内角为108,
108×3 = 324
用正五边形不能铺满地面
用正六边形铺设地面
正六边形的每个内角为120,
120×3 = 360
用正六边形可以铺满地面
新知讲解
概括:
使用给定的某种正多边形,当围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面.
如果用 x 表示正多边形的一个内角的度数,a 表示正多边形的个数,那么上面的结论可表示为:
ax = 360°
新知讲解
正三角形、正方形、正六边形两两结合是否能够铺满地面呢?把正三角形、正方形、正六边形三者结合在一起呢?
120°+120°+60°+60°=360°
用正三角形和正六边形能铺满地面
新知讲解
120°+90°+90°+60°=360°
用正三角形、正方形和正六边形能铺满地面
使用给定的某种正多边形,当围绕一点拼在一起的几个内角加在一起恰好组成一个周角(360°)时,就可以铺满地面.
设每一个公共顶点不同的正多边形分别有 m 个、n 个、···,正多边形的一个内角度数分别为 α、β、···,若几种正多边形组合起来能铺板地面,则:
mα + nβ + ··· = 360°
【知识技能类作业】必做题:
课堂练习
1.学校科技馆的地面准备铺设一些边长相同的正六边形地砖,那么在每一个顶点处,应铺设( )
A.2块 B.3块 C.4块 D.5块
B
【知识技能类作业】必做题:
课堂练习
2.在下列正多边形组合中,不能铺满地面的是( )
A.正八边形和正方形 B.正五边形和正八边形
C.正六边形和正三角形 D.正三角形和正方形
B
【知识技能类作业】必做题:
课堂练习
3.如果在正三角形、正方形、正六边形、正十二边形这四种形状的地砖中,任意选择其中三种密铺,有几种可行的方案?
解:正三角形、正方形,正十二边形可以密铺;
正方形,正六边形,正十二边形可以密铺;
正三角形,正方形,正六边形可以密铺.
故有3种可行的方案.
【知识技能类作业】选做题:
课堂练习
4.有一种正多边形地砖的每个内角都是150°,则下列能与其组合铺满地面的地砖的形状是( )
A. 正三角形 B. 正四边形 C. 正五边形 D. 正六边形
A
5. 某休闲广场的地面中间是1块正六边形地砖,周围是用正方形地砖和正三角形地砖按如图所示的方式依次向外铺设10圈而成的,其中第1圈有6块正方形地砖和6块正三角形地砖,则铺设该广场共用 块地砖.
【知识技能类作业】选做题:
课堂练习
661
【综合拓展类作业】
课堂练习
6. 现有边长相等的正三角形、正方形和正六边形三种瓷砖若干块,要求:① 三种瓷砖都必须用到;② 铺成长方形或近似长方形.请你设计一种密铺方案并画出来(瓷砖可切割).
解:答案不唯一,如图所示,
∵ 正三角形、正方形、正六边形的每个内角分别为60°、90°、120°,且60°×1+90°×2+120°×1=360°,∴ 每一个顶点处铺1块正三角形瓷砖,2块正方形瓷砖,1块正六边形瓷砖即可.
课堂总结
1.用相同的正多边形铺设地面:
围绕一点拼在一起的几个内角加在一起恰好组成一个周角.
2.用多种正多边形铺设地面:
围绕一点拼在一起的多种正多边形的内角之和为360 .
板书设计
1.用相同的正多边形铺设地面:
围绕一点拼在一起的几个内角加在一起恰好组成一个周角.
2.用多种正多边形铺设地面:
围绕一点拼在一起的多种正多边形的内角之和为360 .
课题:8.3用正多边形铺设地面
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
