8.2多边形的内角和与外角和(第1课时)课件(共33张PPT)
文档属性
| 名称 | 8.2多边形的内角和与外角和(第1课时)课件(共33张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 00:00:00 | ||
图片预览




文档简介
(共33张PPT)
(华师大版)七年级
下
8.2多边形的内角和与外角和(第1课时)
三角形
第8章
“八”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.理解多边形及多边形的内角等概念;
2.掌握多边形的内角和公式;
3.经历把多边形转化为三角形的过程,体会转化思想.
新知导入
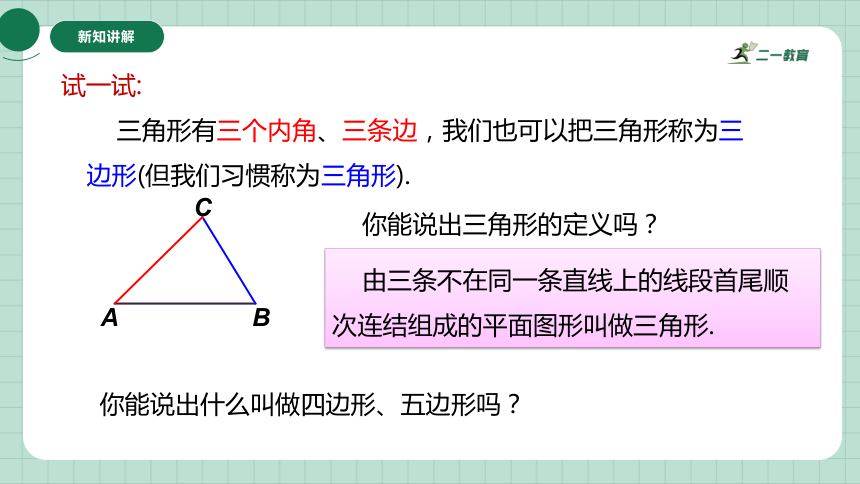
在实际生活当中,除了三角形,还有许多由线段围成的图形.观察图片,你能找到由一些线段围成的图形吗?
新知导入
中国某一村远景图
五角大楼
新知讲解
试一试:
由三条不在同一条直线上的线段首尾顺次连结组成的平面图形叫做三角形.
你能说出什么叫做四边形、五边形吗?
C
A
B
三角形有三个内角、三条边,我们也可以把三角形称为三边形(但我们习惯称为三角形).
你能说出三角形的定义吗?
新知讲解
A
B
D
C
①
A
B
D
C
②
E
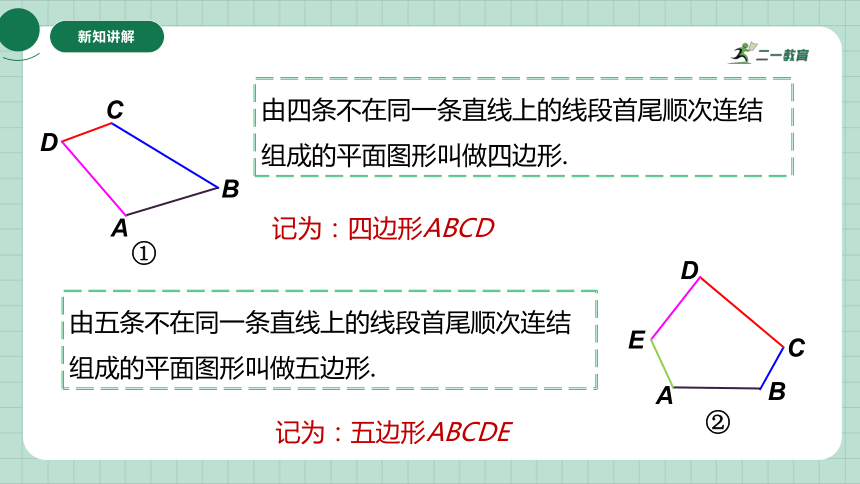
由四条不在同一条直线上的线段首尾顺次连结组成的平面图形叫做四边形.
由五条不在同一条直线上的线段首尾顺次连结组成的平面图形叫做五边形.
记为:四边形ABCD
记为:五边形ABCDE
新知讲解
概括:
一般地,由n条不在同一条直线上的线段首尾顺次连结组成的平面图形称为n边形,也即我们通常所说的多边形.
多边形用图形名称以及它的各个顶点的字母表示.
字母要按照顶点的顺序书写,可以按顺时针或逆时针的顺序.
新知讲解
A
D
C
B
A
C
B
D
①
②
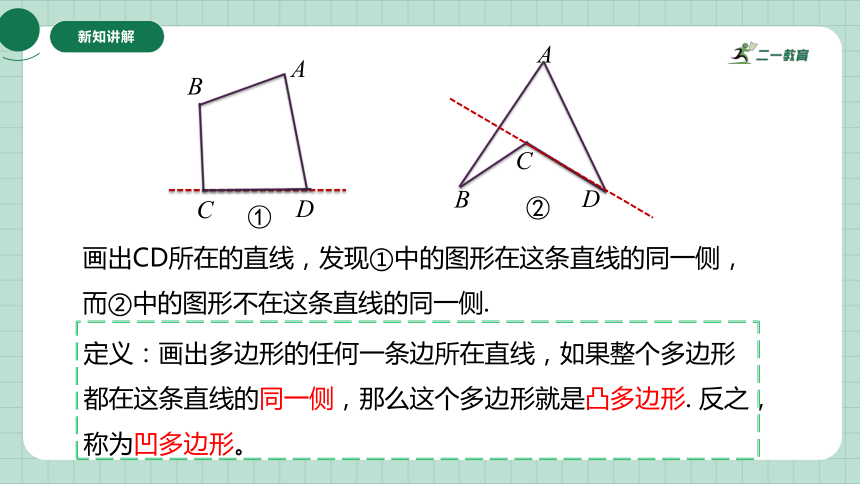
画出CD所在的直线,发现①中的图形在这条直线的同一侧,而②中的图形不在这条直线的同一侧.
定义:画出多边形的任何一条边所在直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形. 反之,称为凹多边形。
新知讲解
B
F
E
A
D
C
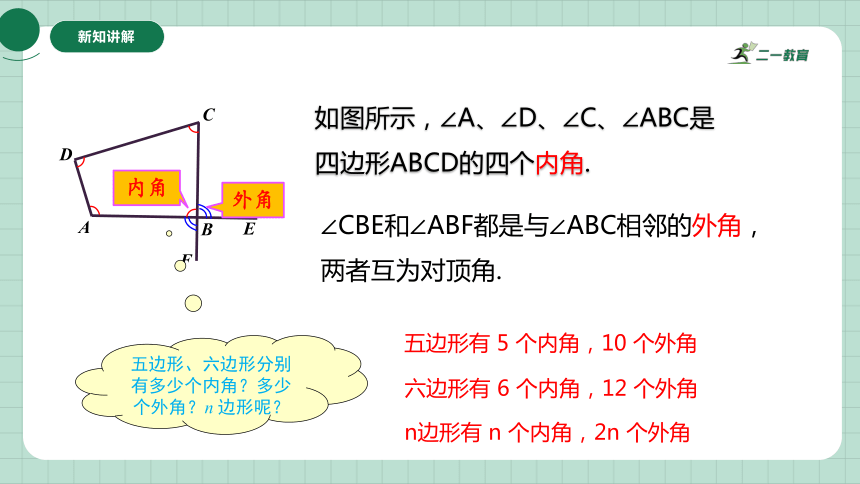
如图所示,∠A、∠D、∠C、∠ABC是四边形ABCD的四个内角.
∠CBE和∠ABF都是与∠ABC相邻的外角,两者互为对顶角.
外角
内角
五边形、六边形分别有多少个内角?多少个外角?n 边形呢?
五边形有 5 个内角,10 个外角
六边形有 6 个内角,12 个外角
n边形有 n 个内角,2n 个外角
新知讲解
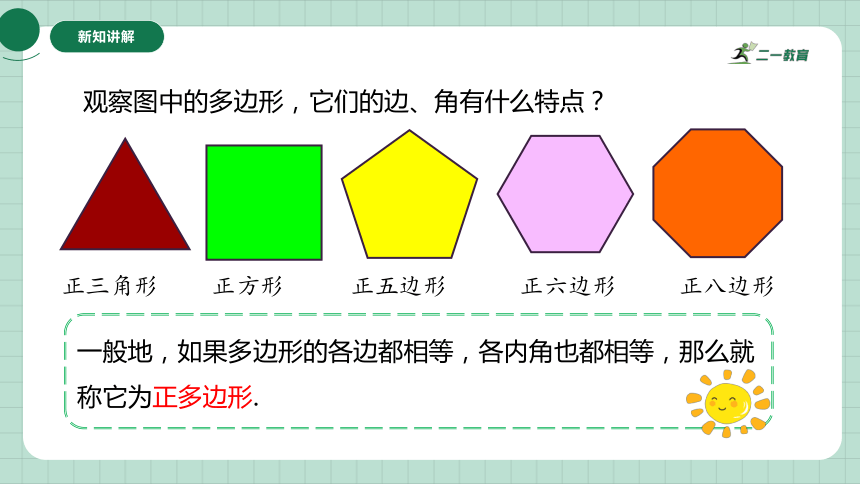
观察图中的多边形,它们的边、角有什么特点?
正方形
正五边形
正六边形
正三角形
正八边形
一般地,如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.
新知讲解
概括:
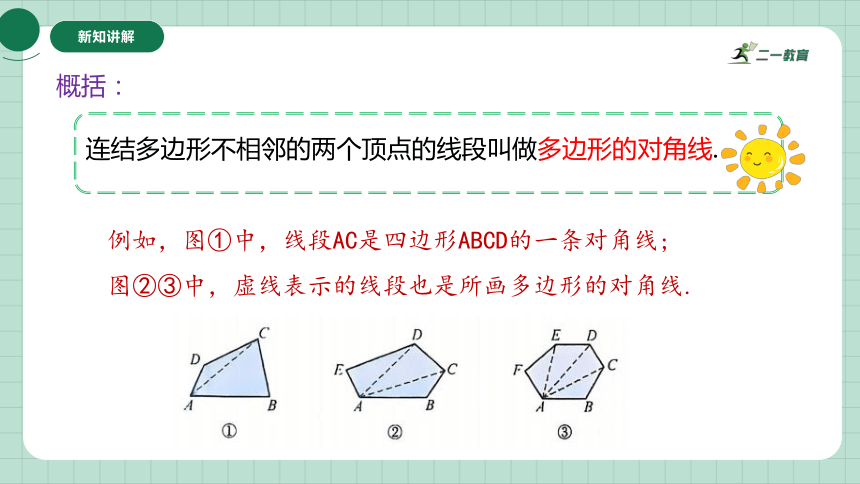
连结多边形不相邻的两个顶点的线段叫做多边形的对角线.
例如,图①中,线段AC是四边形ABCD的一条对角线;
图②③中,虚线表示的线段也是所画多边形的对角线.
新知讲解
三角形
六边形
四边形
八边形
……
五边形
请画出下列图形从某一顶点出发的对角线的条数:
多边形 三角形 四边形 五边形 六边形 八边形 n边形
从同一顶点引出的对角线的条数
分割出的三角形的个数
0
1
2
3
5
n-3
1
2
3
4
6
n-2
新知讲解
从n(n≥3)边形的一个顶点可以作出(n-3)条对角线.
将多边形分成(n-2)个三角形.
n(n≥3)边形共有对角线 条.
新知讲解
试一试:
由图中可以看出,从多边形的一个顶点引出的对角线把多边形划分为若干个三角形.
内角和 = 180°
内角和 = ?
新知讲解
为了求得 n 边形的内角和,请根据下图,完成表格.
多边形的边数 3 4 5 6 7 … n
分成的三角形个数 1 2 …
多边形的内角和 180° …
540°
3
4
720°
5
900°
n – 2
(n – 2)·180°
360°
由此,我们得出 n 边形的内角和等于
(n – 2)·180°(n≥3,n为正整数)
新知讲解
想一想,对于正多边形来说,又有怎样的结论呢?
因为正多边形的每个角相等,所以知道正多边形的边数,就可以求出每一个内角的度数.
正 n 边形的每个内角度数:
新知讲解
“归纳推理”是数学中的一种推理方式,体现了从特殊到一般的推理过程. 在这里,我们通过对三边形、四边形、五边形等的探索,发现它们的内角和与边数之间存在某种逻辑关系,从而归纳出多边形的内角和公式. 这种归纳推理的方式,我们今后还会经常用到. 当然,“看”出来的数学结论未必一定正确,但它们还是给我们指引了研究的方向. 因此,归纳推理和演绎推理相结合是必要的.
读
一
读
新知讲解
例1 求八边形的内角和.
解:八边形的内角和为
(n-2)×180=(8-2)×180= 1 080°.
新知讲解
例2 已知一个多边形的内角和等于2160°,求这个多边形的边数.
解:设这个多边形的边数为n,根据题意,得
(n-2).180°=2160°.
解得 n=14.
因此,这个多边形的边数为14.
新知讲解
如图,在 n 边形(图中取 n = 6 的情形)内任取一点 P,连结点 P 与多边形的每一个顶点,可得到几个三角形?你能否根据这样划分多边形的方法来说明 n 边形的内角和等于(n2)·180°?
P
n·180°360°=(n2)·180°
还有其他方法能说明多边形的内角和公式吗?
n 边形有 n 个顶点,可得到 n 个三角形
试一试:
新知讲解
P
点 P 在某一条边上时:
划分成(n2)个三角形,
n 边形的内角和为(n2)·180°
思考:这种方法与前面两种方法有何共同点?
都是把多边形分成若干个三角形
其他方法:
【知识技能类作业】必做题:
课堂练习
1.在如图所示的图形中,属于多边形的有( )
A.2个 B.3个 C.4个 D.5个
B
【知识技能类作业】必做题:
课堂练习
2.从多边形的一个顶点出发的对角线一共有6条,则这个多边形是( )
A.六边形 B.七边形 C.八边形 D.九边形
D
【知识技能类作业】必做题:
课堂练习
3. 在四边形ABCD中,∠A∶∠B=5∶7,∠B-∠A=∠C,∠D-∠C=80°,求这个四边形的四个内角的度数.
解:设∠A=(5x)°,则∠B=(7x)°,∠C=(2x)°,∠D=(2x+80)°.
根据四边形的内角和为360°,得(5x)°+(7x)°+(2x)°+(2x+80)°=360°,
解得x=17.5.
∴ ∠A=87.5°,∠B=122.5°,∠C=35°,∠D=115°
【知识技能类作业】选做题:
课堂练习
4.下列度数不是多边形的内角和的为( )
A. 540° B. 600° C. 900° D. 1980°
B
5. 如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是( )
A. 50° B. 55° C. 60° D. 65°
【知识技能类作业】选做题:
课堂练习
C
【综合拓展类作业】
课堂练习
6. 小丽进行多边形内角和的计算时,求得一多边形的内角和为1500°,当她发现错了之后,重新检查,发现少加了一个内角.你知道她少加的这个内角的度数是多少吗 她求的这个多边形是几边形
解:设小丽少加的这个内角的度数是x,多边形的边数为n.
由题意,得(n-2)×180°=1500°+x,即(n-2)×180°=8×180°+60°+x.
∵ 等式两边都是180°的整数倍,且0°∴ 她少加的这个内角的度数是120°,求的这个多边形是十一边形
课堂总结
1.多边形:
一般地,由n条不在同一条直线上的线段首尾顺次连结组成的平面图形称为n边形,也即我们通常所说的多边形.
2.多边形的对角线:
连结多边形不相邻的两个顶点的线段叫做多边形的对角线.
从n(n≥3)边形的一个顶点可以作出(n-3)条对角线.
将多边形分成(n-2)个三角形.
n(n≥3)边形共有对角线 条.
课堂总结
3.多边形的内角和:
n 边形的内角和等于
(n – 2)·180°(n≥3,n为正整数)
正 n 边形的每个内角度数:
板书设计
1.多边形及其相关定义:
2.多边形的对角线:
3.多边形的内角和:
课题:8.2多边形的内角和与外角和(第1课时)
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
(华师大版)七年级
下
8.2多边形的内角和与外角和(第1课时)
三角形
第8章
“八”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.理解多边形及多边形的内角等概念;
2.掌握多边形的内角和公式;
3.经历把多边形转化为三角形的过程,体会转化思想.
新知导入
在实际生活当中,除了三角形,还有许多由线段围成的图形.观察图片,你能找到由一些线段围成的图形吗?
新知导入
中国某一村远景图
五角大楼
新知讲解
试一试:
由三条不在同一条直线上的线段首尾顺次连结组成的平面图形叫做三角形.
你能说出什么叫做四边形、五边形吗?
C
A
B
三角形有三个内角、三条边,我们也可以把三角形称为三边形(但我们习惯称为三角形).
你能说出三角形的定义吗?
新知讲解
A
B
D
C
①
A
B
D
C
②
E
由四条不在同一条直线上的线段首尾顺次连结组成的平面图形叫做四边形.
由五条不在同一条直线上的线段首尾顺次连结组成的平面图形叫做五边形.
记为:四边形ABCD
记为:五边形ABCDE
新知讲解
概括:
一般地,由n条不在同一条直线上的线段首尾顺次连结组成的平面图形称为n边形,也即我们通常所说的多边形.
多边形用图形名称以及它的各个顶点的字母表示.
字母要按照顶点的顺序书写,可以按顺时针或逆时针的顺序.
新知讲解
A
D
C
B
A
C
B
D
①
②
画出CD所在的直线,发现①中的图形在这条直线的同一侧,而②中的图形不在这条直线的同一侧.
定义:画出多边形的任何一条边所在直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形. 反之,称为凹多边形。
新知讲解
B
F
E
A
D
C
如图所示,∠A、∠D、∠C、∠ABC是四边形ABCD的四个内角.
∠CBE和∠ABF都是与∠ABC相邻的外角,两者互为对顶角.
外角
内角
五边形、六边形分别有多少个内角?多少个外角?n 边形呢?
五边形有 5 个内角,10 个外角
六边形有 6 个内角,12 个外角
n边形有 n 个内角,2n 个外角
新知讲解
观察图中的多边形,它们的边、角有什么特点?
正方形
正五边形
正六边形
正三角形
正八边形
一般地,如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.
新知讲解
概括:
连结多边形不相邻的两个顶点的线段叫做多边形的对角线.
例如,图①中,线段AC是四边形ABCD的一条对角线;
图②③中,虚线表示的线段也是所画多边形的对角线.
新知讲解
三角形
六边形
四边形
八边形
……
五边形
请画出下列图形从某一顶点出发的对角线的条数:
多边形 三角形 四边形 五边形 六边形 八边形 n边形
从同一顶点引出的对角线的条数
分割出的三角形的个数
0
1
2
3
5
n-3
1
2
3
4
6
n-2
新知讲解
从n(n≥3)边形的一个顶点可以作出(n-3)条对角线.
将多边形分成(n-2)个三角形.
n(n≥3)边形共有对角线 条.
新知讲解
试一试:
由图中可以看出,从多边形的一个顶点引出的对角线把多边形划分为若干个三角形.
内角和 = 180°
内角和 = ?
新知讲解
为了求得 n 边形的内角和,请根据下图,完成表格.
多边形的边数 3 4 5 6 7 … n
分成的三角形个数 1 2 …
多边形的内角和 180° …
540°
3
4
720°
5
900°
n – 2
(n – 2)·180°
360°
由此,我们得出 n 边形的内角和等于
(n – 2)·180°(n≥3,n为正整数)
新知讲解
想一想,对于正多边形来说,又有怎样的结论呢?
因为正多边形的每个角相等,所以知道正多边形的边数,就可以求出每一个内角的度数.
正 n 边形的每个内角度数:
新知讲解
“归纳推理”是数学中的一种推理方式,体现了从特殊到一般的推理过程. 在这里,我们通过对三边形、四边形、五边形等的探索,发现它们的内角和与边数之间存在某种逻辑关系,从而归纳出多边形的内角和公式. 这种归纳推理的方式,我们今后还会经常用到. 当然,“看”出来的数学结论未必一定正确,但它们还是给我们指引了研究的方向. 因此,归纳推理和演绎推理相结合是必要的.
读
一
读
新知讲解
例1 求八边形的内角和.
解:八边形的内角和为
(n-2)×180=(8-2)×180= 1 080°.
新知讲解
例2 已知一个多边形的内角和等于2160°,求这个多边形的边数.
解:设这个多边形的边数为n,根据题意,得
(n-2).180°=2160°.
解得 n=14.
因此,这个多边形的边数为14.
新知讲解
如图,在 n 边形(图中取 n = 6 的情形)内任取一点 P,连结点 P 与多边形的每一个顶点,可得到几个三角形?你能否根据这样划分多边形的方法来说明 n 边形的内角和等于(n2)·180°?
P
n·180°360°=(n2)·180°
还有其他方法能说明多边形的内角和公式吗?
n 边形有 n 个顶点,可得到 n 个三角形
试一试:
新知讲解
P
点 P 在某一条边上时:
划分成(n2)个三角形,
n 边形的内角和为(n2)·180°
思考:这种方法与前面两种方法有何共同点?
都是把多边形分成若干个三角形
其他方法:
【知识技能类作业】必做题:
课堂练习
1.在如图所示的图形中,属于多边形的有( )
A.2个 B.3个 C.4个 D.5个
B
【知识技能类作业】必做题:
课堂练习
2.从多边形的一个顶点出发的对角线一共有6条,则这个多边形是( )
A.六边形 B.七边形 C.八边形 D.九边形
D
【知识技能类作业】必做题:
课堂练习
3. 在四边形ABCD中,∠A∶∠B=5∶7,∠B-∠A=∠C,∠D-∠C=80°,求这个四边形的四个内角的度数.
解:设∠A=(5x)°,则∠B=(7x)°,∠C=(2x)°,∠D=(2x+80)°.
根据四边形的内角和为360°,得(5x)°+(7x)°+(2x)°+(2x+80)°=360°,
解得x=17.5.
∴ ∠A=87.5°,∠B=122.5°,∠C=35°,∠D=115°
【知识技能类作业】选做题:
课堂练习
4.下列度数不是多边形的内角和的为( )
A. 540° B. 600° C. 900° D. 1980°
B
5. 如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是( )
A. 50° B. 55° C. 60° D. 65°
【知识技能类作业】选做题:
课堂练习
C
【综合拓展类作业】
课堂练习
6. 小丽进行多边形内角和的计算时,求得一多边形的内角和为1500°,当她发现错了之后,重新检查,发现少加了一个内角.你知道她少加的这个内角的度数是多少吗 她求的这个多边形是几边形
解:设小丽少加的这个内角的度数是x,多边形的边数为n.
由题意,得(n-2)×180°=1500°+x,即(n-2)×180°=8×180°+60°+x.
∵ 等式两边都是180°的整数倍,且0°
课堂总结
1.多边形:
一般地,由n条不在同一条直线上的线段首尾顺次连结组成的平面图形称为n边形,也即我们通常所说的多边形.
2.多边形的对角线:
连结多边形不相邻的两个顶点的线段叫做多边形的对角线.
从n(n≥3)边形的一个顶点可以作出(n-3)条对角线.
将多边形分成(n-2)个三角形.
n(n≥3)边形共有对角线 条.
课堂总结
3.多边形的内角和:
n 边形的内角和等于
(n – 2)·180°(n≥3,n为正整数)
正 n 边形的每个内角度数:
板书设计
1.多边形及其相关定义:
2.多边形的对角线:
3.多边形的内角和:
课题:8.2多边形的内角和与外角和(第1课时)
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
