8.2 多边形的内角和与外角和(第2课时) 课件(共20张PPT)
文档属性
| 名称 | 8.2 多边形的内角和与外角和(第2课时) 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 663.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
(华师大版)七年级
下
8.2多边形的内角和与外角和(第2课时)
三角形
第8章
“八”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.掌握多边形外角和定理;
2.能应用多边形的外角和解决问题.
新知导入
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
用形状、大小完全相同的任意四边形可拼成一块无空隙的地板,你知道这是为什么吗?
新知讲解
1
2
3
4
5
6
7
8
C
B
D
A
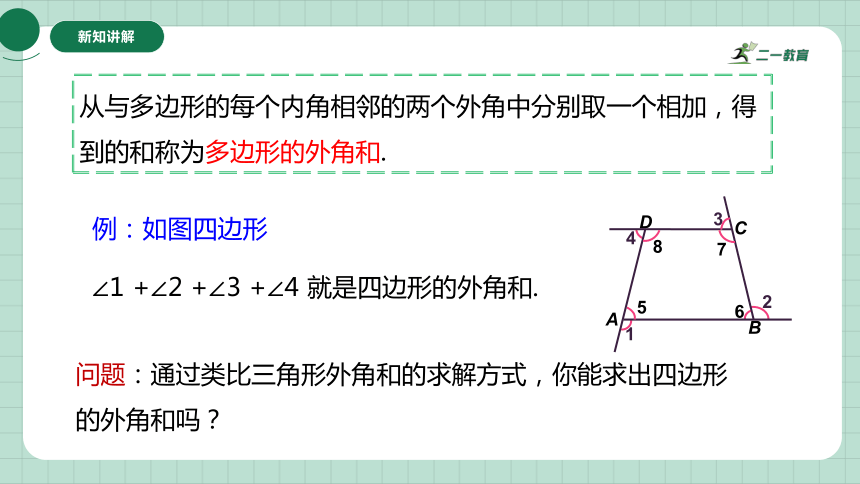
例:如图四边形
∠1 +∠2 +∠3 +∠4 就是四边形的外角和.
从与多边形的每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和.
问题:通过类比三角形外角和的求解方式,你能求出四边形的外角和吗?
新知讲解
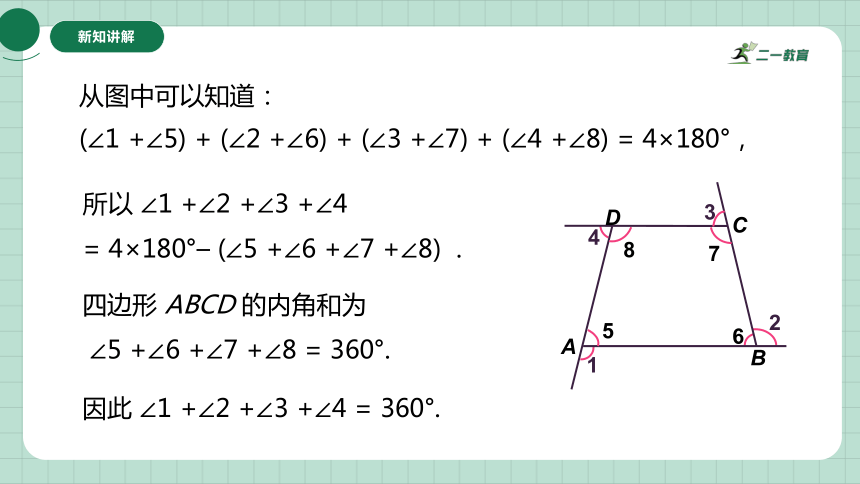
从图中可以知道:
(∠1 +∠5) + (∠2 +∠6) + (∠3 +∠7) + (∠4 +∠8) = 4×180°,
所以 ∠1 +∠2 +∠3 +∠4
= 4×180°– (∠5 +∠6 +∠7 +∠8) .
四边形 ABCD 的内角和为
∠5 +∠6 +∠7 +∠8 = 360°.
因此 ∠1 +∠2 +∠3 +∠4 = 360°.
1
2
3
4
5
6
7
8
C
B
D
A
思考:
新知讲解
根据 n 边形的每一个内角与和它相邻的外角都互为补角,可以求得 n 边形的外角和. 据此,请将数据填入表格.
多边形的边数 3 4 5 6 7 n
多边形的内角和与外角和的总和
多边形的内角和
多边形的外角和
n×180°
(n-2)×180°
540°
180°
360°
360°
360°
360°
360°
360°
720°
360°
900°
540°
1 080°
720°
1 260°
900°
任意多边形的外角和都为 360°.
新知讲解
例3 一个多边形的每个外角都是72°,这个多边形是几边形
解:设这个多边形的边数为n,根据题意,得 n 72°=360°.
解得 n =5.
因此,这个多边形是五边形.
新知讲解
例4 一个多边形的内角和等于它外角和的5倍,这个多边形是几边形
解:设这个多边形的边数为n,根据题意,得 (n-2)·180°=5x 360°.
解得 n=12.
因此,这个多边形是十二边形.
新知讲解
思考:正多边形的每个外角是多少度?
因为正多边形的每个角相等,所以知道正多边形的边数,就可以求出每一个外角的度数.
正 n 边形的每个外角度数:
【知识技能类作业】必做题:
课堂练习
1.已知一个多边形的每个外角都等于 ,则该多边形的边数是( )
A.4 B.5 C.6 D.7
C
【知识技能类作业】必做题:
课堂练习
2.如图,小明和小丽分别在四边形和六边形的人工湖边散步,两人各走完一圈后发现两人转过的角度相同,能够解释这一现象的是( )
A.多边形的内角和与边数无关,为定值
B.多边形的内角和与边数有关
C.多边形的外角和与边数无关,为定值
D.以上都不对
C
【知识技能类作业】必做题:
课堂练习
3.一个多边形内角和的度数比外角和的度数的4倍多 ,求这个多边
形的边数.
解:设多边形的边数为 ,
由题意,得 ,解得 ,
所以这个多边形的边数为11.
【知识技能类作业】选做题:
课堂练习
4.若一个正多边形的一个内角比与它相邻的外角大108°,则这个正多边形的内角和为( )
A. 1080° B. 1260° C. 1440° D. 1800°
C
5. 如图,在五边形ABCDE中,AB∥ED,∠1、∠2、∠3分别是它的外角,则∠1+∠2+∠3的度数为( )
A. 180° B. 210° C. 240° D. 270°
【知识技能类作业】选做题:
课堂练习
A
【综合拓展类作业】
课堂练习
6. 如图,在七边形ABCDEFG中,AB、ED的延长线相交于点O.若∠1、∠2、∠3、∠4的邻补角的度数和为220°,求∠BOD的度数.
解:∵ ∠1、∠2、∠3、∠4的邻补角的度数和为220°,
∴ ∠1+∠2+∠3+∠4=180°×4-220°=500°.
∵ 五边形OAGFE的内角和为(5-2)×180°=540°,
∴ ∠BOD=540°-(∠1+∠2+∠3+∠4)=540°-500°=40°
课堂总结
1.多边形的外角和定义:
从与多边形的每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和.
2.任意多边形的外角和都为 360°.
正 n 边形的每个外角度数:
板书设计
1.多边形的外角和定义:
2.多边形的外角和:
课题:8.2多边形的内角和与外角和(第2课时)
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
(华师大版)七年级
下
8.2多边形的内角和与外角和(第2课时)
三角形
第8章
“八”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.掌握多边形外角和定理;
2.能应用多边形的外角和解决问题.
新知导入
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2
4
1
3
用形状、大小完全相同的任意四边形可拼成一块无空隙的地板,你知道这是为什么吗?
新知讲解
1
2
3
4
5
6
7
8
C
B
D
A
例:如图四边形
∠1 +∠2 +∠3 +∠4 就是四边形的外角和.
从与多边形的每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和.
问题:通过类比三角形外角和的求解方式,你能求出四边形的外角和吗?
新知讲解
从图中可以知道:
(∠1 +∠5) + (∠2 +∠6) + (∠3 +∠7) + (∠4 +∠8) = 4×180°,
所以 ∠1 +∠2 +∠3 +∠4
= 4×180°– (∠5 +∠6 +∠7 +∠8) .
四边形 ABCD 的内角和为
∠5 +∠6 +∠7 +∠8 = 360°.
因此 ∠1 +∠2 +∠3 +∠4 = 360°.
1
2
3
4
5
6
7
8
C
B
D
A
思考:
新知讲解
根据 n 边形的每一个内角与和它相邻的外角都互为补角,可以求得 n 边形的外角和. 据此,请将数据填入表格.
多边形的边数 3 4 5 6 7 n
多边形的内角和与外角和的总和
多边形的内角和
多边形的外角和
n×180°
(n-2)×180°
540°
180°
360°
360°
360°
360°
360°
360°
720°
360°
900°
540°
1 080°
720°
1 260°
900°
任意多边形的外角和都为 360°.
新知讲解
例3 一个多边形的每个外角都是72°,这个多边形是几边形
解:设这个多边形的边数为n,根据题意,得 n 72°=360°.
解得 n =5.
因此,这个多边形是五边形.
新知讲解
例4 一个多边形的内角和等于它外角和的5倍,这个多边形是几边形
解:设这个多边形的边数为n,根据题意,得 (n-2)·180°=5x 360°.
解得 n=12.
因此,这个多边形是十二边形.
新知讲解
思考:正多边形的每个外角是多少度?
因为正多边形的每个角相等,所以知道正多边形的边数,就可以求出每一个外角的度数.
正 n 边形的每个外角度数:
【知识技能类作业】必做题:
课堂练习
1.已知一个多边形的每个外角都等于 ,则该多边形的边数是( )
A.4 B.5 C.6 D.7
C
【知识技能类作业】必做题:
课堂练习
2.如图,小明和小丽分别在四边形和六边形的人工湖边散步,两人各走完一圈后发现两人转过的角度相同,能够解释这一现象的是( )
A.多边形的内角和与边数无关,为定值
B.多边形的内角和与边数有关
C.多边形的外角和与边数无关,为定值
D.以上都不对
C
【知识技能类作业】必做题:
课堂练习
3.一个多边形内角和的度数比外角和的度数的4倍多 ,求这个多边
形的边数.
解:设多边形的边数为 ,
由题意,得 ,解得 ,
所以这个多边形的边数为11.
【知识技能类作业】选做题:
课堂练习
4.若一个正多边形的一个内角比与它相邻的外角大108°,则这个正多边形的内角和为( )
A. 1080° B. 1260° C. 1440° D. 1800°
C
5. 如图,在五边形ABCDE中,AB∥ED,∠1、∠2、∠3分别是它的外角,则∠1+∠2+∠3的度数为( )
A. 180° B. 210° C. 240° D. 270°
【知识技能类作业】选做题:
课堂练习
A
【综合拓展类作业】
课堂练习
6. 如图,在七边形ABCDEFG中,AB、ED的延长线相交于点O.若∠1、∠2、∠3、∠4的邻补角的度数和为220°,求∠BOD的度数.
解:∵ ∠1、∠2、∠3、∠4的邻补角的度数和为220°,
∴ ∠1+∠2+∠3+∠4=180°×4-220°=500°.
∵ 五边形OAGFE的内角和为(5-2)×180°=540°,
∴ ∠BOD=540°-(∠1+∠2+∠3+∠4)=540°-500°=40°
课堂总结
1.多边形的外角和定义:
从与多边形的每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和.
2.任意多边形的外角和都为 360°.
正 n 边形的每个外角度数:
板书设计
1.多边形的外角和定义:
2.多边形的外角和:
课题:8.2多边形的内角和与外角和(第2课时)
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
