2021年广东省中考数学试卷学生版(无答案)
文档属性
| 名称 | 2021年广东省中考数学试卷学生版(无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 84.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-22 00:00:00 | ||
图片预览


文档简介
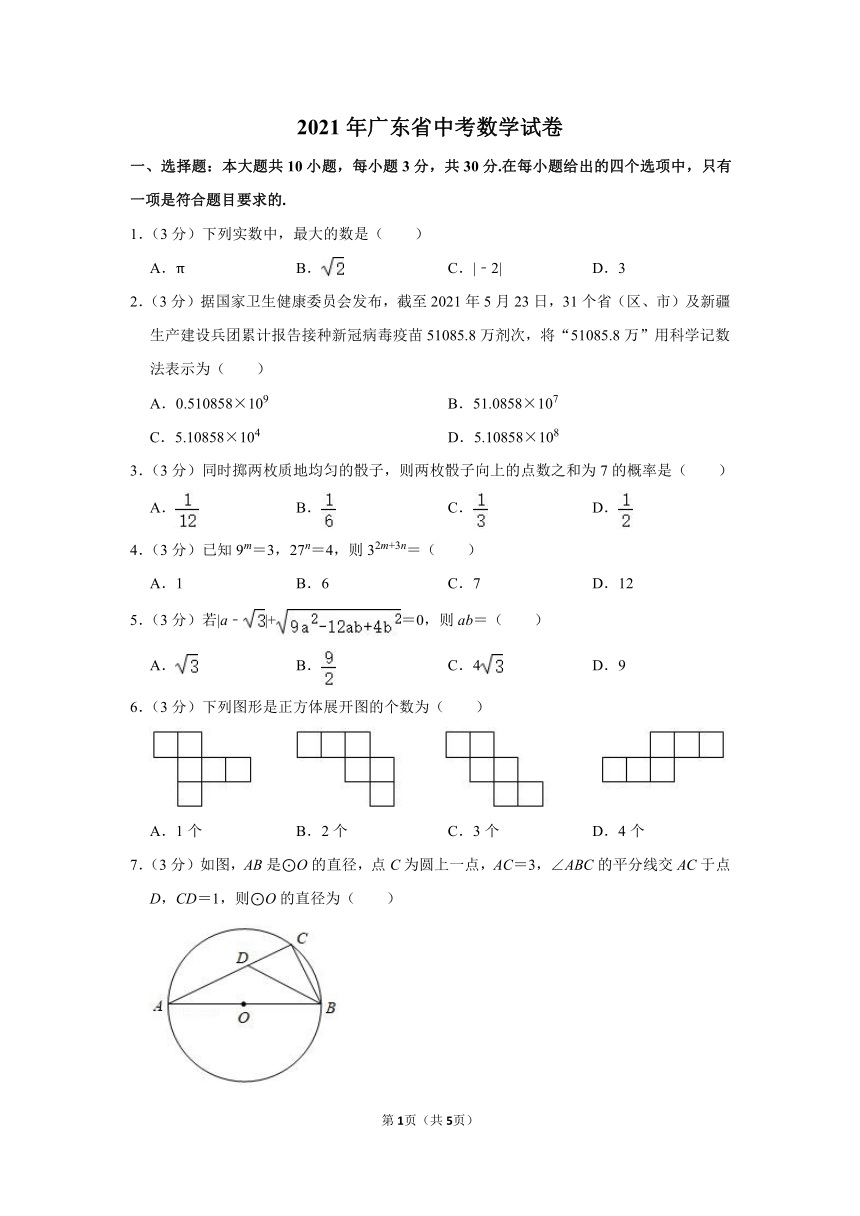
2021年广东省中考数学试卷
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(3分)下列实数中,最大的数是( )
A.π B. C.|﹣2| D.3
2.(3分)据国家卫生健康委员会发布,截至2021年5月23日,31个省(区、市)及新疆生产建设兵团累计报告接种新冠病毒疫苗51085.8万剂次,将“51085.8万”用科学记数法表示为( )
A.0.510858×109 B.51.0858×107
C.5.10858×104 D.5.10858×108
3.(3分)同时掷两枚质地均匀的骰子,则两枚骰子向上的点数之和为7的概率是( )
A. B. C. D.
4.(3分)已知9m=3,27n=4,则32m+3n=( )
A.1 B.6 C.7 D.12
5.(3分)若|a﹣|+=0,则ab=( )
A. B. C.4 D.9
6.(3分)下列图形是正方体展开图的个数为( )
A.1个 B.2个 C.3个 D.4个
7.(3分)如图,AB是⊙O的直径,点C为圆上一点,AC=3,∠ABC的平分线交AC于点D,CD=1,则⊙O的直径为( )
A. B.2 C.1 D.2
8.(3分)设6﹣的整数部分为a,小数部分为b,则(2a+)b的值是( )
A.6 B.2 C.12 D.9
9.(3分)我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,此公式与古希腊几何学家海伦提出的公式如出一辙,即三角形的三边长分别为a,b,c,记p=,则其面积S=.这个公式也被称为海伦﹣秦九韶公式.若p=5,c=4,则此三角形面积的最大值为( )
A. B.4 C.2 D.5
10.(3分)设O为坐标原点,点A、B为抛物线y=x2上的两个动点,且OA⊥OB.连接点A、B,过O作OC⊥AB于点C,则点C到y轴距离的最大值( )
A. B. C. D.1
二、填空题:本大题7小题,每小题4分,共28分.
11.(4分)二元一次方程组的解为 .
12.(4分)把抛物线y=2x2+1向左平移1个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为 .
13.(4分)如图,等腰直角三角形ABC中,∠A=90°,BC=4.分别以点B、点C为圆心,线段BC长的一半为半径作圆弧,交AB、BC、AC于点D、E、F,则图中阴影部分的面积为 .
14.(4分)若一元二次方程x2+bx+c=0(b,c为常数)的两根x1,x2满足﹣3<x1<﹣1,1<x2<3,则符合条件的一个方程为 .
15.(4分)若x+=且0<x<1,则x2﹣= .
16.(4分)如图,在 ABCD中,AD=5,AB=12,sinA=.过点D作DE⊥AB,垂足为E,则sin∠BCE= .
17.(4分)在△ABC中,∠ABC=90°,AB=2,BC=3.点D为平面上一个动点,∠ADB=45°,则线段CD长度的最小值为 .
三、解答题(一):本大题共3小题,每小题6分,共18分.
18.(6分)解不等式组.
19.(6分)某中学九年级举办中华优秀传统文化知识竞赛.用简单随机抽样的方法,从该年级全体600名学生中抽取20名,其竞赛成绩如图:
(1)求这20名学生成绩的众数,中位数和平均数;
(2)若规定成绩大于或等于90分为优秀等级,试估计该年级获优秀等级的学生人数.
20.(6分)如图,在Rt△ABC中,∠A=90°,作BC的垂直平分线交AC于点D,延长AC至点E,使CE=AB.
(1)若AE=1,求△ABD的周长;
(2)若AD=BD,求tan∠ABC的值.
四、解答题(二):本大题共3小题,每小题8分,共24分。
21.(8分)在平面直角坐标系xOy中,一次函数y=kx+b(k>0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=图象的一个交点为P(1,m).
(1)求m的值;
(2)若PA=2AB,求k的值.
22.(8分)端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元,某商家用8000元购进的猪肉粽和用6000元购进的豆沙粽盒数相同.在销售中,该商家发现猪肉粽每盒售价50元时,每天可售出100盒;每盒售价提高1元时,每天少售出2盒.
(1)求猪肉粽和豆沙粽每盒的进价;
(2)设猪肉粽每盒售价x元(50≤x≤65),y表示该商家每天销售猪肉粽的利润(单位:元),求y关于x的函数解析式并求最大利润.
23.(8分)如图,边长为1的正方形ABCD中,点E为AD的中点.连接BE,将△ABE沿BE折叠得到△FBE,BF交AC于点G,求CG的长.
五、解答题(三):本大题共2小题,每小题10分,共20分。
24.(10分)如图,在四边形ABCD中,AB∥CD,AB≠CD,∠ABC=90°,点E、F分别在线段BC、AD上,且EF∥CD,AB=AF,CD=DF.
(1)求证:CF⊥FB;
(2)求证:以AD为直径的圆与BC相切;
(3)若EF=2,∠DFE=120°,求△ADE的面积.
25.(10分)已知二次函数y=ax2+bx+c的图象过点(﹣1,0),且对任意实数x,都有4x﹣12≤ax2+bx+c≤2x2﹣8x+6.
(1)求该二次函数的解析式;
(2)若(1)中二次函数图象与x轴的正半轴交点为A,与y轴交点为C;点M是(1)中二次函数图象上的动点.问在x轴上是否存在点N,使得以A、C、M、N为顶点的四边形是平行四边形.若存在,求出所有满足条件的点N的坐标;若不存在,请说明理由.
第19页(共24页)
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(3分)下列实数中,最大的数是( )
A.π B. C.|﹣2| D.3
2.(3分)据国家卫生健康委员会发布,截至2021年5月23日,31个省(区、市)及新疆生产建设兵团累计报告接种新冠病毒疫苗51085.8万剂次,将“51085.8万”用科学记数法表示为( )
A.0.510858×109 B.51.0858×107
C.5.10858×104 D.5.10858×108
3.(3分)同时掷两枚质地均匀的骰子,则两枚骰子向上的点数之和为7的概率是( )
A. B. C. D.
4.(3分)已知9m=3,27n=4,则32m+3n=( )
A.1 B.6 C.7 D.12
5.(3分)若|a﹣|+=0,则ab=( )
A. B. C.4 D.9
6.(3分)下列图形是正方体展开图的个数为( )
A.1个 B.2个 C.3个 D.4个
7.(3分)如图,AB是⊙O的直径,点C为圆上一点,AC=3,∠ABC的平分线交AC于点D,CD=1,则⊙O的直径为( )
A. B.2 C.1 D.2
8.(3分)设6﹣的整数部分为a,小数部分为b,则(2a+)b的值是( )
A.6 B.2 C.12 D.9
9.(3分)我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,此公式与古希腊几何学家海伦提出的公式如出一辙,即三角形的三边长分别为a,b,c,记p=,则其面积S=.这个公式也被称为海伦﹣秦九韶公式.若p=5,c=4,则此三角形面积的最大值为( )
A. B.4 C.2 D.5
10.(3分)设O为坐标原点,点A、B为抛物线y=x2上的两个动点,且OA⊥OB.连接点A、B,过O作OC⊥AB于点C,则点C到y轴距离的最大值( )
A. B. C. D.1
二、填空题:本大题7小题,每小题4分,共28分.
11.(4分)二元一次方程组的解为 .
12.(4分)把抛物线y=2x2+1向左平移1个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为 .
13.(4分)如图,等腰直角三角形ABC中,∠A=90°,BC=4.分别以点B、点C为圆心,线段BC长的一半为半径作圆弧,交AB、BC、AC于点D、E、F,则图中阴影部分的面积为 .
14.(4分)若一元二次方程x2+bx+c=0(b,c为常数)的两根x1,x2满足﹣3<x1<﹣1,1<x2<3,则符合条件的一个方程为 .
15.(4分)若x+=且0<x<1,则x2﹣= .
16.(4分)如图,在 ABCD中,AD=5,AB=12,sinA=.过点D作DE⊥AB,垂足为E,则sin∠BCE= .
17.(4分)在△ABC中,∠ABC=90°,AB=2,BC=3.点D为平面上一个动点,∠ADB=45°,则线段CD长度的最小值为 .
三、解答题(一):本大题共3小题,每小题6分,共18分.
18.(6分)解不等式组.
19.(6分)某中学九年级举办中华优秀传统文化知识竞赛.用简单随机抽样的方法,从该年级全体600名学生中抽取20名,其竞赛成绩如图:
(1)求这20名学生成绩的众数,中位数和平均数;
(2)若规定成绩大于或等于90分为优秀等级,试估计该年级获优秀等级的学生人数.
20.(6分)如图,在Rt△ABC中,∠A=90°,作BC的垂直平分线交AC于点D,延长AC至点E,使CE=AB.
(1)若AE=1,求△ABD的周长;
(2)若AD=BD,求tan∠ABC的值.
四、解答题(二):本大题共3小题,每小题8分,共24分。
21.(8分)在平面直角坐标系xOy中,一次函数y=kx+b(k>0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=图象的一个交点为P(1,m).
(1)求m的值;
(2)若PA=2AB,求k的值.
22.(8分)端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元,某商家用8000元购进的猪肉粽和用6000元购进的豆沙粽盒数相同.在销售中,该商家发现猪肉粽每盒售价50元时,每天可售出100盒;每盒售价提高1元时,每天少售出2盒.
(1)求猪肉粽和豆沙粽每盒的进价;
(2)设猪肉粽每盒售价x元(50≤x≤65),y表示该商家每天销售猪肉粽的利润(单位:元),求y关于x的函数解析式并求最大利润.
23.(8分)如图,边长为1的正方形ABCD中,点E为AD的中点.连接BE,将△ABE沿BE折叠得到△FBE,BF交AC于点G,求CG的长.
五、解答题(三):本大题共2小题,每小题10分,共20分。
24.(10分)如图,在四边形ABCD中,AB∥CD,AB≠CD,∠ABC=90°,点E、F分别在线段BC、AD上,且EF∥CD,AB=AF,CD=DF.
(1)求证:CF⊥FB;
(2)求证:以AD为直径的圆与BC相切;
(3)若EF=2,∠DFE=120°,求△ADE的面积.
25.(10分)已知二次函数y=ax2+bx+c的图象过点(﹣1,0),且对任意实数x,都有4x﹣12≤ax2+bx+c≤2x2﹣8x+6.
(1)求该二次函数的解析式;
(2)若(1)中二次函数图象与x轴的正半轴交点为A,与y轴交点为C;点M是(1)中二次函数图象上的动点.问在x轴上是否存在点N,使得以A、C、M、N为顶点的四边形是平行四边形.若存在,求出所有满足条件的点N的坐标;若不存在,请说明理由.
第19页(共24页)
同课章节目录
