【核心考点集训】第二单元《因数和倍数》学案--人教版五年级下册
文档属性
| 名称 | 【核心考点集训】第二单元《因数和倍数》学案--人教版五年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 384.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-22 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
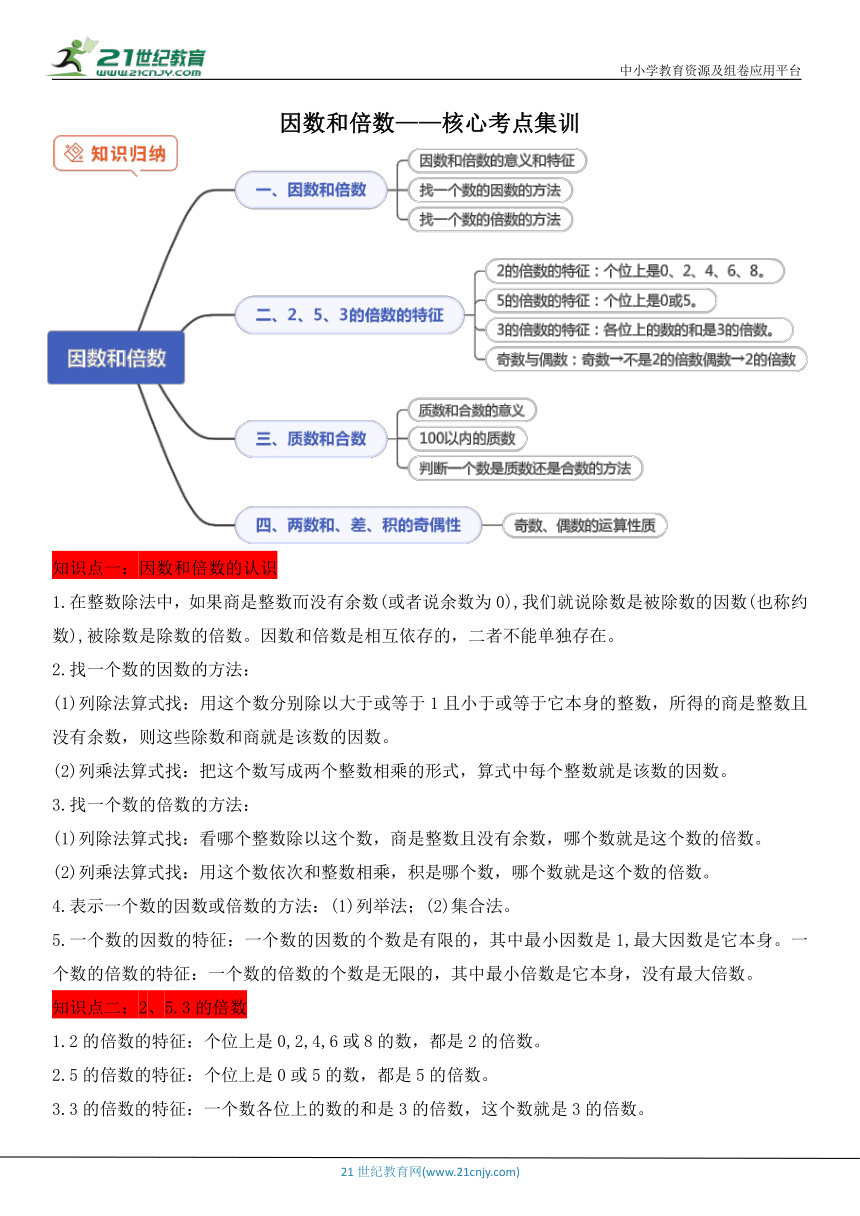
因数和倍数——核心考点集训
知识点一:因数和倍数的认识
1.在整数除法中,如果商是整数而没有余数(或者说余数为0),我们就说除数是被除数的因数(也称约数),被除数是除数的倍数。因数和倍数是相互依存的,二者不能单独存在。
2.找一个数的因数的方法:
(1)列除法算式找:用这个数分别除以大于或等于1且小于或等于它本身的整数,所得的商是整数且没有余数,则这些除数和商就是该数的因数。
(2)列乘法算式找:把这个数写成两个整数相乘的形式,算式中每个整数就是该数的因数。
3.找一个数的倍数的方法:
(1)列除法算式找:看哪个整数除以这个数,商是整数且没有余数,哪个数就是这个数的倍数。
(2)列乘法算式找:用这个数依次和整数相乘,积是哪个数,哪个数就是这个数的倍数。
4.表示一个数的因数或倍数的方法:(1)列举法;(2)集合法。
5.一个数的因数的特征:一个数的因数的个数是有限的,其中最小因数是1,最大因数是它本身。一个数的倍数的特征:一个数的倍数的个数是无限的,其中最小倍数是它本身,没有最大倍数。
知识点二:2、5.3的倍数
1.2的倍数的特征:个位上是0,2,4,6或8的数,都是2的倍数。
2.5的倍数的特征:个位上是0或5的数,都是5的倍数。
3.3的倍数的特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数。
4.整数中,是2的倍数的数叫作偶数(0也是偶数),不是2的倍数的数叫作奇数。最小的偶数是0,最小的奇数是1,没有最大的奇数和偶数。
知识点三:质数和合数
1.一个数,如果只有1和它本身两个因数,这样的数叫作质数(或素数);一个数,如果除了1和它本身还有别的因数,这样的数叫作合数。
2.质数只有两个因数,合数有两个以上的因数,因此1不是质数,也不是合数。判断一个数是质数还是合数,只要看这个数的因数的个数就可以了。
3.最小的质数是2,最小的合数是4。
4.100以内的质数:2,3,5,7,11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73,79,83, 89,97
知识点四:奇数、偶数的运算性质
1.两数之和的奇偶性:奇数+奇数=偶数;奇数+偶数=奇数;偶数+偶数=偶数。
2.两数之差的奇偶性:奇数-奇数=偶数,偶数-偶数=偶数,奇数-偶数=奇数,偶数-奇数=奇数。
3.两数之积的奇偶性:奇数×奇数=奇数,偶数×偶数=偶数,奇数×偶数=偶数。
【典例1】根据2、3、5的倍数的特征解决组数问题
5□□0是有两个相同数字的四位数,已知它同时是2、3和5的倍数。这个四位数最大是( ),最小是( )。
【典例2】设中间数解决与连续奇(偶)数有关的问题
三个连续偶数的和是72,其中最大的一个偶数是( )。
【典例3】用推理法解决较复杂的倍数问题
将自然数3、4、5依次重复写下去,得到一个多位数345345345…,一共2022位。这个数是3的倍数吗
【典例4】利用奇数、偶数的运算性质解决实际问题
爸爸给姐姐和弟弟买礼物共花了61元。如果给姐姐买礼物的钱数是奇数,则给弟弟买礼物的钱数是奇数还是偶数 说一说你的理由。
【典例5】根据数的奇偶性解决问题
有12个杯子全部杯口朝上,每次将其中的7个杯子同时翻转,最少经过( )次翻转,可以使杯口全部朝下。
【典例6】根据2、5和3的倍数特征解决实际问题
五(1)班全体同学报名参加志愿活动,老师把他们分成若干小组,如果每3人一组或5人一组都少2人。已知总人数大于40且小于50。五(1)班共有多少人
【典例7】运用质数、合数有关的知识解决问题
两个质数的和是小于100的奇数,并且是11的倍数,这两个质数可能是多少
1.□□20是有两个相同数字的四位数,已知它同时是2、3和5的倍数,这个四位数最大是( ),最小是( )。
2.三个连续偶数的和是144,其中最小的一个偶数是( )。
3.六位数3ABABA是6的倍数,这样的六位数共有多少个
4.一个长方形的面积是奇数,这个长方形的长是23 cm,这个长方形的宽可能是一个偶数吗 并说明理由。
5.有14个杯子全部杯口朝上,每次将其中的5个杯子同时翻转,最少经过( )次翻转,可以使杯口全部朝下。
一盒羽毛球,5个5个地取,最后剩下1个;3个3个地取,最后剩下1个;2个2个地取,最后还是剩下1个,这盒羽毛球最少有多少个
7.一个长方形的长和宽都是整厘米数,而且都是质数,周长是36 cm。这个长方形的面积最大是多少平方厘米
参考答案
【典例1】根据2、3、5的倍数的特征解决组数问题
5□□0是有两个相同数字的四位数,已知它同时是2、3和5的倍数。这个四位数最大是( 5880 ),最小是( 5010 )。
【典例2】设中间数解决与连续奇(偶)数有关的问题
三个连续偶数的和是72,其中最大的一个偶数是( 26 )。
【典例3】用推理法解决较复杂的倍数问题
将自然数3、4、5依次重复写下去,得到一个多位数345345345…,一共2022位。这个数是3的倍数吗
2022÷3=674(组)3+4+5=12
12是3的倍数,674个12也是3的倍数。答:这个数是3的倍数。
【典例4】利用奇数、偶数的运算性质解决实际问题
爸爸给姐姐和弟弟买礼物共花了61元。如果给姐姐买礼物的钱数是奇数,则给弟弟买礼物的钱数是奇数还是偶数 说一说你的理由。
给弟弟买礼物的钱数是偶数。
理由:因为61是奇数,给姐姐买礼物的钱数是奇数,奇数一奇数=偶数,所以给弟弟买礼物的钱数是偶数。
【典例5】根据数的奇偶性解决问题
有12个杯子全部杯口朝上,每次将其中的7个杯子同时翻转,最少经过( 4 )次翻转,可以使杯口全部朝下。
【典例6】根据2、5和3的倍数特征解决实际问题
五(1)班全体同学报名参加志愿活动,老师把他们分成若干小组,如果每3人一组或5人一组都少2人。已知总人数大于40且小于50。五(1)班共有多少人
因为3人一组或5人一组都少2人,所以总人数加2是3的倍数也是5的倍数。
40~50之间3的倍数有42、45、48,5的倍数只有45。
45-2=43(人)
答:五(1)班共有43人。
【典例7】运用质数、合数有关的知识解决问题
两个质数的和是小于100的奇数,并且是11的倍数,这两个质数可能是多少
11-2=9,9不是质数 33-2=31,31是质数 55-2=53,53是质数
77-2=75,75不是质数 99-2=97,97是质数
这两个质数可能是2和31,2和53,2和97。
1.□□20是有两个相同数字的四位数,已知它同时是2、3和5的倍数,这个四位数最大是( 8820 ),最小是( 1020 )。
2.三个连续偶数的和是144,其中最小的一个偶数是( 46 )。
3.六位数3ABABA是6的倍数,这样的六位数共有多少个
4×5=20(个)
4.一个长方形的面积是奇数,这个长方形的长是23 cm,这个长方形的宽可能是一个偶数吗 并说明理由。
不可能。面积是一个奇数,23是一个奇数,根据奇数×奇数=奇数,奇数×偶数=偶数,这个长方形的宽不可能是偶数。
5.有14个杯子全部杯口朝上,每次将其中的5个杯子同时翻转,最少经过( 4 )次翻转,可以使杯口全部朝下。
一盒羽毛球,5个5个地取,最后剩下1个;3个3个地取,最后剩下1个;2个2个地取,最后还是剩下1个,这盒羽毛球最少有多少个
羽毛球的个数减1同时是2、3、5的倍数。
假设羽毛球有□0+1个,口0是3的倍数,最小是30。
30+1=31(个)
答:这盒羽毛球最少有31个。
7.一个长方形的长和宽都是整厘米数,而且都是质数,周长是36 cm。这个长方形的面积最大是多少平方厘米
长和宽的和:36÷2=18(cm) 18=5+13=7+11
长方形的长和宽可能分别是13cm和5cm,11 cm和7cm。
面积分别是:13×5=65(cm ) 11×7=77(cm )
65<77
答:这个长方形的面积最大是77 cm 。
21世纪教育网(www.21cnjy.com)
因数和倍数——核心考点集训
知识点一:因数和倍数的认识
1.在整数除法中,如果商是整数而没有余数(或者说余数为0),我们就说除数是被除数的因数(也称约数),被除数是除数的倍数。因数和倍数是相互依存的,二者不能单独存在。
2.找一个数的因数的方法:
(1)列除法算式找:用这个数分别除以大于或等于1且小于或等于它本身的整数,所得的商是整数且没有余数,则这些除数和商就是该数的因数。
(2)列乘法算式找:把这个数写成两个整数相乘的形式,算式中每个整数就是该数的因数。
3.找一个数的倍数的方法:
(1)列除法算式找:看哪个整数除以这个数,商是整数且没有余数,哪个数就是这个数的倍数。
(2)列乘法算式找:用这个数依次和整数相乘,积是哪个数,哪个数就是这个数的倍数。
4.表示一个数的因数或倍数的方法:(1)列举法;(2)集合法。
5.一个数的因数的特征:一个数的因数的个数是有限的,其中最小因数是1,最大因数是它本身。一个数的倍数的特征:一个数的倍数的个数是无限的,其中最小倍数是它本身,没有最大倍数。
知识点二:2、5.3的倍数
1.2的倍数的特征:个位上是0,2,4,6或8的数,都是2的倍数。
2.5的倍数的特征:个位上是0或5的数,都是5的倍数。
3.3的倍数的特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数。
4.整数中,是2的倍数的数叫作偶数(0也是偶数),不是2的倍数的数叫作奇数。最小的偶数是0,最小的奇数是1,没有最大的奇数和偶数。
知识点三:质数和合数
1.一个数,如果只有1和它本身两个因数,这样的数叫作质数(或素数);一个数,如果除了1和它本身还有别的因数,这样的数叫作合数。
2.质数只有两个因数,合数有两个以上的因数,因此1不是质数,也不是合数。判断一个数是质数还是合数,只要看这个数的因数的个数就可以了。
3.最小的质数是2,最小的合数是4。
4.100以内的质数:2,3,5,7,11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73,79,83, 89,97
知识点四:奇数、偶数的运算性质
1.两数之和的奇偶性:奇数+奇数=偶数;奇数+偶数=奇数;偶数+偶数=偶数。
2.两数之差的奇偶性:奇数-奇数=偶数,偶数-偶数=偶数,奇数-偶数=奇数,偶数-奇数=奇数。
3.两数之积的奇偶性:奇数×奇数=奇数,偶数×偶数=偶数,奇数×偶数=偶数。
【典例1】根据2、3、5的倍数的特征解决组数问题
5□□0是有两个相同数字的四位数,已知它同时是2、3和5的倍数。这个四位数最大是( ),最小是( )。
【典例2】设中间数解决与连续奇(偶)数有关的问题
三个连续偶数的和是72,其中最大的一个偶数是( )。
【典例3】用推理法解决较复杂的倍数问题
将自然数3、4、5依次重复写下去,得到一个多位数345345345…,一共2022位。这个数是3的倍数吗
【典例4】利用奇数、偶数的运算性质解决实际问题
爸爸给姐姐和弟弟买礼物共花了61元。如果给姐姐买礼物的钱数是奇数,则给弟弟买礼物的钱数是奇数还是偶数 说一说你的理由。
【典例5】根据数的奇偶性解决问题
有12个杯子全部杯口朝上,每次将其中的7个杯子同时翻转,最少经过( )次翻转,可以使杯口全部朝下。
【典例6】根据2、5和3的倍数特征解决实际问题
五(1)班全体同学报名参加志愿活动,老师把他们分成若干小组,如果每3人一组或5人一组都少2人。已知总人数大于40且小于50。五(1)班共有多少人
【典例7】运用质数、合数有关的知识解决问题
两个质数的和是小于100的奇数,并且是11的倍数,这两个质数可能是多少
1.□□20是有两个相同数字的四位数,已知它同时是2、3和5的倍数,这个四位数最大是( ),最小是( )。
2.三个连续偶数的和是144,其中最小的一个偶数是( )。
3.六位数3ABABA是6的倍数,这样的六位数共有多少个
4.一个长方形的面积是奇数,这个长方形的长是23 cm,这个长方形的宽可能是一个偶数吗 并说明理由。
5.有14个杯子全部杯口朝上,每次将其中的5个杯子同时翻转,最少经过( )次翻转,可以使杯口全部朝下。
一盒羽毛球,5个5个地取,最后剩下1个;3个3个地取,最后剩下1个;2个2个地取,最后还是剩下1个,这盒羽毛球最少有多少个
7.一个长方形的长和宽都是整厘米数,而且都是质数,周长是36 cm。这个长方形的面积最大是多少平方厘米
参考答案
【典例1】根据2、3、5的倍数的特征解决组数问题
5□□0是有两个相同数字的四位数,已知它同时是2、3和5的倍数。这个四位数最大是( 5880 ),最小是( 5010 )。
【典例2】设中间数解决与连续奇(偶)数有关的问题
三个连续偶数的和是72,其中最大的一个偶数是( 26 )。
【典例3】用推理法解决较复杂的倍数问题
将自然数3、4、5依次重复写下去,得到一个多位数345345345…,一共2022位。这个数是3的倍数吗
2022÷3=674(组)3+4+5=12
12是3的倍数,674个12也是3的倍数。答:这个数是3的倍数。
【典例4】利用奇数、偶数的运算性质解决实际问题
爸爸给姐姐和弟弟买礼物共花了61元。如果给姐姐买礼物的钱数是奇数,则给弟弟买礼物的钱数是奇数还是偶数 说一说你的理由。
给弟弟买礼物的钱数是偶数。
理由:因为61是奇数,给姐姐买礼物的钱数是奇数,奇数一奇数=偶数,所以给弟弟买礼物的钱数是偶数。
【典例5】根据数的奇偶性解决问题
有12个杯子全部杯口朝上,每次将其中的7个杯子同时翻转,最少经过( 4 )次翻转,可以使杯口全部朝下。
【典例6】根据2、5和3的倍数特征解决实际问题
五(1)班全体同学报名参加志愿活动,老师把他们分成若干小组,如果每3人一组或5人一组都少2人。已知总人数大于40且小于50。五(1)班共有多少人
因为3人一组或5人一组都少2人,所以总人数加2是3的倍数也是5的倍数。
40~50之间3的倍数有42、45、48,5的倍数只有45。
45-2=43(人)
答:五(1)班共有43人。
【典例7】运用质数、合数有关的知识解决问题
两个质数的和是小于100的奇数,并且是11的倍数,这两个质数可能是多少
11-2=9,9不是质数 33-2=31,31是质数 55-2=53,53是质数
77-2=75,75不是质数 99-2=97,97是质数
这两个质数可能是2和31,2和53,2和97。
1.□□20是有两个相同数字的四位数,已知它同时是2、3和5的倍数,这个四位数最大是( 8820 ),最小是( 1020 )。
2.三个连续偶数的和是144,其中最小的一个偶数是( 46 )。
3.六位数3ABABA是6的倍数,这样的六位数共有多少个
4×5=20(个)
4.一个长方形的面积是奇数,这个长方形的长是23 cm,这个长方形的宽可能是一个偶数吗 并说明理由。
不可能。面积是一个奇数,23是一个奇数,根据奇数×奇数=奇数,奇数×偶数=偶数,这个长方形的宽不可能是偶数。
5.有14个杯子全部杯口朝上,每次将其中的5个杯子同时翻转,最少经过( 4 )次翻转,可以使杯口全部朝下。
一盒羽毛球,5个5个地取,最后剩下1个;3个3个地取,最后剩下1个;2个2个地取,最后还是剩下1个,这盒羽毛球最少有多少个
羽毛球的个数减1同时是2、3、5的倍数。
假设羽毛球有□0+1个,口0是3的倍数,最小是30。
30+1=31(个)
答:这盒羽毛球最少有31个。
7.一个长方形的长和宽都是整厘米数,而且都是质数,周长是36 cm。这个长方形的面积最大是多少平方厘米
长和宽的和:36÷2=18(cm) 18=5+13=7+11
长方形的长和宽可能分别是13cm和5cm,11 cm和7cm。
面积分别是:13×5=65(cm ) 11×7=77(cm )
65<77
答:这个长方形的面积最大是77 cm 。
21世纪教育网(www.21cnjy.com)
