第1-3章复习卷(含解析)-2024-2025学年数学九年级下册北师大版
文档属性
| 名称 | 第1-3章复习卷(含解析)-2024-2025学年数学九年级下册北师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-23 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第1-3章复习卷-2024-2025学年数学九年级下册北师大版
一、单选题
1.如果圆锥侧面展开图的面积是,母线长是5,则这个圆锥的底面半径是( )
A.3 B.4 C.5 D.6
2.函数的顶点坐标是( )
A. B. C. D.
3.如图,在中,,若,,则( )
A. B. C. D.
4.如图,四边形内接于,若,则的度数是( )
A. B. C. D.
5.已知是斜边的中线,若,则( )
A. B. C. D.
6.二次函数(为常数,)部分,的对应值如表:
… 0 1 3 4 …
… 1 1 5 …
则下列判断中正确的是( )
A.函数图象的开口向下 B.当时,随的增大而增大
C.当时, D.最小值为
7.如图,在中,弦,半径于点,,则的半径为( )
A. B. C. D.5
8.如图,在边长为的正方形中,对角线与交于点,分别以,,,为圆心,,,,长为半径画弧,则图中阴影部分的面积为( )
A. B. C. D.
二、填空题
9.将抛物线向左平移2个单位,得到的抛物线解析式为 .
10.已知两个不同的点,都在二次函数.的图象上,则代数式的值为 .
11.如图,、、是⊙的切线,切点分别是P、C、D.若,,则的长是 .
12.如图,在中,,,.点是内部一点,且,连接,则长的最小值为 .
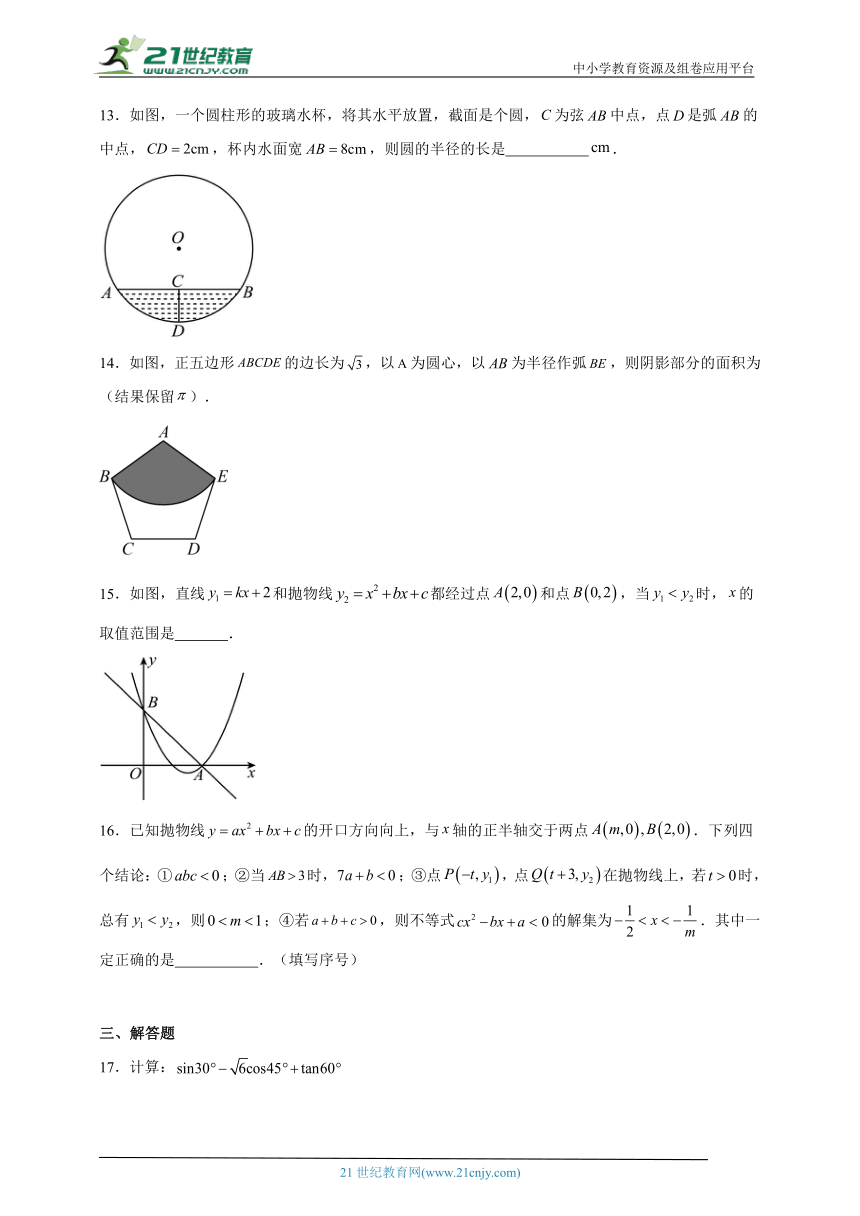
13.如图,一个圆柱形的玻璃水杯,将其水平放置,截面是个圆,为弦中点,点是弧的中点,,杯内水面宽,则圆的半径的长是 .
14.如图,正五边形的边长为,以为圆心,以为半径作弧,则阴影部分的面积为 (结果保留).
15.如图,直线和抛物线都经过点和点,当时,的取值范围是 .
16.已知抛物线的开口方向向上,与轴的正半轴交于两点.下列四个结论:①;②当时,;③点,点在抛物线上,若时,总有,则;④若,则不等式的解集为.其中一定正确的是 .(填写序号)
三、解答题
17.计算:
18.在二次函数中.
(1)若该函数图象的顶点在x轴上,求t的值;
(2)若点在该函数图象上,令,求证:.
19.如图,是的直径,四边形是矩形,与圆相交于点E,,D是上的点,,与交于点C,的半径为.
(1)求的长.
(2)若,求的长.
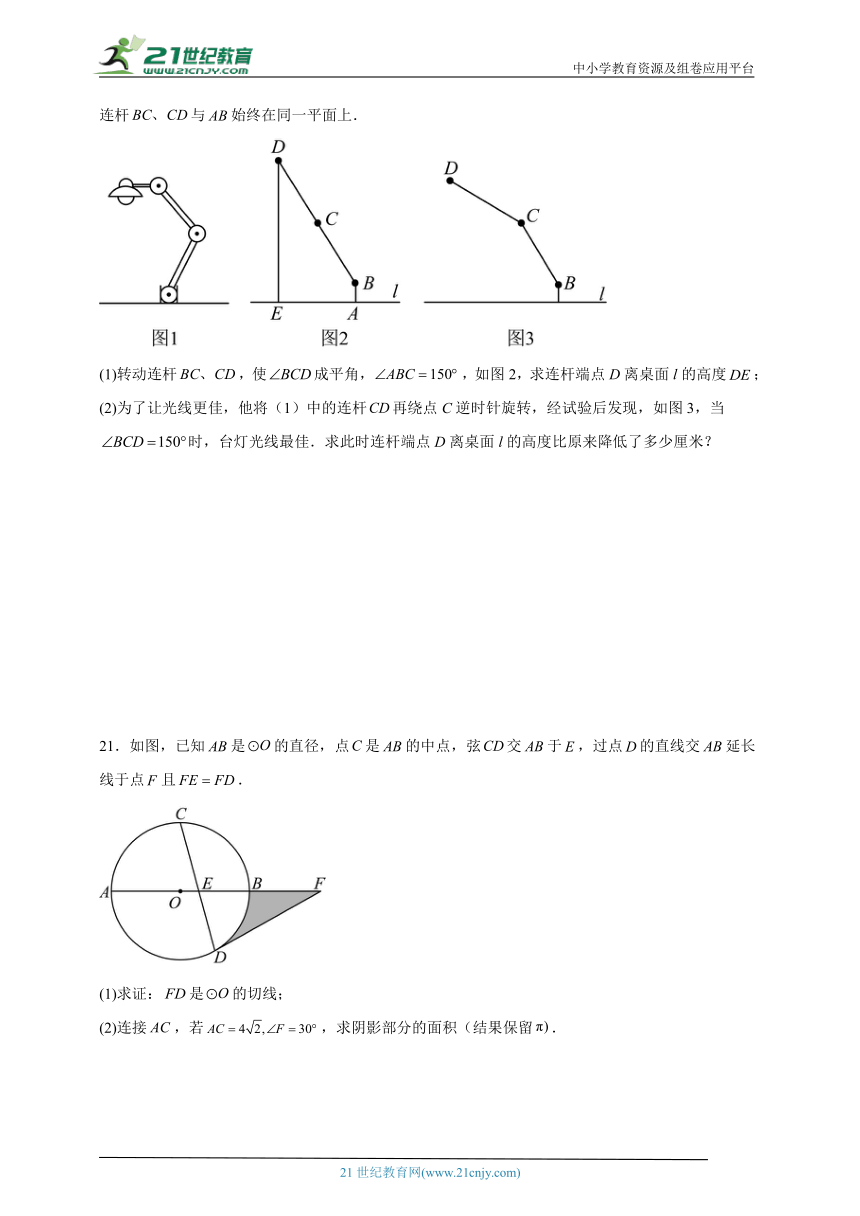
20.小颖爸爸买了一盏新台灯,如图1放置在水平桌面l上,底座的高为,长度均为的连杆与始终在同一平面上.
(1)转动连杆,使成平角,,如图2,求连杆端点D离桌面l的高度;
(2)为了让光线更佳,他将(1)中的连杆再绕点C逆时针旋转,经试验后发现,如图3,当时,台灯光线最佳.求此时连杆端点D离桌面l的高度比原来降低了多少厘米?
21.如图,已知是的直径,点是的中点,弦交于,过点的直线交延长线于点且.
(1)求证:是的切线;
(2)连接,若,求阴影部分的面积(结果保留.
22.如图,中,,点I是的内心.
(1)O是边上一点,以r为半径的恰好经过B、I两点,求r的值;
(2)过点I的直线l分别交边、边于点M、N.以下两个结论:①为定值;②为定值,其中只有一个结论是正确的,判断哪个结论正确并求出该定值.
23.综合与实践
【主题】优化洒水车为公路两侧绿化带浇水效率
【问题背景】如图1,洒水车沿着平行于公路绿化带方向行驶,同时向右侧绿化带浇水.数学兴趣小组的同学想了解洒水车要如何控制行驶路线与绿化带之间的距离,才能保证喷出的水能浇灌到整个绿化带,为解决这个问题,数学兴趣小组同学通过建立数学模型进行探索.
【数学建模】如图2,建立平面直角坐标系,可以把洒水车喷出水的内、外边缘抽象为平面直角坐标系中两条抛物线的部分图象;喷水口H离地竖直高度为,把绿化带横截面抽象为矩形,其水平宽度,竖直高度,表示洒水车和绿化带之间的距离.内边缘抛物线是由外边缘抛物线向左平移得到,外边缘抛物线最高点A离喷水口的水平距离为,高出喷水口.
【解决问题】
(1)求外边缘抛物线的函数分析式,并求喷出水的最大射程;
(2)请求出内边缘抛物线与x轴的正半轴交点B的坐标;
(3)要使洒水车行驶时喷出的水能浇灌到整个绿化带,请直接写出的取值范围.
《第1-3章复习卷-2024-2025学年数学九年级下册北师大版》参考答案
题号 1 2 3 4 5 6 7 8
答案 B B B C A B D C
1.B
【分析】本题主要考查了圆锥的计算,熟知圆锥的侧面积公式是解题的关键.根据圆锥的侧面积公式进行计算即可.
【详解】解:由题知,
令圆锥的底面半径为r,
则,
解得,
所以圆锥的底面半径为
故选:
2.B
【分析】本题考查二次函数的性质,解答本题的关键是根据顶点式写出顶点坐标.根据二次函数的解析式,可以直接写出该函数图象的顶点坐标.
【详解】解:二次函数,
该函数图象的顶点坐标为,
故选:B
3.B
【分析】本题考查了锐角三角函数的定义和勾股定理.设,可得,根据,得,根据勾股定理得,再根据正弦的定义计算即可.
【详解】解:设,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
故选:B.
4.C
【分析】本题考查院内接四边形的性质和圆周角定理.先根据圆周角定理得到,然后根据圆内接四边形的性质和邻补角的定义得到解题即可.
【详解】解:∵,
∴,
又∵四边形内接于,
∴,
又∵,
∴,
故选:C.
5.A
【分析】本题考查了直角三角形斜边中线的性质,解直角三角形.根据直角三角形斜边中线的性质,求得,推出,由,求得,据此求解即可.
【详解】解:∵是斜边的中线,
∴,
∴,
∵,
∴,
设,则,
∴,
∴,
故选:A.
6.B
【分析】本题考查了二次函数的性质,根据二次函数的性质并结合表格的数据逐项分析即可得解,熟练掌握二次函数的性质是解此题的关键.
【详解】解:由表格可得,该二次函数图象的对称轴为直线,当时,随着的增大而减小,当时,随着的增大而增大,故函数图象的开口向上,A错误;
当时,随的增大而增大,B正确;
当时,或,C错误;
当时,取得最小值,这个最小值小于,D错误;
故选:B.
7.D
【分析】本题考查了垂径定理、勾股定理,由垂径定理可得,再由勾股定理计算即可得解.
【详解】解:∵在中,弦,半径于点,
∴,
∴,
故选:D.
8.C
【分析】本题考查了正方形的性质,勾股定理,扇形面积公式,掌握知识点的应用是解题的关键.
由正方形的性质可得,,,,则,,故,先求出在中空白部分面积为,则在中阴影部分面积为图中阴影部分的面积.
【详解】解:如图,
∵四边形是正方形,
∴,,,,
∴,,
∴,
在中空白部分面积为:,
则在中阴影部分面积为:
,
∴图中阴影部分的面积为,
故选:.
9.
【分析】本题考查了二次函数图象的平移,熟练掌握二次函数图象的平移规律“左加右减,上加下减”是解答关键.
根据二次函数图象的平移规律“左加右减,上加下减”来进行求解.
【详解】解:将抛物线向左平移2个单位,
得到的抛物线解析式为.
故答案为:.
10.
【分析】本题主要考查二次函数的性质,根与系数的关系,熟练掌握二次函数的性质是解题的关键.根据题意得到,,由二次函数得到,即可得到答案.
【详解】解:点,都在二次函数.的图象上,
是方程,
,
点,纵坐标相等,
,
即,
点,都在二次函数.的图象上,
,
即,
.
故答案为:.
11.
【分析】由于、、是的切线,则,,求出的长即可求出的长.本题考查了切线长定理,两次运用切线长定理并利用等式的性质是解题的关键.
【详解】解:、为的切线,
,
、为的切线,
,
.
故答案为:4.
12./
【分析】本题主要考查圆的性质,平行四边形的性质,勾股定理,熟练掌握点的运动轨迹是解题的关键.设的中点为,连接,易知当点在上时,的值最小,过点作,交的延长线于点,根据勾股定理求出,即可得到答案.
【详解】解:,
,
,
,
,
点的轨迹是以为直径的圆的一部分.
设的中点为,连接,易知当点在上时,的值最小,过点作,交的延长线于点,
则,
,
,
,
,
.
故答案为:.
13.5
【分析】本题考查垂径定理,勾股定理.设圆的半径为,利用垂径定理和勾股定理,列出方程进行求解即可.
【详解】解:连接并延长,交圆于点,,,
∵,C为弦中点,
∴,,
∴平分,
∵为的中点,
∴点,重合,
∴,,三点共线,
设圆的半径为,则:,
由勾股定理,得:,
∴,
解得:;
故答案为:5.
14./
【分析】本题考查了扇形面积和正多边形内角和的计算.根据正多边形内角和公式求出正五边形的内角和,再求出的度数,利用扇形面积公式计算即可.
【详解】解:正五边形的内角和,
,
,
故答案为:.
15.或
【分析】本题考查了根据直线和抛物线交点确定不等式的解集.解题的关键在于对知识的熟练掌握与数形结合.
由题意知,当时,则的取值范围是抛物线图象在直线图象上方对应的所有的的取值,然后数形结合求解即可.
【详解】解:由题意知,当时,则的取值范围是抛物线图象在直线图象上方对应的所有的的取值,
∵图象交于点,点,
∴当时,或,
故答案为:或.
16.①②③
【分析】本题考查了二次函数的图象性质,抛物线与与轴的交点问题,根据抛物线的开口方向向上,与轴的正半轴交于两点,得,对称轴,,即可判断①是正确的;结合,得,此时对称轴为直线,整理得,即可判断②是正确的;再因为点,点在抛物线上,且,得,即,即可判断③是正确的;先得,得,结合,整理得,函数的开口向上,则,令解得,然后再进行分类讨论,即可作答.
【详解】解:∵抛物线的开口方向向上,与轴的正半轴交于两点.
∴,对称轴,
即,
在时,随的增大而减小,且,
把代入,得,
即
∴,
故①是正确的;
∵抛物线的开口方向向上,与轴的正半轴交于两点.
且,
∴,
∴对称轴为直线,
即,
∴,
故②是正确的;
∵点,点在抛物线上,且
∴,,
∵,且对称轴为直线,且抛物线的开口方向向上,
∴
∴;
∵抛物线与轴的正半轴交于两点.
∴,
故③是正确的;
∵抛物线与轴的正半轴交于两点.
∴,
∴,
∵对称轴为直线
∴,
∵,
∴
设函数,
∵,
∴开口向上,
则
令则,
解得,
∵函数的开口向上,
则不等式的解集为.
∵,
∴,
∴,
∵,
∴,
∴.
当时,则不等式的解集为.
当时,则,故不等式的解集为.
故④是不正确的;
故答案为:①②③.
17..
【分析】本题考查了实数的运算,特殊角的三角函数值,熟练掌握运算法则是解题的关键.
先把特殊角的三角函数值代入,再计算即可.
【详解】解:
18.(1);
(2)见解析.
【分析】本题考查了二次函数的性质,二次函数的最值,二次函数图象上点的坐标的特征,解题的关键是掌握二次函数的性质.
(1)根据顶点在轴上,顶点的纵坐标是0,求出即可;
(2)把点代入解析式得到,由得到,根据二次函数的性质即可证得结论.
【详解】(1)解:根据题意得:,
解得或,
,
的值为;
(2)证明:点在抛物线上,
,
,
,
,
有最大值,
.
19.(1)
(2)
【分析】本题考查了直角三角形的性质,弧长的计算,矩形的性质,是基础知识要熟练掌握.
(1)连接,过作于,在 中,由勾股定理得出的长,进而求得的长.
(2)连接,则在直角三角形中,可求得,过点作于,在直角三角形中,可求得,则得出的长度.
【详解】(1)解:连接,过作于,
则四边形是矩形,
∴,
在中,,
∴.
(2)解:连接,
在直角三角形中,∵,
,
∴,
过点作于,在直角三角形中,
,
,
,
.
20.(1)
(2)
【分析】此题考查的是解直角三角形的应用,掌握构造直角三角形的方法和用锐角三角函数解直角三角形是解决此题的关键.
(1)作于O,根据矩形的判定,可得四边形是矩形,先求出,然后根据锐角三角函数即可求出,从而求出;
(2)过C作于点G,于点K,根据锐角三角函数,即可求出,从而求出,再求出,利用锐角三角函数即可求出,从而求出此时连杆端点D离桌面l的高度,即可求出结论.
【详解】(1)解:如图2中,作于O.
∵,
∴四边形是矩形,
∴,
,
∵成平角,
∴,
∴,
∴;
(2)解:过点C作于点G,于点K,
由题意得,,
∴在中, ,
∴,
∴,
∵,
∴,
在中,,
∴,
∴此时连杆端点D离桌面l的高度为,
∴比原来降低了.
21.(1)见解析;
(2).
【分析】(1)根据切线的判断方法,利用等腰三角形的性质,圆周角定理得出即可;
(2)根据扇形面积,三角形面积的计算方法进行计算即可.
【详解】(1)证明:连接、,
是的中点,
,
,
,
,
,
,
,
,
,
,
是的切线;
(2)解:中,,
,
在中,,,,
,
,
,
.
【点睛】本题考查扇形面积的计算,切线的判定与性质,等腰三角形的性质,解直角三角形,掌握切线的判定方法以及扇形面积的计算方法是正确解答的关键.
22.(1)r的值为
(2)②正确,定值为
【分析】(1)连接并延长,交于点,连接,等边对等角得到,内心得到是的角平分线,推出,三线合一推出,证明,得到,设,则:,进行求解即可;
(2)连接并延长,交于点,作,连接,三线合一结合勾股定理求出的长,等积法求出的长,进而求出的值,等积法求出为定值,三角函数求出,进行判断即可.
【详解】(1)解:连接并延长,交于点,连接,则:,
∴,
∵点I是的内心,
∴是的角平分线,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
设,则:,
∴,
解得:;
(2)②正确,理由如下:
连接并延长,交于点,作,连接,
∵点I是的内心,
∴点I是的三条角平分线的交点,
∵,
∴,,
∴,
∵,
∴,
∵,
∴,即:,
∴,
在中,,
∴在中,,
∵,
∴,
即:,
∴;
故为定值;
在中,,
在中,,
∴,,
∴,
∵,随着的变化而变化,不是定值,
∴不是定值.
【点睛】本题考查与三角形的内心有关的计算,相似三角形的判定和性质,解直角三角形,等腰三角形的性质,等积法求线段的长等知识点,熟练掌握内心是三角形的三条角平分线的交点,添加辅助线构造特殊图形,是解题的关键.
23.(1),喷出水的最大射程为
(2)点B的坐标为
(3)
【分析】易得的顶点A的坐标,用顶点式表示出的分析式,进而把点H的坐标代入可得a的值,取,可得的长度;
设出平移后的分析式,进而把点H的坐标代入可得m的值,取,求得相应的x的值可得抛物线与x轴的正半轴交点B的坐标;
要使洒水车行驶时喷出的水能浇灌到整个绿化带,点D与点B重合或点F在上,分别求得对应的的长,可得的取值范围.
本题考查二次函数的应用.用待定系数法求得的分析式是解决本题的关键;易错点是根据二次函数的平移规律得到的分析式;难点是判断出洒水车行驶时喷出的水能浇灌到整个绿化带时,点D或点F对应的位置.
【详解】(1)解:由题意得:点是外边缘抛物线的顶点,
设,
抛物线过点,
,
,
外边缘抛物线的函数分析式为:,
当时,,
解得:,舍去,
喷出水的最大射程为.
(2)解:由左右平移得到,
设,
经过点,
,
解得:,舍去,
,
把代入,得:
解得:,舍去,
点B的坐标为.
(3)解:要使洒水车行驶时喷出的水能浇灌到整个绿化带,
点D与点B重合或点F在上,
当点D与点B重合时,,
当点F在上时,,
解得:,不合题意,舍去,
,
,
的取值范围是
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1-3章复习卷-2024-2025学年数学九年级下册北师大版
一、单选题
1.如果圆锥侧面展开图的面积是,母线长是5,则这个圆锥的底面半径是( )
A.3 B.4 C.5 D.6
2.函数的顶点坐标是( )
A. B. C. D.
3.如图,在中,,若,,则( )
A. B. C. D.
4.如图,四边形内接于,若,则的度数是( )
A. B. C. D.
5.已知是斜边的中线,若,则( )
A. B. C. D.
6.二次函数(为常数,)部分,的对应值如表:
… 0 1 3 4 …
… 1 1 5 …
则下列判断中正确的是( )
A.函数图象的开口向下 B.当时,随的增大而增大
C.当时, D.最小值为
7.如图,在中,弦,半径于点,,则的半径为( )
A. B. C. D.5
8.如图,在边长为的正方形中,对角线与交于点,分别以,,,为圆心,,,,长为半径画弧,则图中阴影部分的面积为( )
A. B. C. D.
二、填空题
9.将抛物线向左平移2个单位,得到的抛物线解析式为 .
10.已知两个不同的点,都在二次函数.的图象上,则代数式的值为 .
11.如图,、、是⊙的切线,切点分别是P、C、D.若,,则的长是 .
12.如图,在中,,,.点是内部一点,且,连接,则长的最小值为 .
13.如图,一个圆柱形的玻璃水杯,将其水平放置,截面是个圆,为弦中点,点是弧的中点,,杯内水面宽,则圆的半径的长是 .
14.如图,正五边形的边长为,以为圆心,以为半径作弧,则阴影部分的面积为 (结果保留).
15.如图,直线和抛物线都经过点和点,当时,的取值范围是 .
16.已知抛物线的开口方向向上,与轴的正半轴交于两点.下列四个结论:①;②当时,;③点,点在抛物线上,若时,总有,则;④若,则不等式的解集为.其中一定正确的是 .(填写序号)
三、解答题
17.计算:
18.在二次函数中.
(1)若该函数图象的顶点在x轴上,求t的值;
(2)若点在该函数图象上,令,求证:.
19.如图,是的直径,四边形是矩形,与圆相交于点E,,D是上的点,,与交于点C,的半径为.
(1)求的长.
(2)若,求的长.
20.小颖爸爸买了一盏新台灯,如图1放置在水平桌面l上,底座的高为,长度均为的连杆与始终在同一平面上.
(1)转动连杆,使成平角,,如图2,求连杆端点D离桌面l的高度;
(2)为了让光线更佳,他将(1)中的连杆再绕点C逆时针旋转,经试验后发现,如图3,当时,台灯光线最佳.求此时连杆端点D离桌面l的高度比原来降低了多少厘米?
21.如图,已知是的直径,点是的中点,弦交于,过点的直线交延长线于点且.
(1)求证:是的切线;
(2)连接,若,求阴影部分的面积(结果保留.
22.如图,中,,点I是的内心.
(1)O是边上一点,以r为半径的恰好经过B、I两点,求r的值;
(2)过点I的直线l分别交边、边于点M、N.以下两个结论:①为定值;②为定值,其中只有一个结论是正确的,判断哪个结论正确并求出该定值.
23.综合与实践
【主题】优化洒水车为公路两侧绿化带浇水效率
【问题背景】如图1,洒水车沿着平行于公路绿化带方向行驶,同时向右侧绿化带浇水.数学兴趣小组的同学想了解洒水车要如何控制行驶路线与绿化带之间的距离,才能保证喷出的水能浇灌到整个绿化带,为解决这个问题,数学兴趣小组同学通过建立数学模型进行探索.
【数学建模】如图2,建立平面直角坐标系,可以把洒水车喷出水的内、外边缘抽象为平面直角坐标系中两条抛物线的部分图象;喷水口H离地竖直高度为,把绿化带横截面抽象为矩形,其水平宽度,竖直高度,表示洒水车和绿化带之间的距离.内边缘抛物线是由外边缘抛物线向左平移得到,外边缘抛物线最高点A离喷水口的水平距离为,高出喷水口.
【解决问题】
(1)求外边缘抛物线的函数分析式,并求喷出水的最大射程;
(2)请求出内边缘抛物线与x轴的正半轴交点B的坐标;
(3)要使洒水车行驶时喷出的水能浇灌到整个绿化带,请直接写出的取值范围.
《第1-3章复习卷-2024-2025学年数学九年级下册北师大版》参考答案
题号 1 2 3 4 5 6 7 8
答案 B B B C A B D C
1.B
【分析】本题主要考查了圆锥的计算,熟知圆锥的侧面积公式是解题的关键.根据圆锥的侧面积公式进行计算即可.
【详解】解:由题知,
令圆锥的底面半径为r,
则,
解得,
所以圆锥的底面半径为
故选:
2.B
【分析】本题考查二次函数的性质,解答本题的关键是根据顶点式写出顶点坐标.根据二次函数的解析式,可以直接写出该函数图象的顶点坐标.
【详解】解:二次函数,
该函数图象的顶点坐标为,
故选:B
3.B
【分析】本题考查了锐角三角函数的定义和勾股定理.设,可得,根据,得,根据勾股定理得,再根据正弦的定义计算即可.
【详解】解:设,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
故选:B.
4.C
【分析】本题考查院内接四边形的性质和圆周角定理.先根据圆周角定理得到,然后根据圆内接四边形的性质和邻补角的定义得到解题即可.
【详解】解:∵,
∴,
又∵四边形内接于,
∴,
又∵,
∴,
故选:C.
5.A
【分析】本题考查了直角三角形斜边中线的性质,解直角三角形.根据直角三角形斜边中线的性质,求得,推出,由,求得,据此求解即可.
【详解】解:∵是斜边的中线,
∴,
∴,
∵,
∴,
设,则,
∴,
∴,
故选:A.
6.B
【分析】本题考查了二次函数的性质,根据二次函数的性质并结合表格的数据逐项分析即可得解,熟练掌握二次函数的性质是解此题的关键.
【详解】解:由表格可得,该二次函数图象的对称轴为直线,当时,随着的增大而减小,当时,随着的增大而增大,故函数图象的开口向上,A错误;
当时,随的增大而增大,B正确;
当时,或,C错误;
当时,取得最小值,这个最小值小于,D错误;
故选:B.
7.D
【分析】本题考查了垂径定理、勾股定理,由垂径定理可得,再由勾股定理计算即可得解.
【详解】解:∵在中,弦,半径于点,
∴,
∴,
故选:D.
8.C
【分析】本题考查了正方形的性质,勾股定理,扇形面积公式,掌握知识点的应用是解题的关键.
由正方形的性质可得,,,,则,,故,先求出在中空白部分面积为,则在中阴影部分面积为图中阴影部分的面积.
【详解】解:如图,
∵四边形是正方形,
∴,,,,
∴,,
∴,
在中空白部分面积为:,
则在中阴影部分面积为:
,
∴图中阴影部分的面积为,
故选:.
9.
【分析】本题考查了二次函数图象的平移,熟练掌握二次函数图象的平移规律“左加右减,上加下减”是解答关键.
根据二次函数图象的平移规律“左加右减,上加下减”来进行求解.
【详解】解:将抛物线向左平移2个单位,
得到的抛物线解析式为.
故答案为:.
10.
【分析】本题主要考查二次函数的性质,根与系数的关系,熟练掌握二次函数的性质是解题的关键.根据题意得到,,由二次函数得到,即可得到答案.
【详解】解:点,都在二次函数.的图象上,
是方程,
,
点,纵坐标相等,
,
即,
点,都在二次函数.的图象上,
,
即,
.
故答案为:.
11.
【分析】由于、、是的切线,则,,求出的长即可求出的长.本题考查了切线长定理,两次运用切线长定理并利用等式的性质是解题的关键.
【详解】解:、为的切线,
,
、为的切线,
,
.
故答案为:4.
12./
【分析】本题主要考查圆的性质,平行四边形的性质,勾股定理,熟练掌握点的运动轨迹是解题的关键.设的中点为,连接,易知当点在上时,的值最小,过点作,交的延长线于点,根据勾股定理求出,即可得到答案.
【详解】解:,
,
,
,
,
点的轨迹是以为直径的圆的一部分.
设的中点为,连接,易知当点在上时,的值最小,过点作,交的延长线于点,
则,
,
,
,
,
.
故答案为:.
13.5
【分析】本题考查垂径定理,勾股定理.设圆的半径为,利用垂径定理和勾股定理,列出方程进行求解即可.
【详解】解:连接并延长,交圆于点,,,
∵,C为弦中点,
∴,,
∴平分,
∵为的中点,
∴点,重合,
∴,,三点共线,
设圆的半径为,则:,
由勾股定理,得:,
∴,
解得:;
故答案为:5.
14./
【分析】本题考查了扇形面积和正多边形内角和的计算.根据正多边形内角和公式求出正五边形的内角和,再求出的度数,利用扇形面积公式计算即可.
【详解】解:正五边形的内角和,
,
,
故答案为:.
15.或
【分析】本题考查了根据直线和抛物线交点确定不等式的解集.解题的关键在于对知识的熟练掌握与数形结合.
由题意知,当时,则的取值范围是抛物线图象在直线图象上方对应的所有的的取值,然后数形结合求解即可.
【详解】解:由题意知,当时,则的取值范围是抛物线图象在直线图象上方对应的所有的的取值,
∵图象交于点,点,
∴当时,或,
故答案为:或.
16.①②③
【分析】本题考查了二次函数的图象性质,抛物线与与轴的交点问题,根据抛物线的开口方向向上,与轴的正半轴交于两点,得,对称轴,,即可判断①是正确的;结合,得,此时对称轴为直线,整理得,即可判断②是正确的;再因为点,点在抛物线上,且,得,即,即可判断③是正确的;先得,得,结合,整理得,函数的开口向上,则,令解得,然后再进行分类讨论,即可作答.
【详解】解:∵抛物线的开口方向向上,与轴的正半轴交于两点.
∴,对称轴,
即,
在时,随的增大而减小,且,
把代入,得,
即
∴,
故①是正确的;
∵抛物线的开口方向向上,与轴的正半轴交于两点.
且,
∴,
∴对称轴为直线,
即,
∴,
故②是正确的;
∵点,点在抛物线上,且
∴,,
∵,且对称轴为直线,且抛物线的开口方向向上,
∴
∴;
∵抛物线与轴的正半轴交于两点.
∴,
故③是正确的;
∵抛物线与轴的正半轴交于两点.
∴,
∴,
∵对称轴为直线
∴,
∵,
∴
设函数,
∵,
∴开口向上,
则
令则,
解得,
∵函数的开口向上,
则不等式的解集为.
∵,
∴,
∴,
∵,
∴,
∴.
当时,则不等式的解集为.
当时,则,故不等式的解集为.
故④是不正确的;
故答案为:①②③.
17..
【分析】本题考查了实数的运算,特殊角的三角函数值,熟练掌握运算法则是解题的关键.
先把特殊角的三角函数值代入,再计算即可.
【详解】解:
18.(1);
(2)见解析.
【分析】本题考查了二次函数的性质,二次函数的最值,二次函数图象上点的坐标的特征,解题的关键是掌握二次函数的性质.
(1)根据顶点在轴上,顶点的纵坐标是0,求出即可;
(2)把点代入解析式得到,由得到,根据二次函数的性质即可证得结论.
【详解】(1)解:根据题意得:,
解得或,
,
的值为;
(2)证明:点在抛物线上,
,
,
,
,
有最大值,
.
19.(1)
(2)
【分析】本题考查了直角三角形的性质,弧长的计算,矩形的性质,是基础知识要熟练掌握.
(1)连接,过作于,在 中,由勾股定理得出的长,进而求得的长.
(2)连接,则在直角三角形中,可求得,过点作于,在直角三角形中,可求得,则得出的长度.
【详解】(1)解:连接,过作于,
则四边形是矩形,
∴,
在中,,
∴.
(2)解:连接,
在直角三角形中,∵,
,
∴,
过点作于,在直角三角形中,
,
,
,
.
20.(1)
(2)
【分析】此题考查的是解直角三角形的应用,掌握构造直角三角形的方法和用锐角三角函数解直角三角形是解决此题的关键.
(1)作于O,根据矩形的判定,可得四边形是矩形,先求出,然后根据锐角三角函数即可求出,从而求出;
(2)过C作于点G,于点K,根据锐角三角函数,即可求出,从而求出,再求出,利用锐角三角函数即可求出,从而求出此时连杆端点D离桌面l的高度,即可求出结论.
【详解】(1)解:如图2中,作于O.
∵,
∴四边形是矩形,
∴,
,
∵成平角,
∴,
∴,
∴;
(2)解:过点C作于点G,于点K,
由题意得,,
∴在中, ,
∴,
∴,
∵,
∴,
在中,,
∴,
∴此时连杆端点D离桌面l的高度为,
∴比原来降低了.
21.(1)见解析;
(2).
【分析】(1)根据切线的判断方法,利用等腰三角形的性质,圆周角定理得出即可;
(2)根据扇形面积,三角形面积的计算方法进行计算即可.
【详解】(1)证明:连接、,
是的中点,
,
,
,
,
,
,
,
,
,
,
是的切线;
(2)解:中,,
,
在中,,,,
,
,
,
.
【点睛】本题考查扇形面积的计算,切线的判定与性质,等腰三角形的性质,解直角三角形,掌握切线的判定方法以及扇形面积的计算方法是正确解答的关键.
22.(1)r的值为
(2)②正确,定值为
【分析】(1)连接并延长,交于点,连接,等边对等角得到,内心得到是的角平分线,推出,三线合一推出,证明,得到,设,则:,进行求解即可;
(2)连接并延长,交于点,作,连接,三线合一结合勾股定理求出的长,等积法求出的长,进而求出的值,等积法求出为定值,三角函数求出,进行判断即可.
【详解】(1)解:连接并延长,交于点,连接,则:,
∴,
∵点I是的内心,
∴是的角平分线,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
设,则:,
∴,
解得:;
(2)②正确,理由如下:
连接并延长,交于点,作,连接,
∵点I是的内心,
∴点I是的三条角平分线的交点,
∵,
∴,,
∴,
∵,
∴,
∵,
∴,即:,
∴,
在中,,
∴在中,,
∵,
∴,
即:,
∴;
故为定值;
在中,,
在中,,
∴,,
∴,
∵,随着的变化而变化,不是定值,
∴不是定值.
【点睛】本题考查与三角形的内心有关的计算,相似三角形的判定和性质,解直角三角形,等腰三角形的性质,等积法求线段的长等知识点,熟练掌握内心是三角形的三条角平分线的交点,添加辅助线构造特殊图形,是解题的关键.
23.(1),喷出水的最大射程为
(2)点B的坐标为
(3)
【分析】易得的顶点A的坐标,用顶点式表示出的分析式,进而把点H的坐标代入可得a的值,取,可得的长度;
设出平移后的分析式,进而把点H的坐标代入可得m的值,取,求得相应的x的值可得抛物线与x轴的正半轴交点B的坐标;
要使洒水车行驶时喷出的水能浇灌到整个绿化带,点D与点B重合或点F在上,分别求得对应的的长,可得的取值范围.
本题考查二次函数的应用.用待定系数法求得的分析式是解决本题的关键;易错点是根据二次函数的平移规律得到的分析式;难点是判断出洒水车行驶时喷出的水能浇灌到整个绿化带时,点D或点F对应的位置.
【详解】(1)解:由题意得:点是外边缘抛物线的顶点,
设,
抛物线过点,
,
,
外边缘抛物线的函数分析式为:,
当时,,
解得:,舍去,
喷出水的最大射程为.
(2)解:由左右平移得到,
设,
经过点,
,
解得:,舍去,
,
把代入,得:
解得:,舍去,
点B的坐标为.
(3)解:要使洒水车行驶时喷出的水能浇灌到整个绿化带,
点D与点B重合或点F在上,
当点D与点B重合时,,
当点F在上时,,
解得:,不合题意,舍去,
,
,
的取值范围是
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
