小学数学冀教版六年级下第四单元 圆柱和圆锥 综合素质评价(含答案)
文档属性
| 名称 | 小学数学冀教版六年级下第四单元 圆柱和圆锥 综合素质评价(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 297.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-22 00:00:00 | ||
图片预览



文档简介
第四单元 圆柱和圆锥 综合素质评价
时间:90分钟 总分:100+10
一、填空。 (每空 2 分,共 30 分)
1.如图是一个圆柱的展开图,它的侧面积是( )dm2,表面积是( )dm2,体积是( )dm3。
2.一个圆柱和一个圆锥等底等高,如果圆柱的体积是 48 立方米,那么圆锥的体积是( )立方米;如果圆锥的体积比圆柱少 2.4 立方分米,那么圆柱的体积是( )立方分米。
3.PPR 管材是新型环保材料,具有无毒、耐腐蚀等优点。李叔叔要加工 4节长 10 米、管口直径为 0.2 分米的圆柱形 PPR 水管,至少需要( )平方米的PPR管材。如果水流的速度是 0.8米 /秒,那么 1节这种 PPR水管 5分钟可以流出( ) 升水。(管壁厚度忽略不计)
4.一个圆柱和一个圆锥的底面积之比是 1 : 3,高之比是 2 : 3,体积之比是( )。
5.如图,把一个圆柱切成若干等份后,拼成一个近似的长方体,长方体的表面积比圆柱的表面积增加了 20 cm2,圆柱的底面周长是 6.28 cm,圆柱的体积是( )cm3。
6.把一根长是 4 m,底面半径是 2 dm 的圆柱形木料截成同样长的 5个小圆柱,这5个小圆柱的表面积之和比原来增加了( )dm2。
7.有一根圆木,底面直径是 42 厘米,高是 3.5 米,这根圆木的体积是( )立方分米,将这根圆木加工成最大的方木,这根方木的体积是( )立方分米。
8.端午节吃粽子是传统习俗,不仅仅是纪念屈原,还有光“粽”耀祖、一举得“粽”的含义。天天自己动手用粽叶和糯米包了一个近似圆锥形的粽子,粽子的底面周长是 18.84 cm,高是 10 cm,这个粽子的体积是( )cm3。如果每立方厘米粽子大约需要 0.4 g 糯米,包 20 个这样的粽子,大约需要准备( )g 糯米。
9.梦梦用积木拼成如右图所示的物体,如果把圆柱和圆锥重新分开,表面积就增加 50.24 cm2。拼成的这个物体的体积是( )cm3。
二、选择。(将正确答案的序号填在括号里) (每小题 3 分,共 15 分)
1.图中的圆柱、正方体、圆锥和长方体的底面积和高均相等,下面说法正确的是( )。
A.圆锥的体积是圆柱体积的 3 倍
B.圆柱的体积比正方体的体积小一些
C.圆锥的体积是长方体体积的
D.它们的体积都可以用底面积乘高来计算
2. 如图,长方形的长是 4 cm,宽是 2 cm,分别以长边和宽边所在的直线为轴,旋转一周可以得到两个不同的圆柱。这两个圆柱的体积相比较,( )。
A.甲大 B.乙大
C.同样大 D.无法判断
3.关于下面圆柱和圆锥的体积,下列说法错误的是( )。 (单位:cm)
A.①和④的体积相等 B.②的体积是①的 3 倍
C.②的体积是④的 3 倍 D.①和③的体积相等
4. 将如图的长方形纸卷成一个圆柱的侧面,再从下面的几个图形中选一个当底面,其中容积最大的是( )。 (单位:cm)
把一个底面半径是 3 分米的圆锥,从顶点沿高切成完全相同的两部分,这时表面积增加了 12 平方分米,这个圆锥的体积是( )立方分米。
A.18.84 B.56.52 C.37.68 D.113.04
三、计算下列图形的体积。 (每小题 5 分,共 10 分)
1. 2.
四、按要求做题。 (共 15 分)
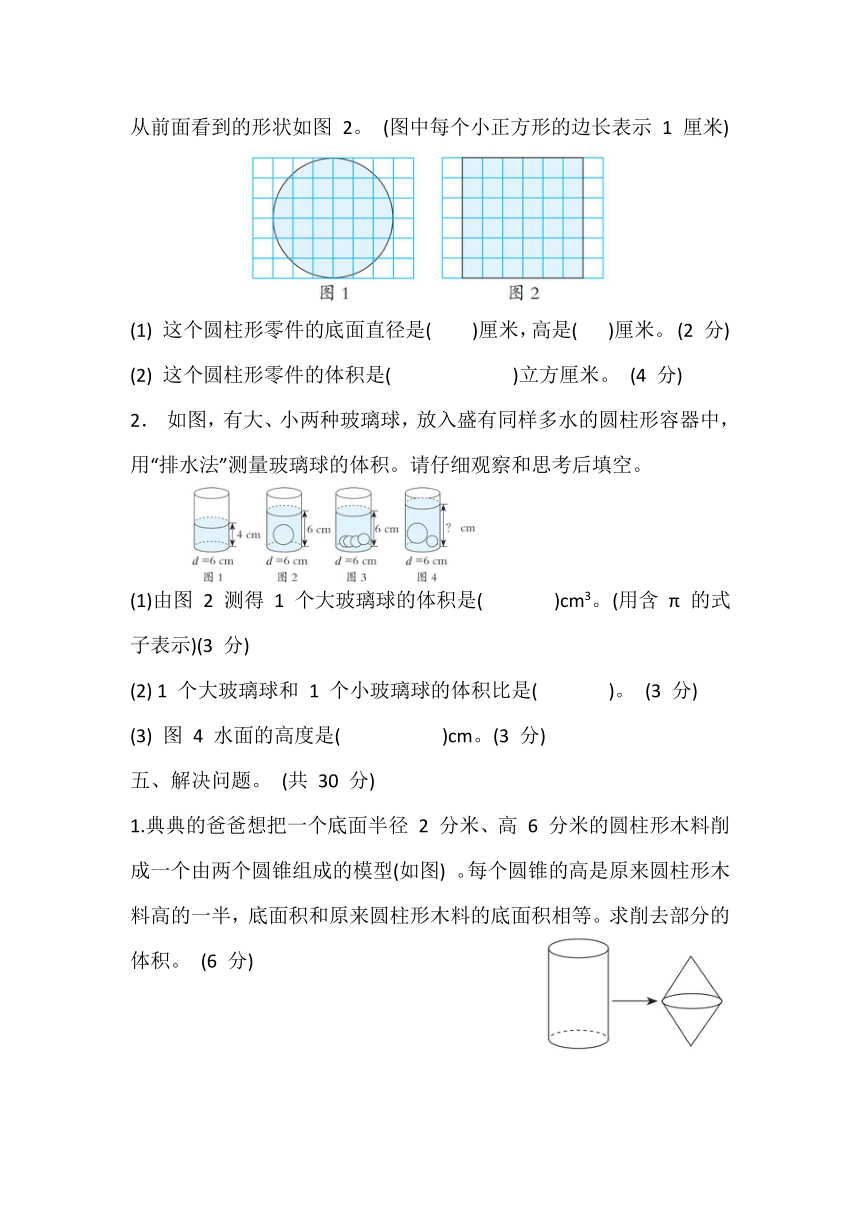
1. 德师傅设计了一个圆柱形零件,零件从上面看到的形状如图 1,从前面看到的形状如图 2。 (图中每个小正方形的边长表示 1 厘米)
(1) 这个圆柱形零件的底面直径是( )厘米,高是( )厘米。 (2 分)
(2) 这个圆柱形零件的体积是( )立方厘米。 (4 分)
2. 如图,有大、小两种玻璃球,放入盛有同样多水的圆柱形容器中,用“排水法”测量玻璃球的体积。请仔细观察和思考后填空。
(1)由图 2 测得 1 个大玻璃球的体积是( )cm3。 (用含 π 的式子表示)(3 分)
(2) 1 个大玻璃球和 1 个小玻璃球的体积比是( )。 (3 分)
(3) 图 4 水面的高度是( )cm。(3 分)
五、解决问题。 (共 30 分)
1.典典的爸爸想把一个底面半径 2 分米、高 6 分米的圆柱形木料削成一个由两个圆锥组成的模型(如图) 。每个圆锥的高是原来圆柱形木料高的一半,底面积和原来圆柱形木料的底面积相等。求削去部分的体积。 (6 分)
2一家饮料生产厂新研发一款沙棘汁,想用圆柱形易拉罐做包装,从易拉罐的外面量,底面半径是 3 厘米,高是 18 厘米,易拉罐侧面下方印有“净含量 510 毫升”的字样,请计算说明生产厂是否欺骗了消费者。 (6 分)
3.竹编文化在我国有着悠久的历史。劳动实践课上六(3)班同学学习编织竹筐,第一小组的同学用竹条编织了一个无盖的圆柱形竹筐。竹筐的直径是 40 厘米,高是 60 厘米,竹条的宽是 2 厘米。
(1) 如果给这个竹筐外部四周贴上彩纸,那么需要准备多少平方厘米的彩纸? (不计接缝)(5 分)
(2) 龙龙想用这个竹筐来种植一些花草,他把一堆底面积是 942 平方厘米,高是 40厘米的近似圆锥形的沙土倒进去。此时竹筐里的沙土有多高? (5 分)
4. 为了测量一个空瓶子的容积,典典进行了如下实验。
①测量出整个瓶子的高度是 30 cm。②测量出瓶身圆柱部分的内直径是 8 cm。③给瓶子里注入一些水,把瓶子正放时,测量出水的高度是 12 cm。④把瓶盖拧紧后倒置,此时水的高度是 20 cm。
(1)要算出这个瓶子的容积,需要知道( )。 (填序号)(2 分)
(2)请根据选出的信息,求出这个瓶子的容积。 (6 分)
附加题:天才的你,试一试。(10分)
古希腊著名的数学家阿基米德是历史上杰出的数学家之一。在他众多的科学发现中,他自己最为满意的是“圆柱容球定理”。如图,把一个球正好放在一个圆柱形容器中(容器含有上、下底) ,球的直径与圆柱的高和底面直径相等,此时球的体积正好是圆柱体积的 ,球的表面积也正好是圆柱表面积的 ,求出图中球的表面积和体积。
参考答案
一、1.62.8 87.92 62.8
2.16 3.6
3.2.512 75.36
4.2 ∶ 3
5.31.4
6.100.48
7.484.659 308.7
94.2 753.6
9.200.96
二、1.C 2.B 3.D 4.A 5.A
三、1.3.14×(20÷2) 2×6 +×3.14×(20÷2) 2×3 = 2198(m3)
2.3.14×(12÷2) 2×20÷2 = 1130.4(cm3)
四、1.(1)6 6
(2)169.56
2.(1)18π (2)4:1(3)6.5
五、1.3.14×22×6× (1- )= 50.24(立方分米)
答: 削去部分的体积是 50.24 立方分米。
2.3.14×32×18 = 508.68(立方厘米)
508.68 立方厘米 = 508.68 毫升
508.68 毫升﹤ 510 毫升
答: 生产厂欺骗了消费者。
(1)3.14×40×60 = 7536(平方厘米)
答: 需要准备 7536 平方厘米的彩纸。
(2)942×40× ÷[3.14× (40÷2) 2]=10(厘米)
答: 此时竹筐里的沙土有 10 厘米高。
(1)①②③④
(2)3.14×(8÷2) 2× [ 12 +(30 - 20)]=1105.28(cm3)
1105.28 cm3 = 1105.28 mL
答: 这个瓶子的容积是 1105.28 mL。
挑战题:表面积: ×[ 3.14× (6÷2) 2× 2 + 3.14×6×6]= 113.04(cm2)
体积: × 3.14× (6÷2) 2× 6 = 113.04(cm3)
答: 图中球的表面积是113.04 cm2,体积是113.04 cm3。
时间:90分钟 总分:100+10
一、填空。 (每空 2 分,共 30 分)
1.如图是一个圆柱的展开图,它的侧面积是( )dm2,表面积是( )dm2,体积是( )dm3。
2.一个圆柱和一个圆锥等底等高,如果圆柱的体积是 48 立方米,那么圆锥的体积是( )立方米;如果圆锥的体积比圆柱少 2.4 立方分米,那么圆柱的体积是( )立方分米。
3.PPR 管材是新型环保材料,具有无毒、耐腐蚀等优点。李叔叔要加工 4节长 10 米、管口直径为 0.2 分米的圆柱形 PPR 水管,至少需要( )平方米的PPR管材。如果水流的速度是 0.8米 /秒,那么 1节这种 PPR水管 5分钟可以流出( ) 升水。(管壁厚度忽略不计)
4.一个圆柱和一个圆锥的底面积之比是 1 : 3,高之比是 2 : 3,体积之比是( )。
5.如图,把一个圆柱切成若干等份后,拼成一个近似的长方体,长方体的表面积比圆柱的表面积增加了 20 cm2,圆柱的底面周长是 6.28 cm,圆柱的体积是( )cm3。
6.把一根长是 4 m,底面半径是 2 dm 的圆柱形木料截成同样长的 5个小圆柱,这5个小圆柱的表面积之和比原来增加了( )dm2。
7.有一根圆木,底面直径是 42 厘米,高是 3.5 米,这根圆木的体积是( )立方分米,将这根圆木加工成最大的方木,这根方木的体积是( )立方分米。
8.端午节吃粽子是传统习俗,不仅仅是纪念屈原,还有光“粽”耀祖、一举得“粽”的含义。天天自己动手用粽叶和糯米包了一个近似圆锥形的粽子,粽子的底面周长是 18.84 cm,高是 10 cm,这个粽子的体积是( )cm3。如果每立方厘米粽子大约需要 0.4 g 糯米,包 20 个这样的粽子,大约需要准备( )g 糯米。
9.梦梦用积木拼成如右图所示的物体,如果把圆柱和圆锥重新分开,表面积就增加 50.24 cm2。拼成的这个物体的体积是( )cm3。
二、选择。(将正确答案的序号填在括号里) (每小题 3 分,共 15 分)
1.图中的圆柱、正方体、圆锥和长方体的底面积和高均相等,下面说法正确的是( )。
A.圆锥的体积是圆柱体积的 3 倍
B.圆柱的体积比正方体的体积小一些
C.圆锥的体积是长方体体积的
D.它们的体积都可以用底面积乘高来计算
2. 如图,长方形的长是 4 cm,宽是 2 cm,分别以长边和宽边所在的直线为轴,旋转一周可以得到两个不同的圆柱。这两个圆柱的体积相比较,( )。
A.甲大 B.乙大
C.同样大 D.无法判断
3.关于下面圆柱和圆锥的体积,下列说法错误的是( )。 (单位:cm)
A.①和④的体积相等 B.②的体积是①的 3 倍
C.②的体积是④的 3 倍 D.①和③的体积相等
4. 将如图的长方形纸卷成一个圆柱的侧面,再从下面的几个图形中选一个当底面,其中容积最大的是( )。 (单位:cm)
把一个底面半径是 3 分米的圆锥,从顶点沿高切成完全相同的两部分,这时表面积增加了 12 平方分米,这个圆锥的体积是( )立方分米。
A.18.84 B.56.52 C.37.68 D.113.04
三、计算下列图形的体积。 (每小题 5 分,共 10 分)
1. 2.
四、按要求做题。 (共 15 分)
1. 德师傅设计了一个圆柱形零件,零件从上面看到的形状如图 1,从前面看到的形状如图 2。 (图中每个小正方形的边长表示 1 厘米)
(1) 这个圆柱形零件的底面直径是( )厘米,高是( )厘米。 (2 分)
(2) 这个圆柱形零件的体积是( )立方厘米。 (4 分)
2. 如图,有大、小两种玻璃球,放入盛有同样多水的圆柱形容器中,用“排水法”测量玻璃球的体积。请仔细观察和思考后填空。
(1)由图 2 测得 1 个大玻璃球的体积是( )cm3。 (用含 π 的式子表示)(3 分)
(2) 1 个大玻璃球和 1 个小玻璃球的体积比是( )。 (3 分)
(3) 图 4 水面的高度是( )cm。(3 分)
五、解决问题。 (共 30 分)
1.典典的爸爸想把一个底面半径 2 分米、高 6 分米的圆柱形木料削成一个由两个圆锥组成的模型(如图) 。每个圆锥的高是原来圆柱形木料高的一半,底面积和原来圆柱形木料的底面积相等。求削去部分的体积。 (6 分)
2一家饮料生产厂新研发一款沙棘汁,想用圆柱形易拉罐做包装,从易拉罐的外面量,底面半径是 3 厘米,高是 18 厘米,易拉罐侧面下方印有“净含量 510 毫升”的字样,请计算说明生产厂是否欺骗了消费者。 (6 分)
3.竹编文化在我国有着悠久的历史。劳动实践课上六(3)班同学学习编织竹筐,第一小组的同学用竹条编织了一个无盖的圆柱形竹筐。竹筐的直径是 40 厘米,高是 60 厘米,竹条的宽是 2 厘米。
(1) 如果给这个竹筐外部四周贴上彩纸,那么需要准备多少平方厘米的彩纸? (不计接缝)(5 分)
(2) 龙龙想用这个竹筐来种植一些花草,他把一堆底面积是 942 平方厘米,高是 40厘米的近似圆锥形的沙土倒进去。此时竹筐里的沙土有多高? (5 分)
4. 为了测量一个空瓶子的容积,典典进行了如下实验。
①测量出整个瓶子的高度是 30 cm。②测量出瓶身圆柱部分的内直径是 8 cm。③给瓶子里注入一些水,把瓶子正放时,测量出水的高度是 12 cm。④把瓶盖拧紧后倒置,此时水的高度是 20 cm。
(1)要算出这个瓶子的容积,需要知道( )。 (填序号)(2 分)
(2)请根据选出的信息,求出这个瓶子的容积。 (6 分)
附加题:天才的你,试一试。(10分)
古希腊著名的数学家阿基米德是历史上杰出的数学家之一。在他众多的科学发现中,他自己最为满意的是“圆柱容球定理”。如图,把一个球正好放在一个圆柱形容器中(容器含有上、下底) ,球的直径与圆柱的高和底面直径相等,此时球的体积正好是圆柱体积的 ,球的表面积也正好是圆柱表面积的 ,求出图中球的表面积和体积。
参考答案
一、1.62.8 87.92 62.8
2.16 3.6
3.2.512 75.36
4.2 ∶ 3
5.31.4
6.100.48
7.484.659 308.7
94.2 753.6
9.200.96
二、1.C 2.B 3.D 4.A 5.A
三、1.3.14×(20÷2) 2×6 +×3.14×(20÷2) 2×3 = 2198(m3)
2.3.14×(12÷2) 2×20÷2 = 1130.4(cm3)
四、1.(1)6 6
(2)169.56
2.(1)18π (2)4:1(3)6.5
五、1.3.14×22×6× (1- )= 50.24(立方分米)
答: 削去部分的体积是 50.24 立方分米。
2.3.14×32×18 = 508.68(立方厘米)
508.68 立方厘米 = 508.68 毫升
508.68 毫升﹤ 510 毫升
答: 生产厂欺骗了消费者。
(1)3.14×40×60 = 7536(平方厘米)
答: 需要准备 7536 平方厘米的彩纸。
(2)942×40× ÷[3.14× (40÷2) 2]=10(厘米)
答: 此时竹筐里的沙土有 10 厘米高。
(1)①②③④
(2)3.14×(8÷2) 2× [ 12 +(30 - 20)]=1105.28(cm3)
1105.28 cm3 = 1105.28 mL
答: 这个瓶子的容积是 1105.28 mL。
挑战题:表面积: ×[ 3.14× (6÷2) 2× 2 + 3.14×6×6]= 113.04(cm2)
体积: × 3.14× (6÷2) 2× 6 = 113.04(cm3)
答: 图中球的表面积是113.04 cm2,体积是113.04 cm3。
