2025年山东省济南长清区七年级下学期数学期中考试试题(含答案)
文档属性
| 名称 | 2025年山东省济南长清区七年级下学期数学期中考试试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 289.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-22 19:17:16 | ||
图片预览


文档简介
七年级下学期数学期中试题
本试卷分第 Ⅰ 卷(选择题)和第 Ⅱ 卷(非选择题)两部分。本试题共 8 页,满分 150 分,考试时间为 120 分钟。
答卷前请考生务必将自己的姓名、座号和准考证号填写在答题卡上,并同时将考点、姓名、准考证号和座号填在试卷规定的位置。考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷 选择题(共 40 分)
一、选择题(本题共 10 个小题,满分 40 分。在每小题给出的选项中,只有一项是符合题目要求的)
1.在中国科学院研发出新型的工业纳米机器人,其大小约为 0.00000007m,则 0.00000007m 用科学记数法表示为( )
A. 70×10 9m B. 0.7×10 7m C. 7×10 8m D. 7×108m
2.下列选项中,属于必然事件的是( )
A. 太阳从东方升起 B. 掷一次骰子,向上的一面是 6 点
C. 经过某一有交通信号灯的路口,遇到红灯 D. 从装有多个白球的箱子里取出两个红球
3.下列计算正确的是( )
A. 5a 2a=3 B. (a2)3=a6 C. (2b)2=2b2 D. a6÷a2=a3
4.如图,直线 l分别交 AB、CD于点 E、F,若 AB∥CD,∠1=40 ,则∠2的度数为( )
A. 120 B. 140 C. 150 D. 160
5.如图,斑马线的作用是为了引导行人安全地通过马路。小丽站在点 A处,她觉得沿 AP走过斑马线到达马路边 BC更节省时间,这一想法体现的数学依据是( )
A. 两点之间,线段最短 B. 两点确定一条直线
C. 过一点有且只有一条直线与已知直线垂直 D. 垂线段最短
6.若 4x2+kx+9是完全平方式,则 k的值是( )
A. 6 B. ±12 C. ±6 D. 6
7.如图,下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠5;④∠1+∠ACE=180 ;⑤∠5=∠D。其中,能判定 AD∥BE的条件有( )
A. 5个 B. 4个 C. 3个 D. 2个
8.为迎接春节到来,某商场规定:购物满 88 元以上都可以获得一次转动转盘的机会。当转盘停止时,指针指向哪个区域顾客就获得对应的奖品。转动转盘若干次,其中指针落入优胜奖区域的频率如图②所示,则转盘中优胜奖区域的圆心角∠AOB的度数近似为( )
A. 72 B. 90 C. 54 D. 20
9.已知 (x+a)(x 2)=x2+x+b,则 a,b的值分别是( )
A. a= 3,b= 6 B. a=3,b=6 C. a= 3,b=6 D. a=3,b= 6
10.根据 (x 1)(x+1)=x2 1,(x 1)(x2+x+1)=x3 1,(x 1)(x3+x2+x+1)=x4 1,(x 1)(x4+x3+x2+x+1)=x5 1...
...的规律,则 22025+22024+22023+...+23+22+21+1的个位数字是( )
A. 3 B. 5 C. 7 D. 1
第 Ⅱ 卷 非选择题(共 110 分)
二、填空题(本题共 5 个小题,满分 20 分)
11. ( 2a2)3= 。
12. 飞镖游戏板中每一块小正方形除颜色外都相同。小亮每次投掷飞镖均扎在该飞镖游戏板上,且扎在飞镖板上任意点处的机会是均等的。则小亮随机投掷一次飞镖,飞镖扎在阴影区域的概率是 。
13. 如果一个角的余角比这个角少 30 ,则这个角的度数是______°。
14. 把一张长方形纸片 ABCD沿EF折叠后,D、C分别在M、N的位置上,EM与 BC的交点为 G,若 ∠EFG=63 ,则∠2= °。
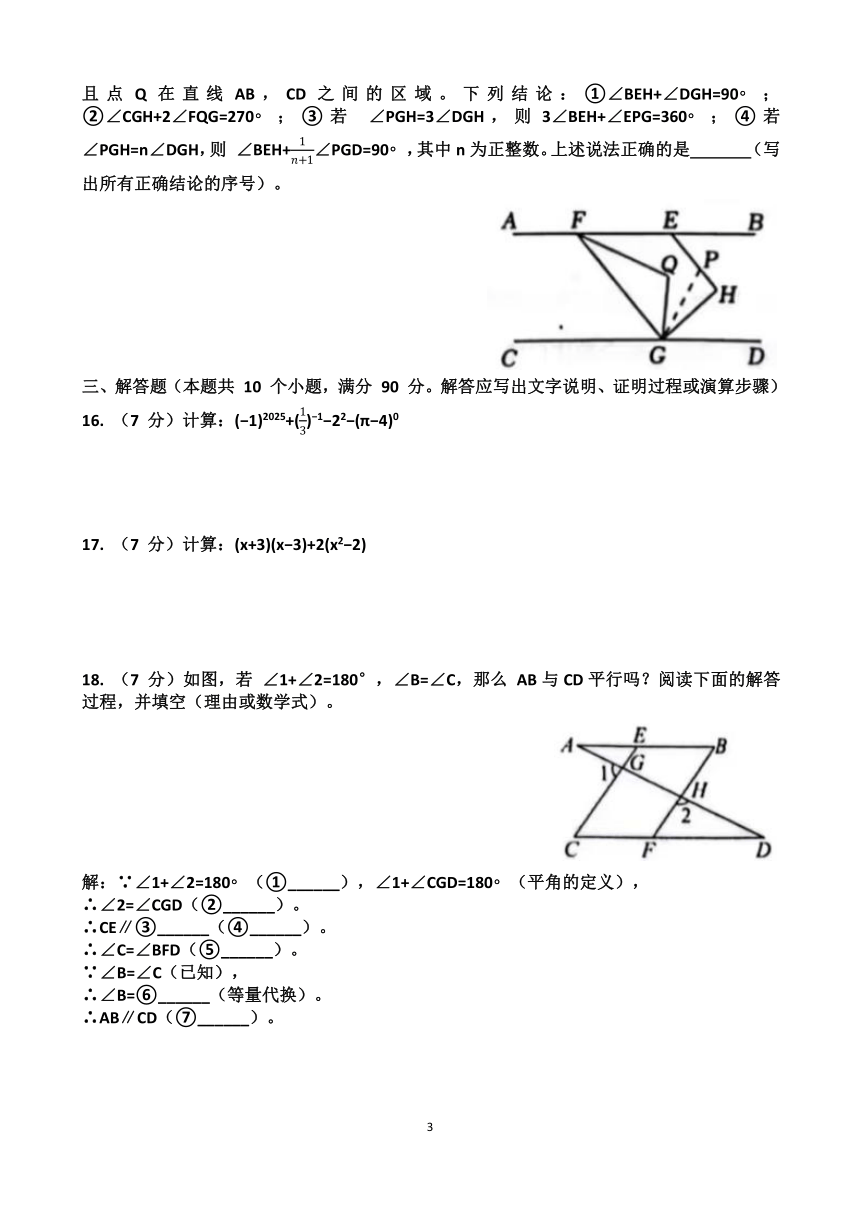
15.如图,AB∥CD,点E,F在直线AB上(F在E的左侧),点G在直线CD上,EH⊥HG,垂足为H,P为线段 EH上的一动点,连接GP,GF,∠FGH与∠BFG的角平分线交于点Q,且点Q在直线AB,CD之间的区域。下列结论:①∠BEH+∠DGH=90 ;②∠CGH+2∠FQG=270 ;③若 ∠PGH=3∠DGH,则3∠BEH+∠EPG=360 ;④若 ∠PGH=n∠DGH,则 ∠BEH+∠PGD=90 ,其中n为正整数。上述说法正确的是 (写出所有正确结论的序号)。
三、解答题(本题共 10 个小题,满分 90 分。解答应写出文字说明、证明过程或演算步骤)
16. (7 分)计算:( 1)2025+() 1 22 (π 4)0
17. (7 分)计算:(x+3)(x 3)+2(x2 2)
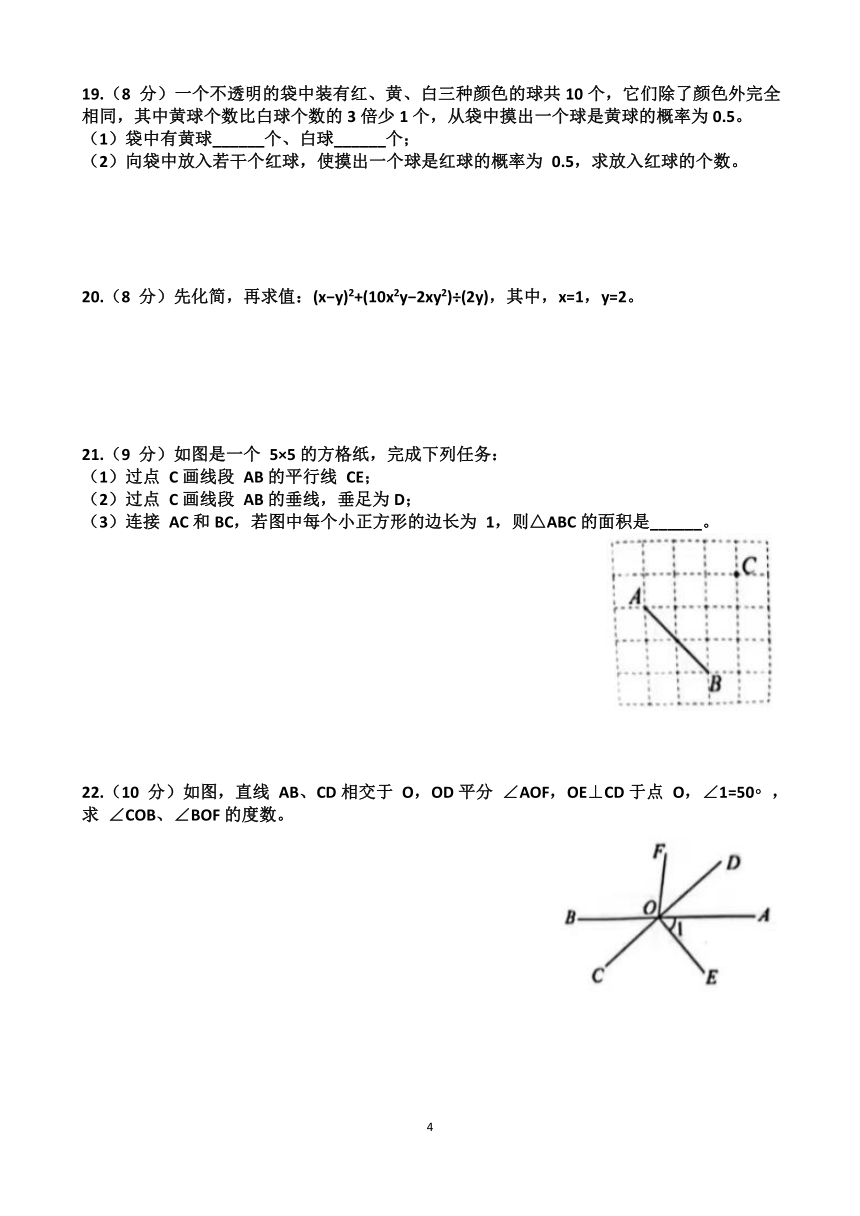
18. (7 分)如图,若 ∠1+∠2=180°,∠B=∠C,那么 AB与CD平行吗?阅读下面的解答过程,并填空(理由或数学式)。
解:∵∠1+∠2=180 (①______),∠1+∠CGD=180 (平角的定义),
∴∠2=∠CGD(②______)。
∴CE∥③______(④______)。
∴∠C=∠BFD(⑤______)。
∵∠B=∠C(已知),
∴∠B=⑥______(等量代换)。
∴AB∥CD(⑦______)。
19.(8 分)一个不透明的袋中装有红、黄、白三种颜色的球共10个,它们除了颜色外完全相同,其中黄球个数比白球个数的3倍少1个,从袋中摸出一个球是黄球的概率为0.5。
(1)袋中有黄球______个、白球______个;
(2)向袋中放入若干个红球,使摸出一个球是红球的概率为 0.5,求放入红球的个数。
20.(8 分)先化简,再求值:(x y)2+(10x2y 2xy2)÷(2y),其中,x=1,y=2。
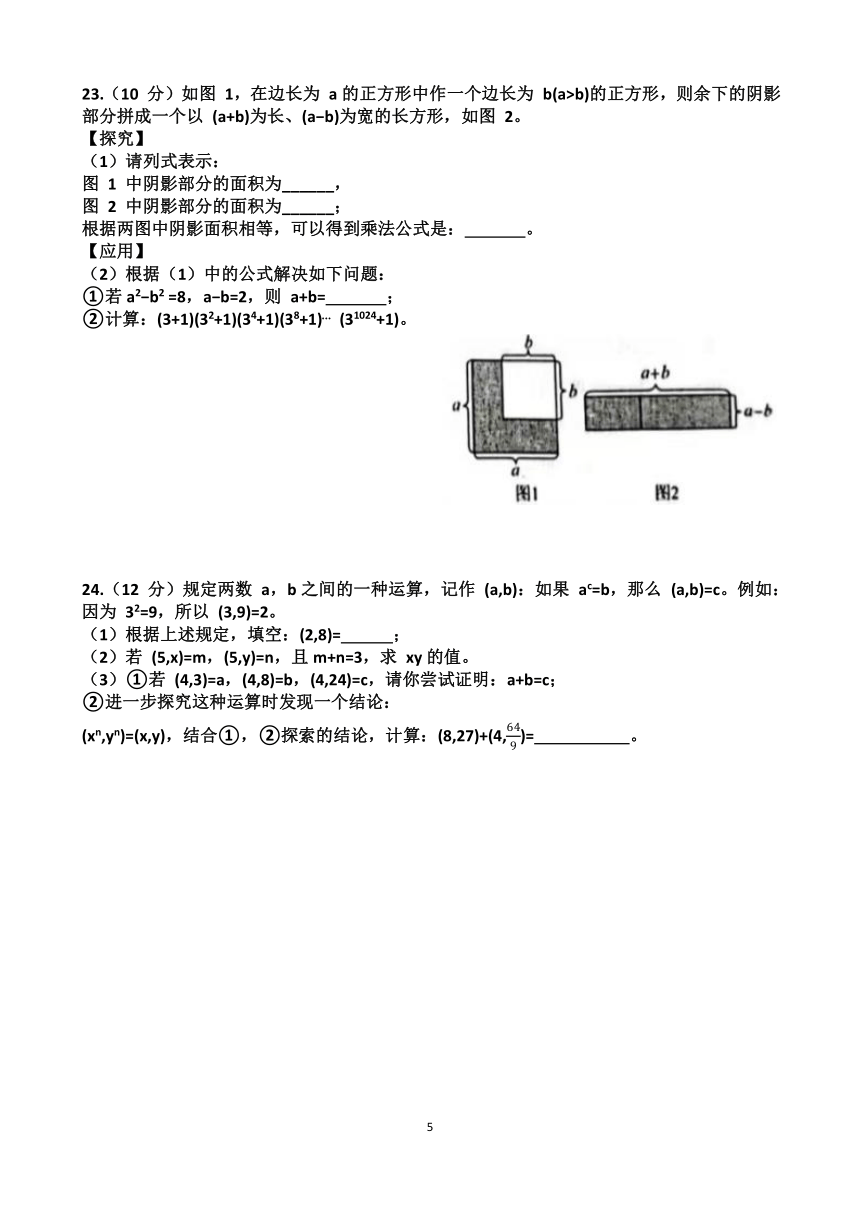
21.(9 分)如图是一个 5×5的方格纸,完成下列任务:
(1)过点 C画线段 AB的平行线 CE;
(2)过点 C画线段 AB的垂线,垂足为D;
(3)连接 AC和BC,若图中每个小正方形的边长为 1,则△ABC的面积是______。
22.(10 分)如图,直线 AB、CD相交于 O,OD平分 ∠AOF,OE⊥CD于点 O,∠1=50 ,求 ∠COB、∠BOF的度数。
23.(10 分)如图 1,在边长为 a的正方形中作一个边长为 b(a>b)的正方形,则余下的阴影部分拼成一个以 (a+b)为长、(a b)为宽的长方形,如图 2。
【探究】
(1)请列式表示:
图 1 中阴影部分的面积为______,
图 2 中阴影部分的面积为______;
根据两图中阴影面积相等,可以得到乘法公式是: 。
【应用】
(2)根据(1)中的公式解决如下问题:
①若a2 b2 =8,a b=2,则 a+b= ;
②计算:(3+1)(32+1)(34+1)(38+1) (31024+1)。
24.(12 分)规定两数 a,b之间的一种运算,记作 (a,b):如果 ac=b,那么 (a,b)=c。例如:因为 32=9,所以 (3,9)=2。
(1)根据上述规定,填空:(2,8)= ;
(2)若 (5,x)=m,(5,y)=n,且m+n=3,求 xy的值。
(3)①若 (4,3)=a,(4,8)=b,(4,24)=c,请你尝试证明:a+b=c;
②进一步探究这种运算时发现一个结论:
(xn,yn)=(x,y),结合①,②探索的结论,计算:(8,27)+(4,)= 。
25.(12 分)已知直线 AB∥CD,在三角形纸板 EFG中,∠F=90 。
(1)将三角形 EFG按如图 1 放置,点E和点G分别在直线 AB、CD上,若∠DGF=25 ,则∠AEF=_____°;
(2)将三角形 EFG按如图 2 放置,点 E和点 G分别在直线 AB、CD上,GF交 AB于点H,若 ∠DGF=α,∠BEF=β。试求 α、β之间的数量关系;
(3)在图 2 中,若 ∠AEF=20 ,∠AEG=40 ,将三角形 EFH绕点 F以每秒 10 的速度顺时针旋转一周,设运动时间为 t秒。在旋转过程中,当旋转后的三角形EFH的一条直角边与 GE平行时,求出相应 t 的值。(直接写出答案)
答案
一、选择题(本题共 10 个小题,满分 40 分。在每小题给出的选项中,只有一项是符合题目要求的)
1.在中国科学院研发出新型的工业纳米机器人,其大小约为 0.00000007m,则 0.00000007m 用科学记数法表示为( C )
A. 70×10 9m B. 0.7×10 7m C. 7×10 8m D. 7×108m
2.下列选项中,属于必然事件的是( A )
A. 太阳从东方升起 B. 掷一次骰子,向上的一面是 6 点
C. 经过某一有交通信号灯的路口,遇到红灯 D. 从装有多个白球的箱子里取出两个红球
3.下列计算正确的是( B )
A. 5a 2a=3 B. (a2)3=a6 C. (2b)2=2b2 D. a6÷a2=a3
4.如图,直线 l分别交 AB、CD于点 E、F,若 AB∥CD,∠1=40 ,则∠2的度数为( B )
A. 120 B. 140 C. 150 D. 160
5.如图,斑马线的作用是为了引导行人安全地通过马路。小丽站在点 A处,她觉得沿 AP走过斑马线到达马路边 BC更节省时间,这一想法体现的数学依据是( D )
A. 两点之间,线段最短 B. 两点确定一条直线
C. 过一点有且只有一条直线与已知直线垂直 D. 垂线段最短
6.若 4x2+kx+9是完全平方式,则 k的值是( B )
A. 6 B. ±12 C. ±6 D. 6
7.如图,下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠5;④∠1+∠ACE=180 ;⑤∠5=∠D。其中,能判定 AD∥BE的条件有( C )
A. 5个 B. 4个 C. 3个 D. 2个
8.为迎接春节到来,某商场规定:购物满 88 元以上都可以获得一次转动转盘的机会。当转盘停止时,指针指向哪个区域顾客就获得对应的奖品。转动转盘若干次,其中指针落入优胜奖区域的频率如图②所示,则转盘中优胜奖区域的圆心角∠AOB的度数近似为( A )
A. 72 B. 90 C. 54 D. 20
9.已知 (x+a)(x 2)=x2+x+b,则 a,b的值分别是( D )
A. a= 3,b= 6 B. a=3,b=6 C. a= 3,b=6 D. a=3,b= 6
10.根据 (x 1)(x+1)=x2 1,(x 1)(x2+x+1)=x3 1,(x 1)(x3+x2+x+1)=x4 1,(x 1)(x4+x3+x2+x+1)=x5 1...
...的规律,则 22025+22024+22023+...+23+22+21+1的个位数字是( A )
A. 3 B. 5 C. 7 D. 1
第 Ⅱ 卷 非选择题(共 110 分)
二、填空题(本题共 5 个小题,满分 20 分)
11. ( 2a2)3= ﹣8a6 。
12. 飞镖游戏板中每一块小正方形除颜色外都相同。小亮每次投掷飞镖均扎在该飞镖游戏板上,且扎在飞镖板上任意点处的机会是均等的。则小亮随机投掷一次飞镖,飞镖扎在阴影区域的概率是 。
13. 如果一个角的余角比这个角少 30 ,则这个角的度数是___60___°。
14. 把一张长方形纸片 ABCD沿EF折叠后,D、C分别在M、N的位置上,EM与 BC的交点为 G,若 ∠EFG=63 ,则∠2= 126 °。
15.如图,AB∥CD,点E,F在直线AB上(F在E的左侧),点G在直线CD上,EH⊥HG,垂足为H,P为线段 EH上的一动点,连接GP,GF,∠FGH与∠BFG的角平分线交于点Q,且点Q在直线AB,CD之间的区域。下列结论:①∠BEH+∠DGH=90 ;②∠CGH+2∠FQG=270 ;③若 ∠PGH=3∠DGH,则3∠BEH+∠EPG=360 ;④若 ∠PGH=n∠DGH,则 ∠BEH+∠PGD=90 ,其中n为正整数。上述说法正确的是 ①②③④ (写出所有正确结论的序号)。
三、解答题(本题共 10 个小题,满分 90 分。解答应写出文字说明、证明过程或演算步骤)
16. (7 分)计算:( 1)2025+() 1 22 (π 4)0
=﹣1+3﹣4﹣1
=﹣3
17. (7 分)计算:(x+3)(x 3)+2(x2 2)
=x2﹣9+2x2﹣4
=3x2﹣13
18. (7 分)如图,若 ∠1+∠2=180°,∠B=∠C,那么 AB与CD平行吗?阅读下面的解答过程,并填空(理由或数学式)。
解:∵∠1+∠2=180 (①___已知___),∠1+∠CGD=180 (平角的定义),
∴∠2=∠CGD(②___同角的补角相等___)。
∴CE∥③__BF____(④___同位角相等,两直线平行___)。
∴∠C=∠BFD(⑤___两直线平行,同位角相等___)。
∵∠B=∠C(已知),
∴∠B=⑥__∠BFD____(等量代换)。
∴AB∥CD(⑦___内错角相等,两直线平行___)。
19.(8 分)一个不透明的袋中装有红、黄、白三种颜色的球共10个,它们除了颜色外完全相同,其中黄球个数比白球个数的3倍少1个,从袋中摸出一个球是黄球的概率为0.5。
(1)袋中有黄球______个、白球______个;
(2)向袋中放入若干个红球,使摸出一个球是红球的概率为 0.5,求放入红球的个数。
(1)黄球 5个,白球 2个:设白球 x个
∴3x 1=5
解得:x=2
(2)设放入红球 y个,
=0.5
解得:y=4
20.(8 分)先化简,再求值:(x y)2+(10x2y 2xy2)÷(2y),其中,x=1,y=2。
解原式=x2﹣2xy+y2+5x2﹣xy
=6x2﹣3xy+y2
将x=1,y=2代入原式得6×1﹣3×1×2+4=4
21.(9 分)如图是一个 5×5的方格纸,完成下列任务:
(1)过点 C画线段 AB的平行线 CE;
(2)过点 C画线段 AB的垂线,垂足为D;
(3)连接 AC和BC,若图中每个小正方形的边长为 1,则△ABC的面积是______。
(1)略
(2)略
(3)3.5
22.(10 分)如图,直线 AB、CD相交于 O,OD平分 ∠AOF,OE⊥CD于点 O,∠1=50 ,求 ∠COB、∠BOF的度数。
解:∵OE⊥CD,∠1=50
∴∠AOD=90 50 =40 ,∠COB=∠AOD=40
∵OD平分∠AOF
∴∠AOF=80
∴∠BOF=180 80 =100
23.(10 分)如图 1,在边长为 a的正方形中作一个边长为 b(a>b)的正方形,则余下的阴影部分拼成一个以 (a+b)为长、(a b)为宽的长方形,如图 2。
【探究】
(1)请列式表示:
图 1 中阴影部分的面积为______,
图 2 中阴影部分的面积为______;
根据两图中阴影面积相等,可以得到乘法公式是: 。
【应用】
(2)根据(1)中的公式解决如下问题:
①若a2 b2 =8,a b=2,则 a+b= ;
②计算:(3+1)(32+1)(34+1)(38+1) (31024+1)。
1)a2 b2;(a+b)(a b);a2 b2=(a+b)(a b)。
(2)①a+b=4:
∵a2 b2=(a+b)(a b)=8,a b=2
∴a+b=4
②原式==
24.(12 分)规定两数 a,b之间的一种运算,记作 (a,b):如果 ac=b,那么 (a,b)=c。例如:因为 32=9,所以 (3,9)=2。
(1)根据上述规定,填空:(2,8)= ;
(2)若 (5,x)=m,(5,y)=n,且m+n=3,求 xy的值。
(3)①若 (4,3)=a,(4,8)=b,(4,24)=c,请你尝试证明:a+b=c;
②进一步探究这种运算时发现一个结论:
(xn,yn)=(x,y),结合①,②探索的结论,计算:(8,27)+(4,)= 。
(1)3:23=8,(2,8)=3。
(2)(5,x)=m,(5,y)=n,5m=x,5n=y,xy=5 m+n=53=125。
(3)①4a=3,4b=8
4a×4b=24=4c
∴a+b=c
②3:
(8,27)=(23,33)=(2,3),(4,)=(2,)
(2,3)+(2,)=3
25.(12 分)已知直线 AB∥CD,在三角形纸板 EFG中,∠F=90 。
(1)将三角形 EFG按如图 1 放置,点E和点G分别在直线 AB、CD上,若∠DGF=25 ,则∠AEF=_____°;
(2)将三角形 EFG按如图 2 放置,点 E和点 G分别在直线 AB、CD上,GF交 AB于点H,若 ∠DGF=α,∠BEF=β。试求 α、β之间的数量关系;
(3)在图 2 中,若 ∠AEF=20 ,∠AEG=40 ,将三角形 EFH绕点 F以每秒 10 的速度顺时针旋转一周,设运动时间为 t秒。在旋转过程中,当旋转后的三角形EFH的一条直角边与 GE平行时,求出相应 t 的值。(直接写出答案)
(1)65
过 F作 FH∥AB
∴∠DGF=∠GFH=25
∴∠EFH=90 25 =65
∴∠AEF=∠EFH=65
(2)α+β=270
过 F作 FM∥AB
∴∠BEF+∠EFM=180 ,∠DGF+∠GFM=180
∵∠EFM+∠GFM=90
∴∠BEF+∠DGF=270
即 α+β=270
(3)t=2、11、20、29
当 EF边与 GE平行时t=2;
当 FG边与 GE平行时,t= =11;
继续旋转,t=20;t=29。
本试卷分第 Ⅰ 卷(选择题)和第 Ⅱ 卷(非选择题)两部分。本试题共 8 页,满分 150 分,考试时间为 120 分钟。
答卷前请考生务必将自己的姓名、座号和准考证号填写在答题卡上,并同时将考点、姓名、准考证号和座号填在试卷规定的位置。考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷 选择题(共 40 分)
一、选择题(本题共 10 个小题,满分 40 分。在每小题给出的选项中,只有一项是符合题目要求的)
1.在中国科学院研发出新型的工业纳米机器人,其大小约为 0.00000007m,则 0.00000007m 用科学记数法表示为( )
A. 70×10 9m B. 0.7×10 7m C. 7×10 8m D. 7×108m
2.下列选项中,属于必然事件的是( )
A. 太阳从东方升起 B. 掷一次骰子,向上的一面是 6 点
C. 经过某一有交通信号灯的路口,遇到红灯 D. 从装有多个白球的箱子里取出两个红球
3.下列计算正确的是( )
A. 5a 2a=3 B. (a2)3=a6 C. (2b)2=2b2 D. a6÷a2=a3
4.如图,直线 l分别交 AB、CD于点 E、F,若 AB∥CD,∠1=40 ,则∠2的度数为( )
A. 120 B. 140 C. 150 D. 160
5.如图,斑马线的作用是为了引导行人安全地通过马路。小丽站在点 A处,她觉得沿 AP走过斑马线到达马路边 BC更节省时间,这一想法体现的数学依据是( )
A. 两点之间,线段最短 B. 两点确定一条直线
C. 过一点有且只有一条直线与已知直线垂直 D. 垂线段最短
6.若 4x2+kx+9是完全平方式,则 k的值是( )
A. 6 B. ±12 C. ±6 D. 6
7.如图,下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠5;④∠1+∠ACE=180 ;⑤∠5=∠D。其中,能判定 AD∥BE的条件有( )
A. 5个 B. 4个 C. 3个 D. 2个
8.为迎接春节到来,某商场规定:购物满 88 元以上都可以获得一次转动转盘的机会。当转盘停止时,指针指向哪个区域顾客就获得对应的奖品。转动转盘若干次,其中指针落入优胜奖区域的频率如图②所示,则转盘中优胜奖区域的圆心角∠AOB的度数近似为( )
A. 72 B. 90 C. 54 D. 20
9.已知 (x+a)(x 2)=x2+x+b,则 a,b的值分别是( )
A. a= 3,b= 6 B. a=3,b=6 C. a= 3,b=6 D. a=3,b= 6
10.根据 (x 1)(x+1)=x2 1,(x 1)(x2+x+1)=x3 1,(x 1)(x3+x2+x+1)=x4 1,(x 1)(x4+x3+x2+x+1)=x5 1...
...的规律,则 22025+22024+22023+...+23+22+21+1的个位数字是( )
A. 3 B. 5 C. 7 D. 1
第 Ⅱ 卷 非选择题(共 110 分)
二、填空题(本题共 5 个小题,满分 20 分)
11. ( 2a2)3= 。
12. 飞镖游戏板中每一块小正方形除颜色外都相同。小亮每次投掷飞镖均扎在该飞镖游戏板上,且扎在飞镖板上任意点处的机会是均等的。则小亮随机投掷一次飞镖,飞镖扎在阴影区域的概率是 。
13. 如果一个角的余角比这个角少 30 ,则这个角的度数是______°。
14. 把一张长方形纸片 ABCD沿EF折叠后,D、C分别在M、N的位置上,EM与 BC的交点为 G,若 ∠EFG=63 ,则∠2= °。
15.如图,AB∥CD,点E,F在直线AB上(F在E的左侧),点G在直线CD上,EH⊥HG,垂足为H,P为线段 EH上的一动点,连接GP,GF,∠FGH与∠BFG的角平分线交于点Q,且点Q在直线AB,CD之间的区域。下列结论:①∠BEH+∠DGH=90 ;②∠CGH+2∠FQG=270 ;③若 ∠PGH=3∠DGH,则3∠BEH+∠EPG=360 ;④若 ∠PGH=n∠DGH,则 ∠BEH+∠PGD=90 ,其中n为正整数。上述说法正确的是 (写出所有正确结论的序号)。
三、解答题(本题共 10 个小题,满分 90 分。解答应写出文字说明、证明过程或演算步骤)
16. (7 分)计算:( 1)2025+() 1 22 (π 4)0
17. (7 分)计算:(x+3)(x 3)+2(x2 2)
18. (7 分)如图,若 ∠1+∠2=180°,∠B=∠C,那么 AB与CD平行吗?阅读下面的解答过程,并填空(理由或数学式)。
解:∵∠1+∠2=180 (①______),∠1+∠CGD=180 (平角的定义),
∴∠2=∠CGD(②______)。
∴CE∥③______(④______)。
∴∠C=∠BFD(⑤______)。
∵∠B=∠C(已知),
∴∠B=⑥______(等量代换)。
∴AB∥CD(⑦______)。
19.(8 分)一个不透明的袋中装有红、黄、白三种颜色的球共10个,它们除了颜色外完全相同,其中黄球个数比白球个数的3倍少1个,从袋中摸出一个球是黄球的概率为0.5。
(1)袋中有黄球______个、白球______个;
(2)向袋中放入若干个红球,使摸出一个球是红球的概率为 0.5,求放入红球的个数。
20.(8 分)先化简,再求值:(x y)2+(10x2y 2xy2)÷(2y),其中,x=1,y=2。
21.(9 分)如图是一个 5×5的方格纸,完成下列任务:
(1)过点 C画线段 AB的平行线 CE;
(2)过点 C画线段 AB的垂线,垂足为D;
(3)连接 AC和BC,若图中每个小正方形的边长为 1,则△ABC的面积是______。
22.(10 分)如图,直线 AB、CD相交于 O,OD平分 ∠AOF,OE⊥CD于点 O,∠1=50 ,求 ∠COB、∠BOF的度数。
23.(10 分)如图 1,在边长为 a的正方形中作一个边长为 b(a>b)的正方形,则余下的阴影部分拼成一个以 (a+b)为长、(a b)为宽的长方形,如图 2。
【探究】
(1)请列式表示:
图 1 中阴影部分的面积为______,
图 2 中阴影部分的面积为______;
根据两图中阴影面积相等,可以得到乘法公式是: 。
【应用】
(2)根据(1)中的公式解决如下问题:
①若a2 b2 =8,a b=2,则 a+b= ;
②计算:(3+1)(32+1)(34+1)(38+1) (31024+1)。
24.(12 分)规定两数 a,b之间的一种运算,记作 (a,b):如果 ac=b,那么 (a,b)=c。例如:因为 32=9,所以 (3,9)=2。
(1)根据上述规定,填空:(2,8)= ;
(2)若 (5,x)=m,(5,y)=n,且m+n=3,求 xy的值。
(3)①若 (4,3)=a,(4,8)=b,(4,24)=c,请你尝试证明:a+b=c;
②进一步探究这种运算时发现一个结论:
(xn,yn)=(x,y),结合①,②探索的结论,计算:(8,27)+(4,)= 。
25.(12 分)已知直线 AB∥CD,在三角形纸板 EFG中,∠F=90 。
(1)将三角形 EFG按如图 1 放置,点E和点G分别在直线 AB、CD上,若∠DGF=25 ,则∠AEF=_____°;
(2)将三角形 EFG按如图 2 放置,点 E和点 G分别在直线 AB、CD上,GF交 AB于点H,若 ∠DGF=α,∠BEF=β。试求 α、β之间的数量关系;
(3)在图 2 中,若 ∠AEF=20 ,∠AEG=40 ,将三角形 EFH绕点 F以每秒 10 的速度顺时针旋转一周,设运动时间为 t秒。在旋转过程中,当旋转后的三角形EFH的一条直角边与 GE平行时,求出相应 t 的值。(直接写出答案)
答案
一、选择题(本题共 10 个小题,满分 40 分。在每小题给出的选项中,只有一项是符合题目要求的)
1.在中国科学院研发出新型的工业纳米机器人,其大小约为 0.00000007m,则 0.00000007m 用科学记数法表示为( C )
A. 70×10 9m B. 0.7×10 7m C. 7×10 8m D. 7×108m
2.下列选项中,属于必然事件的是( A )
A. 太阳从东方升起 B. 掷一次骰子,向上的一面是 6 点
C. 经过某一有交通信号灯的路口,遇到红灯 D. 从装有多个白球的箱子里取出两个红球
3.下列计算正确的是( B )
A. 5a 2a=3 B. (a2)3=a6 C. (2b)2=2b2 D. a6÷a2=a3
4.如图,直线 l分别交 AB、CD于点 E、F,若 AB∥CD,∠1=40 ,则∠2的度数为( B )
A. 120 B. 140 C. 150 D. 160
5.如图,斑马线的作用是为了引导行人安全地通过马路。小丽站在点 A处,她觉得沿 AP走过斑马线到达马路边 BC更节省时间,这一想法体现的数学依据是( D )
A. 两点之间,线段最短 B. 两点确定一条直线
C. 过一点有且只有一条直线与已知直线垂直 D. 垂线段最短
6.若 4x2+kx+9是完全平方式,则 k的值是( B )
A. 6 B. ±12 C. ±6 D. 6
7.如图,下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠5;④∠1+∠ACE=180 ;⑤∠5=∠D。其中,能判定 AD∥BE的条件有( C )
A. 5个 B. 4个 C. 3个 D. 2个
8.为迎接春节到来,某商场规定:购物满 88 元以上都可以获得一次转动转盘的机会。当转盘停止时,指针指向哪个区域顾客就获得对应的奖品。转动转盘若干次,其中指针落入优胜奖区域的频率如图②所示,则转盘中优胜奖区域的圆心角∠AOB的度数近似为( A )
A. 72 B. 90 C. 54 D. 20
9.已知 (x+a)(x 2)=x2+x+b,则 a,b的值分别是( D )
A. a= 3,b= 6 B. a=3,b=6 C. a= 3,b=6 D. a=3,b= 6
10.根据 (x 1)(x+1)=x2 1,(x 1)(x2+x+1)=x3 1,(x 1)(x3+x2+x+1)=x4 1,(x 1)(x4+x3+x2+x+1)=x5 1...
...的规律,则 22025+22024+22023+...+23+22+21+1的个位数字是( A )
A. 3 B. 5 C. 7 D. 1
第 Ⅱ 卷 非选择题(共 110 分)
二、填空题(本题共 5 个小题,满分 20 分)
11. ( 2a2)3= ﹣8a6 。
12. 飞镖游戏板中每一块小正方形除颜色外都相同。小亮每次投掷飞镖均扎在该飞镖游戏板上,且扎在飞镖板上任意点处的机会是均等的。则小亮随机投掷一次飞镖,飞镖扎在阴影区域的概率是 。
13. 如果一个角的余角比这个角少 30 ,则这个角的度数是___60___°。
14. 把一张长方形纸片 ABCD沿EF折叠后,D、C分别在M、N的位置上,EM与 BC的交点为 G,若 ∠EFG=63 ,则∠2= 126 °。
15.如图,AB∥CD,点E,F在直线AB上(F在E的左侧),点G在直线CD上,EH⊥HG,垂足为H,P为线段 EH上的一动点,连接GP,GF,∠FGH与∠BFG的角平分线交于点Q,且点Q在直线AB,CD之间的区域。下列结论:①∠BEH+∠DGH=90 ;②∠CGH+2∠FQG=270 ;③若 ∠PGH=3∠DGH,则3∠BEH+∠EPG=360 ;④若 ∠PGH=n∠DGH,则 ∠BEH+∠PGD=90 ,其中n为正整数。上述说法正确的是 ①②③④ (写出所有正确结论的序号)。
三、解答题(本题共 10 个小题,满分 90 分。解答应写出文字说明、证明过程或演算步骤)
16. (7 分)计算:( 1)2025+() 1 22 (π 4)0
=﹣1+3﹣4﹣1
=﹣3
17. (7 分)计算:(x+3)(x 3)+2(x2 2)
=x2﹣9+2x2﹣4
=3x2﹣13
18. (7 分)如图,若 ∠1+∠2=180°,∠B=∠C,那么 AB与CD平行吗?阅读下面的解答过程,并填空(理由或数学式)。
解:∵∠1+∠2=180 (①___已知___),∠1+∠CGD=180 (平角的定义),
∴∠2=∠CGD(②___同角的补角相等___)。
∴CE∥③__BF____(④___同位角相等,两直线平行___)。
∴∠C=∠BFD(⑤___两直线平行,同位角相等___)。
∵∠B=∠C(已知),
∴∠B=⑥__∠BFD____(等量代换)。
∴AB∥CD(⑦___内错角相等,两直线平行___)。
19.(8 分)一个不透明的袋中装有红、黄、白三种颜色的球共10个,它们除了颜色外完全相同,其中黄球个数比白球个数的3倍少1个,从袋中摸出一个球是黄球的概率为0.5。
(1)袋中有黄球______个、白球______个;
(2)向袋中放入若干个红球,使摸出一个球是红球的概率为 0.5,求放入红球的个数。
(1)黄球 5个,白球 2个:设白球 x个
∴3x 1=5
解得:x=2
(2)设放入红球 y个,
=0.5
解得:y=4
20.(8 分)先化简,再求值:(x y)2+(10x2y 2xy2)÷(2y),其中,x=1,y=2。
解原式=x2﹣2xy+y2+5x2﹣xy
=6x2﹣3xy+y2
将x=1,y=2代入原式得6×1﹣3×1×2+4=4
21.(9 分)如图是一个 5×5的方格纸,完成下列任务:
(1)过点 C画线段 AB的平行线 CE;
(2)过点 C画线段 AB的垂线,垂足为D;
(3)连接 AC和BC,若图中每个小正方形的边长为 1,则△ABC的面积是______。
(1)略
(2)略
(3)3.5
22.(10 分)如图,直线 AB、CD相交于 O,OD平分 ∠AOF,OE⊥CD于点 O,∠1=50 ,求 ∠COB、∠BOF的度数。
解:∵OE⊥CD,∠1=50
∴∠AOD=90 50 =40 ,∠COB=∠AOD=40
∵OD平分∠AOF
∴∠AOF=80
∴∠BOF=180 80 =100
23.(10 分)如图 1,在边长为 a的正方形中作一个边长为 b(a>b)的正方形,则余下的阴影部分拼成一个以 (a+b)为长、(a b)为宽的长方形,如图 2。
【探究】
(1)请列式表示:
图 1 中阴影部分的面积为______,
图 2 中阴影部分的面积为______;
根据两图中阴影面积相等,可以得到乘法公式是: 。
【应用】
(2)根据(1)中的公式解决如下问题:
①若a2 b2 =8,a b=2,则 a+b= ;
②计算:(3+1)(32+1)(34+1)(38+1) (31024+1)。
1)a2 b2;(a+b)(a b);a2 b2=(a+b)(a b)。
(2)①a+b=4:
∵a2 b2=(a+b)(a b)=8,a b=2
∴a+b=4
②原式==
24.(12 分)规定两数 a,b之间的一种运算,记作 (a,b):如果 ac=b,那么 (a,b)=c。例如:因为 32=9,所以 (3,9)=2。
(1)根据上述规定,填空:(2,8)= ;
(2)若 (5,x)=m,(5,y)=n,且m+n=3,求 xy的值。
(3)①若 (4,3)=a,(4,8)=b,(4,24)=c,请你尝试证明:a+b=c;
②进一步探究这种运算时发现一个结论:
(xn,yn)=(x,y),结合①,②探索的结论,计算:(8,27)+(4,)= 。
(1)3:23=8,(2,8)=3。
(2)(5,x)=m,(5,y)=n,5m=x,5n=y,xy=5 m+n=53=125。
(3)①4a=3,4b=8
4a×4b=24=4c
∴a+b=c
②3:
(8,27)=(23,33)=(2,3),(4,)=(2,)
(2,3)+(2,)=3
25.(12 分)已知直线 AB∥CD,在三角形纸板 EFG中,∠F=90 。
(1)将三角形 EFG按如图 1 放置,点E和点G分别在直线 AB、CD上,若∠DGF=25 ,则∠AEF=_____°;
(2)将三角形 EFG按如图 2 放置,点 E和点 G分别在直线 AB、CD上,GF交 AB于点H,若 ∠DGF=α,∠BEF=β。试求 α、β之间的数量关系;
(3)在图 2 中,若 ∠AEF=20 ,∠AEG=40 ,将三角形 EFH绕点 F以每秒 10 的速度顺时针旋转一周,设运动时间为 t秒。在旋转过程中,当旋转后的三角形EFH的一条直角边与 GE平行时,求出相应 t 的值。(直接写出答案)
(1)65
过 F作 FH∥AB
∴∠DGF=∠GFH=25
∴∠EFH=90 25 =65
∴∠AEF=∠EFH=65
(2)α+β=270
过 F作 FM∥AB
∴∠BEF+∠EFM=180 ,∠DGF+∠GFM=180
∵∠EFM+∠GFM=90
∴∠BEF+∠DGF=270
即 α+β=270
(3)t=2、11、20、29
当 EF边与 GE平行时t=2;
当 FG边与 GE平行时,t= =11;
继续旋转,t=20;t=29。
同课章节目录
