湖南省益阳市第六中学2015-2016学年高一3月月考数学试题
文档属性
| 名称 | 湖南省益阳市第六中学2015-2016学年高一3月月考数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 71.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-30 00:00:00 | ||
图片预览



文档简介
益阳市六中2016年上学期第一次月考
高一 数学试卷
时量:120分钟 总分:100分 命题人:李梦龙
一、选择题:共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的.(60分)
1.在①160°;②480°;③-960°;④1 530°这四个角中,属于第二象限角的是 ( ).
A.① B.①② C.①②③ D.①②③④
2.若2弧度的圆心角所对的弧长为2 cm,则这个圆心角所夹的扇形的面积是
( ).
A.4 cm2 B.2 cm2 C.4π cm2 D.1 cm2
3.函数y=cos x·tan x的值域是 ( ).
A.(-1,0)∪(0,1) B.[-1,1]
C.(-1,1) D.[-1,0]∪(0,1)
4..化简的结果是 ( )
A. B. C. D.
5.三角函数y=sin 是 ( ).
A.周期为4π的奇函数 B.周期为的奇函数
C.周期为π的偶函数 D.周期为2π的偶函数
6.已知sin=,则cos的值为 ( ).
A. B.- C.- D.
7.函数f(x)=sin-1的最小值和最小正周期分别是 ( ).
A.--1,π B.-+1,π
C.-,π D.--1,2π
8.要得到函数y=f(2x+π)的图象,只要将函数y=f(x)的图象 ( ).
A.向左平移π个单位,再把所有点的横坐标伸长到原来的2倍,纵坐标不变
B.向右平移π个单位,再把所有点的横坐标伸长到原来的2倍,纵坐标不变
C.向左平移π个单位,再把所有点的横坐标缩短到原来的,纵坐标不变
D.向右平移π个单位,再把所有点的横坐标缩短到原来的,纵坐标不变
9.函数的定义域是 ( )
A. B.
C. D.
10.函数y=2sin的图象 ( ).
A.关于原点成中心对称 B.关于y轴成轴对称
C.关于点成中心对称 D.关于直线x=成轴对称
11.函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图所示,则该函数的表达式为( ).
A.y=2sin
B.y=2sin
C.y=2sin
D.y=2sin
12.下列说法正确的是 ( ).
A.在内sin x>cos x
B.函数y=2sin的图象的一条对称轴是x=π
C.函数y=的最大值为π
D.函数y=sin 2x的图象可以由函数y=sin的图象向右平移个单位得到
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上)
13.函数y=tan的定义域为________.
14.函数y=2cos的最小正周期是4π,则ω=________.
15.若sin=-,且π16.已知tan θ=2,则=________.
三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)
17、(12分)求值或化简
(1).求值:
(2).已知α是第三角限的角,化简
18.(10分)已知sin α+3cos α=0,求sin α,cos α的值.
19.(10分))已知tan α=, 求的值.
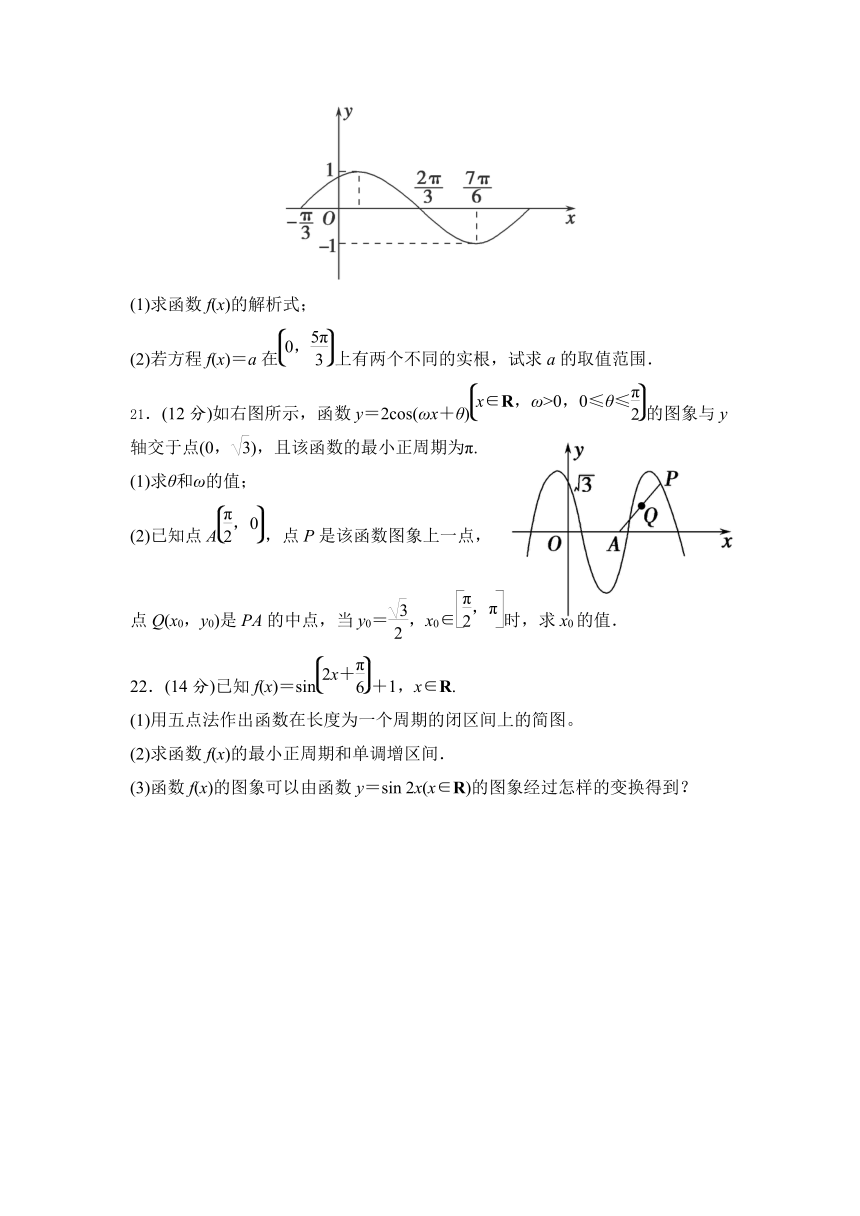
20.(12分)已知函数f(x)=Asin(ωx+φ)A>0且ω>0,0<φ<的部分图象,如图所示.
( http: / / www.21cnjy.com )
(1)求函数f(x)的解析式;
(2)若方程f(x)=a在上有两个不同的实根,试求a的取值范围.
21.(12分)如右图所示,函数y=2cos(ωx+θ)的图象与y轴交于点(0,),且该函数的最小正周期为π.
(1)求θ和ω的值;
(2)已知点A,点P是该函数图象上一点,
点Q(x0,y0)是PA的中点,当y0=,x0∈时,求x0的值.
22.(14分)已知f(x)=sin+1,x∈R.
(1)用五点法作出函数在长度为一个周期的闭区间上的简图。
(2)求函数f(x)的最小正周期和单调增区间.
(3)函数f(x)的图象可以由函数y=sin 2x(x∈R)的图象经过怎样的变换得到?
2016年上学期高一3月月考数学试题答案
一:选择题
C,D,C,B,A,B,A,C,D,C,C,C.
二:填空题
13. 14. ±
15. 16.
三.解答题
17.(1)原式= (2)原式=-2tan
18.解 ∵sin α=-3cos α.
又sin2α+cos2α=1,得(-3cos α)2+cos2α=1,
即10cos2α=1.∴cos α=±.
又由sin α=-3cos α,可知sin α与cos α异号,
∴α在第二、四象限.
①当α是第二象限角时,sin α=,cos α=-.
②当α是第四象限角时,sin α=-,cos α=.
19.原式=
==
====-3.
20.解 (1)由图象易知函数f(x)的周期为
T=4×=2π,A=1,所以ω=1.
法一 由图可知此函数的图象是由y=sin x的图象向左平移个单位得到的,故φ=,所以函数解析式为f(x)=sin.
法二 由图象知f(x)过点.
则sin=0,
∴-+φ=kπ,k∈Z.
∴φ=kπ+,k∈Z,
又∵φ∈,
∴φ=,
∴f(x)=sin.
(2)方程f(x)=a在上有两个不同的 ( http: / / www.21cnjy.com )实根等价于y=f(x)与y=a的图象在上有两个交点,在图中作y=a的图象,如图为函数f(x)=sin在上的图象,当x=0时,f(x)=,当x=时,f(x)=0,由图中可以看出有两个交点时,a∈∪(-1,0).
( http: / / www.21cnjy.com )
21.解 (1)将x=0,y=代入函数y=2cos(ωx+θ)中,得cos θ=,因为0≤θ≤,所以θ=.
由已知T=π,且ω>0,得ω===2.
(2)因为点A,Q(x0,y0)是PA的中点,
y0=,所以点P的坐标为.
又因为点P在y=2cos的图象上,且≤x0≤π,
所以cos=,且≤4x0-≤,
从而得4x0-=,或4x0-=,即x0=,或x0=.
解 (1)图略
(2)T==π,由2kπ-≤2x+≤2kπ+,k∈Z知kπ-≤x≤kπ+(k∈Z).
所以所求的单调递增区间为(k∈Z).
(2)变换情况如下:y=sin 2x
y=sin
y=sin+1
高一 数学试卷
时量:120分钟 总分:100分 命题人:李梦龙
一、选择题:共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的.(60分)
1.在①160°;②480°;③-960°;④1 530°这四个角中,属于第二象限角的是 ( ).
A.① B.①② C.①②③ D.①②③④
2.若2弧度的圆心角所对的弧长为2 cm,则这个圆心角所夹的扇形的面积是
( ).
A.4 cm2 B.2 cm2 C.4π cm2 D.1 cm2
3.函数y=cos x·tan x的值域是 ( ).
A.(-1,0)∪(0,1) B.[-1,1]
C.(-1,1) D.[-1,0]∪(0,1)
4..化简的结果是 ( )
A. B. C. D.
5.三角函数y=sin 是 ( ).
A.周期为4π的奇函数 B.周期为的奇函数
C.周期为π的偶函数 D.周期为2π的偶函数
6.已知sin=,则cos的值为 ( ).
A. B.- C.- D.
7.函数f(x)=sin-1的最小值和最小正周期分别是 ( ).
A.--1,π B.-+1,π
C.-,π D.--1,2π
8.要得到函数y=f(2x+π)的图象,只要将函数y=f(x)的图象 ( ).
A.向左平移π个单位,再把所有点的横坐标伸长到原来的2倍,纵坐标不变
B.向右平移π个单位,再把所有点的横坐标伸长到原来的2倍,纵坐标不变
C.向左平移π个单位,再把所有点的横坐标缩短到原来的,纵坐标不变
D.向右平移π个单位,再把所有点的横坐标缩短到原来的,纵坐标不变
9.函数的定义域是 ( )
A. B.
C. D.
10.函数y=2sin的图象 ( ).
A.关于原点成中心对称 B.关于y轴成轴对称
C.关于点成中心对称 D.关于直线x=成轴对称
11.函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图所示,则该函数的表达式为( ).
A.y=2sin
B.y=2sin
C.y=2sin
D.y=2sin
12.下列说法正确的是 ( ).
A.在内sin x>cos x
B.函数y=2sin的图象的一条对称轴是x=π
C.函数y=的最大值为π
D.函数y=sin 2x的图象可以由函数y=sin的图象向右平移个单位得到
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上)
13.函数y=tan的定义域为________.
14.函数y=2cos的最小正周期是4π,则ω=________.
15.若sin=-,且π
三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)
17、(12分)求值或化简
(1).求值:
(2).已知α是第三角限的角,化简
18.(10分)已知sin α+3cos α=0,求sin α,cos α的值.
19.(10分))已知tan α=, 求的值.
20.(12分)已知函数f(x)=Asin(ωx+φ)A>0且ω>0,0<φ<的部分图象,如图所示.
( http: / / www.21cnjy.com )
(1)求函数f(x)的解析式;
(2)若方程f(x)=a在上有两个不同的实根,试求a的取值范围.
21.(12分)如右图所示,函数y=2cos(ωx+θ)的图象与y轴交于点(0,),且该函数的最小正周期为π.
(1)求θ和ω的值;
(2)已知点A,点P是该函数图象上一点,
点Q(x0,y0)是PA的中点,当y0=,x0∈时,求x0的值.
22.(14分)已知f(x)=sin+1,x∈R.
(1)用五点法作出函数在长度为一个周期的闭区间上的简图。
(2)求函数f(x)的最小正周期和单调增区间.
(3)函数f(x)的图象可以由函数y=sin 2x(x∈R)的图象经过怎样的变换得到?
2016年上学期高一3月月考数学试题答案
一:选择题
C,D,C,B,A,B,A,C,D,C,C,C.
二:填空题
13. 14. ±
15. 16.
三.解答题
17.(1)原式= (2)原式=-2tan
18.解 ∵sin α=-3cos α.
又sin2α+cos2α=1,得(-3cos α)2+cos2α=1,
即10cos2α=1.∴cos α=±.
又由sin α=-3cos α,可知sin α与cos α异号,
∴α在第二、四象限.
①当α是第二象限角时,sin α=,cos α=-.
②当α是第四象限角时,sin α=-,cos α=.
19.原式=
==
====-3.
20.解 (1)由图象易知函数f(x)的周期为
T=4×=2π,A=1,所以ω=1.
法一 由图可知此函数的图象是由y=sin x的图象向左平移个单位得到的,故φ=,所以函数解析式为f(x)=sin.
法二 由图象知f(x)过点.
则sin=0,
∴-+φ=kπ,k∈Z.
∴φ=kπ+,k∈Z,
又∵φ∈,
∴φ=,
∴f(x)=sin.
(2)方程f(x)=a在上有两个不同的 ( http: / / www.21cnjy.com )实根等价于y=f(x)与y=a的图象在上有两个交点,在图中作y=a的图象,如图为函数f(x)=sin在上的图象,当x=0时,f(x)=,当x=时,f(x)=0,由图中可以看出有两个交点时,a∈∪(-1,0).
( http: / / www.21cnjy.com )
21.解 (1)将x=0,y=代入函数y=2cos(ωx+θ)中,得cos θ=,因为0≤θ≤,所以θ=.
由已知T=π,且ω>0,得ω===2.
(2)因为点A,Q(x0,y0)是PA的中点,
y0=,所以点P的坐标为.
又因为点P在y=2cos的图象上,且≤x0≤π,
所以cos=,且≤4x0-≤,
从而得4x0-=,或4x0-=,即x0=,或x0=.
解 (1)图略
(2)T==π,由2kπ-≤2x+≤2kπ+,k∈Z知kπ-≤x≤kπ+(k∈Z).
所以所求的单调递增区间为(k∈Z).
(2)变换情况如下:y=sin 2x
y=sin
y=sin+1
同课章节目录
