九年级数学下册人教版第二十六章《反比例函数》单元测试题(含答案)
文档属性
| 名称 | 九年级数学下册人教版第二十六章《反比例函数》单元测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 947.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-22 19:23:00 | ||
图片预览


文档简介
九年级数学下册人教版第二十六章《反比例函数》单元测试题
一、单选题
1.如果 ,那么函数与 在同一平面直角坐标系中的图像可能是( )
A. B.
C. D.
2.已知正比例函数的图象与反比例函数的图象交于A,B两点,如果点的坐标是,那么点的坐标是( )
A. B. C. D.
3.如图,正比例函数与反比例函数的图象相交于A,B两点,轴于点C,则ΔABC的面积为( )
A.1 B.2 C. D.
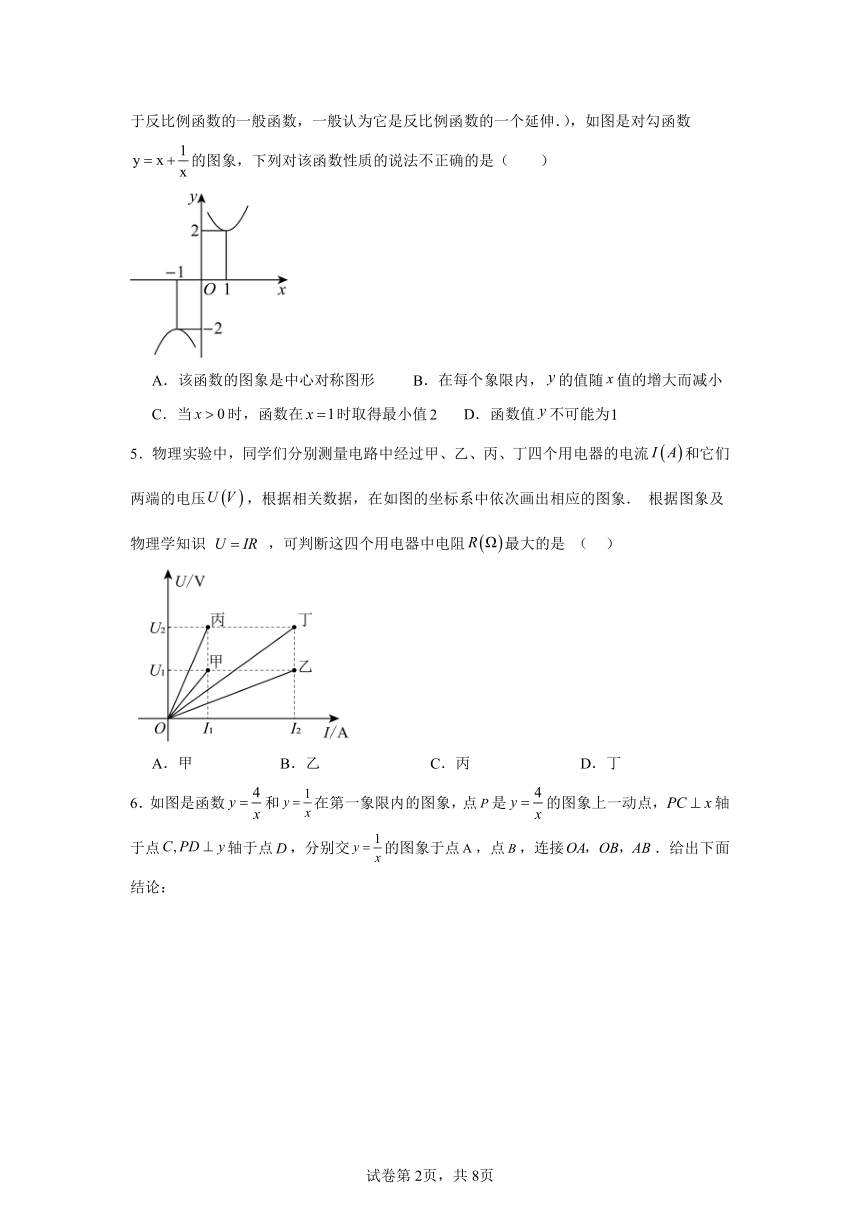
4.将正比例函数与反比例函数叠加得到函数(这样的函数由于其图象类似两个勾号,所以也称为“对勾函数”或“双勾函数”.对勾函数是一种类似于反比例函数的一般函数,一般认为它是反比例函数的一个延伸.),如图是对勾函数的图象,下列对该函数性质的说法不正确的是( )
A.该函数的图象是中心对称图形 B.在每个象限内,的值随值的增大而减小
C.当时,函数在时取得最小值 D.函数值不可能为
5.物理实验中,同学们分别测量电路中经过甲、乙、丙、丁四个用电器的电流和它们两端的电压,根据相关数据,在如图的坐标系中依次画出相应的图象. 根据图象及物理学知识 ,可判断这四个用电器中电阻最大的是 ( )
A.甲 B.乙 C.丙 D.丁
6.如图是函数和在第一象限内的图象,点是的图象上一动点,轴于点轴于点,分别交的图象于点,点,连接.给出下面结论:
①与的面积相等;②与始终相等;③ΔAOB的面积大小不会发生变化;④.其中正确结论的序号是()
A.①②③ B.②③④ C.①②④ D.①③④
7.如图,,是函数图象上两点,过点作轴的平行线,过点作轴的平行线,两直线交于点,若,则( )
A. B. C. D.
8.如图,等腰直角三角形的顶点A在反比例函数的图象上,顶点B,C在反比例函数的图象上,且轴.若点C的坐标为,则的值为 ( )
A. B. C. D.
二、填空题
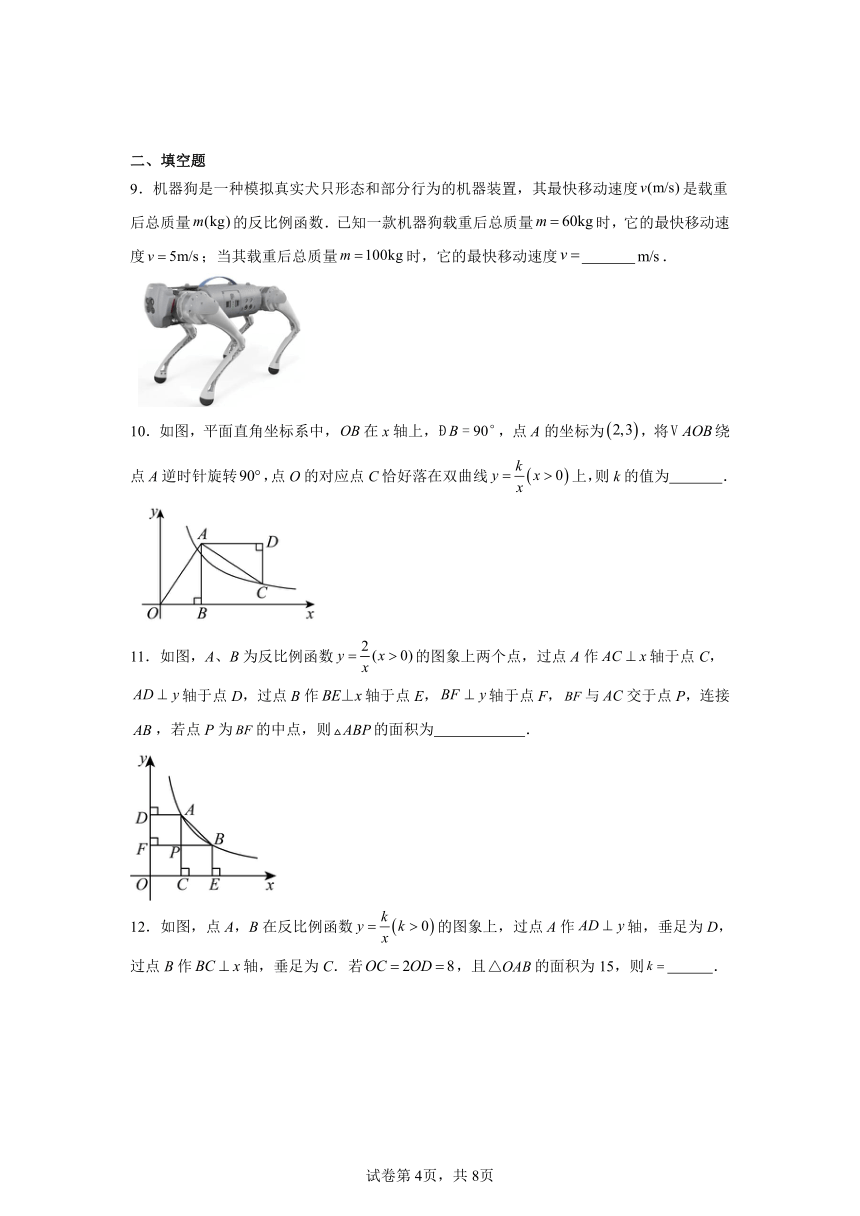
9.机器狗是一种模拟真实犬只形态和部分行为的机器装置,其最快移动速度是载重后总质量的反比例函数.已知一款机器狗载重后总质量时,它的最快移动速度;当其载重后总质量时,它的最快移动速度 .
10.如图,平面直角坐标系中,在x轴上,,点A的坐标为,将绕点A逆时针旋转,点O的对应点C恰好落在双曲线上,则k的值为 .
11.如图,A、B为反比例函数的图象上两个点,过点A作轴于点C,轴于点D,过点B作轴于点E,轴于点F,与交于点P,连接,若点P为的中点,则的面积为 .
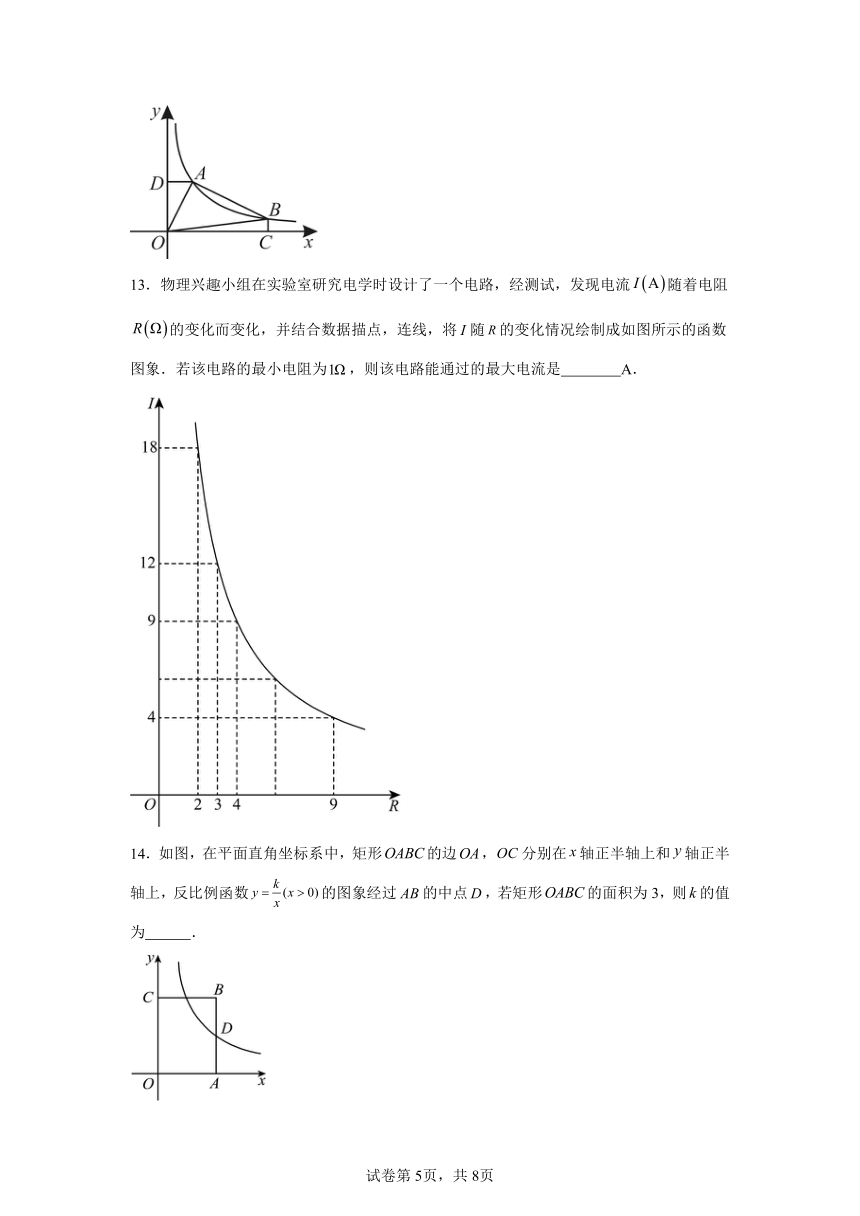
12.如图,点A,B在反比例函数的图象上,过点A作轴,垂足为D,过点B作轴,垂足为C.若,且的面积为15,则 .
13.物理兴趣小组在实验室研究电学时设计了一个电路,经测试,发现电流随着电阻的变化而变化,并结合数据描点,连线,将随的变化情况绘制成如图所示的函数图象.若该电路的最小电阻为,则该电路能通过的最大电流是 A.
14.如图,在平面直角坐标系中,矩形的边,分别在轴正半轴上和轴正半轴上,反比例函数的图象经过的中点,若矩形的面积为3,则的值为 .
三、解答题
15.如图,在平面直角坐标系中,O为坐标原点,点A、B在函数的图象上(点A的纵坐标大于点B的纵坐标),点A的坐标为,过点A作轴于点D,过点B作轴于点C,,连结、.
(1)求B点的坐标.
(2)求四边形的面积.
16.如图,在平面直角坐标系中,一次函数y=﹣2x的图象与反比例函数y=的图象交于点A(﹣1,n).
(1)求反比例函数y=的解析式;
(2)若P是x轴上一点,且△AOP是等腰三角形,求点P的坐标;
(3)结合图象直接写出不等式+2x>0的解集为 .
17.如图,一次函数与反比例函数的图象交于,两点.
(1)求这两个函数的解析式;
(2)根据图象,直接写出满足时,x的取值范围;
(3)点在线段上,过点P作x轴的垂线,垂足为M,交反比例函数的图象于点Q,求的面积.
18.如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于点、,与、轴分别交于点、.的顶点在第一象限内,且在的图象上,顶点在轴上.若点的坐标为,且.
(1)求一次函数解析式和反比例函数的解析式:
(2)将向下平移,当点落在这个反比例函数的图象上时,平移的距离为______;
(3)利用无刻度的直尺,在反比次函数的图象上作出点,使得(请用签字笔画图,不写作法,保留作图痕速).
19.如图,在平面直角坐标系中,反比例函数的图象与一次函数的图象交于点,.
(1)求一次函数的解析式,并在网格中画出一次函数的图象;
(2)结合图象,当时,直接写出自变量的取值范围;
(3)若点为轴上的一点,当的面积为时,求点的坐标.
20.如图,反比例函数()的图像经过点A,B,点A的坐标为,点B的纵坐标为3,点C的坐标为.
(1)如图①,求反比例函数和直线的函数表达式;
(2)如图②,P是直线上一点,D是x轴上一点,当的值最小时,求的最小值和此时点P的坐标;
(3)如图③,是反比例函数()图像上异于点A的一点,过点M作轴,垂足为N,过点A作轴,垂足为E,直线交x轴于点Q,是否存在点,使得四边形是菱形?若存在,请求出m的值;若不存在,请说明理由.
试卷第1页,共3页
试卷第1页,共3页
《九年级数学下册人教版第二十六章《反比例函数》单元测试题》参考答案
题号 1 2 3 4 5 6 7 8
答案 B A A B C D A B
9.3
10.
11./0.5
12.8
13.36
14.
15.(1)解:将点A的坐标代入可得,
的值为8;
函数的解析式为,
,,
,
,
点B的横坐标为6,将代入,得,
点B的坐标.
(2).
16.(1)利用待定系数法即可解决.
(2)分三种情形讨论①A为顶点,②O为顶点,③P为顶点,分别求解即可.
(3)先求出两个函数图象的交点坐标,然后根据图象,反比例函数图象在上面即可解决问题.
解:(1)∵点A(﹣1,n)在一次函数y=﹣2x上,
∴n=2,
∴点A坐标(﹣1,2)
把点A(﹣1,2)代入y=得k=﹣2,
∴反比例函数的解析式为y=﹣.
(2)①当A为等腰三角形顶点时,AO=AP,此时点P坐标为(﹣2,0).
②当点O为等腰三角形顶点时,OA=0P=,此时点P坐标为(﹣,0)或(,0)
③当点P为等腰三角形顶点时,OA的垂直平分线为:y=x+,y=0时,x=﹣,此时点P坐标(﹣,0).
(3)不等式+2x>0,即>﹣2x,
∵一次函数y=﹣2x的图象与反比例函数y=的图象交于点A(﹣1,2),B(1.2)
∴由图象可知﹣1<x<0或x>1.
故答案为﹣1<x<0或x>1.
17.(1)解:∵反比例函数的图象经过点,
,
,
∴反比例函数的解析式为;
把代入,得,
∴点坐标为,
∵一次函数解析式,经过,,
故得
解得,
∴一次函数解析式为;
(2)解:∵由,
∴,即反比例函数值小于一次函数值.
∴由函数图象可得,此时;
(3)解:在中,当时,,
在中,当时,,
∴
∴,
∴.
18.(1)解:把代入,得:,
∴,
∴,
当时,,
∴,
∴,
∵,
∴,
∵,
∴,
∵均在轴上,
∴轴,
∴,
∵点在反比例函数的图象上,
∴,
∴;
(2)∵,,
∴,
设平移距离为,则:平移后的坐标为:,
当平移后点在反比例函数图象上时,则:,
∴,
∴平移的距离为3;
(3)如图:点即为所求;
19.(1)把点代入,可得:
∴反比例函数的解析式为;
把点代入,可得,
把代入,得:
,
解得,
∴一次函数解析式为
画出函数图象如下:
(2)由图象得,当时,或
(3)∵一次函数解析式为
令,则,
∴一次函数与的交点坐标为,
∵的面积为,
∴
解得,或3
∴或
20.(1)解:∵反比例函数()的图像经过点,
∴,即,
∴;
∵点B的纵坐标为3,且在反比例函数的图像上,
∴,即,
∴;
设直线的函数表达式为,把B、C两点坐标分别代入其中,
得:,解得:,
∴.
即直线的函数表达式为.
(2)解:如图,作点A关于x轴的对称点E,连接,
则,,
∴,
则当三点共线,且时,的值最小;
设点,由勾股定理得,
∵,
∴,
当时,有最小值18,则有最小值;
当时,,即,
∴的最小值为,此时;
(3)解:存在,理由如下;
∵点M在反比例函数的图像上,且,
∴;
设直线解析式为,则有,解得:,
∴直线解析式为;
同理求得直线的解析式为;
由两直线解析式的系数相等得,且,
∴四边形是平行四边形;
∵四边形是菱形,
∴,
而,
∴,
解得(舍去),
即的值为.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如果 ,那么函数与 在同一平面直角坐标系中的图像可能是( )
A. B.
C. D.
2.已知正比例函数的图象与反比例函数的图象交于A,B两点,如果点的坐标是,那么点的坐标是( )
A. B. C. D.
3.如图,正比例函数与反比例函数的图象相交于A,B两点,轴于点C,则ΔABC的面积为( )
A.1 B.2 C. D.
4.将正比例函数与反比例函数叠加得到函数(这样的函数由于其图象类似两个勾号,所以也称为“对勾函数”或“双勾函数”.对勾函数是一种类似于反比例函数的一般函数,一般认为它是反比例函数的一个延伸.),如图是对勾函数的图象,下列对该函数性质的说法不正确的是( )
A.该函数的图象是中心对称图形 B.在每个象限内,的值随值的增大而减小
C.当时,函数在时取得最小值 D.函数值不可能为
5.物理实验中,同学们分别测量电路中经过甲、乙、丙、丁四个用电器的电流和它们两端的电压,根据相关数据,在如图的坐标系中依次画出相应的图象. 根据图象及物理学知识 ,可判断这四个用电器中电阻最大的是 ( )
A.甲 B.乙 C.丙 D.丁
6.如图是函数和在第一象限内的图象,点是的图象上一动点,轴于点轴于点,分别交的图象于点,点,连接.给出下面结论:
①与的面积相等;②与始终相等;③ΔAOB的面积大小不会发生变化;④.其中正确结论的序号是()
A.①②③ B.②③④ C.①②④ D.①③④
7.如图,,是函数图象上两点,过点作轴的平行线,过点作轴的平行线,两直线交于点,若,则( )
A. B. C. D.
8.如图,等腰直角三角形的顶点A在反比例函数的图象上,顶点B,C在反比例函数的图象上,且轴.若点C的坐标为,则的值为 ( )
A. B. C. D.
二、填空题
9.机器狗是一种模拟真实犬只形态和部分行为的机器装置,其最快移动速度是载重后总质量的反比例函数.已知一款机器狗载重后总质量时,它的最快移动速度;当其载重后总质量时,它的最快移动速度 .
10.如图,平面直角坐标系中,在x轴上,,点A的坐标为,将绕点A逆时针旋转,点O的对应点C恰好落在双曲线上,则k的值为 .
11.如图,A、B为反比例函数的图象上两个点,过点A作轴于点C,轴于点D,过点B作轴于点E,轴于点F,与交于点P,连接,若点P为的中点,则的面积为 .
12.如图,点A,B在反比例函数的图象上,过点A作轴,垂足为D,过点B作轴,垂足为C.若,且的面积为15,则 .
13.物理兴趣小组在实验室研究电学时设计了一个电路,经测试,发现电流随着电阻的变化而变化,并结合数据描点,连线,将随的变化情况绘制成如图所示的函数图象.若该电路的最小电阻为,则该电路能通过的最大电流是 A.
14.如图,在平面直角坐标系中,矩形的边,分别在轴正半轴上和轴正半轴上,反比例函数的图象经过的中点,若矩形的面积为3,则的值为 .
三、解答题
15.如图,在平面直角坐标系中,O为坐标原点,点A、B在函数的图象上(点A的纵坐标大于点B的纵坐标),点A的坐标为,过点A作轴于点D,过点B作轴于点C,,连结、.
(1)求B点的坐标.
(2)求四边形的面积.
16.如图,在平面直角坐标系中,一次函数y=﹣2x的图象与反比例函数y=的图象交于点A(﹣1,n).
(1)求反比例函数y=的解析式;
(2)若P是x轴上一点,且△AOP是等腰三角形,求点P的坐标;
(3)结合图象直接写出不等式+2x>0的解集为 .
17.如图,一次函数与反比例函数的图象交于,两点.
(1)求这两个函数的解析式;
(2)根据图象,直接写出满足时,x的取值范围;
(3)点在线段上,过点P作x轴的垂线,垂足为M,交反比例函数的图象于点Q,求的面积.
18.如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于点、,与、轴分别交于点、.的顶点在第一象限内,且在的图象上,顶点在轴上.若点的坐标为,且.
(1)求一次函数解析式和反比例函数的解析式:
(2)将向下平移,当点落在这个反比例函数的图象上时,平移的距离为______;
(3)利用无刻度的直尺,在反比次函数的图象上作出点,使得(请用签字笔画图,不写作法,保留作图痕速).
19.如图,在平面直角坐标系中,反比例函数的图象与一次函数的图象交于点,.
(1)求一次函数的解析式,并在网格中画出一次函数的图象;
(2)结合图象,当时,直接写出自变量的取值范围;
(3)若点为轴上的一点,当的面积为时,求点的坐标.
20.如图,反比例函数()的图像经过点A,B,点A的坐标为,点B的纵坐标为3,点C的坐标为.
(1)如图①,求反比例函数和直线的函数表达式;
(2)如图②,P是直线上一点,D是x轴上一点,当的值最小时,求的最小值和此时点P的坐标;
(3)如图③,是反比例函数()图像上异于点A的一点,过点M作轴,垂足为N,过点A作轴,垂足为E,直线交x轴于点Q,是否存在点,使得四边形是菱形?若存在,请求出m的值;若不存在,请说明理由.
试卷第1页,共3页
试卷第1页,共3页
《九年级数学下册人教版第二十六章《反比例函数》单元测试题》参考答案
题号 1 2 3 4 5 6 7 8
答案 B A A B C D A B
9.3
10.
11./0.5
12.8
13.36
14.
15.(1)解:将点A的坐标代入可得,
的值为8;
函数的解析式为,
,,
,
,
点B的横坐标为6,将代入,得,
点B的坐标.
(2).
16.(1)利用待定系数法即可解决.
(2)分三种情形讨论①A为顶点,②O为顶点,③P为顶点,分别求解即可.
(3)先求出两个函数图象的交点坐标,然后根据图象,反比例函数图象在上面即可解决问题.
解:(1)∵点A(﹣1,n)在一次函数y=﹣2x上,
∴n=2,
∴点A坐标(﹣1,2)
把点A(﹣1,2)代入y=得k=﹣2,
∴反比例函数的解析式为y=﹣.
(2)①当A为等腰三角形顶点时,AO=AP,此时点P坐标为(﹣2,0).
②当点O为等腰三角形顶点时,OA=0P=,此时点P坐标为(﹣,0)或(,0)
③当点P为等腰三角形顶点时,OA的垂直平分线为:y=x+,y=0时,x=﹣,此时点P坐标(﹣,0).
(3)不等式+2x>0,即>﹣2x,
∵一次函数y=﹣2x的图象与反比例函数y=的图象交于点A(﹣1,2),B(1.2)
∴由图象可知﹣1<x<0或x>1.
故答案为﹣1<x<0或x>1.
17.(1)解:∵反比例函数的图象经过点,
,
,
∴反比例函数的解析式为;
把代入,得,
∴点坐标为,
∵一次函数解析式,经过,,
故得
解得,
∴一次函数解析式为;
(2)解:∵由,
∴,即反比例函数值小于一次函数值.
∴由函数图象可得,此时;
(3)解:在中,当时,,
在中,当时,,
∴
∴,
∴.
18.(1)解:把代入,得:,
∴,
∴,
当时,,
∴,
∴,
∵,
∴,
∵,
∴,
∵均在轴上,
∴轴,
∴,
∵点在反比例函数的图象上,
∴,
∴;
(2)∵,,
∴,
设平移距离为,则:平移后的坐标为:,
当平移后点在反比例函数图象上时,则:,
∴,
∴平移的距离为3;
(3)如图:点即为所求;
19.(1)把点代入,可得:
∴反比例函数的解析式为;
把点代入,可得,
把代入,得:
,
解得,
∴一次函数解析式为
画出函数图象如下:
(2)由图象得,当时,或
(3)∵一次函数解析式为
令,则,
∴一次函数与的交点坐标为,
∵的面积为,
∴
解得,或3
∴或
20.(1)解:∵反比例函数()的图像经过点,
∴,即,
∴;
∵点B的纵坐标为3,且在反比例函数的图像上,
∴,即,
∴;
设直线的函数表达式为,把B、C两点坐标分别代入其中,
得:,解得:,
∴.
即直线的函数表达式为.
(2)解:如图,作点A关于x轴的对称点E,连接,
则,,
∴,
则当三点共线,且时,的值最小;
设点,由勾股定理得,
∵,
∴,
当时,有最小值18,则有最小值;
当时,,即,
∴的最小值为,此时;
(3)解:存在,理由如下;
∵点M在反比例函数的图像上,且,
∴;
设直线解析式为,则有,解得:,
∴直线解析式为;
同理求得直线的解析式为;
由两直线解析式的系数相等得,且,
∴四边形是平行四边形;
∵四边形是菱形,
∴,
而,
∴,
解得(舍去),
即的值为.
答案第1页,共2页
答案第1页,共2页
