江西省景德镇市乐平中学2024-2025学年高一下学期4月期中考试 数学试题(含答案)
文档属性
| 名称 | 江西省景德镇市乐平中学2024-2025学年高一下学期4月期中考试 数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 770.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-23 10:24:43 | ||
图片预览



文档简介
景德镇市2024-2025学年下学期期中质量检测卷
高一数学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.
第Ⅰ卷(选择题)
一、选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若且,则的终边在所在象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.抛一枚质地均匀的硬币100次,58次出现正面朝上,若再抛一次,则仍然是正面朝上的概率为( )
A. B. C. D.
3.角的终边与的终边关于轴对称,则( )
A. B.
C. D.
4.《九章算术》中有“米谷粒分”题:粮仓开仓收粮,有人送米1805石(古代容量单位),验得米内夹谷,抽样取米一把,数得155粒内夹谷31粒,则这批米内夹谷约为( )
A.361石 B.341石 C.314石 D.360石
5.抛一枚质地均匀的骰子两次,设事件表示“第二次朝上的数字为偶数”,则下列事件中与事件相互独立的是( )
A.第二次朝上的数字是奇数 B.第二次朝上的数字为2
C.两次朝上的数字之和为9 D.两次朝上的数字之和为10
6.已知,且,则( )
A. B. C. D.
7.已知函数,在内至少出现3次最大值,则的最小值为( )
A. B. C. D.3
8.如图所示,有一圆形图案,小红准备在扇形环面区域(由扇形去掉扇形构成)涂上颜色,已知厘米,厘米,扇形环面区域面积为100平方厘米,圆心角为弧度.记扇环的周长为厘米,的最小值为( )
A.最小值为20厘米 B.最小值为40厘米
C.最小值为60厘米 D.最小值为80厘米
二、选择题:本题共3小题,每小题6分,共18分,在每小题给出的四个选项中,有多项符合题目要求全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.下列说法正确的是( )
A.终边在轴上的角的集合为
B.是函数的图象的一个对称中心
C.把分针拨快15分钟,则分针旋转形成的角度为
D.
10.已知在一次随机试验中,定义两个随机事件和,若,,则( )
A.
B.
C.
D.若、相互独立,则和至少有一个发生的概率为
11.已知函数,为的零点,为图象的对称轴,且在区间上单调,下列结论正确的是( )
A.,其中
B.
C.当函数在区间上单调递增时,则
D.的最大值为7
第Ⅱ卷(非选择题)
三、填空题:本大题共3小题,每小题5分,共15分.
12.口袋中装有一些白球、黑球和红球,其中它们除颜色外完全相同,从中摸出1个球,摸出白球的概率为0.4,摸出黑球的概率为0.3,则摸出红球的概率为______.
13.函数的定义域是______.
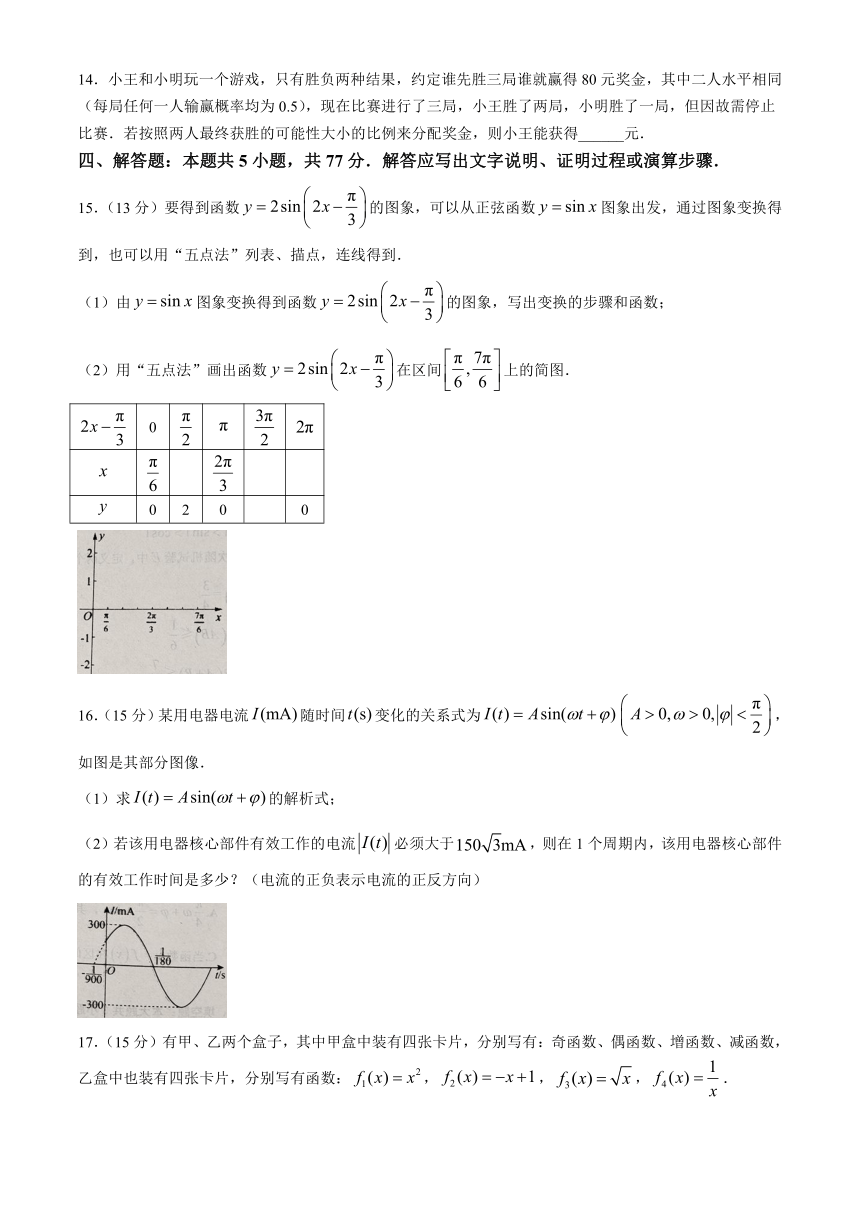
14.小王和小明玩一个游戏,只有胜负两种结果,约定谁先胜三局谁就赢得80元奖金,其中二人水平相同(每局任何一人输赢概率均为0.5),现在比赛进行了三局,小王胜了两局,小明胜了一局,但因故需停止比赛.若按照两人最终获胜的可能性大小的比例来分配奖金,则小王能获得______元.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)要得到函数的图象,可以从正弦函数图象出发,通过图象变换得到,也可以用“五点法”列表、描点,连线得到.
(1)由图象变换得到函数的图象,写出变换的步骤和函数;
(2)用“五点法”画出函数在区间上的简图.
0
0 2 0 0
16.(15分)某用电器电流随时间变化的关系式为,如图是其部分图像.
(1)求的解析式;
(2)若该用电器核心部件有效工作的电流必须大于,则在1个周期内,该用电器核心部件的有效工作时间是多少?(电流的正负表示电流的正反方向)
17.(15分)有甲、乙两个盒子,其中甲盒中装有四张卡片,分别写有:奇函数、偶函数、增函数、减函数,乙盒中也装有四张卡片,分别写有函数:,,,.
(1)若从乙盒中任取两张卡片,求这两张卡片上的函数的定义域不同的概率;
(2)若从甲、乙两盒中各取一张卡片,乙盒中的卡片上的函数恰好具备甲盒中的卡片上的函数的性质时,则称为一个“奇遇”,现从两盒中各取一张卡片,求它们恰好“奇遇”的概率.
18.(17分)在高一学生预选科之前,为了帮助他们更好地了解自己是否适合选读物理,某校从高一年级中随机抽取了100名学生的物理成绩,整理得到如图所示的频率分布直方图.
(1)求的值.若根据这次成绩,学校建议成绩排名前的学生选报物理,成绩排名后的学生选报历史,某同学想选报物理,请问他的物理成绩应不低于多少分较为合适?(小数点后保留一位)
(2)现学校要选拔学生参加物理竞赛,需要再进行考试.考试分为两轮,第一轮需要考2个模块,每个模块成绩从高到低依次有A+,A,B三个等级,若两个模块成绩均为A+,则直接参加;若一个模块成绩为A+,另一个模块成绩为A,则要参加第二轮实验操作,实验操作通过也能参加,否则均不能参加.现有甲、乙二人报名参加,二人互不影响,甲在每个模块考试中取得A+,A,B的概率分别为,,;乙在每个模块考试中取得A+,A,B的概率分别为,,;甲、乙在实验操作中通过的概率分别为,.求甲、乙至少有一个人能参加物理竞赛的概率.
19.(17分)已知函数,.
(1)求的对称轴方程,单调递增区间;
(2)若不等式对任意时恒成立,求实数应满足的条件;
(3)将函数的图象横坐标变为原来的,得到函数的图象,若存在非零常数,对任意,有成立,求满足条件的实数的集合.
景德镇市2024-2025学年度下学期期中质量检测
高一数学参考答案
第Ⅰ卷(选择题共58分)
一、选择题:本大题共8小题,每小题5分,满分40分.
1 2 3 4 5 6 7 8
C D D A C A B B
二、选择题:本大题共3小题,每小题6分,满分18分.
9 10 11
BD ACD AD
第Ⅱ卷(非选择题共92分)
三、填空题:本大题共3小题,每小题5分,满分15分.
12.0.3 13. 14.60
四、解答题:本大题共5小题,满分77分.
15.(本小题13分)解:(1)步骤1:把图象上所有点向右平移个单位长度,
得到函数的图象;
步骤2:把图象上所有点的横坐标变为原来的倍(纵坐标不变),
得到函数的图象;
步骤3:最后把函数的图象的纵坐标变为原来的2倍(横坐标不变),
得到函数的图象
(2)列表:
0
x
y 0 2 0 -2 0
16.(本小题15分)【解析】(1)∵周期,
∴,
又,∴,
将点代入上式,得,又,
∴,,
∴
(2)当时,此时,
令,
则或,
所以或,
解得或,
由,
得在1个周期内,该用电器核心部件的有效工作时间是
17.(本小题15分)【解析】(1)乙盒中的4个函数
,,,分别记为,
从乙盒中任取两张卡片,所有的取法为,共种,
又函数,的定义域均为,函数的定义域为,函数的定义域为,
所取函数的定义域不同的取法有,共5种,
所以这两张卡片上的函数的定义域不同的概率为.
(2)把甲盒中的奇函数、偶函数、增函数、减函数分别记为奇、偶、增、减,
则从甲、乙两盒中各取一张卡片有(奇,1),(奇,2),(奇,3),(奇,4),(偶,1),(偶,2),(偶,3),(偶,4),(增,1),(增,2),(增,3),(增,4),(减,1),(减,2),(减,3),(减,4),
共16种取法.
又是偶函数,是奇函数,是减函数,是增函数,恰为“奇遇”的有(偶,1),(奇4),(减,2),(增,3),共4种,
所以“奇遇”的概率为.
18.(本小题17分)【解析】(1)依题意得,,
又,
所以第分位数位于,且,
他的物理成绩应不低于分较为合适.
(2)依题意甲能参加物理竞赛的概率,
乙能参加物理竞赛的概率,
二人互不影响,所以甲、乙能同时参加物理竞赛的概率
19.(本小题17分)【解析】(1)对称轴方程为
单调递增区间为:
(2)
令,
∴,,
,
令,
∴,
解得:;
(3)∵横坐标变为原来的,
可得
∵,存在非零常数,对任意的,
成立,在上的值域为,在上的值域为
∴
当时,,所以,
即(且)
当时,
由诱导公式可得,
即,
所以当时,;
当时,
高一数学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.
第Ⅰ卷(选择题)
一、选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若且,则的终边在所在象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.抛一枚质地均匀的硬币100次,58次出现正面朝上,若再抛一次,则仍然是正面朝上的概率为( )
A. B. C. D.
3.角的终边与的终边关于轴对称,则( )
A. B.
C. D.
4.《九章算术》中有“米谷粒分”题:粮仓开仓收粮,有人送米1805石(古代容量单位),验得米内夹谷,抽样取米一把,数得155粒内夹谷31粒,则这批米内夹谷约为( )
A.361石 B.341石 C.314石 D.360石
5.抛一枚质地均匀的骰子两次,设事件表示“第二次朝上的数字为偶数”,则下列事件中与事件相互独立的是( )
A.第二次朝上的数字是奇数 B.第二次朝上的数字为2
C.两次朝上的数字之和为9 D.两次朝上的数字之和为10
6.已知,且,则( )
A. B. C. D.
7.已知函数,在内至少出现3次最大值,则的最小值为( )
A. B. C. D.3
8.如图所示,有一圆形图案,小红准备在扇形环面区域(由扇形去掉扇形构成)涂上颜色,已知厘米,厘米,扇形环面区域面积为100平方厘米,圆心角为弧度.记扇环的周长为厘米,的最小值为( )
A.最小值为20厘米 B.最小值为40厘米
C.最小值为60厘米 D.最小值为80厘米
二、选择题:本题共3小题,每小题6分,共18分,在每小题给出的四个选项中,有多项符合题目要求全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.下列说法正确的是( )
A.终边在轴上的角的集合为
B.是函数的图象的一个对称中心
C.把分针拨快15分钟,则分针旋转形成的角度为
D.
10.已知在一次随机试验中,定义两个随机事件和,若,,则( )
A.
B.
C.
D.若、相互独立,则和至少有一个发生的概率为
11.已知函数,为的零点,为图象的对称轴,且在区间上单调,下列结论正确的是( )
A.,其中
B.
C.当函数在区间上单调递增时,则
D.的最大值为7
第Ⅱ卷(非选择题)
三、填空题:本大题共3小题,每小题5分,共15分.
12.口袋中装有一些白球、黑球和红球,其中它们除颜色外完全相同,从中摸出1个球,摸出白球的概率为0.4,摸出黑球的概率为0.3,则摸出红球的概率为______.
13.函数的定义域是______.
14.小王和小明玩一个游戏,只有胜负两种结果,约定谁先胜三局谁就赢得80元奖金,其中二人水平相同(每局任何一人输赢概率均为0.5),现在比赛进行了三局,小王胜了两局,小明胜了一局,但因故需停止比赛.若按照两人最终获胜的可能性大小的比例来分配奖金,则小王能获得______元.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)要得到函数的图象,可以从正弦函数图象出发,通过图象变换得到,也可以用“五点法”列表、描点,连线得到.
(1)由图象变换得到函数的图象,写出变换的步骤和函数;
(2)用“五点法”画出函数在区间上的简图.
0
0 2 0 0
16.(15分)某用电器电流随时间变化的关系式为,如图是其部分图像.
(1)求的解析式;
(2)若该用电器核心部件有效工作的电流必须大于,则在1个周期内,该用电器核心部件的有效工作时间是多少?(电流的正负表示电流的正反方向)
17.(15分)有甲、乙两个盒子,其中甲盒中装有四张卡片,分别写有:奇函数、偶函数、增函数、减函数,乙盒中也装有四张卡片,分别写有函数:,,,.
(1)若从乙盒中任取两张卡片,求这两张卡片上的函数的定义域不同的概率;
(2)若从甲、乙两盒中各取一张卡片,乙盒中的卡片上的函数恰好具备甲盒中的卡片上的函数的性质时,则称为一个“奇遇”,现从两盒中各取一张卡片,求它们恰好“奇遇”的概率.
18.(17分)在高一学生预选科之前,为了帮助他们更好地了解自己是否适合选读物理,某校从高一年级中随机抽取了100名学生的物理成绩,整理得到如图所示的频率分布直方图.
(1)求的值.若根据这次成绩,学校建议成绩排名前的学生选报物理,成绩排名后的学生选报历史,某同学想选报物理,请问他的物理成绩应不低于多少分较为合适?(小数点后保留一位)
(2)现学校要选拔学生参加物理竞赛,需要再进行考试.考试分为两轮,第一轮需要考2个模块,每个模块成绩从高到低依次有A+,A,B三个等级,若两个模块成绩均为A+,则直接参加;若一个模块成绩为A+,另一个模块成绩为A,则要参加第二轮实验操作,实验操作通过也能参加,否则均不能参加.现有甲、乙二人报名参加,二人互不影响,甲在每个模块考试中取得A+,A,B的概率分别为,,;乙在每个模块考试中取得A+,A,B的概率分别为,,;甲、乙在实验操作中通过的概率分别为,.求甲、乙至少有一个人能参加物理竞赛的概率.
19.(17分)已知函数,.
(1)求的对称轴方程,单调递增区间;
(2)若不等式对任意时恒成立,求实数应满足的条件;
(3)将函数的图象横坐标变为原来的,得到函数的图象,若存在非零常数,对任意,有成立,求满足条件的实数的集合.
景德镇市2024-2025学年度下学期期中质量检测
高一数学参考答案
第Ⅰ卷(选择题共58分)
一、选择题:本大题共8小题,每小题5分,满分40分.
1 2 3 4 5 6 7 8
C D D A C A B B
二、选择题:本大题共3小题,每小题6分,满分18分.
9 10 11
BD ACD AD
第Ⅱ卷(非选择题共92分)
三、填空题:本大题共3小题,每小题5分,满分15分.
12.0.3 13. 14.60
四、解答题:本大题共5小题,满分77分.
15.(本小题13分)解:(1)步骤1:把图象上所有点向右平移个单位长度,
得到函数的图象;
步骤2:把图象上所有点的横坐标变为原来的倍(纵坐标不变),
得到函数的图象;
步骤3:最后把函数的图象的纵坐标变为原来的2倍(横坐标不变),
得到函数的图象
(2)列表:
0
x
y 0 2 0 -2 0
16.(本小题15分)【解析】(1)∵周期,
∴,
又,∴,
将点代入上式,得,又,
∴,,
∴
(2)当时,此时,
令,
则或,
所以或,
解得或,
由,
得在1个周期内,该用电器核心部件的有效工作时间是
17.(本小题15分)【解析】(1)乙盒中的4个函数
,,,分别记为,
从乙盒中任取两张卡片,所有的取法为,共种,
又函数,的定义域均为,函数的定义域为,函数的定义域为,
所取函数的定义域不同的取法有,共5种,
所以这两张卡片上的函数的定义域不同的概率为.
(2)把甲盒中的奇函数、偶函数、增函数、减函数分别记为奇、偶、增、减,
则从甲、乙两盒中各取一张卡片有(奇,1),(奇,2),(奇,3),(奇,4),(偶,1),(偶,2),(偶,3),(偶,4),(增,1),(增,2),(增,3),(增,4),(减,1),(减,2),(减,3),(减,4),
共16种取法.
又是偶函数,是奇函数,是减函数,是增函数,恰为“奇遇”的有(偶,1),(奇4),(减,2),(增,3),共4种,
所以“奇遇”的概率为.
18.(本小题17分)【解析】(1)依题意得,,
又,
所以第分位数位于,且,
他的物理成绩应不低于分较为合适.
(2)依题意甲能参加物理竞赛的概率,
乙能参加物理竞赛的概率,
二人互不影响,所以甲、乙能同时参加物理竞赛的概率
19.(本小题17分)【解析】(1)对称轴方程为
单调递增区间为:
(2)
令,
∴,,
,
令,
∴,
解得:;
(3)∵横坐标变为原来的,
可得
∵,存在非零常数,对任意的,
成立,在上的值域为,在上的值域为
∴
当时,,所以,
即(且)
当时,
由诱导公式可得,
即,
所以当时,;
当时,
同课章节目录
