第九章图形的变换章节期中复习(含解析)
文档属性
| 名称 | 第九章图形的变换章节期中复习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 671.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-23 16:44:33 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第九章图形的变换章节期中复习苏科版2024—2025学年七年级下册
一、选择题
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.如图,△ABC绕点A逆时针旋转20°得到△AB′C′,点C恰好落在B′C′上,则∠ACB的度数为( )
A.60° B.70°
C.80° D.90°
3.如图,∠AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是6cm,则P1P2的长为( )
A.6cm B.5cm C.4cm D.3cm
4.小强站在镜前,从镜子中看到镜子对面墙上挂着的电子表,其读数如图所示,则电子表的实际时刻是( )
A.15:01 B.10:51 C.10:21 D.12:01
5.如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )
A.20cm B.22cm C.24cm D.26cm
6.如图,在△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为( )
A.13 B.17 C.18 D.21
二、填空题
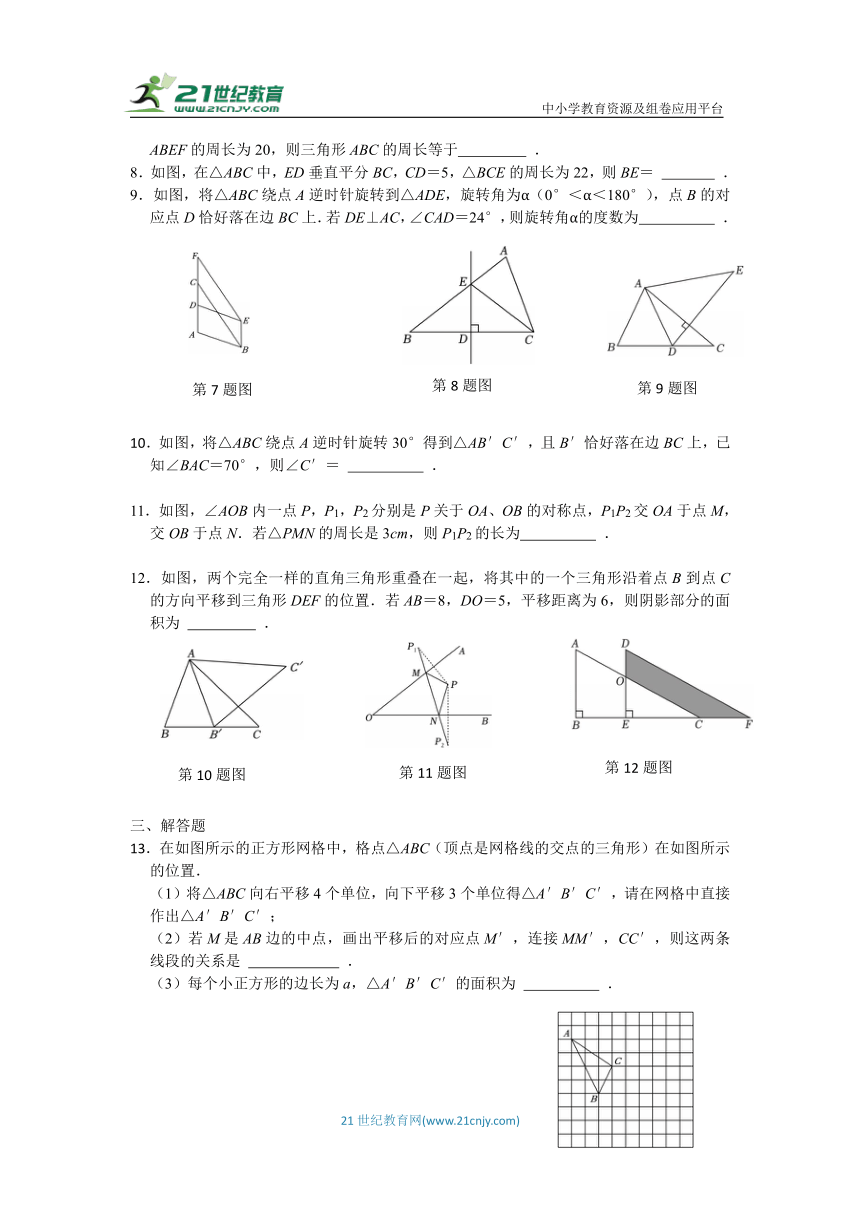
7.如图,三角形ABC沿AC边所在直线向上平移3个单位长度得到三角形DEF,四边形ABEF的周长为20,则三角形ABC的周长等于 .
8.如图,在△ABC中,ED垂直平分BC,CD=5,△BCE的周长为22,则BE= .
9.如图,将△ABC绕点A逆时针旋转到△ADE,旋转角为α(0°<α<180°),点B的对应点D恰好落在边BC上.若DE⊥AC,∠CAD=24°,则旋转角α的度数为 .
10.如图,将△ABC绕点A逆时针旋转30°得到△AB′C′,且B′恰好落在边BC上,已知∠BAC=70°,则∠C′= .
11.如图,∠AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是3cm,则P1P2的长为 .
12.如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着点B到点C的方向平移到三角形DEF的位置.若AB=8,DO=5,平移距离为6,则阴影部分的面积为 .
三、解答题
13.在如图所示的正方形网格中,格点△ABC(顶点是网格线的交点的三角形)在如图所示的位置.
(1)将△ABC向右平移4个单位,向下平移3个单位得△A′B′C′,请在网格中直接作出△A′B′C′;
(2)若M是AB边的中点,画出平移后的对应点M′,连接MM′,CC′,则这两条线段的关系是 .
(3)每个小正方形的边长为a,△A′B′C′的面积为 .
14.如图,△ABC中,∠ABC=30°,∠ACB=50°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.
(1)求∠DAF的度数;
(2)若△DAF的周长为20,求BC的长.
15.如图,已知在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接OB,OC,若△ADE的周长为8cm,△OBC的周长为18cm.
(1)求线段BC的长;
(2)连接OA,求线段OA的长;
(3)若∠BAC=120°,求∠DAE的度数.
16.国庆期间,广场上设置了一个庆祝国庆75周年的造型(如图所示).造型平面呈轴对称,其正中间为一个半径为a的半圆,摆放花草,其余部分为展板(阴影部分).(单位:米)
(1)摆放花草的面积为 米2,(用含a的代数式表示,结果保留π)展板的面积是 米2;(用含a的代数式表示)
(2)已知摆放花草部分造价为450元/平方米,展板部分造价为80元/平方米,当a=2时,求制作整个造型的造价(π取3).
17.如图,△ABC中,AB=BC,点O是△ABC内一点,将△ABO旋转后能与△BCD重合
(1)旋转中心是点 ;
(2)若∠ACB=70°,旋转角是 度;
(3)若∠ACB=60°,请判断△BOD的形状并说明理由.
18.如图,将长方形纸片ABCD沿MN和PQ折叠得到一个轴对称的帽子,折痕角∠AMN=∠DPQ,点A,D的对应点分别为点G,H,折叠后点B,C的对应点恰好都在点E.
(1)若折痕角∠AMN=110°,求帽子顶角∠NEQ的度数.
(2)设∠GMD=x度,∠NEQ=y度.
①请用含x的代数式表示y,则y= .
②当∠MNE=2∠GMD时,帽子比较美观,求此时y的值.
19.如图所示,已知O是∠APB内的一点,点M、N分别是O点关于PA、PB的对称点,MN与PA、PB分别相交于点E、F,已知MN=5cm.
(1)求△OEF的周长;
(2)若∠APB=α,求∠MPN(用含a的代数式表示).
参考答案
一、选择题
1.【解答】解:A、是轴对称图形,不是中心对称图形,不符合题意;
B、不是轴对称图形,是中心对称图形,不符合题意;
C、不是轴对称图形,是中心对称图形,不符合题意;
D、既是轴对称图形,又是中心对称图形,符合题意;
故选:D.
2.【解答】解:∵△ABC绕点A逆时针旋转20°得到△AB′C′,
∴∠CAC'=20°,AC=AC',∠ACB=∠C',
∴∠ACB=∠C'80°,
故选:C.
3.【解答】解:∵点P关于OA的对称点是P1,
∴P1M=PM.
∵点P关于OB的对称点是P2,
∴PN=P2N.
∵△PMN的周长=6cm,P1M=PM,PN=P2N,
∴P1P2=P1M+MN+P2N=PM+PN+MN=6cm,
故选:A.
4.【解答】解:电子表的实际时刻是10:21.
故选:C.
5.【解答】解:∵△ABC沿BC方向平移3cm得到△DEF,
∴DF=AC,AD=CF=3cm,
∵△ABC的周长为20cm,即AB+BC+AC=20cm,
∴AB+BC+CF+DF+AD=AB+BC+AC+AD+CF=20+3+3=26(cm),
即四边形ABFD的周长为26cm.
故选:D.
6.【解答】解:∵AB的垂直平分线DE交AB于点D,交边AC于点E,AC=8,BC=5,
∴AE=BE,
∴C△BCE=BE+CE+BC=AE+CE+BC=AC+BC=8+5=13.
故选:A.
二、填空题
7.【解答】解:∵△ABC沿AC边所在直线向上平移3个单位长度得到△DEF,
∴AD=BE=CF=3,BC=EF,
∵四边形ABEF的周长为20,
又∵四边形ABEF的周长=AB+BE+EF+AF=AB+AD+BC+AC+CF=20.
∴AB+3+BC+AC+3=20,
AB+BC+AC=14,
∴△ABC的周长为14.
故答案为:14.
8.【解答】解:由条件可知BC=2CD=10,CE=BE,
∵△BCE的周长为22,
∴BC+BE+CE=BC+2BE=22,即10+2BE=22,
∴BE=6,
故答案为:6.
9.【解答】解:如图,
∵DE⊥AC,
∴∠AFD=90°,
∵∠CAD=24°,
∴∠ADE=180°﹣∠CAD﹣∠AFD=180°﹣24°﹣90°=66°,
∵旋转,
∴∠B=∠ADE=66°,AB=AD,
∴∠ADB=∠B=66°,
∴∠BAD=180°﹣∠B﹣∠ABD=180°﹣66°﹣66°=48°,
即旋转角α的度数是48°.
故答案为:48°.
10.【解答】解:∵将△ABC绕点A逆时针旋转30°得到△AB′C′,且B′恰好落在边BC上,
∴∠BAB'=30°,AB=AB',∠C=∠C',
∴∠ABB'=∠AB'B=(180°﹣30°)÷2=75°,
∵∠BAC=70°,
∴∠B'AC=∠BAC﹣∠BAB'=70°﹣30°=40°,
∴∠C=∠AB'B﹣∠B'AC=75°﹣40°=35°,
∴∠C'=35°.
故答案为:35°.
11.【解答】解:∵P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N,
∴MP=MP1,NP=NP2,
∵△PMN的周长是3cm,
∴MP+MN+NP=3cm,
∴P1P2=MP1+MN+NP2=MP+MN+NP=3cm.
故答案为:3cm.
12.【解答】解:由平移的性质知,BE=6,DE=AB=8,
∴OE=DE﹣DO=8﹣5=3,
由平移可知,S△ABC=S△DEF,
∴S四边形ODFC=S梯形ABEO(AB+OE) BE(8+3)×6=33.
故答案为:33.
三、解答题
13.解:(1)如图,△A′B′C′即为所求.
(2)由题意得,这两条线段的关系是平行且相等.
故答案为:平行且相等.
(3)△A′B′C′的面积为(2a+4a)×3aa×2a2a×4a=4a2.
故答案为:4a2.
14.【解答】解:(1)∵∠ABC+∠ACB+∠BAC=180°,
∴∠BAC=180°﹣30°﹣50°=100°;
∵DE是线段AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠ABC=30°,
同理可得,∠FAC=∠ACB=50°,
∴∠DAF=∠BAC﹣∠DAB﹣∠FAC=100°﹣30°﹣50°=20°;
(2)∵△DAF的周长为20,
∴DA+DF+FA=20,
由(1)可知,DA=DB,FA=FC,
∴BC=DB+DF+FC=DA+DF+FA=20.
15.【解答】解:(1)∵l1是AB边的垂直平分线,
∴DA=DB,
∵l2是AC边的垂直平分线,
∴EA=EC,
BC=BD+DE+EC=DA+DE+EA=8(cm);
(2)∵l1是AB边的垂直平分线,
∴OA=OB,
∵l2是AC边的垂直平分线,
∴OA=OC,
∵OB+OC+BC=18cm,
∴OA=OB=OC=5(cm);
(3)∵∠BAC=120°,
∴∠ABC+∠ACB=60°,
∵DA=DB,EA=EC,
∴∠BAD=∠ABC,∠EAC=∠ACB,
∴∠DAE=∠BAC﹣∠BAD﹣∠EAC=60°.
16.【解答】解:(1)摆放花草的面积为米2,展板的面积是8a米2;
故答案为:,8a;
(2)造价为:3980(元).
答:制作整个造型的造价为3980元.
17.【解答】解:(1)旋转中心是点B,
故答案为:B;
(2)∵AB=BC,
∴∠BAC=∠ACB=70°,
∴∠ABC=180°﹣∠BAC﹣∠ACB=40°,
∵将△ABO旋转后能与△BCD重合,
∴∠ABO=∠CBD,
∴∠OBC+∠ABO=∠OBC+∠CBD=∠ABC=40°,
∵旋转角是40度,
故答案为:40;
(3)△BOD是等边三角形,
∵AB=BC,∠ACB=60°,
∴△ABC是等边三角形,
∴∠ABC=60°,
∵将△ABO旋转后能与△BCD重合,
∴BD=BO,
∵∠OBD=∠ABC=60°,
∴△BOD是等边三角形.
18.【解答】解:(1)由题意可知AD∥BC,
∴∠AMN+∠MNB=180°,
又∵∠AMN=110°,
∴∠MNB=70°,
由折叠的性质得:∠MNB=∠MNE=70°,
∴∠ENQ=180°﹣70°﹣70°=40°,
由折痕角∠AMN=∠DPQ可知:EN=EQ,
在△NEQ中,∠NEQ=180°﹣40°﹣40°=100°;
(2)①由题意可知AD∥BC,MG∥NE,
∴∠DMN+∠MNE+∠ENQ=180°,∠GMD+∠DMN+∠MNE=180°,
∴∠GMD=∠ENQ,
设∠GMD=x度,∠NEQ=y度,则∠ENQ=x度,
在△NEQ中,2x+y=180°,
∴y=180°﹣2x,
故答案为:y=180°﹣2x;
②由①知,∠GMD=∠ENQ,
∵∠MNE=2∠GMD,∠MNE=∠MNB,
由∠MNB+∠MNE+∠ENQ=180°,
∴2∠GMD+2∠GMD+∠GMD=180°,
∴∠GMD=36°,
即x=36°,
由①知,y=180°﹣2x
∴y=180°﹣2×36°=108°.
19.【解答】解:(1)∵M,N分别是点O关于PA、PB的对称点,
∴EM=EO,FN=FO,
∴△OEF的周长=OE+OF+EF
=ME+EF+FN=MN
=5(cm);
(2)如图,连接PM,PN,PO,
∵M,N分别是点O关于PA、PB的对称点,
∴∠MPA=∠OPA,∠NPB=∠OPB,
∴∠MPN=2∠APB=2α.
21世纪教育网(www.21cnjy.com)
第九章图形的变换章节期中复习苏科版2024—2025学年七年级下册
一、选择题
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.如图,△ABC绕点A逆时针旋转20°得到△AB′C′,点C恰好落在B′C′上,则∠ACB的度数为( )
A.60° B.70°
C.80° D.90°
3.如图,∠AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是6cm,则P1P2的长为( )
A.6cm B.5cm C.4cm D.3cm
4.小强站在镜前,从镜子中看到镜子对面墙上挂着的电子表,其读数如图所示,则电子表的实际时刻是( )
A.15:01 B.10:51 C.10:21 D.12:01
5.如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )
A.20cm B.22cm C.24cm D.26cm
6.如图,在△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为( )
A.13 B.17 C.18 D.21
二、填空题
7.如图,三角形ABC沿AC边所在直线向上平移3个单位长度得到三角形DEF,四边形ABEF的周长为20,则三角形ABC的周长等于 .
8.如图,在△ABC中,ED垂直平分BC,CD=5,△BCE的周长为22,则BE= .
9.如图,将△ABC绕点A逆时针旋转到△ADE,旋转角为α(0°<α<180°),点B的对应点D恰好落在边BC上.若DE⊥AC,∠CAD=24°,则旋转角α的度数为 .
10.如图,将△ABC绕点A逆时针旋转30°得到△AB′C′,且B′恰好落在边BC上,已知∠BAC=70°,则∠C′= .
11.如图,∠AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是3cm,则P1P2的长为 .
12.如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着点B到点C的方向平移到三角形DEF的位置.若AB=8,DO=5,平移距离为6,则阴影部分的面积为 .
三、解答题
13.在如图所示的正方形网格中,格点△ABC(顶点是网格线的交点的三角形)在如图所示的位置.
(1)将△ABC向右平移4个单位,向下平移3个单位得△A′B′C′,请在网格中直接作出△A′B′C′;
(2)若M是AB边的中点,画出平移后的对应点M′,连接MM′,CC′,则这两条线段的关系是 .
(3)每个小正方形的边长为a,△A′B′C′的面积为 .
14.如图,△ABC中,∠ABC=30°,∠ACB=50°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.
(1)求∠DAF的度数;
(2)若△DAF的周长为20,求BC的长.
15.如图,已知在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接OB,OC,若△ADE的周长为8cm,△OBC的周长为18cm.
(1)求线段BC的长;
(2)连接OA,求线段OA的长;
(3)若∠BAC=120°,求∠DAE的度数.
16.国庆期间,广场上设置了一个庆祝国庆75周年的造型(如图所示).造型平面呈轴对称,其正中间为一个半径为a的半圆,摆放花草,其余部分为展板(阴影部分).(单位:米)
(1)摆放花草的面积为 米2,(用含a的代数式表示,结果保留π)展板的面积是 米2;(用含a的代数式表示)
(2)已知摆放花草部分造价为450元/平方米,展板部分造价为80元/平方米,当a=2时,求制作整个造型的造价(π取3).
17.如图,△ABC中,AB=BC,点O是△ABC内一点,将△ABO旋转后能与△BCD重合
(1)旋转中心是点 ;
(2)若∠ACB=70°,旋转角是 度;
(3)若∠ACB=60°,请判断△BOD的形状并说明理由.
18.如图,将长方形纸片ABCD沿MN和PQ折叠得到一个轴对称的帽子,折痕角∠AMN=∠DPQ,点A,D的对应点分别为点G,H,折叠后点B,C的对应点恰好都在点E.
(1)若折痕角∠AMN=110°,求帽子顶角∠NEQ的度数.
(2)设∠GMD=x度,∠NEQ=y度.
①请用含x的代数式表示y,则y= .
②当∠MNE=2∠GMD时,帽子比较美观,求此时y的值.
19.如图所示,已知O是∠APB内的一点,点M、N分别是O点关于PA、PB的对称点,MN与PA、PB分别相交于点E、F,已知MN=5cm.
(1)求△OEF的周长;
(2)若∠APB=α,求∠MPN(用含a的代数式表示).
参考答案
一、选择题
1.【解答】解:A、是轴对称图形,不是中心对称图形,不符合题意;
B、不是轴对称图形,是中心对称图形,不符合题意;
C、不是轴对称图形,是中心对称图形,不符合题意;
D、既是轴对称图形,又是中心对称图形,符合题意;
故选:D.
2.【解答】解:∵△ABC绕点A逆时针旋转20°得到△AB′C′,
∴∠CAC'=20°,AC=AC',∠ACB=∠C',
∴∠ACB=∠C'80°,
故选:C.
3.【解答】解:∵点P关于OA的对称点是P1,
∴P1M=PM.
∵点P关于OB的对称点是P2,
∴PN=P2N.
∵△PMN的周长=6cm,P1M=PM,PN=P2N,
∴P1P2=P1M+MN+P2N=PM+PN+MN=6cm,
故选:A.
4.【解答】解:电子表的实际时刻是10:21.
故选:C.
5.【解答】解:∵△ABC沿BC方向平移3cm得到△DEF,
∴DF=AC,AD=CF=3cm,
∵△ABC的周长为20cm,即AB+BC+AC=20cm,
∴AB+BC+CF+DF+AD=AB+BC+AC+AD+CF=20+3+3=26(cm),
即四边形ABFD的周长为26cm.
故选:D.
6.【解答】解:∵AB的垂直平分线DE交AB于点D,交边AC于点E,AC=8,BC=5,
∴AE=BE,
∴C△BCE=BE+CE+BC=AE+CE+BC=AC+BC=8+5=13.
故选:A.
二、填空题
7.【解答】解:∵△ABC沿AC边所在直线向上平移3个单位长度得到△DEF,
∴AD=BE=CF=3,BC=EF,
∵四边形ABEF的周长为20,
又∵四边形ABEF的周长=AB+BE+EF+AF=AB+AD+BC+AC+CF=20.
∴AB+3+BC+AC+3=20,
AB+BC+AC=14,
∴△ABC的周长为14.
故答案为:14.
8.【解答】解:由条件可知BC=2CD=10,CE=BE,
∵△BCE的周长为22,
∴BC+BE+CE=BC+2BE=22,即10+2BE=22,
∴BE=6,
故答案为:6.
9.【解答】解:如图,
∵DE⊥AC,
∴∠AFD=90°,
∵∠CAD=24°,
∴∠ADE=180°﹣∠CAD﹣∠AFD=180°﹣24°﹣90°=66°,
∵旋转,
∴∠B=∠ADE=66°,AB=AD,
∴∠ADB=∠B=66°,
∴∠BAD=180°﹣∠B﹣∠ABD=180°﹣66°﹣66°=48°,
即旋转角α的度数是48°.
故答案为:48°.
10.【解答】解:∵将△ABC绕点A逆时针旋转30°得到△AB′C′,且B′恰好落在边BC上,
∴∠BAB'=30°,AB=AB',∠C=∠C',
∴∠ABB'=∠AB'B=(180°﹣30°)÷2=75°,
∵∠BAC=70°,
∴∠B'AC=∠BAC﹣∠BAB'=70°﹣30°=40°,
∴∠C=∠AB'B﹣∠B'AC=75°﹣40°=35°,
∴∠C'=35°.
故答案为:35°.
11.【解答】解:∵P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N,
∴MP=MP1,NP=NP2,
∵△PMN的周长是3cm,
∴MP+MN+NP=3cm,
∴P1P2=MP1+MN+NP2=MP+MN+NP=3cm.
故答案为:3cm.
12.【解答】解:由平移的性质知,BE=6,DE=AB=8,
∴OE=DE﹣DO=8﹣5=3,
由平移可知,S△ABC=S△DEF,
∴S四边形ODFC=S梯形ABEO(AB+OE) BE(8+3)×6=33.
故答案为:33.
三、解答题
13.解:(1)如图,△A′B′C′即为所求.
(2)由题意得,这两条线段的关系是平行且相等.
故答案为:平行且相等.
(3)△A′B′C′的面积为(2a+4a)×3aa×2a2a×4a=4a2.
故答案为:4a2.
14.【解答】解:(1)∵∠ABC+∠ACB+∠BAC=180°,
∴∠BAC=180°﹣30°﹣50°=100°;
∵DE是线段AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠ABC=30°,
同理可得,∠FAC=∠ACB=50°,
∴∠DAF=∠BAC﹣∠DAB﹣∠FAC=100°﹣30°﹣50°=20°;
(2)∵△DAF的周长为20,
∴DA+DF+FA=20,
由(1)可知,DA=DB,FA=FC,
∴BC=DB+DF+FC=DA+DF+FA=20.
15.【解答】解:(1)∵l1是AB边的垂直平分线,
∴DA=DB,
∵l2是AC边的垂直平分线,
∴EA=EC,
BC=BD+DE+EC=DA+DE+EA=8(cm);
(2)∵l1是AB边的垂直平分线,
∴OA=OB,
∵l2是AC边的垂直平分线,
∴OA=OC,
∵OB+OC+BC=18cm,
∴OA=OB=OC=5(cm);
(3)∵∠BAC=120°,
∴∠ABC+∠ACB=60°,
∵DA=DB,EA=EC,
∴∠BAD=∠ABC,∠EAC=∠ACB,
∴∠DAE=∠BAC﹣∠BAD﹣∠EAC=60°.
16.【解答】解:(1)摆放花草的面积为米2,展板的面积是8a米2;
故答案为:,8a;
(2)造价为:3980(元).
答:制作整个造型的造价为3980元.
17.【解答】解:(1)旋转中心是点B,
故答案为:B;
(2)∵AB=BC,
∴∠BAC=∠ACB=70°,
∴∠ABC=180°﹣∠BAC﹣∠ACB=40°,
∵将△ABO旋转后能与△BCD重合,
∴∠ABO=∠CBD,
∴∠OBC+∠ABO=∠OBC+∠CBD=∠ABC=40°,
∵旋转角是40度,
故答案为:40;
(3)△BOD是等边三角形,
∵AB=BC,∠ACB=60°,
∴△ABC是等边三角形,
∴∠ABC=60°,
∵将△ABO旋转后能与△BCD重合,
∴BD=BO,
∵∠OBD=∠ABC=60°,
∴△BOD是等边三角形.
18.【解答】解:(1)由题意可知AD∥BC,
∴∠AMN+∠MNB=180°,
又∵∠AMN=110°,
∴∠MNB=70°,
由折叠的性质得:∠MNB=∠MNE=70°,
∴∠ENQ=180°﹣70°﹣70°=40°,
由折痕角∠AMN=∠DPQ可知:EN=EQ,
在△NEQ中,∠NEQ=180°﹣40°﹣40°=100°;
(2)①由题意可知AD∥BC,MG∥NE,
∴∠DMN+∠MNE+∠ENQ=180°,∠GMD+∠DMN+∠MNE=180°,
∴∠GMD=∠ENQ,
设∠GMD=x度,∠NEQ=y度,则∠ENQ=x度,
在△NEQ中,2x+y=180°,
∴y=180°﹣2x,
故答案为:y=180°﹣2x;
②由①知,∠GMD=∠ENQ,
∵∠MNE=2∠GMD,∠MNE=∠MNB,
由∠MNB+∠MNE+∠ENQ=180°,
∴2∠GMD+2∠GMD+∠GMD=180°,
∴∠GMD=36°,
即x=36°,
由①知,y=180°﹣2x
∴y=180°﹣2×36°=108°.
19.【解答】解:(1)∵M,N分别是点O关于PA、PB的对称点,
∴EM=EO,FN=FO,
∴△OEF的周长=OE+OF+EF
=ME+EF+FN=MN
=5(cm);
(2)如图,连接PM,PN,PO,
∵M,N分别是点O关于PA、PB的对称点,
∴∠MPA=∠OPA,∠NPB=∠OPB,
∴∠MPN=2∠APB=2α.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
