上海市松江二中09-10学年高二上学期12月月考(数学)
文档属性
| 名称 | 上海市松江二中09-10学年高二上学期12月月考(数学) |  | |
| 格式 | rar | ||
| 文件大小 | 232.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-12-30 19:32:00 | ||
图片预览



文档简介
上海市松江二中2009学年度第一学期月考试题
高 二 数 学
编辑校对:刘彦利
一.填空题(每题3分,共33分):
1.设则 .
2.设是函数的反函数,则方程的解 .
3.向量满足与的夹角为,则.
4.在中,,是边的中点,则 .
5.设等差数列的前项和为,若,则 ______.
6.执行右边的程序框图,输出的T= .
7.已知二面角的大小为,
为异面直线,且则
所成角的大小为 _____ .
8.设若是与的等比
中项,则的最小值为 .
9.在四边形中,,
,则四边形
的面积是 .21世纪教育网
10.使得函数的最小值是非负数的整数值的集合为 21世纪教育网.
11.已知点其中,设表示外接圆的面积,则= .21世纪教育网
二.选择题(每题3分,共12分):21世纪教育网
12.若为两条不同的直线,为两个不同的平面,则以下命题正确的是…( )
A.若,,则; B.若,,则;
C.若,,则; D.若,,则.21世纪教育网
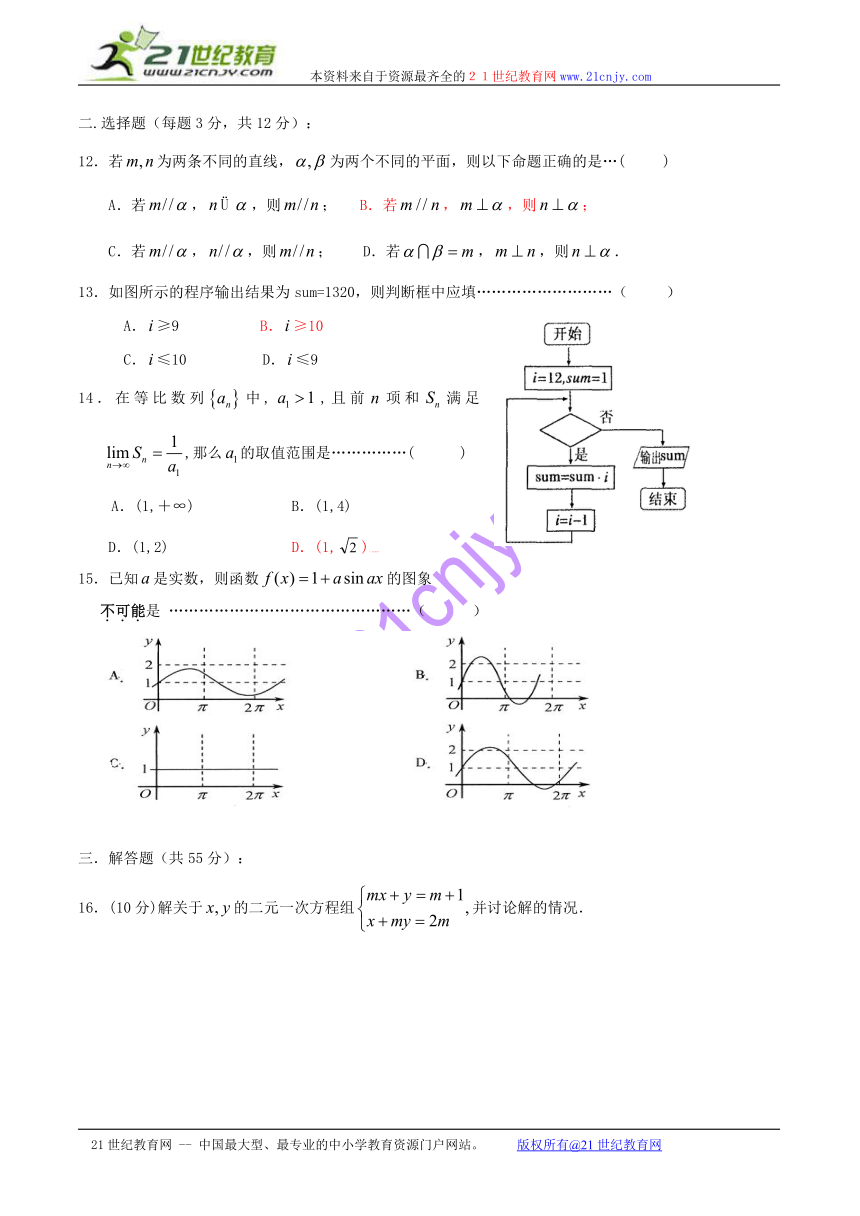
13.如图所示的程序输出结果为sum=1320,则判断框中应填………………………( )
A.≥9 B.≥10
C.≤10 D.≤921世纪教育网
14.在等比数列中,,且前项和满足 ,那么的取值范围是……………( )
A.(1,+∞) B.(1,4)
D.(1,2) D.(1,) 21世纪教育网
15.已知是实数,则函数的图象
不可能是 …………………………………………( )21世纪教育网
三.解答题(共55分):
16.(10分)解关于的二元一次方程组并讨论解的情况.21世纪教育网
17.(10分)如图,在棱长为2的正方体中,E是BC1的中点.求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示).21世纪教育网
18.(11分)已知向量.
(1)求向量的长度的最大值;21世纪教育网
(2)设,且,求的值.
19.(12分)已知数列的前项和为,,且().
(1)求数列的通项公式;21世纪教育网
(2)记,若对任意恒成立,求实数的最大值.
20.(12分)在直角坐标平面上的一列点简记为.若由构成的数列满足其中是与轴正方向同的单位向量),则称为点列.21世纪教育网
(1)判断是否为点列,并说明理由;
(2)若为点列,且点在点的右上方,任取其中连续三点判断的形状(锐角三角形、直角三角形、钝角三角形),并予以证明;
(3)若为点列,正整数满足求证:21世纪教育网
.
松江二中2009学年度高二月考数学试题答案
一.填空题(每题3分,共33分)
1.设则.【】21世纪教育网
2.函数是函数的反函数,则方程的解 .【】
3.向量满足与的夹角为,则.【】
4.在中,,是边的中点,则的值是 .【】
5.设等差数列的前n项和为,若,则 ______.【】21世纪教育网
6.执行右边的程序框图,输出的T= .【】
7. 已知二面角的大小为,为异面直线,且则 所成角的大小为 .【】
8.设若是与的等比中项,
则的最小值为 .【4】
9.在四边形中,,,则四边形的面积是 .【】21世纪教育网
10.若函数的最小值是非负数,则符合条件的整数值的集合为 .【】
11.已知点其中n的为正整数.设Sn表示△ABC外接圆的面积,则= .【4π】21世纪教育网
二.选择题(每题3分,共12分)
12.若、为两条不同的直线,、为两个不同的平面,则以下命题正确的是( B )
A.若,,则; B.若,,则;
C.若,,则; D.若,,则.
13.如图所示的程序输出结果为sum=1320,则判断框中应填( B )
A.≥9 B.≥10
C.≤10 D.≤9
14.在等比数列中,,且前项和满足 ,那么的取值范围是( D ) A. (1,+∞) B.(1,4)
C. (1,2) D.(1,)
15.已知是实数,则函数的图象不可能是( D )21世纪教育网
三.解答题:
16.(10分)解关于的二元一次方程组并讨论解的情况. 21世纪教育网
【解】 ……………………………?-……………………………2分………………………………4分
(1)当时,方程组有唯一解,…21世纪教育网…………………………………………6分
(2) 当时,方程组有无穷多组解,……………………………………8分
(3)当时,方程组无解. …………………………………………………………………10分
17.(10分)如图,在棱长为2的正方体中,E是BC1的中点.求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示).21世纪教育网
【解】过E作EF⊥BC,交BC于F,连接DF.
∵ EF⊥平面ABCD,
∴ ∠EDF是直线DE与平面ABCD所成的角. ……………4分
由题意,得EF=
∵ …………………………..6分
∵ EF⊥DF, ∴ ……………..8分
故直线DE与平面ABCD所成角的大小是….10分
18.(11分)已知向量
(Ⅰ)求向量的长度的最大值;21世纪教育网
(Ⅱ)设,且,求的值。
【解】(1)则……4分
,即 21世纪教育网
当时,有所以向量的长度的最大值为2.……………………5分
(2)解法1:由已知可得
。
,,即。……………………………………8分21世纪教育网
由,得,即。
,于是。………………………11分21世纪教育网
解法2:若,则,又由,得
,,即……………………………………8分21世纪教育网
,平方后化简得
解得或,经检验,即为所求……………………11分
19 .(12分)已知数列的前项和为,,且(为正整数).
(1)求数列的通项公式;21世纪教育网
(2)记.若对任意正整数,恒成立,求实数的最大值.
【解】(1), ①
当时,. ②
由 ① - ②,得.
……………………………………………………………………… 3分
又 ,,解得 .…………………………………………… 4分21世纪教育网
数列是首项为1,公比为的等比数列.
(为正整数). ………………………………………………… 6分21世纪教育网
(2)由(1)知,,. ……………… 8分21世纪教育网
由题意可知,对于任意的正整数,恒有,解得 .………10分
数列单调递增, 当时,数列中的最小项为,
必有,即实数的最大值为.…………………………………………………… 12分
20.(12分)在直角坐标平面上的一列点简记为.若由构成的数列满足其中为方向与轴正方向相同的单位向量,则称为点列. 21世纪教育网
(1)判断是否为点列,并说明理由;
(2)若为点列,且点在点的右上方.任取其中连续三点判断的形状(锐角三角形、直角三角形、钝角三角形),并予以证明;
(3)若为点列,正整数满足求证:21世纪教育网
【解】(1) , ,显然有,
是点列. ………………………………………………………………………… 3分
(2)在△中,,
.………………………………………… 5分
点在点的右上方,,
为点列,,
,则.
为钝角, △为钝角三角形.……………………………… 7分21世纪教育网
(3)[证明] ,. ①
. ②
同理. ③ ……………………………… 10分
由于为点列,于是,④
由①、②、③、④可推得
,,
即 . …………………………………………………………………… 12分21世纪教育网
高 二 数 学
编辑校对:刘彦利
一.填空题(每题3分,共33分):
1.设则 .
2.设是函数的反函数,则方程的解 .
3.向量满足与的夹角为,则.
4.在中,,是边的中点,则 .
5.设等差数列的前项和为,若,则 ______.
6.执行右边的程序框图,输出的T= .
7.已知二面角的大小为,
为异面直线,且则
所成角的大小为 _____ .
8.设若是与的等比
中项,则的最小值为 .
9.在四边形中,,
,则四边形
的面积是 .21世纪教育网
10.使得函数的最小值是非负数的整数值的集合为 21世纪教育网.
11.已知点其中,设表示外接圆的面积,则= .21世纪教育网
二.选择题(每题3分,共12分):21世纪教育网
12.若为两条不同的直线,为两个不同的平面,则以下命题正确的是…( )
A.若,,则; B.若,,则;
C.若,,则; D.若,,则.21世纪教育网
13.如图所示的程序输出结果为sum=1320,则判断框中应填………………………( )
A.≥9 B.≥10
C.≤10 D.≤921世纪教育网
14.在等比数列中,,且前项和满足 ,那么的取值范围是……………( )
A.(1,+∞) B.(1,4)
D.(1,2) D.(1,) 21世纪教育网
15.已知是实数,则函数的图象
不可能是 …………………………………………( )21世纪教育网
三.解答题(共55分):
16.(10分)解关于的二元一次方程组并讨论解的情况.21世纪教育网
17.(10分)如图,在棱长为2的正方体中,E是BC1的中点.求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示).21世纪教育网
18.(11分)已知向量.
(1)求向量的长度的最大值;21世纪教育网
(2)设,且,求的值.
19.(12分)已知数列的前项和为,,且().
(1)求数列的通项公式;21世纪教育网
(2)记,若对任意恒成立,求实数的最大值.
20.(12分)在直角坐标平面上的一列点简记为.若由构成的数列满足其中是与轴正方向同的单位向量),则称为点列.21世纪教育网
(1)判断是否为点列,并说明理由;
(2)若为点列,且点在点的右上方,任取其中连续三点判断的形状(锐角三角形、直角三角形、钝角三角形),并予以证明;
(3)若为点列,正整数满足求证:21世纪教育网
.
松江二中2009学年度高二月考数学试题答案
一.填空题(每题3分,共33分)
1.设则.【】21世纪教育网
2.函数是函数的反函数,则方程的解 .【】
3.向量满足与的夹角为,则.【】
4.在中,,是边的中点,则的值是 .【】
5.设等差数列的前n项和为,若,则 ______.【】21世纪教育网
6.执行右边的程序框图,输出的T= .【】
7. 已知二面角的大小为,为异面直线,且则 所成角的大小为 .【】
8.设若是与的等比中项,
则的最小值为 .【4】
9.在四边形中,,,则四边形的面积是 .【】21世纪教育网
10.若函数的最小值是非负数,则符合条件的整数值的集合为 .【】
11.已知点其中n的为正整数.设Sn表示△ABC外接圆的面积,则= .【4π】21世纪教育网
二.选择题(每题3分,共12分)
12.若、为两条不同的直线,、为两个不同的平面,则以下命题正确的是( B )
A.若,,则; B.若,,则;
C.若,,则; D.若,,则.
13.如图所示的程序输出结果为sum=1320,则判断框中应填( B )
A.≥9 B.≥10
C.≤10 D.≤9
14.在等比数列中,,且前项和满足 ,那么的取值范围是( D ) A. (1,+∞) B.(1,4)
C. (1,2) D.(1,)
15.已知是实数,则函数的图象不可能是( D )21世纪教育网
三.解答题:
16.(10分)解关于的二元一次方程组并讨论解的情况. 21世纪教育网
【解】 ……………………………?-……………………………2分………………………………4分
(1)当时,方程组有唯一解,…21世纪教育网…………………………………………6分
(2) 当时,方程组有无穷多组解,……………………………………8分
(3)当时,方程组无解. …………………………………………………………………10分
17.(10分)如图,在棱长为2的正方体中,E是BC1的中点.求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示).21世纪教育网
【解】过E作EF⊥BC,交BC于F,连接DF.
∵ EF⊥平面ABCD,
∴ ∠EDF是直线DE与平面ABCD所成的角. ……………4分
由题意,得EF=
∵ …………………………..6分
∵ EF⊥DF, ∴ ……………..8分
故直线DE与平面ABCD所成角的大小是….10分
18.(11分)已知向量
(Ⅰ)求向量的长度的最大值;21世纪教育网
(Ⅱ)设,且,求的值。
【解】(1)则……4分
,即 21世纪教育网
当时,有所以向量的长度的最大值为2.……………………5分
(2)解法1:由已知可得
。
,,即。……………………………………8分21世纪教育网
由,得,即。
,于是。………………………11分21世纪教育网
解法2:若,则,又由,得
,,即……………………………………8分21世纪教育网
,平方后化简得
解得或,经检验,即为所求……………………11分
19 .(12分)已知数列的前项和为,,且(为正整数).
(1)求数列的通项公式;21世纪教育网
(2)记.若对任意正整数,恒成立,求实数的最大值.
【解】(1), ①
当时,. ②
由 ① - ②,得.
……………………………………………………………………… 3分
又 ,,解得 .…………………………………………… 4分21世纪教育网
数列是首项为1,公比为的等比数列.
(为正整数). ………………………………………………… 6分21世纪教育网
(2)由(1)知,,. ……………… 8分21世纪教育网
由题意可知,对于任意的正整数,恒有,解得 .………10分
数列单调递增, 当时,数列中的最小项为,
必有,即实数的最大值为.…………………………………………………… 12分
20.(12分)在直角坐标平面上的一列点简记为.若由构成的数列满足其中为方向与轴正方向相同的单位向量,则称为点列. 21世纪教育网
(1)判断是否为点列,并说明理由;
(2)若为点列,且点在点的右上方.任取其中连续三点判断的形状(锐角三角形、直角三角形、钝角三角形),并予以证明;
(3)若为点列,正整数满足求证:21世纪教育网
【解】(1) , ,显然有,
是点列. ………………………………………………………………………… 3分
(2)在△中,,
.………………………………………… 5分
点在点的右上方,,
为点列,,
,则.
为钝角, △为钝角三角形.……………………………… 7分21世纪教育网
(3)[证明] ,. ①
. ②
同理. ③ ……………………………… 10分
由于为点列,于是,④
由①、②、③、④可推得
,,
即 . …………………………………………………………………… 12分21世纪教育网
同课章节目录
