人教版五年级下册6《分数的加法和减法》课件(共78张PPT)
文档属性
| 名称 | 人教版五年级下册6《分数的加法和减法》课件(共78张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-22 20:02:19 | ||
图片预览








文档简介
(共78张PPT)
第1课时 同分母分数加、减法
人教版数学五年级下册课件
6 分数的加法和减法
—
是( )个
4
是( )个
3
是( )个
5
复习导入
3
4
—
1
4
—
4
9
—
1
9
—
5
7
—
1
7
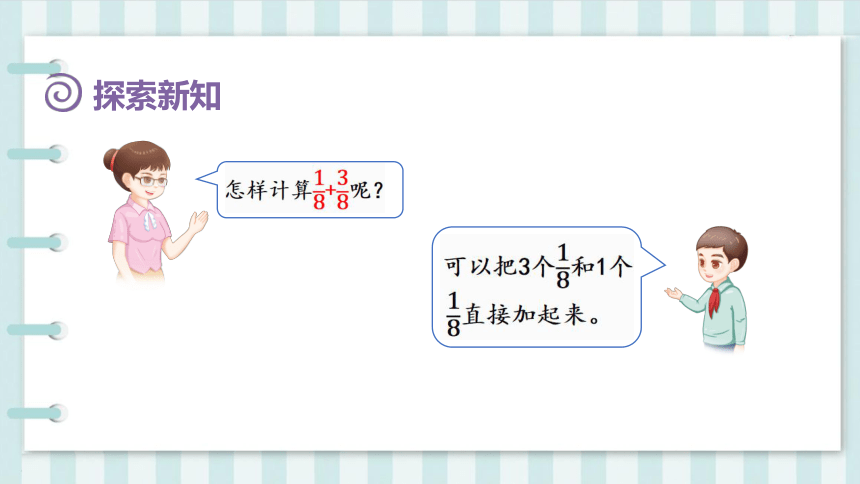
爸爸吃 张饼,妈妈吃 张饼。
探索新知
探究点1 同分母分数加法的计算方法
(1)爸爸和妈妈一共吃多少张饼?
求爸爸和妈妈一共吃了多少张饼,就是求 和 这两个数的和 , 用加法计算 , 列式为 + 。
探索新知
(1)爸爸和妈妈一共吃多少张饼?
你有什么发现呢?
—
1
8
—
3
8
+
探索新知
是1个是3个1个加3个
是4个也就是即+=。
探索新知
—
4
8
=
2
1
计算方法推导:
探索新知
在计算同分母分数加法时,分母不变,分子相加。计算结果,能约分的要约成最简分数。
约分
最简分数
—
3
8
—
1
8
+
分子相加
分母不变
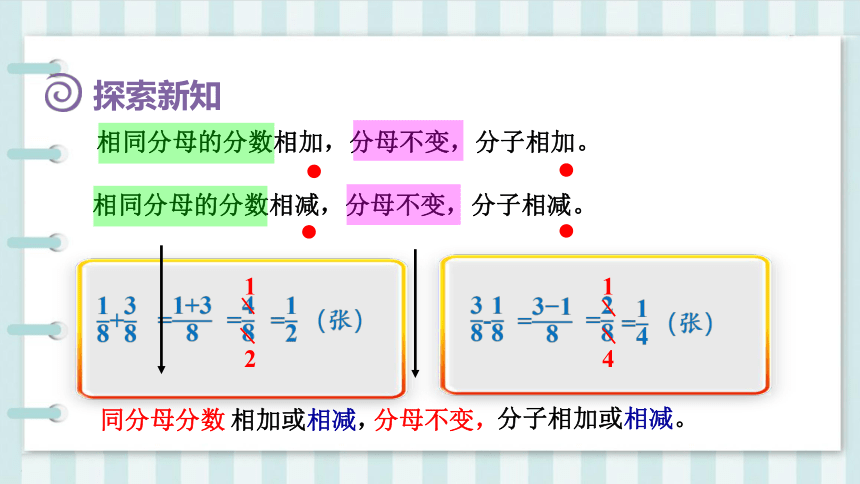
答: 爸爸和妈妈一共吃了 张饼。
—
1
2
1+3
8
——
=
—
1
2
(张)
=
探索新知
探究点2 同分母分数减法的计算方法
(2)爸爸比妈妈多吃多少张饼?
求爸爸比妈妈多吃了多少张饼,就是从爸爸吃的饼中去掉妈妈吃的饼,用减法计算,列式为
怎样计算 呢?
计算方法推导:
探索新知
同分母分数相减,分母不变,分子相减。
约分
最简分数
=
-
=
=
4
1
分子相减
分母不变
答:爸爸比妈妈多吃了 张饼。
=
-
=
=
4
1
+
=
=
=
2
1
相同分母的分数相加,分母不变,分子相加。
相同分母的分数相减,分母不变,分子相减。
同分母分数
相加或相减,
分母不变,
分子相加或相减。
探索新知
小试牛刀
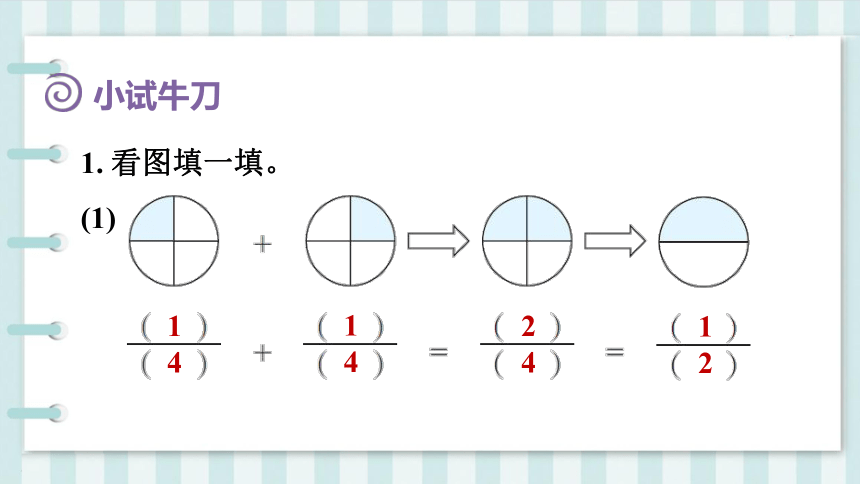
1. 看图填一填。
(1)
1
4
1
4
2
4
1
2
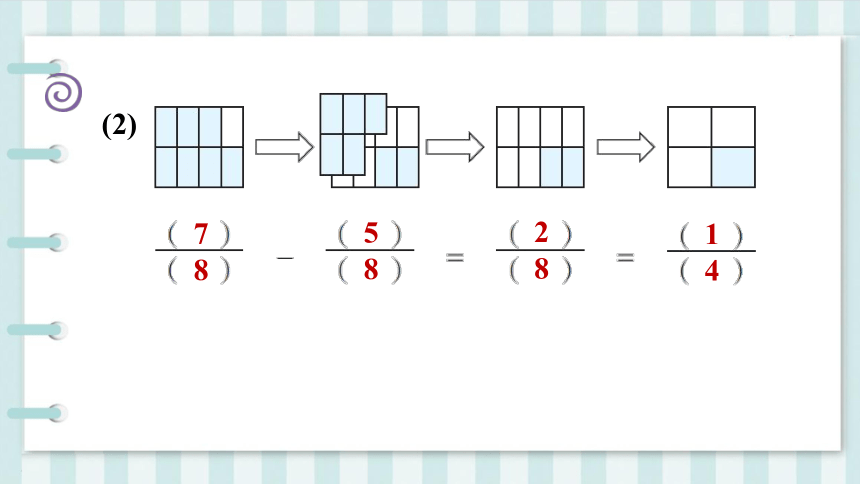
(2)
7
8
5
8
2
8
1
4
2. 算一算。
1
1
3. 在括号里填上适当的数。
当堂练习
1. (易错题) 在括号里填上不同的数, 使每个分数都是最简分数。(答案不唯一)
1
2
19
填空时要注意括号里的数与15要互质。
+
=
=
=
2
1
=
-
=
=
4
1
同分母分数相加、减,分母不变,只把分子相加、减。
计算的结果,能约分的要约成最简分数。
同分母分数加、减法的计算法则:
课堂总结
第2课时 异分母分数加、 减法
人教版数学五年级下册课件
6 分数的加法和减法
1.同分母分数加、减法怎样计算?
2.计算中要注意什么?
8
5
=
+
8
1
8
1
5
+
=
=
4
3
4
8
6
=
9
7
-
9
2
9
2
7
-
=
9
5
30
30
-
30
11
=
30
11
30
-
=
30
19
=
1
-
30
11
4
1
=
+
4
4
4
1
3
复习导入
同分母分数相加、减,分母不变,只把分子相加、减。
计算的结果,能约分的要约成最简分数。
某小区生活垃圾分类统计情况如右图。
探索新知
(1)有害垃圾和其他垃圾在生活垃圾中
共占几分之几?
探究点1 异分母分数加法的计算方法
1
8
—
+ =_____
1
4
—
探索新知
和的分母不同,也就是分数单位不同,不能直接相加。怎么办呢?
我们可以把它们转化为同分母分数再相加。
探索新知
分母不同的分数,要先通分才能相加。
1
8
—
+ =
1
4
—
1
8
—
+ =
2
8
—
3
8
—
(2)可回收物多还是厨余垃圾多?
它们的差占生活垃圾总量的几分之几?
探索新知
探究点2 异分母分数减法的计算方法
利用通分把它们化成同分母的分数, 40和20的最小公倍数是40, 把它们化成分母是40的分数。
19
40
—
- =
3
20
—
探索新知
3
20
—
<
19
40
—
19
40
—
- =
3
20
—
19
40
—
- =
6
40
—
13
40
—
答: 厨余垃圾多, 它们的差占生活垃圾总量的 。
13
40
—
异分母分数减法的计算方法:
异分母分数相加、减, 先通分,再按照同分母分数加、减法进行计算。
(1) + = + = (2) - = - =
探索新知
小试牛刀
1. 填一填。
(1)
1
2
1
4
2
4
1
4
3
4
(2)
1
2
1
3
3
6
2
6
1
6
分数单位
通分
2. 计算下列各题。
当堂练习
+
1. 在 里填上适当的运算符号。
-
-
+
2. 【探究题】计算下面各题并发现其中的规律。
异分母分数相加、减,先通分,把它们化成同分母的分数,再按照同分母分数加、减法的法则进行计算。
课堂总结
第3课时 分数加减混合运算
人教版数学五年级下册课件
6 分数的加法和减法
新课导入
同学们,你们喜欢旅游吗?图片呈现的是森林公园,让我们一起探索其中的数学问题吧。
探索新知
植被类型 占公园面积的几分之几
乔木林
灌木林
草地
某森林公园植被情况如下表。
你能提出哪些
数学问题?
森林部分比草地部分多占公园面积的几分之几?
探究点1 分数加减混合运算的运算顺序和计算方法
条件
问题
乔木林:
灌木林
草地
森林部分比草地部分多占公园面积的几分之几?
森林部分
就是求乔木林和灌木林的面积之和比草地面积多占公园面积的几分之几。
列式:
探索新知
8 1
10 5
= +
—
—
【方法一:分步通分法】
分数加减混合运算的顺序和整数加减混合运算的顺序相同,没有括号的,按从左到右的顺序计算。
5
4
探索新知
1 3 1
2 10 5
+ -
—
—
—
5 3 1
10 10 5
= + -
—
—
—
3
5
=
—
1 3
2 10
+
—
—
先算:
1 3
2 10
和 通分
—
—
3
5
=
—
6
10
=
—
【方法二:一次通分法】
5
3
三个分数是异分母分数的加减混合运算,可以分步通分也可以一次性通分进行计算。计算时,
可以根据题目的特点和自己的
情况灵活选择方法。
探索新知
8 2
10 10
= -
—
—
1 3 1
2 10 5
+ -
—
—
—
5 3 2
10 10 10
= + -
—
—
—
探索新知
(2)森林和裸露地面降水转化情况如下表。
类型 储存为 地下水 地表水 其他
森林
裸露地面
1
4
7
20
2
5
11
20
2
5
( )
( )
裸露地面储存的地下水占降水的几分之几?
探究点2 带括号的分数加减混合运算
【小红这样算】
1--
=--
=-
=
【小亮这样算】
1-
=1-
=1-
=
答:裸露地面储存的地下水占降水的。
这两种方法有什么不同呢?
探索新知
你能说一说分数加减混合运算的运算顺序吗?
分数加减混合运算的运算顺序与整数加减混合
运算的运算顺序相同:
(1)在没有括号的运算中,按照从左到右的顺序
进行计算;
(2)在有括号的运算中,要先算括号里面的,再
算括号外面的。
探索新知
小试牛刀
先口述运算顺序, 再计算。(口述运算顺序略)
=
=
=
=
=
=
当堂练习
1. 在 里填上适当的数, 使每个正方形四个角上的数加起来都等于1。
注意完成数学作业所用时间未知,计算时用减法。
分数加减混合运算的运算顺序与整数加减混合运算的运算顺序相同,没有括号的,按照从左到右的顺序依次计算;有括号的要先算括号里面的。
课堂总结
第4课时 整数加法的运算律
推广到分数加法
人教版数学五年级下册课件
6 分数的加法和减法
53+36+47
= 53+47+36
= 1.5+(3.8+6.2)
加法交换律:a + b = b + a
加法结合律:(a + b)+ c = a +(b + c)
1.5+3.8+6.2
= 136
用简便方法计算下面各题,并说出简算的依据。
复习导入
=11.5
请你说一说式中的字母可以表示什么数?
可以表示整数、小数。
探索新知
探究点 分数加法的运算律及应用
下面每组算式的左右两边有什么样的关系?
2
5
+
3
7
3
7
+
2
5
( + ) +
1
4
3
4
2
3
+ ( + )
1
4
3
4
2
3
=
=
猜想一下 里应该填什么符号?
探索新知
( + ) +
1
4
3
4
2
3
+ ( + )
1
4
3
4
2
3
观察这些算式,你发现了什么?
2
5
+
3
7
3
7
+
2
5
=
=
第一个算式左右两边的数都一样,就是交换了位置,很像整数中的加法交换律。
a + b = b + a
探索新知
( + ) +
1
4
3
4
2
3
+ ( + )
1
4
3
4
2
3
=
第二个算式只是改变了加的顺序,很像加法结合律。
(a + b)+ c = a +(b + c)
整数加法的交换律和结合律对分数加法同样适用。利用运算律可以使一些分数计算变得简便。
探索新知
探索新知
请你再举几个分数加法的例子来验证一下,看看我们得出的结论是否正确。
小试牛刀
用简便方法计算。
当堂练习
4
5
5
6
2. 口算。
根据以上规律简算。
整数加法的交换律和结合律对分数加法同样适用,利用运算律可以使一些分数加法计算变得简便。
课堂总结
第5课时 分数加、减法的应用
人教版数学五年级下册课件
6 分数的加法和减法
谈话导入
同学们,你们喜欢喝果汁吗 乐乐很喜欢喝果汁,他在喝果汁时遇到了数学问题,今天我们就来研究喝果汁中的学问。
一杯纯果汁,小乐喝了半杯后,觉得有些甜,就兑满了水。他又喝了半杯,就出去玩了。小乐一共喝了多少杯纯果汁?多少杯水?
探索新知
探究点 分数加减法的应用
阅读与理解
第一次:一杯纯果汁,喝了______杯。
第二次:兑满水,又喝了______杯。
1
2
1
2
问题:一共喝了多少杯纯果汁?多少杯水?
分析与解答
示意图分析
喝了半杯
兑满水
又喝了一半
探索新知
表格分析
第一次 第二次
喝掉的果汁
剩下的果汁
喝掉的水
一杯果汁的一半
半杯果汁的一半
一杯果汁的一半
半杯果汁的一半
半杯水的一半
0
探索新知
线段图分析
第一次剩下的果汁
剩下的果汁
喝掉的果汁
兑入的水
喝掉的果汁
喝掉的水
第二次
第一次
探索新知
探索新知
第一次喝了
杯纯果汁。
1
2
兑满水,水是
杯,纯果汁还是 杯 。
1
2
1
2
又喝了 杯,这 杯里,一半是纯果汁,
一半是水。
1
2
1
2
探索新知
杯的一半是_____杯。
1
2
第二次喝的纯果汁是_____杯,水是_____杯。
一共喝的纯果汁:________________
水:_________
1
4
1
4
1
4
1
4
杯
1
2
1
4
+
3
4
=
(杯)
回顾与反思
1. 解决这道题的关键是什么?
每次喝的半杯中都是剩下纯果汁的一半,第一次喝的是整杯纯果汁的一半,第二次喝的是剩下半杯纯果汁的一半。
探索新知
2. 关键步骤利用了什么知识?
分数的意义、分数加减法、画图法等知识。
3. 我们利用画图法得出的结论到底对不对呢?可以怎样检验?
可以从剩下的半杯兑过水的果汁考虑:剩下的 杯中有一半的纯果汁和一半的水,所以剩下的纯果汁是 杯,所以喝了 杯纯果汁是正确的。
1
2
1
4
3
4
探索新知
小试牛刀
1. 填一填。
(1) 一杯果汁, 第一次喝去半杯后, 用水加满; 第二次喝去半杯后, 又用水加满; 第三次全部喝完。一共喝了( ) 杯果汁和( ) 杯水。
1
1
(2) 陈叔叔冲了一杯咖啡, 第一次喝了半杯, 第二次喝了剩下的一半, 最后剩下这杯咖啡的( ) 。(填分数)
2. 一杯奶茶, 华华喝了半杯后, 觉得太甜, 就兑满了水。又喝了半杯, 就做作业去了。她一共喝了多少杯奶茶 多少杯水 看图分析:
一共喝的奶茶: _________________
喝的水: _______________________
当堂练习
解题时要注意纯牛奶的总量不变,加的都是水。
1.运用分数的意义、分数加减法、画图法等
知识解决实际问题。
2.解决问题的关键是理解题意。
课堂总结
第1课时 同分母分数加、减法
人教版数学五年级下册课件
6 分数的加法和减法
—
是( )个
4
是( )个
3
是( )个
5
复习导入
3
4
—
1
4
—
4
9
—
1
9
—
5
7
—
1
7
爸爸吃 张饼,妈妈吃 张饼。
探索新知
探究点1 同分母分数加法的计算方法
(1)爸爸和妈妈一共吃多少张饼?
求爸爸和妈妈一共吃了多少张饼,就是求 和 这两个数的和 , 用加法计算 , 列式为 + 。
探索新知
(1)爸爸和妈妈一共吃多少张饼?
你有什么发现呢?
—
1
8
—
3
8
+
探索新知
是1个是3个1个加3个
是4个也就是即+=。
探索新知
—
4
8
=
2
1
计算方法推导:
探索新知
在计算同分母分数加法时,分母不变,分子相加。计算结果,能约分的要约成最简分数。
约分
最简分数
—
3
8
—
1
8
+
分子相加
分母不变
答: 爸爸和妈妈一共吃了 张饼。
—
1
2
1+3
8
——
=
—
1
2
(张)
=
探索新知
探究点2 同分母分数减法的计算方法
(2)爸爸比妈妈多吃多少张饼?
求爸爸比妈妈多吃了多少张饼,就是从爸爸吃的饼中去掉妈妈吃的饼,用减法计算,列式为
怎样计算 呢?
计算方法推导:
探索新知
同分母分数相减,分母不变,分子相减。
约分
最简分数
=
-
=
=
4
1
分子相减
分母不变
答:爸爸比妈妈多吃了 张饼。
=
-
=
=
4
1
+
=
=
=
2
1
相同分母的分数相加,分母不变,分子相加。
相同分母的分数相减,分母不变,分子相减。
同分母分数
相加或相减,
分母不变,
分子相加或相减。
探索新知
小试牛刀
1. 看图填一填。
(1)
1
4
1
4
2
4
1
2
(2)
7
8
5
8
2
8
1
4
2. 算一算。
1
1
3. 在括号里填上适当的数。
当堂练习
1. (易错题) 在括号里填上不同的数, 使每个分数都是最简分数。(答案不唯一)
1
2
19
填空时要注意括号里的数与15要互质。
+
=
=
=
2
1
=
-
=
=
4
1
同分母分数相加、减,分母不变,只把分子相加、减。
计算的结果,能约分的要约成最简分数。
同分母分数加、减法的计算法则:
课堂总结
第2课时 异分母分数加、 减法
人教版数学五年级下册课件
6 分数的加法和减法
1.同分母分数加、减法怎样计算?
2.计算中要注意什么?
8
5
=
+
8
1
8
1
5
+
=
=
4
3
4
8
6
=
9
7
-
9
2
9
2
7
-
=
9
5
30
30
-
30
11
=
30
11
30
-
=
30
19
=
1
-
30
11
4
1
=
+
4
4
4
1
3
复习导入
同分母分数相加、减,分母不变,只把分子相加、减。
计算的结果,能约分的要约成最简分数。
某小区生活垃圾分类统计情况如右图。
探索新知
(1)有害垃圾和其他垃圾在生活垃圾中
共占几分之几?
探究点1 异分母分数加法的计算方法
1
8
—
+ =_____
1
4
—
探索新知
和的分母不同,也就是分数单位不同,不能直接相加。怎么办呢?
我们可以把它们转化为同分母分数再相加。
探索新知
分母不同的分数,要先通分才能相加。
1
8
—
+ =
1
4
—
1
8
—
+ =
2
8
—
3
8
—
(2)可回收物多还是厨余垃圾多?
它们的差占生活垃圾总量的几分之几?
探索新知
探究点2 异分母分数减法的计算方法
利用通分把它们化成同分母的分数, 40和20的最小公倍数是40, 把它们化成分母是40的分数。
19
40
—
- =
3
20
—
探索新知
3
20
—
<
19
40
—
19
40
—
- =
3
20
—
19
40
—
- =
6
40
—
13
40
—
答: 厨余垃圾多, 它们的差占生活垃圾总量的 。
13
40
—
异分母分数减法的计算方法:
异分母分数相加、减, 先通分,再按照同分母分数加、减法进行计算。
(1) + = + = (2) - = - =
探索新知
小试牛刀
1. 填一填。
(1)
1
2
1
4
2
4
1
4
3
4
(2)
1
2
1
3
3
6
2
6
1
6
分数单位
通分
2. 计算下列各题。
当堂练习
+
1. 在 里填上适当的运算符号。
-
-
+
2. 【探究题】计算下面各题并发现其中的规律。
异分母分数相加、减,先通分,把它们化成同分母的分数,再按照同分母分数加、减法的法则进行计算。
课堂总结
第3课时 分数加减混合运算
人教版数学五年级下册课件
6 分数的加法和减法
新课导入
同学们,你们喜欢旅游吗?图片呈现的是森林公园,让我们一起探索其中的数学问题吧。
探索新知
植被类型 占公园面积的几分之几
乔木林
灌木林
草地
某森林公园植被情况如下表。
你能提出哪些
数学问题?
森林部分比草地部分多占公园面积的几分之几?
探究点1 分数加减混合运算的运算顺序和计算方法
条件
问题
乔木林:
灌木林
草地
森林部分比草地部分多占公园面积的几分之几?
森林部分
就是求乔木林和灌木林的面积之和比草地面积多占公园面积的几分之几。
列式:
探索新知
8 1
10 5
= +
—
—
【方法一:分步通分法】
分数加减混合运算的顺序和整数加减混合运算的顺序相同,没有括号的,按从左到右的顺序计算。
5
4
探索新知
1 3 1
2 10 5
+ -
—
—
—
5 3 1
10 10 5
= + -
—
—
—
3
5
=
—
1 3
2 10
+
—
—
先算:
1 3
2 10
和 通分
—
—
3
5
=
—
6
10
=
—
【方法二:一次通分法】
5
3
三个分数是异分母分数的加减混合运算,可以分步通分也可以一次性通分进行计算。计算时,
可以根据题目的特点和自己的
情况灵活选择方法。
探索新知
8 2
10 10
= -
—
—
1 3 1
2 10 5
+ -
—
—
—
5 3 2
10 10 10
= + -
—
—
—
探索新知
(2)森林和裸露地面降水转化情况如下表。
类型 储存为 地下水 地表水 其他
森林
裸露地面
1
4
7
20
2
5
11
20
2
5
( )
( )
裸露地面储存的地下水占降水的几分之几?
探究点2 带括号的分数加减混合运算
【小红这样算】
1--
=--
=-
=
【小亮这样算】
1-
=1-
=1-
=
答:裸露地面储存的地下水占降水的。
这两种方法有什么不同呢?
探索新知
你能说一说分数加减混合运算的运算顺序吗?
分数加减混合运算的运算顺序与整数加减混合
运算的运算顺序相同:
(1)在没有括号的运算中,按照从左到右的顺序
进行计算;
(2)在有括号的运算中,要先算括号里面的,再
算括号外面的。
探索新知
小试牛刀
先口述运算顺序, 再计算。(口述运算顺序略)
=
=
=
=
=
=
当堂练习
1. 在 里填上适当的数, 使每个正方形四个角上的数加起来都等于1。
注意完成数学作业所用时间未知,计算时用减法。
分数加减混合运算的运算顺序与整数加减混合运算的运算顺序相同,没有括号的,按照从左到右的顺序依次计算;有括号的要先算括号里面的。
课堂总结
第4课时 整数加法的运算律
推广到分数加法
人教版数学五年级下册课件
6 分数的加法和减法
53+36+47
= 53+47+36
= 1.5+(3.8+6.2)
加法交换律:a + b = b + a
加法结合律:(a + b)+ c = a +(b + c)
1.5+3.8+6.2
= 136
用简便方法计算下面各题,并说出简算的依据。
复习导入
=11.5
请你说一说式中的字母可以表示什么数?
可以表示整数、小数。
探索新知
探究点 分数加法的运算律及应用
下面每组算式的左右两边有什么样的关系?
2
5
+
3
7
3
7
+
2
5
( + ) +
1
4
3
4
2
3
+ ( + )
1
4
3
4
2
3
=
=
猜想一下 里应该填什么符号?
探索新知
( + ) +
1
4
3
4
2
3
+ ( + )
1
4
3
4
2
3
观察这些算式,你发现了什么?
2
5
+
3
7
3
7
+
2
5
=
=
第一个算式左右两边的数都一样,就是交换了位置,很像整数中的加法交换律。
a + b = b + a
探索新知
( + ) +
1
4
3
4
2
3
+ ( + )
1
4
3
4
2
3
=
第二个算式只是改变了加的顺序,很像加法结合律。
(a + b)+ c = a +(b + c)
整数加法的交换律和结合律对分数加法同样适用。利用运算律可以使一些分数计算变得简便。
探索新知
探索新知
请你再举几个分数加法的例子来验证一下,看看我们得出的结论是否正确。
小试牛刀
用简便方法计算。
当堂练习
4
5
5
6
2. 口算。
根据以上规律简算。
整数加法的交换律和结合律对分数加法同样适用,利用运算律可以使一些分数加法计算变得简便。
课堂总结
第5课时 分数加、减法的应用
人教版数学五年级下册课件
6 分数的加法和减法
谈话导入
同学们,你们喜欢喝果汁吗 乐乐很喜欢喝果汁,他在喝果汁时遇到了数学问题,今天我们就来研究喝果汁中的学问。
一杯纯果汁,小乐喝了半杯后,觉得有些甜,就兑满了水。他又喝了半杯,就出去玩了。小乐一共喝了多少杯纯果汁?多少杯水?
探索新知
探究点 分数加减法的应用
阅读与理解
第一次:一杯纯果汁,喝了______杯。
第二次:兑满水,又喝了______杯。
1
2
1
2
问题:一共喝了多少杯纯果汁?多少杯水?
分析与解答
示意图分析
喝了半杯
兑满水
又喝了一半
探索新知
表格分析
第一次 第二次
喝掉的果汁
剩下的果汁
喝掉的水
一杯果汁的一半
半杯果汁的一半
一杯果汁的一半
半杯果汁的一半
半杯水的一半
0
探索新知
线段图分析
第一次剩下的果汁
剩下的果汁
喝掉的果汁
兑入的水
喝掉的果汁
喝掉的水
第二次
第一次
探索新知
探索新知
第一次喝了
杯纯果汁。
1
2
兑满水,水是
杯,纯果汁还是 杯 。
1
2
1
2
又喝了 杯,这 杯里,一半是纯果汁,
一半是水。
1
2
1
2
探索新知
杯的一半是_____杯。
1
2
第二次喝的纯果汁是_____杯,水是_____杯。
一共喝的纯果汁:________________
水:_________
1
4
1
4
1
4
1
4
杯
1
2
1
4
+
3
4
=
(杯)
回顾与反思
1. 解决这道题的关键是什么?
每次喝的半杯中都是剩下纯果汁的一半,第一次喝的是整杯纯果汁的一半,第二次喝的是剩下半杯纯果汁的一半。
探索新知
2. 关键步骤利用了什么知识?
分数的意义、分数加减法、画图法等知识。
3. 我们利用画图法得出的结论到底对不对呢?可以怎样检验?
可以从剩下的半杯兑过水的果汁考虑:剩下的 杯中有一半的纯果汁和一半的水,所以剩下的纯果汁是 杯,所以喝了 杯纯果汁是正确的。
1
2
1
4
3
4
探索新知
小试牛刀
1. 填一填。
(1) 一杯果汁, 第一次喝去半杯后, 用水加满; 第二次喝去半杯后, 又用水加满; 第三次全部喝完。一共喝了( ) 杯果汁和( ) 杯水。
1
1
(2) 陈叔叔冲了一杯咖啡, 第一次喝了半杯, 第二次喝了剩下的一半, 最后剩下这杯咖啡的( ) 。(填分数)
2. 一杯奶茶, 华华喝了半杯后, 觉得太甜, 就兑满了水。又喝了半杯, 就做作业去了。她一共喝了多少杯奶茶 多少杯水 看图分析:
一共喝的奶茶: _________________
喝的水: _______________________
当堂练习
解题时要注意纯牛奶的总量不变,加的都是水。
1.运用分数的意义、分数加减法、画图法等
知识解决实际问题。
2.解决问题的关键是理解题意。
课堂总结
