2025年中考数学二轮复习-专题17规律猜想归纳问题 课件(共23张PPT)
文档属性
| 名称 | 2025年中考数学二轮复习-专题17规律猜想归纳问题 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 634.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-23 08:57:39 | ||
图片预览






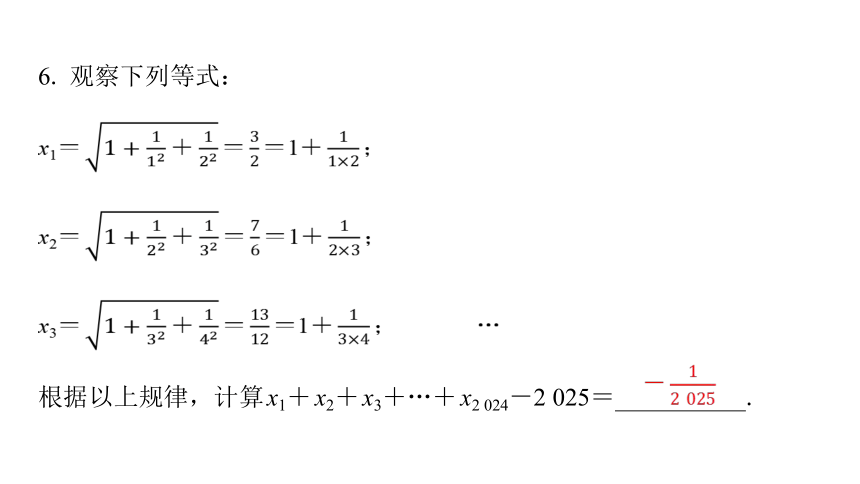
文档简介
(共23张PPT)
专题十七 规律猜想归纳问题
类型一 数列(阵)规律
在进行数列、数阵的规律探索时,要从后项与前项差的变化、后
项与前项商的变化、各项乘方的变化等角度观察思考数列的变化规律.
有时还要兼顾序号的奇偶性或周期性进行分析.
1. 按一定规律排列的单项式:x3,-x5,x7,-x9,x11,…,则第n个
单项式是( C )
A. (-1)n-1x2n-1 B. (-1)nx2n-1
C. (-1)n-1x2n+1 D. (-1)2x2n+1
C
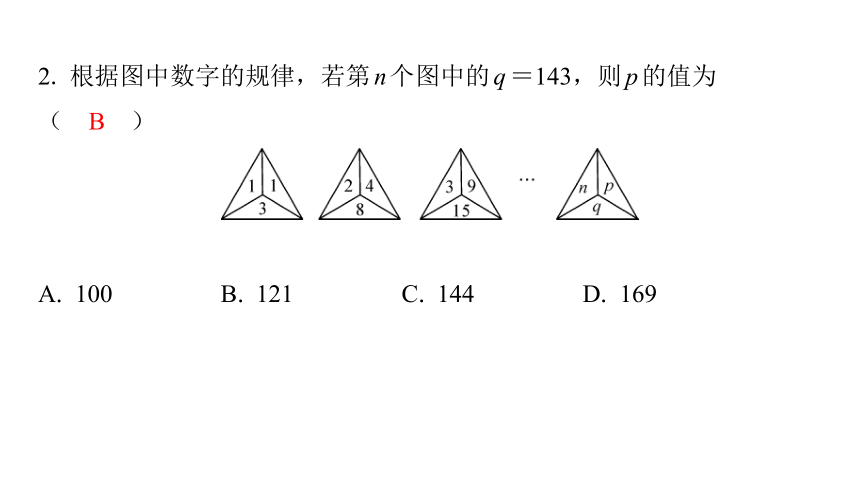
2. 根据图中数字的规律,若第n个图中的q=143,则p的值为
( B )
A. 100 B. 121 C. 144 D. 169
B
3. [2024·德阳]将一组数 ,2, ,2 , ,2 ,…,
,…,按如图方式进行排列,则第八行左起第1个数是( C )
C
4. 某种细胞可通过分裂来繁殖后代,我们就用数学模型2n来表示.即21
=2,22=4,23=8,24=16,25=32,…,请你推算22 025的个位数字是
( D )
A. 8 B. 6 C. 4 D. 2
D
5. 已知有理数a≠1,我们把 称为a的差倒数.例如:2的差倒数是
=-1,-1的差倒数是 = .如果a1=-2,a2是a1的差倒
数,a3是a2的差倒数,a4是a3的差倒数……依此类推,那么a1+a2+…
+a100的值是( A )
A
6. 观察下列等式:
x1= = =1+ ;
x2= = =1+ ;
x3= = =1+ ; …
根据以上规律,计算x1+x2+x3+…+x2 024-2 025= .
-
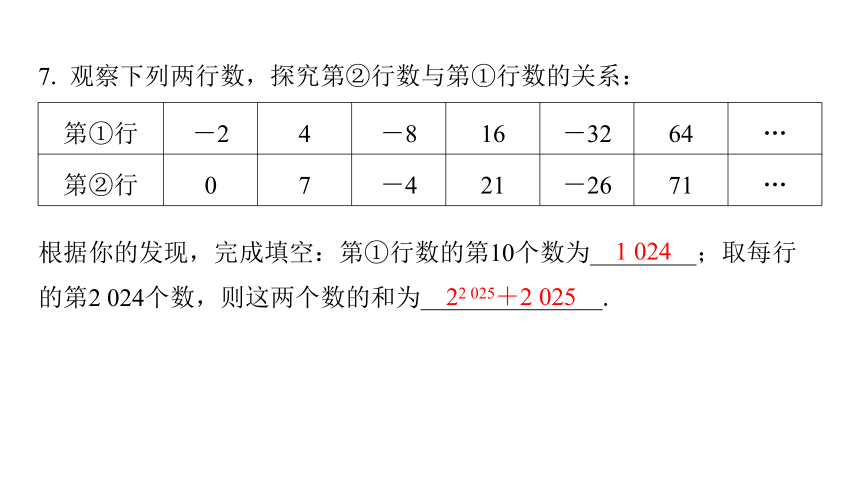
7. 观察下列两行数,探究第②行数与第①行数的关系:
第①行 -2 4 -8 16 -32 64 …
第②行 0 7 -4 21 -26 71 …
根据你的发现,完成填空:第①行数的第10个数为 ;取每行
的第2 024个数,则这两个数的和为 .
1 024
22 025+2 025
8. [2024·遂宁]在等边三角形ABC三边上分别取点D,E,F,使得AD
=BE=CF,连接三点得到△DEF,易得△ADF≌△BED≌△CFE,
设S△ABC=1,则S△DEF=1-3S△ADF.
如图①,当 = 时,S△DEF=1-3× = ;
如图②,当 = 时,S△DEF=1-3× = ;
如图③,当 = 时,S△DEF=1-3× = ;
……
直接写出,当 = 时,S△DEF= .
9. 如图,将从1开始的连续自然数按如图方式排列,若有序数对(n,
m)表示第n行,从左到右第m个数,如(3,2)表示6,则表示99的有
序数对是 .
(10,18)
10. [2024·潍坊]将连续的正整数排成如图所示的数表.记a(i,j)为数表
中第i行第j列位置的数字,如a(1,2)=4,a(3,1)=9,a(5,4)=22.
若a(m,n)=2 024,则m= ,n= .
45
2
类型二 图形变化规律
先根据图形变化依次计数或结合几何知识依次计算,将其图形变
化规律转化成对应的数列变化,再从数列的变化角度猜想归纳,注意
运用从特殊到一般的思想.
1. 用长度相同的木棍按如图所示的规律拼图案,拼第①个图案用了9根
木棍,拼第②个图案用了14根木棍,拼第③个图案用了19根木棍……按
此规律拼下去,则拼第⑧个图案用的木棍根数是 .
44
2. 如图,根据“勾股树”生长规律,第六代勾股树中正方形的个数
为 .
127
3. 如图,由12个有公共顶点O的直角三角形拼成图案,∠AOB=
∠BOC=∠COD=…=∠LOM=30°.若S△AOB=1,则图中与△AOB
位似的三角形的面积为 .
4. 如图,四边形ABCD是边长为1的正方形,分别以A,B,C,D为
圆心,AD,BA1,CB1,DC1为半径作90°的圆弧……如此循环下去,
的长为 (结果保留π).
4 048π
5. 如图,在边长为1的菱形ABCD中,∠DAB=60°.连接对角线AC,
以AC为边作第二个菱形ACEF,使∠FAC=60°;连接AE,再以AE
为边作第三个菱形AEGH,使∠HAE=60°……按此规律所作的第n个
菱形的边长是 .
( )n-1
6. 如图,平面直角坐标系中,点A1,A2,A3,A4,…,在x轴的正半
轴上,点B1,B2,B3,B4,…,在直线y= x(x≥0)上.若点A1的
坐标为(2,0),且△A1B1A2,△A2B2A3,△A3B3A4,…,均为等边三
角形,则点B2 024的纵坐标为 .
×22 023
7. [2024·内江]如图,在平面直角坐标系中,AB⊥y轴,垂足为B,将
△ABO绕点A逆时针旋转到△AB1O1的位置,使点B的对应点B1落在直
线y=- x上,再将△AB1O1绕点B1逆时针旋转到△ O2的位置,使
点O1的对应点O2也落在直线y=- x上,如此下去……若点B的坐标为
(0,3),则点B37的坐标为( C )
A. (180,135) B. (180,133)
C. (-180,135) D. (-180,133)
C
8. [2024·广安]已知,直线l:y= x- 与x轴相交于点A1,以OA1为
边作等边三角形OA1B1,点B1在第一象限内,过点B1作x轴的平行线与
直线l交于点A2,与y轴交于点C1,以C1A2为边作等边三角形C1A2B2
(点B2在点B1的上方),以同样的方式依次作等边三角形C2A3B3,等
边三角形C3A4B4……则点A2 024的横坐标为 .
谢谢观看
专题十七 规律猜想归纳问题
类型一 数列(阵)规律
在进行数列、数阵的规律探索时,要从后项与前项差的变化、后
项与前项商的变化、各项乘方的变化等角度观察思考数列的变化规律.
有时还要兼顾序号的奇偶性或周期性进行分析.
1. 按一定规律排列的单项式:x3,-x5,x7,-x9,x11,…,则第n个
单项式是( C )
A. (-1)n-1x2n-1 B. (-1)nx2n-1
C. (-1)n-1x2n+1 D. (-1)2x2n+1
C
2. 根据图中数字的规律,若第n个图中的q=143,则p的值为
( B )
A. 100 B. 121 C. 144 D. 169
B
3. [2024·德阳]将一组数 ,2, ,2 , ,2 ,…,
,…,按如图方式进行排列,则第八行左起第1个数是( C )
C
4. 某种细胞可通过分裂来繁殖后代,我们就用数学模型2n来表示.即21
=2,22=4,23=8,24=16,25=32,…,请你推算22 025的个位数字是
( D )
A. 8 B. 6 C. 4 D. 2
D
5. 已知有理数a≠1,我们把 称为a的差倒数.例如:2的差倒数是
=-1,-1的差倒数是 = .如果a1=-2,a2是a1的差倒
数,a3是a2的差倒数,a4是a3的差倒数……依此类推,那么a1+a2+…
+a100的值是( A )
A
6. 观察下列等式:
x1= = =1+ ;
x2= = =1+ ;
x3= = =1+ ; …
根据以上规律,计算x1+x2+x3+…+x2 024-2 025= .
-
7. 观察下列两行数,探究第②行数与第①行数的关系:
第①行 -2 4 -8 16 -32 64 …
第②行 0 7 -4 21 -26 71 …
根据你的发现,完成填空:第①行数的第10个数为 ;取每行
的第2 024个数,则这两个数的和为 .
1 024
22 025+2 025
8. [2024·遂宁]在等边三角形ABC三边上分别取点D,E,F,使得AD
=BE=CF,连接三点得到△DEF,易得△ADF≌△BED≌△CFE,
设S△ABC=1,则S△DEF=1-3S△ADF.
如图①,当 = 时,S△DEF=1-3× = ;
如图②,当 = 时,S△DEF=1-3× = ;
如图③,当 = 时,S△DEF=1-3× = ;
……
直接写出,当 = 时,S△DEF= .
9. 如图,将从1开始的连续自然数按如图方式排列,若有序数对(n,
m)表示第n行,从左到右第m个数,如(3,2)表示6,则表示99的有
序数对是 .
(10,18)
10. [2024·潍坊]将连续的正整数排成如图所示的数表.记a(i,j)为数表
中第i行第j列位置的数字,如a(1,2)=4,a(3,1)=9,a(5,4)=22.
若a(m,n)=2 024,则m= ,n= .
45
2
类型二 图形变化规律
先根据图形变化依次计数或结合几何知识依次计算,将其图形变
化规律转化成对应的数列变化,再从数列的变化角度猜想归纳,注意
运用从特殊到一般的思想.
1. 用长度相同的木棍按如图所示的规律拼图案,拼第①个图案用了9根
木棍,拼第②个图案用了14根木棍,拼第③个图案用了19根木棍……按
此规律拼下去,则拼第⑧个图案用的木棍根数是 .
44
2. 如图,根据“勾股树”生长规律,第六代勾股树中正方形的个数
为 .
127
3. 如图,由12个有公共顶点O的直角三角形拼成图案,∠AOB=
∠BOC=∠COD=…=∠LOM=30°.若S△AOB=1,则图中与△AOB
位似的三角形的面积为 .
4. 如图,四边形ABCD是边长为1的正方形,分别以A,B,C,D为
圆心,AD,BA1,CB1,DC1为半径作90°的圆弧……如此循环下去,
的长为 (结果保留π).
4 048π
5. 如图,在边长为1的菱形ABCD中,∠DAB=60°.连接对角线AC,
以AC为边作第二个菱形ACEF,使∠FAC=60°;连接AE,再以AE
为边作第三个菱形AEGH,使∠HAE=60°……按此规律所作的第n个
菱形的边长是 .
( )n-1
6. 如图,平面直角坐标系中,点A1,A2,A3,A4,…,在x轴的正半
轴上,点B1,B2,B3,B4,…,在直线y= x(x≥0)上.若点A1的
坐标为(2,0),且△A1B1A2,△A2B2A3,△A3B3A4,…,均为等边三
角形,则点B2 024的纵坐标为 .
×22 023
7. [2024·内江]如图,在平面直角坐标系中,AB⊥y轴,垂足为B,将
△ABO绕点A逆时针旋转到△AB1O1的位置,使点B的对应点B1落在直
线y=- x上,再将△AB1O1绕点B1逆时针旋转到△ O2的位置,使
点O1的对应点O2也落在直线y=- x上,如此下去……若点B的坐标为
(0,3),则点B37的坐标为( C )
A. (180,135) B. (180,133)
C. (-180,135) D. (-180,133)
C
8. [2024·广安]已知,直线l:y= x- 与x轴相交于点A1,以OA1为
边作等边三角形OA1B1,点B1在第一象限内,过点B1作x轴的平行线与
直线l交于点A2,与y轴交于点C1,以C1A2为边作等边三角形C1A2B2
(点B2在点B1的上方),以同样的方式依次作等边三角形C2A3B3,等
边三角形C3A4B4……则点A2 024的横坐标为 .
谢谢观看
同课章节目录
