中考数学几何模型决胜88招模型49 直角三角形之共斜边中点模型(含解析)
文档属性
| 名称 | 中考数学几何模型决胜88招模型49 直角三角形之共斜边中点模型(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 146.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-22 21:15:02 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
模型49 直角三角形之共斜边中点模型
跟踪练习
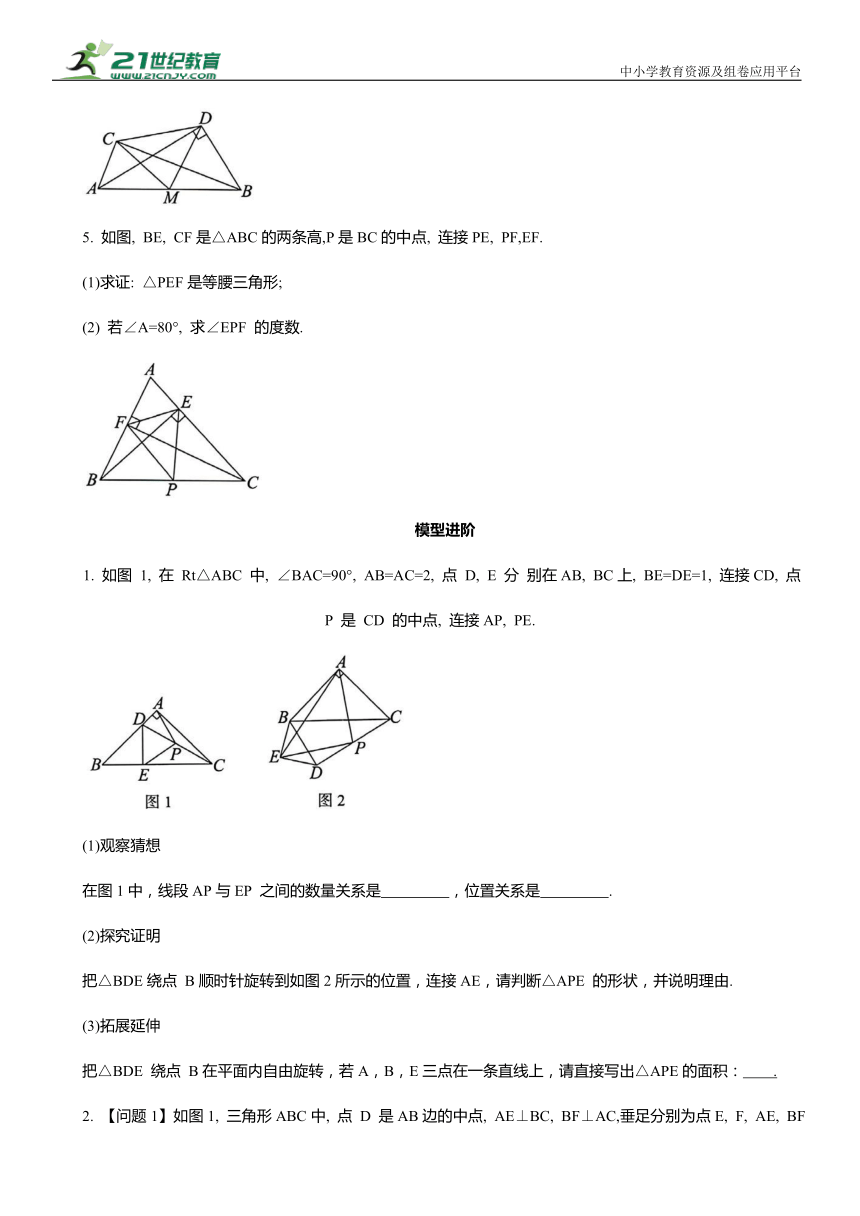
1. 如图所示, 在四边形ABCD中,∠BCD=90°, AB⊥BD 于点 B, 点 E是BD的中点, 连接AE, CE, 则AE与 CE 的大小关系是 ( )
A. AEC. AE>CE D. AE=2CE
2. 如图,在△ABC中,CD⊥AB于点D,BE⊥AC于点 E, F为BC的中点,DE=5, BC=10, 则△DEF 的 周长为 ( )
A.21 B.18 C.15 D.13
3. 如图,∠ABC=∠ADC=90°,∠BAD=70°, 点E是AC的中点, 则∠EBD的度数为 ( )
A.20° B.35° C.40° D.55°
4.如图,在直角三角形ABC和直角三角 形 ABD 中, ∠ACB=∠ADB=90°, AB=10, M是AB 的中点,连接MC, MD, CD, 若CD=6,则三角形 MCD的面积为 .
5. 如图, BE, CF是△ABC的两条高,P是BC的中点, 连接PE, PF,EF.
(1)求证: △PEF是等腰三角形;
(2) 若∠A=80°, 求∠EPF 的度数.
模型进阶
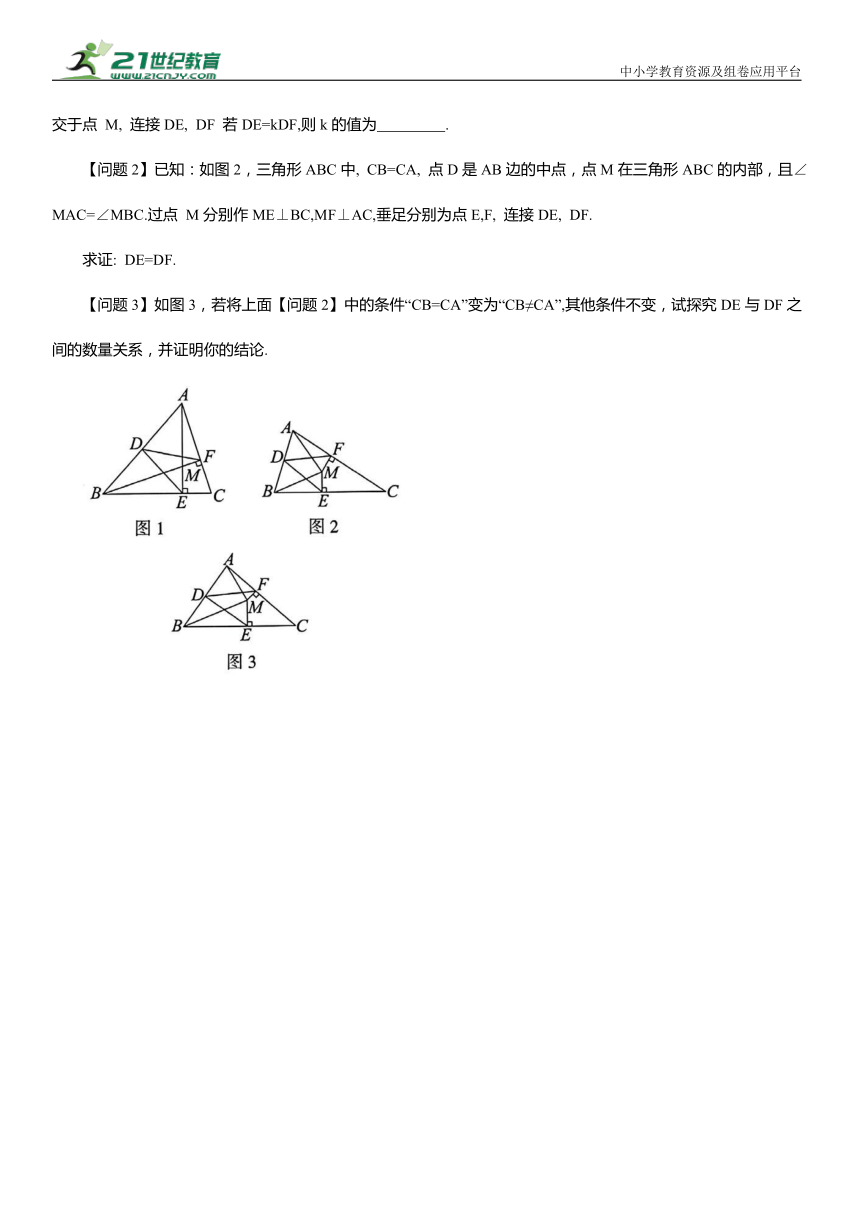
1. 如图 1, 在 Rt△ABC 中, ∠BAC=90°, AB=AC=2, 点 D, E 分 别在AB, BC上, BE=DE=1, 连接CD, 点 P 是 CD 的中点, 连接AP, PE.
(1)观察猜想
在图1中,线段AP与EP 之间的数量关系是 ,位置关系是 .
(2)探究证明
把△BDE绕点 B顺时针旋转到如图2所示的位置,连接AE,请判断△APE 的形状,并说明理由.
(3)拓展延伸
把△BDE 绕点 B在平面内自由旋转,若A,B,E三点在一条直线上,请直接写出△APE的面积: .
2. 【问题1】如图1, 三角形ABC中, 点 D 是AB边的中点, AE⊥BC, BF⊥AC,垂足分别为点E, F, AE, BF交于点 M, 连接DE, DF 若DE=kDF,则k的值为 .
【问题2】已知:如图2,三角形ABC中, CB=CA, 点D是AB边的中点,点M在三角形ABC的内部,且∠MAC=∠MBC.过点 M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F, 连接DE, DF.
求证: DE=DF.
【问题3】如图3,若将上面【问题2】中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证明你的结论.
1. C 解析: ∵ ∠BCD=90°, 点 E 是 BD的中点, ∴ CE=BE=DE, ∵ AB⊥BD,∴ ∠ABE=90°, ∴ AE>BE, ∴ AE>CE.故选C.
2. C 解析: ∵ CD⊥AB, F为BC的中点, F为BC的中点, ∴△DEF的周长=DE+EF+DF=5+5+5=15. 故选C.
3. A 解析: 如图, 连接DE, ∵∠ABC=∠ADC=90°, 点E是AC的中点, ∴点A,B,C,D在以E为圆心,AC为直径的同一个圆上, ∵ ∠BAD=70°, ∴ ∠DEB= 故选 A.
4. 12 解析: 过点 M 作ME⊥CD, 垂足为E, ∵∠ACB=∠ADB=90°, AB=10, M是AB的中点, AB=5,∴CM=DM,∵ME⊥CD,∴CE=DE= 在 Rt△CEM 中, EM= 的面积
5. 解析: (1)证明: ∵ BE, CF是△ABC的两条高,
∴ ∠BFC=∠BEC=90°,
∵ P是 BC的中点,
∴ FP=EP,
∴△PEF 是等腰三角形.
(2) ∵∠A=80°,
∴ ∠ABC+∠ACB=180°-∠A=100°,
由(1)得FP=BP, EP=CP,
∴∠ABC=∠BFP, ∠ACB=∠CEP,
∴ ∠BFP+∠CEP=∠ABC+∠ACB=100°,
∴ ∠FPB+∠EPC=360°-(∠ABC+∠ACB+∠BFP+∠CEP)=160°,
∴ ∠EPF=180°-(∠FPB+∠EPC) =20°.
模型进阶
1. 解析: (1) AP=EP AP⊥EP 提示:
∵ ∠BAC=90°, AB=AC,
∴ ∠ABC=∠ACB=45°,
∵ BE=ED, ∴ ∠ABC=∠BDE=45°,
∴∠BED=90°, ∴ DE⊥BC,
∵∠DAC=90°, 点 P 是CD的中点,
∵ ∠DAC=∠DEC=90°, ∴ ∠ADE=135°,
∴ DP=AP=PC=PE,
∴∠PDE=∠PED, ∠PAD=∠PDA,
∴ ∠PED+∠PDE+∠PDA+∠PAD=2∠ADE=270°, ∴∠APE=360°-270°=90°,∴ AP⊥EP.
(2)△APE是等腰直角三角形,理由如下: 取BD的中点F, 连接EF, PF, 取BC的中点G, 连接AG, PG, 如图1.
∵ F为BD的中点, ∠BED=90°,
∴ BF=EF=DF,
同理可得AG=BG=CG.
∵P, F, G分别为CD, BD, BC的中点,
同理可得
∴ PG=BF=EF, PF=BG=AG,∠CGP=∠CBD=∠PFD.
∵ ∠AGC=∠EFD=90°,
∴∠AGC+∠CGP=∠EFD+∠PFD,
即∠AGP=∠PFE,
又∵AG=PF, PG=EF,
∴△EFP≌△PGA(SAS),
∴ EP=AP, ∠FEP=∠GPA.
∵∠EFD=90°,
∴ ∠FEP+∠DFP+∠EPF=90°,
∵ PG∥BD, ∴∠DFP=∠FPG,
∴ ∠FPG+∠EPF+∠GPA=90°,
∴∠EPA=90°, ∴EP⊥AP,
∴△APE为等腰直角三角形.
(3) 或 提示:如图2,当点E在AB的延长线上时,
∵AB=2, BE=1, ∴AE=2+1=3,易得△AEP为等腰直角三角形,∴△APE 的面积为
如图3, 当点E在线段AB上时,∵ AB=2, BE=1, ∴ AE=1,易得△AEP为等腰直角三角形,∴△APE的面积为 综上所述,△APE的面积为 或
直击中考
2. 解析: 【问题1】1
【问题2】证明:∵CB=CA,
∴∠CAB=∠CBA.
∵∠MAC=∠MBC,
∴ ∠CAB-∠MAC=∠CBA-∠MBC,
即∠MAB=∠MBA,
∴ MA=MB.
∵ ME⊥BC, MF⊥AC,
∴ ∠AFM=∠BEM=90°.
在△AFM与△BEM中,
∴△AFM≌△BEM,
∴AF=BE.
∵点D是AB边的中点,
∴ BD=AD.
在△BDE与△ADF中,
∴△BDE≌△ADF,
∴ DE=DF.
【问题3】DE=DF.证明如下:
如图, 分别取AM, BM的中点G, H, 连接DG, FG, DH, EH.
∵点D,G,H分别是AB,AM,BM的中点,
∴ DG∥BM, DH∥AM, 且
∴四边形DHMG 是平行四边形,
∴ ∠DHM=∠DGM,
∵ME⊥BC, MF⊥AC,
∴ ∠AFM=∠BEM=90°,
∴ FG=DH, DG=EH, ∠GAF=∠GFA,∠HBE=∠HEB,
∴ ∠FGM=2∠FAM, ∠EHM=2∠EBM,
又∵ ∠FAM=∠EBM,
∴ ∠FGM=∠EHM,
∴ ∠DGM+∠FGM=∠DHM+∠EHM, 即∠DGF=∠DHE.
在△EHD与△DGF中,
∴△EHD≌△DGF,
∴ DE=DF.
模型49 直角三角形之共斜边中点模型
跟踪练习
1. 如图所示, 在四边形ABCD中,∠BCD=90°, AB⊥BD 于点 B, 点 E是BD的中点, 连接AE, CE, 则AE与 CE 的大小关系是 ( )
A. AE
2. 如图,在△ABC中,CD⊥AB于点D,BE⊥AC于点 E, F为BC的中点,DE=5, BC=10, 则△DEF 的 周长为 ( )
A.21 B.18 C.15 D.13
3. 如图,∠ABC=∠ADC=90°,∠BAD=70°, 点E是AC的中点, 则∠EBD的度数为 ( )
A.20° B.35° C.40° D.55°
4.如图,在直角三角形ABC和直角三角 形 ABD 中, ∠ACB=∠ADB=90°, AB=10, M是AB 的中点,连接MC, MD, CD, 若CD=6,则三角形 MCD的面积为 .
5. 如图, BE, CF是△ABC的两条高,P是BC的中点, 连接PE, PF,EF.
(1)求证: △PEF是等腰三角形;
(2) 若∠A=80°, 求∠EPF 的度数.
模型进阶
1. 如图 1, 在 Rt△ABC 中, ∠BAC=90°, AB=AC=2, 点 D, E 分 别在AB, BC上, BE=DE=1, 连接CD, 点 P 是 CD 的中点, 连接AP, PE.
(1)观察猜想
在图1中,线段AP与EP 之间的数量关系是 ,位置关系是 .
(2)探究证明
把△BDE绕点 B顺时针旋转到如图2所示的位置,连接AE,请判断△APE 的形状,并说明理由.
(3)拓展延伸
把△BDE 绕点 B在平面内自由旋转,若A,B,E三点在一条直线上,请直接写出△APE的面积: .
2. 【问题1】如图1, 三角形ABC中, 点 D 是AB边的中点, AE⊥BC, BF⊥AC,垂足分别为点E, F, AE, BF交于点 M, 连接DE, DF 若DE=kDF,则k的值为 .
【问题2】已知:如图2,三角形ABC中, CB=CA, 点D是AB边的中点,点M在三角形ABC的内部,且∠MAC=∠MBC.过点 M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F, 连接DE, DF.
求证: DE=DF.
【问题3】如图3,若将上面【问题2】中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证明你的结论.
1. C 解析: ∵ ∠BCD=90°, 点 E 是 BD的中点, ∴ CE=BE=DE, ∵ AB⊥BD,∴ ∠ABE=90°, ∴ AE>BE, ∴ AE>CE.故选C.
2. C 解析: ∵ CD⊥AB, F为BC的中点, F为BC的中点, ∴△DEF的周长=DE+EF+DF=5+5+5=15. 故选C.
3. A 解析: 如图, 连接DE, ∵∠ABC=∠ADC=90°, 点E是AC的中点, ∴点A,B,C,D在以E为圆心,AC为直径的同一个圆上, ∵ ∠BAD=70°, ∴ ∠DEB= 故选 A.
4. 12 解析: 过点 M 作ME⊥CD, 垂足为E, ∵∠ACB=∠ADB=90°, AB=10, M是AB的中点, AB=5,∴CM=DM,∵ME⊥CD,∴CE=DE= 在 Rt△CEM 中, EM= 的面积
5. 解析: (1)证明: ∵ BE, CF是△ABC的两条高,
∴ ∠BFC=∠BEC=90°,
∵ P是 BC的中点,
∴ FP=EP,
∴△PEF 是等腰三角形.
(2) ∵∠A=80°,
∴ ∠ABC+∠ACB=180°-∠A=100°,
由(1)得FP=BP, EP=CP,
∴∠ABC=∠BFP, ∠ACB=∠CEP,
∴ ∠BFP+∠CEP=∠ABC+∠ACB=100°,
∴ ∠FPB+∠EPC=360°-(∠ABC+∠ACB+∠BFP+∠CEP)=160°,
∴ ∠EPF=180°-(∠FPB+∠EPC) =20°.
模型进阶
1. 解析: (1) AP=EP AP⊥EP 提示:
∵ ∠BAC=90°, AB=AC,
∴ ∠ABC=∠ACB=45°,
∵ BE=ED, ∴ ∠ABC=∠BDE=45°,
∴∠BED=90°, ∴ DE⊥BC,
∵∠DAC=90°, 点 P 是CD的中点,
∵ ∠DAC=∠DEC=90°, ∴ ∠ADE=135°,
∴ DP=AP=PC=PE,
∴∠PDE=∠PED, ∠PAD=∠PDA,
∴ ∠PED+∠PDE+∠PDA+∠PAD=2∠ADE=270°, ∴∠APE=360°-270°=90°,∴ AP⊥EP.
(2)△APE是等腰直角三角形,理由如下: 取BD的中点F, 连接EF, PF, 取BC的中点G, 连接AG, PG, 如图1.
∵ F为BD的中点, ∠BED=90°,
∴ BF=EF=DF,
同理可得AG=BG=CG.
∵P, F, G分别为CD, BD, BC的中点,
同理可得
∴ PG=BF=EF, PF=BG=AG,∠CGP=∠CBD=∠PFD.
∵ ∠AGC=∠EFD=90°,
∴∠AGC+∠CGP=∠EFD+∠PFD,
即∠AGP=∠PFE,
又∵AG=PF, PG=EF,
∴△EFP≌△PGA(SAS),
∴ EP=AP, ∠FEP=∠GPA.
∵∠EFD=90°,
∴ ∠FEP+∠DFP+∠EPF=90°,
∵ PG∥BD, ∴∠DFP=∠FPG,
∴ ∠FPG+∠EPF+∠GPA=90°,
∴∠EPA=90°, ∴EP⊥AP,
∴△APE为等腰直角三角形.
(3) 或 提示:如图2,当点E在AB的延长线上时,
∵AB=2, BE=1, ∴AE=2+1=3,易得△AEP为等腰直角三角形,∴△APE 的面积为
如图3, 当点E在线段AB上时,∵ AB=2, BE=1, ∴ AE=1,易得△AEP为等腰直角三角形,∴△APE的面积为 综上所述,△APE的面积为 或
直击中考
2. 解析: 【问题1】1
【问题2】证明:∵CB=CA,
∴∠CAB=∠CBA.
∵∠MAC=∠MBC,
∴ ∠CAB-∠MAC=∠CBA-∠MBC,
即∠MAB=∠MBA,
∴ MA=MB.
∵ ME⊥BC, MF⊥AC,
∴ ∠AFM=∠BEM=90°.
在△AFM与△BEM中,
∴△AFM≌△BEM,
∴AF=BE.
∵点D是AB边的中点,
∴ BD=AD.
在△BDE与△ADF中,
∴△BDE≌△ADF,
∴ DE=DF.
【问题3】DE=DF.证明如下:
如图, 分别取AM, BM的中点G, H, 连接DG, FG, DH, EH.
∵点D,G,H分别是AB,AM,BM的中点,
∴ DG∥BM, DH∥AM, 且
∴四边形DHMG 是平行四边形,
∴ ∠DHM=∠DGM,
∵ME⊥BC, MF⊥AC,
∴ ∠AFM=∠BEM=90°,
∴ FG=DH, DG=EH, ∠GAF=∠GFA,∠HBE=∠HEB,
∴ ∠FGM=2∠FAM, ∠EHM=2∠EBM,
又∵ ∠FAM=∠EBM,
∴ ∠FGM=∠EHM,
∴ ∠DGM+∠FGM=∠DHM+∠EHM, 即∠DGF=∠DHE.
在△EHD与△DGF中,
∴△EHD≌△DGF,
∴ DE=DF.
同课章节目录
