中考数学几何模型决胜88招模型52 正方形之内十字模型(含解析)
文档属性
| 名称 | 中考数学几何模型决胜88招模型52 正方形之内十字模型(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 87.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-22 21:20:03 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
模型52 正方形之内十字模型
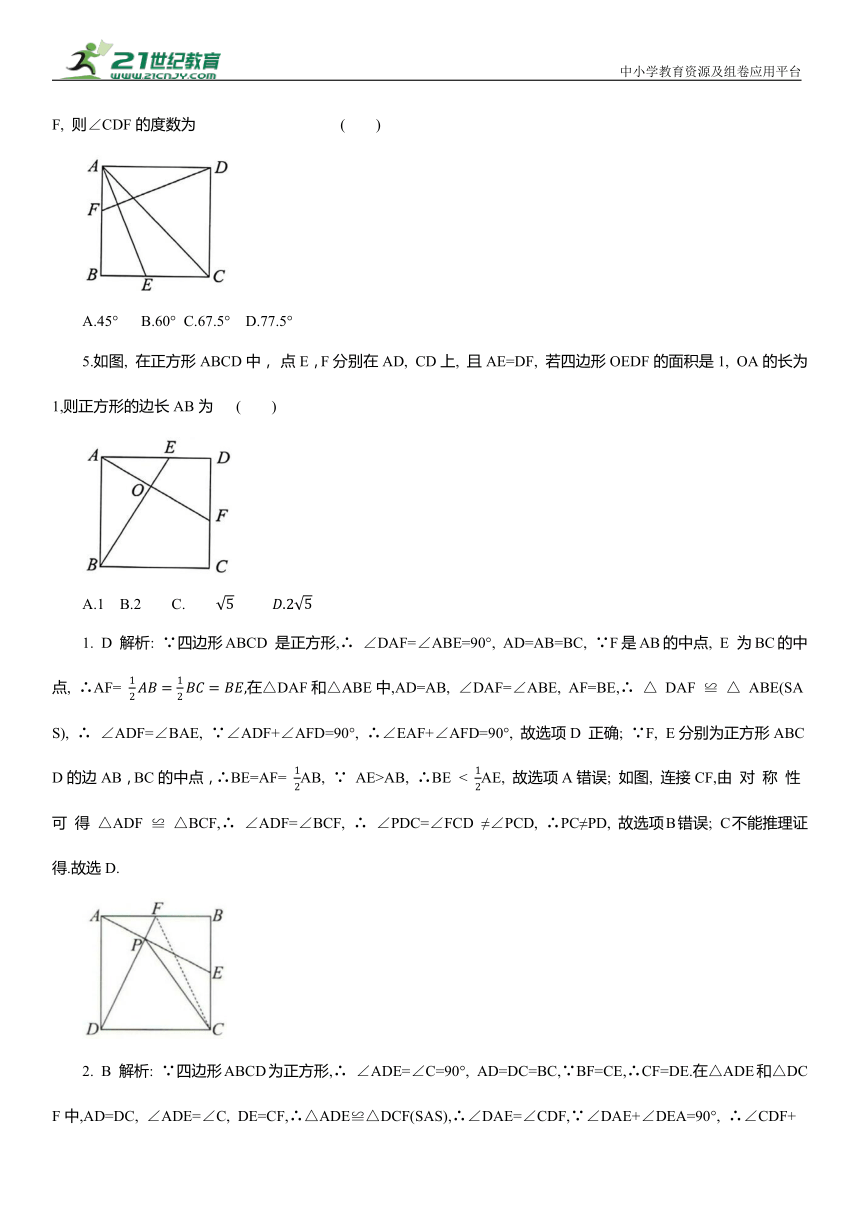
1.如图,已知 F,E分别是正方形ABCD的边AB, BC的中点, AE与DF交于P,则下列结论成立的是 ()
B. PC=PD
C. PE=PC D.∠EAF+∠AFD=90°
2. 如图,正方形ABCD的边长为6,点E,F分别在DC, BC上, BF=CE=4,连接AE, DF, AE与DF相交于点G, 连接AF, 取AF的中点 H, 连接HG, 则 HG的长为 ( )
A. C.5
3. 如图, 正方形ABCD的边长为10, E为AD的中点,连接CE,过点B作BF⊥CE交CD于点F, 垂足为G, 连接AG, DG, 给出下列结论: ①BF=CE; ②AG=CD; ③∠CDG=∠AGE;④EG=2 ⑤DG= CG. 其中正确的结论有 ( )
A.①②④ B.②③⑤
C.①②⑤ D.①④⑤
4. 如图, 在正方形ABCD 中, AE 平 分 ∠BAC 交 BC于点 E, 点F是边AB上一点, 连接DF, 若BE=AF, 则∠CDF的度数为 ( )
A.45° B.60° C.67.5° D.77.5°
5.如图, 在正方形ABCD中, 点E,F分别在AD, CD上, 且AE=DF, 若四边形OEDF的面积是1, OA的长为1,则正方形的边长AB为 ( )
A.1 B.2 C.
1. D 解析: ∵四边形ABCD 是正方形,∴ ∠DAF=∠ABE=90°, AD=AB=BC, ∵F是AB的中点, E 为BC的中点, ∴AF= 在△DAF和△ABE中,AD=AB, ∠DAF=∠ABE, AF=BE,∴ △ DAF ≌ △ ABE(SAS), ∴ ∠ADF=∠BAE, ∵∠ADF+∠AFD=90°, ∴∠EAF+∠AFD=90°, 故选项D 正确; ∵F, E分别为正方形ABCD的边AB,BC的中点,∴BE=AF= AB, ∵ AE>AB, ∴BE < AE, 故选项A错误; 如图, 连接CF,由 对 称 性 可 得 △ADF ≌ △BCF,∴ ∠ADF=∠BCF, ∴ ∠PDC=∠FCD ≠∠PCD, ∴PC≠PD, 故选项B错误; C不能推理证得.故选D.
2. B 解析: ∵四边形ABCD为正方形,∴ ∠ADE=∠C=90°, AD=DC=BC,∵BF=CE,∴CF=DE.在△ADE和△DCF中,AD=DC, ∠ADE=∠C, DE=CF,∴△ADE≌△DCF(SAS),∴∠DAE=∠CDF,∵∠DAE+∠DEA=90°, ∴∠CDF+∠DEA=90°, ∴∠AGF=∠DGE=90°, ∵点 H为AF的中点, 故选B.
3. C 解析: ∵四边形ABCD是正方形,∴ AD=CD=BC, ∠BCD=∠ADC=90°,∴ ∠DCE+∠DEC=90°, ∵BF⊥CE,∴ ∠DCE+ ∠BFC=90°, ∴∠BFC=∠DEC, ∴ △BFC≌ △CED(AAS),∴ BF=CE, 故①正确; 如图, 延长GE, BA, 交于点H, 过点D作DN⊥EC于 点 N, ∵ 点 E 是 AD 的 中 点,∴ AE=DE=5, ∵AB ∥CD, ∴ ∠H=∠DCE,又∵∠AEH=∠DEC, ∴△DEC≌△AEH(AAS), ∴ CD=AH, ∴ AB=AH,又 ∵ BF⊥CE, ∴ AG=AB=AH, ∴ AG=CD, 故②正确; ∵△BFC≌△CED,∴ DE= CF=5, CE=BF, ∴ BF= 故④错误; ∵ CG≠EG, ∴ 点G不是EC的中点,∴DG≠CG,∴∠GDC≠∠GCD,∵AG=AH,∴∠AGE=∠H,∴∠AGE=∠H=∠GCD≠∠GDC, 故③错误; 故⑤正确.综上, 正确的结论有①②⑤.故选C.
C 解析: ∵四边形ABCD是正方形,∴ AD=BA, ∠DAF=∠ABE=90°. 在△DAF 和△ABE 中, AD=BA, ∠DAF=∠ABE,AF=BE,∴△DAF≌△ABE(SAS),∴ ∠ADF=∠BAE. ∵ AE平分∠BAC, 四边 形 ABCD 是 正 方 形, ∴ ∠BAE= ∠BAC=22.5°, ∴ ∠ADF=22.5°,∵ ∠ADC= 90°, ∴ ∠CDF=∠ADC-∠ADF=90°-22.5°=67.5°.故选C.
5. C 解析: ∵四边形ABCD是正方形,∴ AB=AD,∠BAE=∠ADF=90°, 在△ABE和△DAF中, AB=AD, ∠BAE=∠ADF,AE=DF, ∴ △ABE ≌ △DAF(SAS),∴∠ABE=∠DAF,∴∠ABE+∠BAO=∠DAF+∠BAO=90°, ∴ ∠AOB=90°. ∵△ABE≌ 即 ∵OA=1,∴BO=2,∴AB=√AO +BO = 故选C.
模型52 正方形之内十字模型
1.如图,已知 F,E分别是正方形ABCD的边AB, BC的中点, AE与DF交于P,则下列结论成立的是 ()
B. PC=PD
C. PE=PC D.∠EAF+∠AFD=90°
2. 如图,正方形ABCD的边长为6,点E,F分别在DC, BC上, BF=CE=4,连接AE, DF, AE与DF相交于点G, 连接AF, 取AF的中点 H, 连接HG, 则 HG的长为 ( )
A. C.5
3. 如图, 正方形ABCD的边长为10, E为AD的中点,连接CE,过点B作BF⊥CE交CD于点F, 垂足为G, 连接AG, DG, 给出下列结论: ①BF=CE; ②AG=CD; ③∠CDG=∠AGE;④EG=2 ⑤DG= CG. 其中正确的结论有 ( )
A.①②④ B.②③⑤
C.①②⑤ D.①④⑤
4. 如图, 在正方形ABCD 中, AE 平 分 ∠BAC 交 BC于点 E, 点F是边AB上一点, 连接DF, 若BE=AF, 则∠CDF的度数为 ( )
A.45° B.60° C.67.5° D.77.5°
5.如图, 在正方形ABCD中, 点E,F分别在AD, CD上, 且AE=DF, 若四边形OEDF的面积是1, OA的长为1,则正方形的边长AB为 ( )
A.1 B.2 C.
1. D 解析: ∵四边形ABCD 是正方形,∴ ∠DAF=∠ABE=90°, AD=AB=BC, ∵F是AB的中点, E 为BC的中点, ∴AF= 在△DAF和△ABE中,AD=AB, ∠DAF=∠ABE, AF=BE,∴ △ DAF ≌ △ ABE(SAS), ∴ ∠ADF=∠BAE, ∵∠ADF+∠AFD=90°, ∴∠EAF+∠AFD=90°, 故选项D 正确; ∵F, E分别为正方形ABCD的边AB,BC的中点,∴BE=AF= AB, ∵ AE>AB, ∴BE < AE, 故选项A错误; 如图, 连接CF,由 对 称 性 可 得 △ADF ≌ △BCF,∴ ∠ADF=∠BCF, ∴ ∠PDC=∠FCD ≠∠PCD, ∴PC≠PD, 故选项B错误; C不能推理证得.故选D.
2. B 解析: ∵四边形ABCD为正方形,∴ ∠ADE=∠C=90°, AD=DC=BC,∵BF=CE,∴CF=DE.在△ADE和△DCF中,AD=DC, ∠ADE=∠C, DE=CF,∴△ADE≌△DCF(SAS),∴∠DAE=∠CDF,∵∠DAE+∠DEA=90°, ∴∠CDF+∠DEA=90°, ∴∠AGF=∠DGE=90°, ∵点 H为AF的中点, 故选B.
3. C 解析: ∵四边形ABCD是正方形,∴ AD=CD=BC, ∠BCD=∠ADC=90°,∴ ∠DCE+∠DEC=90°, ∵BF⊥CE,∴ ∠DCE+ ∠BFC=90°, ∴∠BFC=∠DEC, ∴ △BFC≌ △CED(AAS),∴ BF=CE, 故①正确; 如图, 延长GE, BA, 交于点H, 过点D作DN⊥EC于 点 N, ∵ 点 E 是 AD 的 中 点,∴ AE=DE=5, ∵AB ∥CD, ∴ ∠H=∠DCE,又∵∠AEH=∠DEC, ∴△DEC≌△AEH(AAS), ∴ CD=AH, ∴ AB=AH,又 ∵ BF⊥CE, ∴ AG=AB=AH, ∴ AG=CD, 故②正确; ∵△BFC≌△CED,∴ DE= CF=5, CE=BF, ∴ BF= 故④错误; ∵ CG≠EG, ∴ 点G不是EC的中点,∴DG≠CG,∴∠GDC≠∠GCD,∵AG=AH,∴∠AGE=∠H,∴∠AGE=∠H=∠GCD≠∠GDC, 故③错误; 故⑤正确.综上, 正确的结论有①②⑤.故选C.
C 解析: ∵四边形ABCD是正方形,∴ AD=BA, ∠DAF=∠ABE=90°. 在△DAF 和△ABE 中, AD=BA, ∠DAF=∠ABE,AF=BE,∴△DAF≌△ABE(SAS),∴ ∠ADF=∠BAE. ∵ AE平分∠BAC, 四边 形 ABCD 是 正 方 形, ∴ ∠BAE= ∠BAC=22.5°, ∴ ∠ADF=22.5°,∵ ∠ADC= 90°, ∴ ∠CDF=∠ADC-∠ADF=90°-22.5°=67.5°.故选C.
5. C 解析: ∵四边形ABCD是正方形,∴ AB=AD,∠BAE=∠ADF=90°, 在△ABE和△DAF中, AB=AD, ∠BAE=∠ADF,AE=DF, ∴ △ABE ≌ △DAF(SAS),∴∠ABE=∠DAF,∴∠ABE+∠BAO=∠DAF+∠BAO=90°, ∴ ∠AOB=90°. ∵△ABE≌ 即 ∵OA=1,∴BO=2,∴AB=√AO +BO = 故选C.
同课章节目录
